Икосаэдр


В геометрии икосаэдр ( / ˌ aɪ k ɒ s ə ˈ h iː d r ən , -k ə - , - koʊ / - or / aɪ ˌ k ɒ s ə ˈ h iː d r ən / [1] ) представляет собой многогранник с 20 гранями. Название происходит от древнегреческого εἴκοσι (eikosi) «двадцать» и ἕδρα (hédra) «сидение». Множественное число может быть либо «икосаэдры» ( /- d r ə / ), либо «икосаэдры».
Существует бесконечно много непохожих форм икосаэдров, причем некоторые из них более симметричны, чем другие. Самым известным является ( выпуклый , незвездчатый ) правильный икосаэдр — одно из платоновых тел , грани которого представляют собой 20 равносторонних треугольников .
Правильные икосаэдры
Есть два объекта, выпуклый и невыпуклый, которые оба можно назвать правильными икосаэдрами. Каждый из них имеет 30 ребер и 20 граней равностороннего треугольника , по пять сходящихся в каждой из двенадцати вершин. Оба имеют икосаэдрическую симметрию . Термин «правильный икосаэдр» обычно относится к выпуклой разновидности, тогда как невыпуклая форма называется большим икосаэдром .
Выпуклый правильный икосаэдр

Выпуклый правильный икосаэдр обычно называют просто правильным икосаэдром , одним из пяти правильных платоновых тел , и он представлен символом Шлефли {3, 5}, содержащим 20 треугольных граней, по 5 граней, встречающихся вокруг каждой вершины.
Его двойственный многогранник представляет собой правильный додекаэдр {5, 3}, имеющий три правильные пятиугольные грани вокруг каждой вершины.
Большой икосаэдр

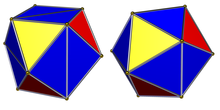
Большой икосаэдр — один из четырех правильных звездных многогранников Кеплера-Пуансо . Его символ Шлефли — {3, 5/2 } . Как и выпуклая форма, она также имеет 20 равносторонних треугольных граней, но фигура ее вершины представляет собой пентаграмму, а не пятиугольник, что приводит к геометрически пересекающимся граням. Пересечения треугольников не представляют собой новые ребра.
Его двойственный многогранник — это большой звездчатый додекаэдр { 5 / 2 , 3}, имеющий три правильные пятиугольные грани звезды вокруг каждой вершины.
Звездчатые икосаэдры
Звездчатость — это процесс удлинения граней или ребер многогранника до тех пор, пока они не встретятся и не образуют новый многогранник. Это делается симметрично, чтобы полученная фигура сохранила общую симметрию родительской фигуры.
В своей книге «Пятьдесят девять икосаэдров » Коксетер и др. насчитал 58 таких звездочек правильного икосаэдра.
Многие из них имеют по одной грани в каждой из 20 плоскостей граней и поэтому также являются икосаэдрами. Среди них – великий икосаэдр.
Другие звездчатые имеют более одной грани в каждой плоскости или образуют соединения более простых многогранников. Это не строго икосаэдры, хотя их часто называют таковыми.
| Известные звездочки икосаэдра | |||||||||
| Обычный | Униформа двойная | Регулярные соединения | Обычная звезда | Другие | |||||
| (Выпуклый) икосаэдр | Малый триамбический икосаэдр | Медиальный триамбический икосаэдр | Большой триамбический икосаэдр | Соединение пяти октаэдров | Соединение пяти тетраэдров | Соединение десяти тетраэдров | Большой икосаэдр | Раскопанный додекаэдр | Последняя звездочка |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией . | |||||||||
Пиритоэдрическая симметрия
| Пиритоэдрическая и тетраэдрическая симметрия | |||||
|---|---|---|---|---|---|
| Диаграммы Кокстера | |||||
| Символ Шлефли | с{3,4} ср{3,3} или | ||||
| Лица | 20 треугольников: 8 равносторонних 12 равнобедренных | ||||
| Края | 30 (6 коротких + 24 длинных) | ||||
| Вершины | 12 | ||||
| Группа симметрии | Т ч , [4,3 + ], (3*2), порядок 24 | ||||
| Группа вращения | Т д , [3,3] + , (332), порядок 12 | ||||
| Двойной многогранник | Пиритоэдр | ||||
| Характеристики | выпуклый | ||||
 Сеть | |||||
| |||||
может Правильный икосаэдр быть искажен или отмечен как более низкая пиритоэдрическая симметрия. [2] [3] и называется курносым октаэдром , курносым тетратетраэдром , курносым тетраэдром и псевдоикосаэдром . [4] Это можно рассматривать как чередующийся усеченный октаэдр . Если все треугольники равносторонние , симметрию можно также отличить, раскрасив наборы треугольников 8 и 12 по-разному.
Пиритоэдрическая симметрия имеет обозначение (3*2), [3 + ,4], порядка 24. Тетраэдрическая симметрия имеет символ (332), [3,3] + , с порядком 12. Эти более низкие симметрии допускают геометрические искажения из-за 20 равносторонних треугольных граней вместо 8 равносторонних треугольников и 12 конгруэнтных равнобедренных треугольников .
Эти симметрии предлагают диаграммы Кокстера : ![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]()
![]()
![]() соответственно, каждый из которых представляет более низкую симметрию правильного икосаэдра.
соответственно, каждый из которых представляет более низкую симметрию правильного икосаэдра. ![]()
![]()
![]()
![]()
![]() , (*532), [5,3] икосаэдрическая симметрия порядка 120.
, (*532), [5,3] икосаэдрическая симметрия порядка 120.
Декартовы координаты

Координаты 12 вершин могут быть определены векторами, определяемыми всеми возможными циклическими перестановками и сменами знаков координат формы (2, 1, 0). Эти координаты [ сломанный якорь ] представляют собой усеченный октаэдр с удаленными чередующимися вершинами.
Эта конструкция называется курносым тетраэдром в его правильной форме икосаэдра, порожденной теми же операциями, выполняемыми, начиная с вектора ( φ , 1, 0), где φ — золотое сечение . [3]
Икосаэдр Джессена

В икосаэдре Йессена, иногда называемом ортогональным икосаэдром Йессена , 12 равнобедренных граней расположены по-разному, так что фигура невыпуклая и имеет прямые двугранные углы .
Это ножницы, конгруэнтные кубу, а это означает, что его можно разрезать на более мелкие многогранные части, которые можно переставлять, образуя сплошной куб.
Кубооктаэдр

Правильный икосаэдр топологически идентичен кубооктаэдру с шестью квадратными гранями, разделенными пополам по диагоналям с пиритоэдрической симметрией. Икосаэдры с пиритоэдрической симметрией составляют бесконечное семейство многогранников, в которое входят кубооктаэдр, правильный икосаэдр, икосаэдр Джессена и октаэдр с двойным покрытием . Между членами этого семейства существуют циклические кинематические преобразования.
Другие икосаэдры

Ромбический икосаэдр
Ромбический икосаэдр представляет собой зоноэдр, состоящий из 20 равных ромбов. Его можно получить из ромботриаконтаэдра , удалив 10 средних граней. Несмотря на то, что все грани конгруэнтны, ромбический икосаэдр не является транзитивным по граням .
Симметрии пирамид и призм
Общие икосаэдры с симметрией пирамиды и призмы включают:
- 19-гранная пирамида (плюс 1 основание = 20).
- 18-гранная призма (плюс 2 конца = 20).
- 9-сторонняя антипризма (2 набора по 9 сторон + 2 конца = 20).
- 10-сторонняя бипирамида (2 набора по 10 сторон = 20).
- 10-гранный трапецоэдр (2 набора по 10 сторон = 20).
Твердые вещества Джонсона
Некоторые тела Джонсона являются икосаэдрами: [5]
| J22 | J35 | J36 | J59 | J60 | J92 |
|---|---|---|---|---|---|
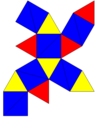
 Гироудлиненный треугольный купол |  Удлиненный треугольный ортобикупол. |  Гиробикупол вытянутой треугольной формы. |  Парабиаугментированный додекаэдр |  Метабиаугментированный додекаэдр |  Треугольная гебесфеноротонда |
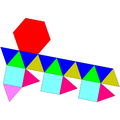 |  | 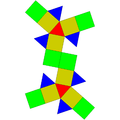 |  |  | 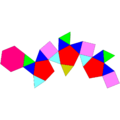 |
| 16 треугольников 3 квадрата 1 шестиугольник | 8 треугольников 12 квадратов | 8 треугольников 12 квадратов | 10 треугольников 10 пятиугольников | 10 треугольников 10 пятиугольников | 13 треугольников 3 квадрата 3 пятиугольника 1 шестиугольник |
См. также
Ссылки
- ^ Джонс, Дэниел (2003) [1917], Питер Роуч; Джеймс Хартманн; Джейн Сеттер (ред.), Словарь английского произношения , Кембридж: Издательство Кембриджского университета, ISBN 3-12-539683-2
- ^ Коджа, Назифе; Аль-Мухаини, Аида; Коджа, Мехмет; Аль Каноби, Амаль (1 декабря 2016 г.). «Симметрия пиритоэдра и решеток» . Научный журнал Университета Султана Кабуса [SQUJS] . 21 (2): 139. doi : 10.24200/squjs.vol21iss2pp139-149 .
- ^ Перейти обратно: а б Джон Баэз (11 сентября 2011 г.). «Золото дураков» .
- ^ Каппрафф, Джей (1991). Связи: Геометрический мост между искусством и наукой (2-е изд.). Всемирная научная. п. 475.
- ^ Икосаэдр в Mathworld.