Соединение пяти тетраэдров
| Соединение пяти тетраэдров | |
|---|---|
 | |
| Тип | Обычное соединение |
| Символ Коксетера | {5,3}[5{3,3}] {3,5} [1] |
| Индекс | УК 5 , Вт 24 |
| Элементы (В виде соединения) | 5 тетраэдров : Ф = 20, Е = 30, В = 20 |
| Двойное соединение | Самодвойственный |
| Группа симметрии | хиральный икосаэдр ( I ) |
| Подгруппа, ограничивающаяся одним компонентом | хиральный тетраэдр ( T ) |

Соединение — одно из пяти тетраэдров пяти правильных многогранников. Этот составной многогранник также является звездчатой формой правильного икосаэдра . Впервые он был описан Эдмундом Гессом в 1876 году.
Его можно рассматривать как огранку правильного додекаэдра .
В качестве соединения [ править ]
Его можно построить, расположив пять тетраэдров с вращательной икосаэдрической симметрией ( I ), как показано в верхней правой модели. Это одно из пяти правильных соединений , которые могут быть построены из идентичных платоновых тел . [2]
Он имеет то же расположение вершин, что и обычный додекаэдр .
Существуют две энантиоморфные формы (одна и та же фигура, но противоположной киральности) этого составного многогранника. Обе формы вместе создают зеркально-симметричное соединение десяти тетраэдров .
Имеет плотность выше 1.
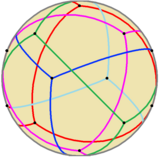 В виде сферической плитки |  Прозрачные модели (Анимация) |  Пять переплетенных тетраэдров |
Как созвездие [ править ]
Его также можно получить путем звездообразования икосаэдра , и он обозначается как индекс модели Веннингера 24 . [3]
| Звездчатая диаграмма | звездообразования Ядро | Выпуклая оболочка |
|---|---|---|
 | 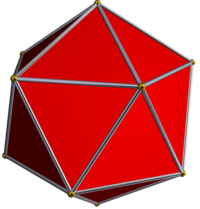 Икосаэдр | 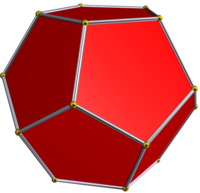 Додекаэдр |
В качестве огранки [ править ]

Это огранка додекаэдра, как показано слева.
Теория групп [ править ]
Соединение пяти тетраэдров является геометрической иллюстрацией понятия орбит и стабилизаторов следующим образом.
Группой симметрии соединения является (вращательная) икосаэдрическая группа I порядка 60, тогда как стабилизатором отдельного выбранного тетраэдра является (вращательная) тетраэдрическая группа T порядка 12, а пространство орбит I / T (порядка 60/ 12 = 5) естественным образом отождествляется с 5-тетраэдрами – смежный класс gT соответствует тому, в какой тетраэдр g отправляет выбранный тетраэдр.
Необычное двойное свойство [ править ]

Это соединение необычно тем, что двойная фигура является энантиоморфом оригинала. Если грани скручены вправо, то вершины скручены влево. Когда мы дуализируем , грани дуализируются в вершины, скрученные вправо, а вершины дуализируются в грани, скрученные влево, давая киральный двойник. Фигурки с таким свойством встречаются крайне редко.
В 4-х мерном пространстве [ править ]
Соединение пяти тетраэдров родственно правильному 5-клеточному , 4-симплексному правильному 4-многограннику , который также составлен из 5 правильных тетраэдров. В 5-ячейке тетраэдры соединены лицом к лицу так, что каждая треугольная грань является общей для двух тетраэдрических ячеек.
Соединение пяти тетраэдров возникает в 4-мерном пространстве , вписанном в 120 додекаэдрических ячеек 120-ячейки . 120-ячеечный — самый большой и полный правильный 4-мерный многогранник ; Обычный 5-элементный — самый маленький и простой. 120-ячейка содержит вписанные в себя экземпляры всех остальных правильных 4-многогранников. [4] В каждую из 120-ячеечных додекаэдрических ячеек имеется два вписанных экземпляра соединения пяти тетраэдров (другими словами, один экземпляр соединения десяти тетраэдров ). 5 тетраэдров каждого соединения из пяти встречаются как ячейки другого правильного 4-многогранника, вписанного в 120-ячеечный, 600-ячеечный , который имеет в качестве ячеек 600 правильных тетраэдров. 120-ячейка представляет собой соединение 5 непересекающихся 600-ячеек, а каждая из ее додекаэдрических ячеек представляет собой соединение 5 тетраэдрических ячеек , по одной ячейке от каждой из 5 непересекающихся 600-ячеек.
См. также [ править ]
Цитаты [ править ]
- ^ Коксетер 1973 , с. 98.
- ^ Coxeter 1973 , стр. 47–50, §3.6 Пять правильных соединений.
- ^ Коксетер 1973 , стр. 96–104, §6.2 Стулирование платоновых тел.
- ^ Коксетер 1973 , с. 269, Соединения; «Примечательно, что вершины {5, 3, 3} включают вершины всех остальных пятнадцати правильных многогранников в четырех измерениях».
Ссылки [ править ]
- Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN 0-521-09859-9 .
- Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
- Коксетер, Гарольд Скотт Макдональд ; Дю Валь, П.; Флатер, ХТ; Петри, Дж. Ф. (1999) [1938]. Пятьдесят девять икосаэдров (3-е изд.). Тарквиний. ISBN 978-1-899618-32-3 . МР 0676126 .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «5-соединение тетраэдра» . Математический мир .
- Металлическая скульптура соединения пяти тетраэдров
- Модель VRML : [1]
- Соединения тетраэдров 5 и 10, автор Шандор Кабай, Демонстрационный проект Вольфрама .
- Клитцинг, Ричард. «3D соединение» .
| Известные звездочки икосаэдра | |||||||||
| Обычный | Униформа двойная | Регулярные соединения | Обычная звезда | Другие | |||||
| (Выпуклый) икосаэдр | Малый триамбический икосаэдр | Медиальный триамбический икосаэдр | Большой триамбический икосаэдр | Соединение пяти октаэдров | Соединение пяти тетраэдров | Соединение десяти тетраэдров | Большой икосаэдр | Раскопанный додекаэдр | Последняя звездочка |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией . | |||||||||