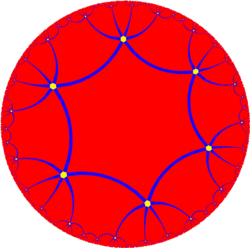
Раскопанный додекаэдр

Раскопанный додекаэдр
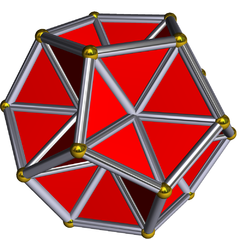(см. 3D модель )
Тип	Звездчатость
Индекс	Вт 28 , 26/59
Элементы (Как звездчатый многогранник)	Ф = 20, Е = 60 V = 20 ( χ = −20)
Лица	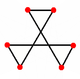Звездный шестиугольник
Вершинная фигура	Вогнутый шестиугольник
Звездчатая диаграмма
Группа симметрии	икосаэдрический ( I h )
Двойной многогранник	себя
Характеристики	благородный многогранник , транзитивный вершинный многогранник , самодвойственный многогранник

В геометрии представляет раскопанный додекаэдр собой звездчатый многогранник , похожий на додекаэдр с вогнутыми пятиугольными пирамидами на месте граней. Его внешняя поверхность представляет собой Ef ₁ g ₁ звездчатку икосаэдра он появляется Магнуса Веннингера . В книге «Модели многогранников» как модель 28, третья звездчатка икосаэдра .

Описание

Все 20 вершин и 30 из 60 ребер принадлежат его додекаэдрической оболочке. Остальные 30 внутренних ребер длиннее и принадлежат большому звездчатому додекаэдру . (Каждая грань содержит одно из 30 ребер ядра икосаэдра .) Каждая грань представляет собой самопересекающийся шестиугольник с чередующимися длинными и короткими ребрами и углами 60°. Равносторонние треугольники, соприкасающиеся коротким краем, являются частью лица. (Меньший между длинными ребрами представляет собой грань ядра икосаэдра.)

Основной	Длинные края	Лица	Халл	Резать
Икосаэдр	Г. с. додекаэдр		Додекаэдр	одна шестиугольная грань синего цвета

Огранка додекаэдра

Он имеет ту же внешнюю форму, что и некоторая огранка додекаэдра , имеющая в качестве граней 20 самопересекающихся шестиугольников . Невыпуклую грань шестиугольника можно разбить на четыре равносторонних треугольника, три из которых имеют одинаковый размер. Истинный выкопанный додекаэдр имеет три конгруэнтных равносторонних треугольника как истинные грани многогранника, тогда как внутренний равносторонний треугольник отсутствует.

20 вершин выпуклой оболочки соответствуют вершин додекаэдра . расположению

• 
  Выделена одна из граней шестиугольника звезды.
• 
  Его грань как грань додекаэдра .

Огранка представляет собой благородный многогранник . Имея шесть шестисторонних граней вокруг каждой вершины, он топологически эквивалентен фактор-пространству гиперболической шестиугольной мозаики 6-го порядка , {6,6} и является абстрактным типом {6,6} ₆ . Это один из десяти абстрактных правильных многогранников индекса два с вершинами на одной орбите.

Связанные многогранники

Пентакисдодекаэдр (слева) с перевернутыми пирамидами (справа) имеет ту же поверхность , что и раскопанный додекаэдр.	Грани эда (слева) являются частью граней большого икосаэдра (справа). Удлинение коротких сторон шестиугольника до их встречи дает треугольник, в который он входит. Замена каждого самопересекающегося шестиугольника выпуклым дает фигуру, содержащую ребра соединения пяти кубов (средний). Но на самом деле это не многогранник, поскольку каждое из этих ребер принадлежит только одной грани.
Большой додекаэдр (слева) представляет собой раскопанный икосаэдр . Он также имеет 60 видимых треугольников. Но в отличие от эл. д. (справа) у него выпуклые грани и, следовательно, нет внутренних краев.

Ссылки

• HSM Coxeter , Правильные многогранники , (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8 , 3.6 6.2 Стулирование платоновых тел , стр. 96-104

Известные звездочки икосаэдра
Обычный	Униформа двойная			Регулярные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Последняя звездочка
Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией .