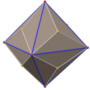
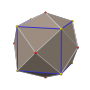
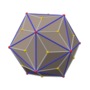
Додекаэдр Дисдякиса

Додекаэдр Дисдякиса
( вращающаяся и 3D- модель)
Тип	Каталонский солид
Обозначение Конвея	МК
Диаграмма Кокстера
Лицевой многоугольник	разносторонний треугольник
Лица	48
Края	72
Вершины	26 = 6 + 8 + 12
Конфигурация лица	Версия 4.6.8
Группа симметрии	О _ч , Б ₃ , [4,3], *432
Двугранный угол	155° 4 фута 56 дюймов $\arccos(-{\frac {71+12{\sqrt {2}}}{97}})$
Двойной многогранник	усеченный кубооктаэдр
Характеристики	выпуклый, гране-переходный
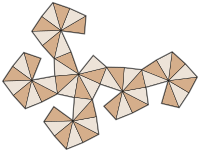сеть

В геометрии , додекаэдр Дисдякиса (также шестиоктаэдр , ^[1] шестигранник-октаэдр , октакис-куб , октакис-гексаэдр , кисромбический додекаэдр ^[2]), представляет собой каталонское тело с 48 гранями и двойственное архимедову усеченному кубооктаэдру . По существу, он транзитивен по граням , но имеет неправильные многоугольники граней. Он напоминает увеличенный ромбический додекаэдр . Замена каждой грани ромбододекаэдра плоской пирамидой создает многогранник, который выглядит почти как додекаэдр Дисдякиса и топологически эквивалентен ему.

Более формально, додекаэдр Дисдиакиса — это ромбододекаэдра и барицентрическое подразделение куба клитопа или правильного октаэдра . ^[3] Сеть ромбической додекаэдрической пирамиды также имеет ту же топологию.

Симметрия

Он обладает _{октаэдрической} симметрией . Его коллективные края представляют собой плоскости отражения симметрии. Его также можно увидеть в триангуляции угла и среднего ребра правильного куба и октаэдра, а также ромбододекаэдра.

Дисдякис додекаэдр	Дельтовидный икоситетраэдр	ромбический додекаэдр	Шестигранник	Октаэдр

Сферический многогранник

(see rotating model)	Orthographic projections from 2-, 3- and 4-fold axes

Ребра сферического додекаэдра Дисдякиса принадлежат 9 большим кругам . Три из них образуют сферический октаэдр (серый на изображениях ниже). Остальные шесть образуют три квадратных осоэдра (красный, зеленый и синий на изображениях ниже). Все они соответствуют зеркальным плоскостям — первые в диэдрической [2,2], а вторые в тетраэдрической [3,3] симметрии.

Стереографические проекции
	2-fold	3-fold	4-fold

Декартовы координаты

Позволять $~a={\frac {1}{1+2{\sqrt {2}}}}~{\color {Gray}\approx 0.261},~~b={\frac {1}{2+3{\sqrt {2}}}}~{\color {Gray}\approx 0.160},~~c={\frac {1}{3+3{\sqrt {2}}}}~{\color {Gray}\approx 0.138}$ .
Тогда декартовы координаты вершин додекаэдра Дисдиакиса с центром в начале координат:

● перестановки (± a , 0, 0) (вершины октаэдра)
● перестановки (± b , ± b , 0) (вершины кубооктаэдра )
● (± c , ± c , ± c ) (вершины куба)

Выпуклые оболочки
Combining an octahedron, cube, and cuboctahedron to form the disdyakis dodecahedron. The convex hulls for these vertices^[4] scaled by $1/a$ result in Cartesian coordinates of unit circumradius, which are visualized in the figure below:

Размеры

Если его наименьшие ребра имеют длину a , то площадь его поверхности и объем равны

{\begin{aligned}A&={\tfrac {6}{7}}{\sqrt {783+436{\sqrt {2}}}}\,a^{2}\\V&={\tfrac {1}{7}}{\sqrt {3\left(2194+1513{\sqrt {2}}\right)}}a^{3}\end{aligned}}

Лица представляют собой разносторонние треугольники. Их углы $\arccos {\biggl (}{\frac {1}{6}}-{\frac {1}{12}}{\sqrt {2}}{\biggr )}~{\color {Gray}\approx 87.201^{\circ }}$ , $\arccos {\biggl (}{\frac {3}{4}}-{\frac {1}{8}}{\sqrt {2}}{\biggr )}~{\color {Gray}\approx 55.024^{\circ }}$ и $\arccos {\biggl (}{\frac {1}{12}}+{\frac {1}{2}}{\sqrt {2}}{\biggr )}~{\color {Gray}\approx 37.773^{\circ }}$ .

Ортогональные проекции

Усеченный кубооктаэдр и его двойственный додекаэдр Дисдиакиса можно нарисовать в ряде симметричных ортогональных проективных ориентаций. Между многогранником и его двойником вершины и грани поменяны местами, а ребра перпендикулярны.

Проективный симметрия	[4]	[3]	[2]	[2]	[2]	[2]	[2] ⁺
Изображение
Двойной изображение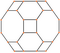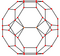

Связанные многогранники и мозаики


Многогранники, подобные додекаэдру Дисдякиса, являются двойственными октаэдру Боути и кубу , содержащим дополнительные пары треугольных граней. ^[5]

Додекаэдр Дисдиакиса — один из семейства двойственных однородным многогранникам, родственным кубу и правильному октаэдру.

Однородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Это многогранники в последовательности, определенной конфигурацией граней V4.6.2 n . Эта группа особенна тем, что имеет все четное количество ребер на вершину и образует биссектрисы, проходящие через многогранники и бесконечные прямые на плоскости, и продолжается в гиперболическую плоскость для любого n ≥ 7.

При четном количестве граней в каждой вершине эти многогранники и мозаики можно показать, чередуя два цвета, чтобы все соседние грани имели разные цвета.

Каждая грань в этих областях также соответствует фундаментальной области группы симметрии с порядками 2,3, n зеркалами в каждой вершине грани треугольника.

* n 32 мутация симметрии всеусеченных мозаик: 4.6.2n v т и
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

* n 42 мутация симметрии всеусеченных мозаик: 4.8.2n v т и
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

См. также

Первая звездчатая форма ромбододекаэдра.
Триаконтаэдр Дисдякиса
Плитка Кисромбилла
Большой ромбигексакрон — однородный двойной многогранник с одинаковой топологией поверхности.

Ссылки

^ «Ключевое слово: «формы» | ClipArt ETC» .
^ Конвей, Симметрии вещей, стр.284.
^ Лангер, Джоэл К.; Сингер, Дэвид А. (2010), «Размышления о лемнискате Бернулли: сорок восемь граней математической жемчужины», Milan Journal of Mathematics , 78 (2): 643–682, doi : 10.1007/s00032-010- 0124-5 , МР 2781856
^ Коджа, Мехмет; Оздеш Коджа, Назифе; Коч, Рамазон (2010). «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов». Журнал математической физики . 51 (4). arXiv : 0908.3272 . дои : 10.1063/1.3356985 .
^ Симметроэдры: многогранники из симметричного размещения правильных многоугольников Крейг С. Каплан

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 [1] (Глава 21, Названия архимедовых и каталанских многогранников и мозаик, страница 285, kisRhombic dodecahedron)

Внешние ссылки

Вайсштейн, Эрик В. , « Додекаэдр Дисдякиса » (« каталонское тело ») в MathWorld .
Додекаэдр Дисдякиса (Гексакис Октаэдр) Интерактивная модель многогранника

[1] «Ключевое слово: «формы» | ClipArt ETC» .

[2] Конвей, Симметрии вещей, стр.284.

[3] Лангер, Джоэл К.; Сингер, Дэвид А. (2010), «Размышления о лемнискате Бернулли: сорок восемь граней математической жемчужины», Milan Journal of Mathematics , 78 (2): 643–682, doi : 10.1007/s00032-010- 0124-5 , МР 2781856

[4] Коджа, Мехмет; Оздеш Коджа, Назифе; Коч, Рамазон (2010). «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов». Журнал математической физики . 51 (4). arXiv : 0908.3272 . дои : 10.1063/1.3356985 .

[5] Симметроэдры: многогранники из симметричного размещения правильных многоугольников Крейг С. Каплан

[1]

[2]

[3]

[4]

[5]