Пентадекаэдр
 | Вы можете помочь дополнить эту статью текстом, переведенным из соответствующей статьи на китайском языке . (Июнь 2023 г.) Нажмите [показать], чтобы просмотреть важные инструкции по переводу. |
| Некоторые пентадекаэдры | |
|---|---|
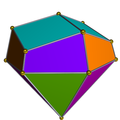 Двойная вытянутая треугольная главка |  Вытянутая пятиугольная дипирамида |
 Трехдесятиугольная призма |  Вытянутая семиугольная пирамида |
Пентадекаэдр пентакаидекаэдр (или многогранник ) — с 15 гранями . Ни один пентадекаэдр не является правильным ; следовательно, название неоднозначно. Существует множество топологически различных форм пентадекаэдра, например тетрадекагональная пирамида и тридекагональная призма . В пентадекаэдре ни одна из фигур не является правильным многогранником, иными словами, правильного пентадекаэдра не существует, и пентадекаэдр не может заполнить пространство, или не существует заполняющего пространство пентадекаэдра. [1]
В химии некоторые скопления атомов имеют форму пентадекаэдров. [2] Расчеты показали, что в кристалле существует устойчивая элементарная ячейка пентадекаэдра. [3]
Выпуклый
[ редактировать ]Существует 23 833 988 129 топологически различных выпуклых пентадекаэдров, исключая зеркальные изображения, имеющих не менее 10 вершин. [4] (Два многогранника «топологически различны», если они имеют существенно различное расположение граней и вершин, так что невозможно исказить один в другой, просто изменяя длины ребер или углы между ребрами или гранями.)
Обычные пентадекаэдры
[ редактировать ]| Имя | Тип | Изображение | Символ | Вершины | Стороны | Лица | час | Тип лица | Симметрия |
|---|---|---|---|---|---|---|---|---|---|
| Трехдесятиугольная призма | призма |  | т{2,13} {13}х{}      | 26 | 39 | 15 | 2 | 2 тридекагона 13 прямоугольников | Д 13h , [13,2], (*13 2 2) |
| Тетрадекагональная пирамида | пирамида |  | ( )∨{14} | 15 | 28 | 15 | 2 | 1 тетрадекагон 14 треугольников | С 14в , [14], (*14 14) |
| Вытянутая семиугольная пирамида | пирамида |  | 15 | 28 | 15 | 2 | 7 треугольников 7 прямоугольников 1 семиугольник | D 7h , [7,2], (*227), порядок 28 | |
| Семиугольный усеченный конус | усеченный конус |  | 15 | 28 | 15 | 2 | 7 треугольников 7 воздушных змеев 1 семиугольник | D 7h , [7,2], (*227), порядок 28 | |
| Вытянутая пятиугольная бипирамида | Бипирамида Джонсон твердый |  | 12 | 25 | 15 | 2 | 10 треугольников 5 квадратов | Д 5h , [5,2], (*225) |
Ссылки
[ редактировать ]- ^ Паркер, Мэтт (11 июня 2020 г.) Большие идеи в математике 2: От счета на пальцах до математической магии путешествия по четвёртому измерению Тайваня)). (на китайском языке ( ISBN 978-986-262-426-5 .
- ^ Монтехано, Х.М., Родригес, Х.Л., Гутьеррес-Винг, К., Мики, М. и Хосе-Якаман, М. (2004). «Кристаллография и форма наночастиц и кластеров» (PDF) . Энциклопедия нанонауки и нанотехнологий X : 1–44. Архивировано из оригинала (PDF) 28 августа 2022 г. Проверено 26 июня 2023 г.
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Лагунов В.А. и Синани А.Б. (1998). «Формирование биструктуры твердого тела в компьютерном эксперименте» . Физика твердого тела . 40 (10). Спрингер: 1742–1747. дои : 10.1134/1.1130648 . S2CID 121047989 .
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Подсчет многогранников
- Что такое многогранники? , с греческими цифровыми префиксами
Внешние ссылки
[ редактировать ] | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |