Тенсегрити

О системе движений, созданной Карлосом Кастанедой, см. Тенсегрити (Кастанеда) .

Простейшая структура тенсегрити (Т3-призма). Каждый из трех элементов сжатия (зеленый) симметричен двум другим и симметричен от конца до конца. Каждый конец соединен с тремя тросами (красными), которые обеспечивают натяжение и точно определяют положение этого конца точно так же, как три троса в Скайлоне определяют нижний конец его конической стойки.

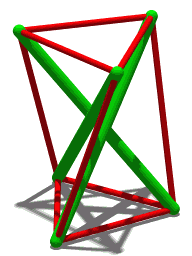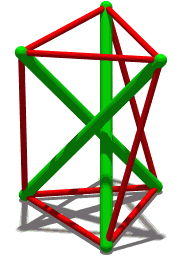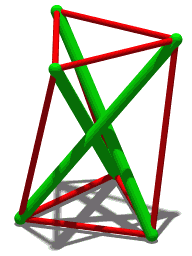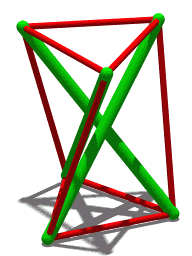
Стереоизображение
показывать Правый кадр
скрывать Левый кадр
показывать Вид косоглазия ( )
показывать Параллельный вид ( )
Анимация Похожая структура, но с четырьмя элементами сжатия.

Тенсегрити , целостность напряжения или плавающее сжатие — это структурный принцип, основанный на системе изолированных компонентов, находящихся под сжатием внутри сети постоянного напряжения , и расположенных таким образом, что сжатые элементы (обычно стержни или стойки) не касаются друг друга, пока предварительно напряженные натянутые элементы (обычно тросы или сухожилия) очерчивают систему в пространстве.

Структуры Тенсегрити встречаются как в природе, так и в объектах, созданных человеком: в человеческом теле кости сжимаются, а соединительные ткани — в напряжении, и те же принципы применяются к мебели, архитектурному дизайну и не только.

Этот термин был придуман Бакминстером Фуллером в 1960-х годах как сочетание «напряжённой целостности».

Основная концепция

Тенсегрити характеризуется несколькими основополагающими принципами, которые определяют его уникальные свойства:

1. Непрерывное натяжение . В основе тенсегрити лежат элементы натяжения — обычно тросы или сухожилия — образуют непрерывную сеть, охватывающую всю конструкцию. Это обеспечивает равномерное распределение механических напряжений и сохраняет форму конструкции, способствуя общей стабильности и гибкости системы.
2. Прерывистое сжатие : компоненты сжатия, такие как стойки или стержни, отличаются тем, что они не вступают в прямой контакт друг с другом, а вместо этого подвешиваются внутри натяжной сети. Это устраняет необходимость в жестких соединениях, повышая структурную эффективность и устойчивость системы.
3. Предварительное напряжение : Ключевым аспектом конструкций тенсегрити является их предварительно напряженное состояние, в котором натяжные элементы затягиваются в процессе сборки. Предварительное напряжение вносит значительный вклад в жесткость и стабильность конструкции, гарантируя, что все элементы постоянно находятся либо в растяжении, либо в сжатии.
4. Самоуравновешивание : Структуры Тенсегрити самоуравновешиваются и поэтому автоматически распределяют внутренние напряжения по всей структуре. Это позволяет им адаптироваться к изменяющимся нагрузкам без потери структурной целостности.
5. Минимализм и эффективность : системы Тенсегрити основаны на минималистской философии дизайна, используя минимальное количество материалов для достижения максимальной прочности конструкции.
6. Масштабируемость и модульность . Принципы проектирования тенсегрити допускают масштабируемость и модульную конструкцию. Структуры Тенсегрити легко адаптируются или расширяются по размеру и сложности в соответствии с конкретными требованиями.

Благодаря этим закономерностям ни один элемент конструкции не испытывает изгибающего момента не возникает касательных напряжений , и внутри системы . Это позволяет создавать исключительно прочные и жесткие конструкции по массе и поперечному сечению компонентов.

В совокупности эти принципы позволяют структурам тенсегрити достичь баланса силы, устойчивости и гибкости, что делает концепцию широко применимой в различных дисциплинах, включая архитектуру, робототехнику и биомеханику.

Ранний пример

Скайлон . на фестивале Британии , 1951 год

Концептуальный строительный блок тенсегрити можно увидеть в «Скайлоне» 1951 года . Шесть тросов , по три на каждом конце, удерживают башню на месте. Три кабеля, подключенные к нижней части, «определяют» ее местоположение. Остальные три троса просто удерживают его вертикально.

Структура тенсегрити из трех стержней (показанная выше на рисунке вращающейся призмы Т3) основана на этой более простой структуре: концы каждого зеленого стержня выглядят как верх и низ Скайлона. Пока угол между любыми двумя тросами меньше 180°, положение стержня четко определено. Хотя для устойчивости требуется минимум три кабеля, к каждому узлу можно подключить дополнительные кабели в эстетических целях и для резервирования . Например, « Игольная башня » Снельсона использует повторяющийся шаблон, построенный с использованием узлов, каждый из которых подключен к 5 кабелям.

Элеонора Хартни указывает на визуальную прозрачность как на важное эстетическое качество этих структур. Коркмаз и др. утверждал, что легкие структуры тенсегрити подходят для адаптивной архитектуры .

Приложения

Архитектура

Тенсегрити получил более широкое применение в архитектуре, начиная с 1960-х годов, когда Мацей Гинтовт и Мацей Красиньский спроектировали Сподек комплекс арены (в Катовице , Польша ) как одну из первых крупных структур, использующих принцип тенсегрити. Крыша представляет собой наклонную поверхность, удерживаемую системой тросов, удерживающих ее по окружности. Принципы Тенсегрити также использовались на Дэвида Гейгера Сеульской олимпийской гимнастической арене (для летних Олимпийских игр 1988 года ) и на стадионе «Джорджия Доум» (для летних Олимпийских игр 1996 года ). Тропикана Филд , домашний стадион бейсбольной команды высшей лиги Tampa Bay Rays, также имеет купольную крышу, поддерживаемую большой конструкцией тенсегрити.

Самый большой тенсегрити-мост в мире, мост Курилпа – Брисбен.

4 октября 2009 года открылся мост Курилпа через реку Брисбен в Квинсленде, Австралия . Многомачтовая вантовая конструкция, основанная на принципах тенсегрити, в настоящее время является крупнейшим в мире мостом тенсегрити.

Робототехника

— НАСА Super Ball Bot это ранний прототип, способный приземлиться на другую планету без подушки безопасности, а затем стать мобильным для исследования. Структура тенсегрити обеспечивает структурную податливость, поглощая силы удара при приземлении, а движение достигается за счет изменения длины троса, 2014 г.

С начала 2000-х годов тенсегрити также привлекли интерес робототехников из-за их потенциала в создании легких и устойчивых роботов. Многочисленные исследования исследовали марсоходы тенсегрити. биоимитирующие роботы, и модульные мягкие роботы. Самый известный робот тенсегрити — Super Ball Bot . марсоход для исследования космоса, использующий 6-барную тенсегрити-структуру , в настоящее время разрабатываемую в НАСА Эймс .

Анатомия

Биотенсегрити, термин, придуманный Стивеном Левином, представляет собой расширенное теоретическое применение принципов тенсегрити к биологическим структурам. Биологические структуры, такие как мышцы , кости , фасции , связки и сухожилия , а также жесткие и эластичные клеточные мембраны , становятся прочными благодаря сочетанию натянутых и сжатых частей. Скелетно -мышечная система состоит из непрерывной сети мышц и соединительных тканей. в то время как кости обеспечивают прерывистую компрессионную поддержку, в то время как нервная система поддерживает напряжение in vivo посредством электрического стимула. Левин утверждает, что человеческий позвоночник также представляет собой структуру тенсегрити, хотя со структурной точки зрения эта теория не подтверждается.

Биохимия

Дональд Э. Ингбер разработал теорию тенсегрити для описания многочисленных явлений, наблюдаемых в молекулярной биологии . клетки Например, выраженные формы клеток, будь то их реакции на приложенное давление, взаимодействие с субстратами и т. д., можно математически смоделировать, представляя цитоскелет в виде тенсегрити. Более того, геометрические узоры, встречающиеся в природе (спираль ДНК , геодезический купол вольвокса , бакминстерфуллерен и т. д.), также можно понять, основываясь на применении принципов тенсегрити к спонтанной самосборке соединений, белков, и даже органы. Эта точка зрения подтверждается тем, как взаимодействия растяжения и сжатия тенсегрити минимизируют количество материала, необходимого для поддержания стабильности и достижения структурной устойчивости, хотя сравнение с инертными материалами в биологической структуре не имеет широко принятой предпосылки в физиологической науке. Следовательно, давление естественного отбора , вероятно, будет благоприятствовать биологическим системам, организованным по принципу тенсегрити.

Как объясняет Ингбер:

Несущие напряжение элементы в этих структурах – будь то купола Фуллера или скульптуры Снельсона – прокладывают кратчайшие пути между соседними элементами (и, следовательно, по определению расположены геодезически). Силы растяжения естественным образом передаются по кратчайшему расстоянию между двумя точками, поэтому элементы структуры тенсегрити расположены точно так, чтобы лучше выдерживать нагрузки. По этой причине структуры тенсегрити предлагают максимальную силу.

В эмбриологии Ричард Гордон предположил, что волны эмбриональной дифференцировки распространяются с помощью «органеллы дифференцировки». где цитоскелет собран в бистабильную тенсегрити-структуру на апикальном конце клеток, называемую «разделителем состояний клетки».

Происхождение и история искусства

Проект X-модуля Кеннета Снельсона 1948 года, воплощенный в колонне из двух модулей.

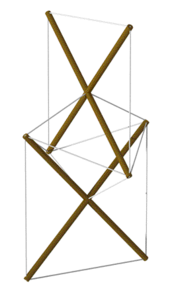
Истоки тенсегрити спорны. Многие традиционные конструкции, такие как каяки с обшивкой на раме и сёдзи , аналогичным образом используют элементы растяжения и сжатия.

Русский художник Вячеслав Колейчук утверждал, что идею тенсегрити впервые придумал Карлис Йохансонс (по-русски Карл Иогансон) ( lv ), советский -авангардист художник латышского происхождения, представивший несколько работ на главную выставку русского конструктивизма. в 1921 году. Заявление Колейчука поддержала Мария Гоф в отношении одной из работ конструктивистской выставки 1921 года. Снельсон признал, что конструктивисты оказали влияние на его работу (вопрос?). Французский инженер Давид Жорж Эммерих также отметил, что работа Карлиса Йохансона (и идеи промышленного дизайна), казалось, предвосхищала концепции тенсегрити.

Фактически, некоторые научные статьи доказывают этот факт, демонстрируя изображения первых конструкций Simplex (сделанных из 3 стержней и 9 сухожилий), разработанных Иогансоном.

В 1948 году художник Кеннет Снельсон создал свой новаторский «X-Piece» после художественных исследований в колледже Блэк-Маунтин (где Бакминстер Фуллер читал лекции) и в других местах. Несколько лет спустя термин «тенсегрити» был придуман Фуллером, который наиболее известен своими геодезическими куполами . На протяжении всей своей карьеры Фуллер экспериментировал с использованием растяжимых компонентов в своей работе, например, в каркасе своих из димаксиона . домов

Нововведение Снельсона 1948 года побудило Фуллера немедленно заказать у Снельсона мачту. В 1949 году Фуллер разработал на основе этой технологии тенсегрити- икосаэдр , и он и его ученики быстро разработали дальнейшие структуры и применили эту технологию для строительства куполов. После перерыва Снельсон также создал множество скульптур, основанных на концепциях тенсегрити. Его основная работа началась в 1959 году, когда ключевая выставка в Музее современного искусства состоялась . На выставке MOMA Фуллер показал мачту и некоторые другие свои работы. На этой выставке Снельсон, после обсуждения с Фуллером и организаторами выставки относительно признания мачты, также выставил некоторые работы в витрине .

высотой 26,5 метров (87 футов), Самым известным произведением Снельсона является его Игольная башня построенная в 1968 году.

Математика Тенсегрити

Нагрузка по крайней мере некоторых структур тенсегрити вызывает ауксетический ответ и отрицательный коэффициент Пуассона , например, призмы Т3 и икосаэдра тенсегрити с 6 стойками.

Тенсегрити призмы

Трехстержневая тенсегрити-структура (трехсторонняя призма) обладает тем свойством, что для заданной (общей) длины «стержня» сжимающего элемента (всего их три) и заданной (общей) длины натяжного троса «сухожилия» ( всего шесть), соединяющих концы стержней вместе, существует определенное значение (общей) длины сухожилия, соединяющего верхушки стержней с нижними частями соседних стержней, которое заставляет конструкцию сохранять стабильную форму. Для такой структуры несложно доказать, что треугольник, образованный вершинами стержней, и треугольник, образованный основаниями стержней, повернуты друг относительно друга на угол 5π/6 (радиан).

Стабильность («предварительно напряженная») нескольких двухэтапных структур тенсегрити проанализирована Султаном и др.

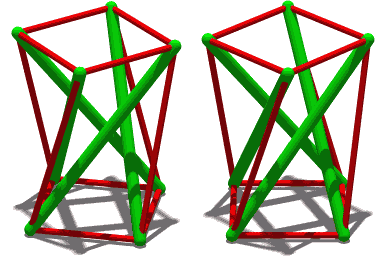
Призму Т3 (также известную как триплекс) можно получить, найдя форму прямой треугольной призмы. Его саморавновесное состояние задается, когда базовые треугольники находятся в параллельных плоскостях, разделенных углом поворота π/6. Формула его уникального состояния самонапряжения имеет вид: $$\omega =\omega _{1}[-{\sqrt {3}},-{\sqrt {3}},-{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},1,1,1,1,1,1]^{T}$$Здесь первые три отрицательных значения соответствуют внутренним компонентам при сжатии, а остальные соответствуют растяжению тросов.

Тенсегрити икосаэдры

Математическая модель тенсегрити-икосаэдра

Различные формы тенсегрити-икосаэдров в зависимости от соотношения длин сухожилий и стоек.

Тенсегрити-икосаэдр из соломинки и веревки.

Тенсегрити- икосаэдр , впервые изученный Снельсоном в 1949 году. имеет распорки и сухожилия по краям многогранника, называемого икосаэдром Джессена . Это устойчивая конструкция, хотя и с бесконечно малой подвижностью. Чтобы убедиться в этом, рассмотрим куб со стороной 2 d с центром в начале координат. Поместите распорку длиной 2 l в плоскость каждой грани куба так, чтобы каждая распорка была параллельна одному краю грани и находилась по центру грани. При этом каждая стойка должна быть параллельна стойке на противоположной грани куба, но ортогональна всем остальным стойкам. Если декартовы координаты одной стойки равны ⁠ $(0,d,l)$⁠ и ⁠ $(0,d,-l)$⁠ , то его параллельной стойки будут соответственно ⁠ $(0,-d,-l)$⁠ и ⁠ $(0,-d,l)$⁠ . Координаты остальных концов стойки (вершины) получаются перестановкой координат, например, ⁠ $(0,d,l)\rightarrow (d,l,0)\rightarrow (l,0,d)$⁠ (вращательная симметрия на главной диагонали куба).

Расстояние s между любыми двумя соседними вершинами (0, d , l ) и ( d , l , 0) равно

$$s^{2}=(d-l)^{2}+d^{2}+l^{2}=2\left(d-{\frac {1}{2}}\,l\right)^{2}+{\frac {3}{2}}\,l^{2}$$

Представьте себе эту фигуру, построенную из стоек заданной длины 2 l и сухожилий (соединяющих соседние вершины) заданной длины s , причем $s>{\sqrt {\frac {3}{2}}}\,l$. Соотношение говорит нам, что существует два возможных значения d : одно реализуется путем сближения стоек, другое — путем их разъединения. В частном случае $s={\sqrt {\frac {3}{2}}}\,l$ две крайности совпадают, и $d={\frac {1}{2}}\,l$, следовательно, фигура представляет собой устойчивый тенсегрити-икосаэдр. Этот выбор параметров придает вершинам положение икосаэдра Джессена; они отличаются от правильного икосаэдра , для которого соотношение $d$ и $l$ было бы золотым сечением , а не 2. Однако оба набора координат лежат в непрерывном семействе положений от кубооктаэдра до октаэдра ( как предельные случаи), которые связаны спиральным сжимающим/расширяющим преобразованием. Эта кинематика кубооктаэдра является геометрией движения тенсегрити-икосаэдра. Впервые он был описан HSM Coxeter. и позже названный Бакминстером Фуллером «трансформацией джиттербага».

Поскольку икосаэдр тенсегрити представляет собой экстремальную точку приведенного выше соотношения, он обладает бесконечно малой подвижностью: небольшое изменение длины s сухожилия (например, за счет растяжения сухожилий) приводит к гораздо большему изменению расстояния 2 d стоек.

Патенты

• Патент США № 3063521 «Конструкции, обеспечивающие целостность на растяжение», 13 ноября 1962 г., Бакминстер Фуллер.
• Патент Франции № 1 377 290, «Construction de Reseaux Autotendants», 28 сентября 1964 г., Дэвид Жорж Эммерих.
• Патент Франции № 1377291 «Автотендантные конструкции Linéaires», 28 сентября 1964 г., Дэвид Жорж Эммерих.
• Патент США № 3 139 957 «Подвесное здание» (также называемое осиной), 7 июля 1964 г., Бакминстер Фуллер.
• Патент США № 3169611 «Структура непрерывного растяжения и прерывистого сжатия», 16 февраля 1965 г., Кеннет Снельсон.
• Патент США № 3866366 «Несимметричные структуры, обеспечивающие целостность при растяжении», 18 февраля 1975 г., Бакминстер Фуллер.

Основные структуры тенсегрити

• 
  Простейшая структура тенсегрити — 3-призма.
• 
  Еще 3-призма
• 
  Аналогичная конструкция, но с четырьмя сжимающими элементами.
• 
  Призма Прото-Тенсегрити Карла Иогансона , 1921 год.
• 
  Тенсегрити Икосаэдр, Бакминстер Фуллер , 1949 год.
• 
  Тенсегрити Тетраэдр, Франческо делла Салла, 1952 год.
• 
  Тенсегрити X-Модуль Тетраэдр, Кеннет Снельсон , 1959 год.

Структуры Тенсегрити

• 
  Художественная скульптура Кеннета Снельсона «Игольная башня».
• 
  Купол тенсегрити из садовых кольев и нейлоновой веревки, построенный во дворе дома, 2009 г.
• 
  Выставка тенсегрити-структуры высотой 12 метров в городке Калькутты Научном .
• 
  Dissipate , художественная скульптура в виде башни песочных часов, включающая структуру тенсегрити, построенная на AfrikaBurn в 2015 году, Burning Man. региональном мероприятии

См. также

• Девятое облако — предлагаемые места обитания в воздухе . Страницы с краткими описаниями целей перенаправления , гигантские парящие в небе сферы тенсегрити, названные Бакминстером Фуллером.
• Гиперболоидная структура - тип неограниченного здания или сооружения квадратной формы.
• Теория взаимодействия акторов
• Двухскатная крыша - тип конструкции крыши. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Пространственная рама – жесткая трехмерная несущая ферменная конструкция.
• Синергетика - Эмпирическое исследование систем в процессе трансформации.
• Напряженность
• Растяжимая конструкция - Конструкция, элементы которой находятся только в напряжении.
• Структура с тонкой оболочкой – тонкостенное геометрическое твердое тело . Страницы с краткими описаниями целей перенаправления.
• Кинематика кубооктаэдра – Симметричные преобразования кубооктаэдра в связанные однородные многогранники, геометрия движения тенсегрити-икосаэдра

Библиография

• Фуллер, Р. Бакминстер (1961). «Тенсегрити» . Ежегодник портфолио и новостей искусства (4): 112–127, 144, 148.
• — (1982) [1975]. Синергетика: исследования в геометрии мышления . Том. И. Макмиллан. ISBN  978-0-02-065320-2 .
• — (1983) [1979]. Синергетика 2: Дальнейшие исследования геометрии мышления . Том. 2. Макмиллан. ISBN  978-0-02-092640-5 . Онлайн
• —; Маркс, Роберт В. (1973) [1960]. Мир Dymaxion Бакминстера Фуллера . Якорные книги. Рис. 261–280. ISBN  978-0-385-01804-3 . Хороший обзор масштабов тенсегрити с точки зрения Фуллера и интересный обзор ранних структур с тщательной атрибуцией в большинстве случаев.
• Кеннер, Хью (1976). Геодезическая математика и как ее использовать . Издательство Калифорнийского университета. ISBN  978-0-520-02924-8 . переиздание 2003 г. ISBN   0520239318 . Это хорошая отправная точка для изучения математики тенсегрити и построения моделей.
• Гомес-Хореги, Валентин (2007). Тенсегрити. Структуры Тенсегрити в науке и искусстве (на испанском языке). Сантандер: Университет Кантабрии. ISBN  978-84-8102-437-1 .
• — (2010). Структуры Тенсегрити и их применение в архитектуре . Сантандер: Служба публикаций Университета Кантабрии. ISBN  978-84-8102-575-0 .
• Гоф, Мария (весна 1998 г.). «В лаборатории конструктивизма: холодные конструкции Карла Иогансона». Октябрь . 84 : 90–117. дои : 10.2307/779210 . JSTOR   779210 .
• Хуан, С.Дж.; Тур, Дж. М. (июль 2008 г.). «Структуры Тенсегрити: обзор статического анализа». Теория механизма и машин . 43 (7): 859–81. CiteSeerX   10.1.1.574.7510 . doi : 10.1016/j.mechmachtheory.2007.06.010 .
• Коркмаз, Синан; Бел Хадж Али, Низар; Смит, Ян ФК (июнь 2011 г.). «Определение стратегий контроля устойчивости активной структуры Тенсегрити к повреждениям» (PDF) . Инженерные сооружения . 33 (6): 1930–1939. Бибкод : 2011EngSt..33.1930K . CiteSeerX   10.1.1.370.6243 . doi : 10.1016/j.engstruct.2011.02.031 . Архивировано из оригинала (PDF) 29 сентября 2011 года.
• —; —; - (январь 2012 г.). «Конфигурация системы управления устойчивостью к повреждениям моста Тенсегрити» . Высшая инженерная информатика . 26 (1): 145–155. дои : 10.1016/j.aei.2011.10.002 .
• Лалвани, Хареш, изд. (1996). «Происхождение Тенсегрити: взгляды Эммериха, Фуллера и Снельсона» . Международный журнал космических конструкций . 11 (1–2): 27–55. дои : 10.1177/026635119601-204 . S2CID   114004009 .
• Соуза, Фалес Р.; Фонсека, Сержио Т.; Гонсалвес, Габриэла Г.; Окарино, Джулиана М.; Манчини, Мариса К. (октябрь 2009 г.). «Предварительное напряжение проявляется пассивным ко-напряжением в голеностопном суставе» . Журнал биомеханики . 42 (14): 2374–80. doi : 10.1016/j.jbiomech.2009.06.033 . ПМИД   19647832 .

Дальнейшее чтение

• Эдмондсон, Эми (2007). «Более полное объяснение» , Emergent World LLC.
• Форбс, Питер (2010) [2006]. «9. Строительная система «Тяни и толкай»» . Нога геккона: как ученые извлекают лист из книги природы . Харпер Коллинз. стр. 197–230. ISBN  978-0-00-740547-3 .
• Ханаор, Ариэль (1997). «13. Тенсегрити: теория и применение» . В Габриэле, Ж. Франсуа (ред.). За пределами куба: архитектура пространственных рамок и многогранников . Уайли. стр. 385–408. ISBN  978-0-471-12261-6 .
• Масич, Миленко; Скелтон, Роберт Э.; Гилл, Филип Э. (август 2005 г.). «Алгебраическое нахождение формы тенсегрити». Международный журнал твердых тел и структур . 42 (16–17): 4833–4858. doi : 10.1016/j.ijsolstr.2005.01.014 . Они представили замечательный результат: любое линейное преобразование тенсегрити также является тенсегрити.
• Морган, Дж.Дж. (2003). «Исторический обзор: вирусы, кристаллы и геодезические купола» . Тенденции биохимических наук . 28 (2): 86–90. дои : 10.1016/S0968-0004(02)00007-5 . ПМИД   12575996 .
• Мотро, Р. (1992). «Системы Тенсегрити: современное состояние». Международный журнал космических конструкций . 7 (2): 75–84. дои : 10.1177/026635119200700201 . S2CID   107820090 .
• Пью, Энтони (1976). Введение в Тенсегрити . Издательство Калифорнийского университета. ISBN  978-0-520-03055-8 . Архивировано из оригинала 4 мая 2008 года . Проверено 9 мая 2008 г.
• Снельсон, Кеннет (ноябрь 1990 г.). «Письмо Р. Мотро» . Международный журнал космических конструкций .
• Вильней, Орен (1990). Кабельные сети и тенсегриковые оболочки: приложения для анализа и проектирования , Нью-Йорк: Ellis Horwood Ltd.
• Ван, Бин-Бин (1998). «Вантово-стоечные системы: Часть I – Тенсегрити». Журнал исследований конструкционной стали . 45 (3): 281–89. дои : 10.1016/S0143-974X(97)00075-8 .
• Уилкен, Тимоти (2001). В поисках дара Тенсегрити , TrustMark

Внешние ссылки

• Научные публикации в области Тенсегрити Швейцарского федерального технологического института (EPFL), Лаборатории прикладных вычислений и механики (IMAC)
• Сайт Стивена Левина по биотенсегрити Несколько статей хирурга-ортопеда о механике тенсегрити биологических структур от вирусов до позвоночных.