Натяжная конструкция

В строительной технике натяжная конструкция представляет собой конструкцию из элементов, несущих только растяжение , но не сжимающих и не изгибающих . Термин «растяжение» не следует путать с тенсегрити , которая представляет собой структурную форму с элементами как растяжения, так и сжатия. Натяжные конструкции являются наиболее распространенным типом тонкостенных конструкций .

Большинство растяжимых конструкций поддерживаются той или иной формой сжимающих или изгибающих элементов, таких как мачты (как в The O ₂ , ранее называвшийся « Купол Тысячелетия» ), сжимающие кольца или балки.

натяжные мембранные конструкции чаще всего используют В качестве крыши , поскольку они позволяют экономично и привлекательно перекрывать большие расстояния. Натяжные мембранные конструкции также могут использоваться в качестве полноценных зданий, причем некоторые распространенные применения — это спортивные сооружения, складские и складские здания, а также выставочные площадки. ^[1]

История

Эта форма конструкции стала более тщательно анализироваться и широко распространяться в крупных сооружениях только во второй половине двадцатого века. издавна используются натяжные конструкции В палатках , где растяжки и стойки палатки обеспечивают предварительное натяжение ткани и позволяют ей выдерживать нагрузки.

Русский инженер Владимир Шухов одним из первых разработал практические расчеты напряжений и деформаций натяжных конструкций, оболочек и оболочек. натяжных и тонкостенных конструкций Шухов спроектировал восемь выставочных павильонов для Нижегородской ярмарки 1896 года площадью 27 000 квадратных метров. Более поздним крупномасштабным использованием натяжной конструкции с мембранным покрытием является Sidney Myer Music Bowl , построенный в 1958 году.

Антонио Гауди использовал эту концепцию наоборот, чтобы создать структуру, предназначенную только для сжатия, для церкви Колония Гуэль . Он создал висячую растянутую модель церкви, чтобы рассчитать силы сжатия и экспериментально определить геометрию колонн и свода.

Позднее эту концепцию поддержал немецкий архитектор и инженер Фрей Отто , который впервые использовал эту идею при строительстве западногерманского павильона на выставке Expo 67 в Монреале. Затем Отто использовал эту идею для крыши Олимпийского стадиона на летних Олимпийских играх 1972 года в Мюнхене .

С 1960-х годов натяжные конструкции продвигали такие дизайнеры и инженеры, как Уве Аруп , Буро Хаппольд , Уолтер Берд из Birdair, Inc. , Фрей Отто , Махмуд Бодо Раш , Ээро Сааринен , Хорст Бергер , Мэтью Новицки , Йорг Шлайх , дуэт Николаса Голдсмита и Тодда Далланда из FTL Design & Engineering Studio и Дэвида Гейгера .

Устойчивый технический прогресс увеличил популярность конструкций с тканевой кровлей. Малый вес материалов упрощает и удешевляет строительство по сравнению со стандартными конструкциями, особенно когда необходимо покрыть большие открытые пространства.

Типы конструкций со значительными напряжениями элементов

Линейные структуры

Подвесные мосты
Напряженный ленточный мост
Драпированные кабели
Вантовые балки или фермы
Кабельные фермы
Прямые натянутые тросы

Трехмерные структуры

Велосипедное колесо (можно использовать как крышу в горизонтальном положении)
3D кабельные фермы
Тенсегрити Структуры

Поверхностно-напряженные конструкции

Предварительно напряженные мембраны
Пневмонапряженные мембраны
Сетка
Структура ткани

Кабельные и мембранные конструкции

Мембранные материалы

Обычными материалами для тканевых конструкций двойной кривизны являются из ПТФЭ с покрытием стекловолокно и из ПВХ с покрытием полиэстер . Это тканые материалы, имеющие разную прочность в разных направлениях. Волокна основы (те волокна, которые изначально прямые — эквивалент исходных волокон на ткацком станке) могут выдерживать большую нагрузку, чем волокна утка или наполнителя, которые вплетены между волокнами основы.

В других конструкциях используется пленка ETFE либо в виде однослойной, либо в виде подушки (которую можно надувать для обеспечения хороших изоляционных свойств или для эстетического эффекта, как на «Альянц Арене» в Мюнхене ). На подушках из ETFE также можно выгравировать узоры, чтобы пропускать разные уровни света при надувании до разных уровней.

При дневном свете полупрозрачность тканевой мембраны создает мягкое рассеянное естественное освещение, а ночью можно использовать искусственное освещение для создания окружающего внешнего свечения. Чаще всего они поддерживаются структурным каркасом, поскольку не могут получить свою прочность за счет двойной кривизны. ^[2]

Простой подвесной мост, работающий полностью на растяжение

Кабели

Тросы могут быть изготовлены из мягкой стали , высокопрочной стали (тянутой углеродистой стали), нержавеющей стали , полиэфирных или арамидных волокон . Структурные тросы состоят из серии небольших прядей, скрученных или связанных вместе, образуя кабель гораздо большего размера. Стальные тросы представляют собой либо спиральную прядь, в которой круглые стержни скручены вместе и «склеены» с помощью полимера, либо прядь с замком витка, где отдельные переплетающиеся стальные пряди образуют кабель (часто со спиральным сердечником).

Спиральная прядь немного слабее, чем закрепленная спиральная прядь. Стальные спиральнопрядные кабели имеют модуль Юнга . E 150±10 кН/мм ² (или 150±10 ГПа ) и имеют размеры от 3 до 90 мм в диаметре. ^{[ нужна ссылка ]} Спиральная прядь подвергается строительному растяжению, при котором пряди сжимаются при нагрузке кабеля. Обычно это устраняется путем предварительного растяжения троса и циклического увеличения и уменьшения нагрузки до 45 % от предельной растягивающей нагрузки.

Замкнутая спиральная прядь обычно имеет модуль Юнга 160 ± 10 кН/мм. ² и поставляется в размерах от 20 мм до 160 мм в диаметре.

Свойства отдельных прядей из разных материалов приведены в таблице ниже, где UTS — предел прочности на разрыв , или разрывная нагрузка:

Материал кабеля	Е (ГПа)	УТС (МПа)	Деформация при 50% UTS
Твердый стальной стержень	210	400–800	0.24%
Стальная прядь	170	1550–1770	1%
Трос	112	1550–1770	1.5%
Полиэфирное волокно	7.5	910	6%
Арамидное волокно	112	2800	2.5%

Структурные формы

Воздухоопорные конструкции представляют собой разновидность натяжных конструкций, в которых тканевая оболочка поддерживается только воздухом под давлением.

Большинство тканевых структур черпают свою силу из своей двояко изогнутой формы. Заставляя ткань принимать двойную кривизну, ткань приобретает достаточную жесткость , чтобы выдерживать нагрузки, которым она подвергается (например, ветровые и снеговые нагрузки). Для того чтобы придать соответствующую двойную изогнутую форму, чаще всего необходимо предварительно натянуть ткань или ее опорную конструкцию.

Поиск формы

Поведение конструкций, прочность которых зависит от предварительного напряжения, является нелинейным, поэтому до 1990-х годов было очень сложно спроектировать что-либо, кроме очень простого троса. Самым распространенным способом проектирования тканевых конструкций двойной кривизны было построение масштабных моделей готовых зданий, чтобы понять их поведение и провести упражнения по поиску формы. В таких масштабных моделях часто использовались чулочные материалы, колготки или мыльная пленка, поскольку они ведут себя очень похоже на конструкционные ткани (они не выдерживают сдвига).

Мыльные пленки имеют равномерное напряжение во всех направлениях, и для их формирования требуется замкнутая граница. Они естественным образом образуют минимальную поверхность — форму с минимальной площадью и воплощающую минимальную энергию. Однако их очень трудно измерить. Для большой пленки ее вес может серьезно повлиять на ее форму.

Для мембраны с кривизной в двух направлениях основное уравнение равновесия имеет вид:

w={\frac {t_{1}}{R_{1}}}+{\frac {t_{2}}{R_{2}}}

где:

R ₁ и R ₂ — главные радиусы кривизны мыльных пленок или направления основы и утка для тканей.
t ₁ и t ₂ — напряжения в соответствующих направлениях
w — нагрузка на квадратный метр

Линии главной кривизны не имеют закручивания и пересекают другие линии главной кривизны под прямым углом.

Геодезическая геодезическая или линия обычно представляет собой кратчайшую линию между двумя точками на поверхности. Эти линии обычно используются при определении линий швов схемы раскроя. Это связано с их относительной прямолинейностью после создания плоских полотен, что приводит к уменьшению отходов ткани и более точному совмещению с переплетением ткани.

На предварительно напряженной, но ненагруженной поверхности w = 0, поэтому ${\frac {t_{1}}{R_{1}}}=-{\frac {t_{2}}{R_{2}}}$ .

В мыльной пленке поверхностное натяжение одинаково в обоих направлениях, поэтому R ₁ = − R ₂ .

Теперь можно использовать мощные нелинейного численного анализа программы (или анализа методом конечных элементов ) для поиска и проектирования тканевых и кабельных конструкций. Программы должны допускать большие отклонения.

Окончательная форма или форма тканевой конструкции зависит от:

форма или рисунок ткани
геометрия несущей конструкции (например, мачты, тросы, кольцевые балки и т. д.)
предварительное натяжение, приложенное к ткани или ее несущей конструкции

Важно, чтобы окончательная форма не допускала скопления воды, так как это может деформировать мембрану и привести к локальному разрушению или прогрессирующему разрушению всей конструкции.

Снеговая нагрузка может стать серьезной проблемой для мембранной конструкции, поскольку снег часто не стекает с конструкции в отличие от воды. Например, в прошлом это приводило к (временному) обрушению Метродома Хьюберта Х. Хамфри , надутой воздухом конструкции в Миннеаполисе, штат Миннесота . Некоторые сооружения, склонные к затоплению, используют отопление для таяния оседающего на них снега.

Существует множество различных двоякоизогнутых форм, многие из которых обладают особыми математическими свойствами. Самая основная форма двойной изогнутости - это форма седла, которая может представлять собой гиперболический параболоид (не все формы седла являются гиперболическими параболоидами). Это поверхность с двойной линейкой , и она часто используется в обоих случаях в легких конструкциях оболочек (см. Гиперболоидные конструкции ). Настоящие линейчатые поверхности редко встречаются в натяжных конструкциях. Другими формами являются антикластические седла, различные радиальные, конические шатровые формы и любые их комбинации.

Претензия

Предварительное натяжение — это напряжение, искусственно создаваемое в элементах конструкции в дополнение к любому собственному весу или нагрузкам, которые они могут нести. Он используется для того, чтобы обычно очень гибкие элементы конструкции оставались жесткими при всех возможных нагрузках. ^[3]^[4]

Повседневным примером претенциозности является стеллаж, поддерживаемый проводами, идущими от пола до потолка. Тросы удерживают полки на месте, потому что они натянуты — если бы провода провисли, система не работала бы.

Предварительное натяжение можно приложить к мембране, растягивая ее по краям или предварительно натягивая тросы, поддерживающие ее, и, следовательно, изменяя ее форму. Уровень приложенного предварительного натяжения определяет форму мембранной конструкции.

Альтернативный подход к поиску формы

Альтернативный приближенный подход к решению задачи формообразования основан на полном энергетическом балансе сеточно-узловой системы. По своему физическому смыслу этот подход называется методом растянутой сетки (МРГ).

Простая математика кабелей

Поперечно и равномерно нагруженный кабель

Равномерно нагруженный трос, протянутый между двумя опорами, образует промежуточную кривую между цепной линией и параболой . Можно сделать упрощающее предположение, что оно аппроксимирует дугу окружности (радиуса R ).

По равновесию :

Горизонтальная и вертикальная реакции:

H={\frac {wS^{2}}{8d}}

V={\frac {wS}{2}}

По геометрии :

Длина кабеля:

L=2R\arcsin {\frac {S}{2R}}

Натяжение троса:

T={\sqrt {H^{2}+V^{2}}}

По замене:

T={\sqrt {\left({\frac {wS^{2}}{8d}}\right)^{2}+\left({\frac {wS}{2}}\right)^{2}}}

Напряжение также равно:

T=wR

Удлинение троса при нагрузке равно (из закона Гука , где осевая жесткость k равна $k={\frac {EA}{L}}$ ):

e={\frac {TL}{EA}}

где E — модуль Юнга кабеля, а A его поперечного сечения — площадь .

Если первоначальная претензия, $T_{0}$ добавляется к кабелю, расширение становится:

e=L-L_{0}={\frac {L_{0}(T-T_{0})}{EA}}

Объединение приведенных выше уравнений дает:

{\frac {L_{0}(T-T_{0})}{EA}}+L_{0}={\frac {2T\arcsin \left({\frac {wS}{2T}}\right)}{w}}

Построив левую часть этого уравнения в зависимости от Т и отложив правую часть по тем же осям, а также в зависимости от Т, пересечение даст фактическое равновесное натяжение в кабеле для заданной нагрузки w и заданного предварительного натяжения. $T_{0}$ .

Кабель с центральной точечной нагрузкой

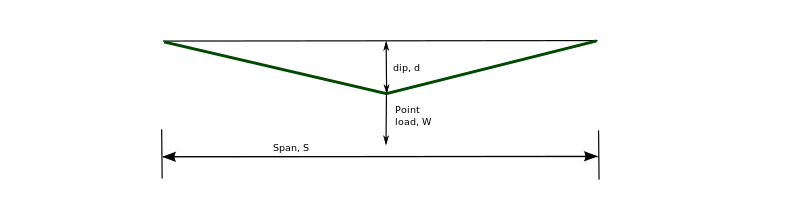
Решение, аналогичное приведенному выше, может быть получено, если:

По равновесию:

W={\frac {4Td}{L}}

d={\frac {WL}{4T}}

По геометрии:

L={\sqrt {S^{2}+4d^{2}}}={\sqrt {S^{2}+4\left({\frac {WL}{4T}}\right)^{2}}}

Это дает следующее соотношение:

L_{0}+{\frac {L_{0}(T-T_{0})}{EA}}={\sqrt {S^{2}+4\left({\frac {W(L_{0}+{\frac {L_{0}(T-T_{0})}{EA}})}{4T}}\right)^{2}}}

Как и раньше, построение графика левой и правой частей уравнения в зависимости от натяжения T даст равновесное натяжение для данного предварительного натяжения: $T_{0}$ и нагрузка, Вт .

Колебания натянутого троса

Основная частота собственная f ₁ натянутых кабелей определяется по формуле:

f_{1}={\frac {\sqrt {\left({\frac {T}{m}}\right)}}{2L}}

где T = напряжение в ньютонах , m = масса в килограммах и L = длина пролета.

Известные структуры

Шуховская Ротонда , Россия , 1896 год.
Canada Place , Ванкувер , Британская Колумбия, на выставке Expo '86
Национальная гимназия Ёёги Кензо Танге , парк Ёёги , Токио , Япония
Ингаллс Ринк , Йельский университет, автор Ээро Сааринен
Развлекательный центр «Хан Шатыр» , Астана, Казахстан
Тропикана Филд , Санкт-Петербург , Флорида
Олимпийский парк , Мюнхен, автор Фрей Отто
Сидни Майер Мьюзик Боул , Мельбурн
O ₂ (ранее Millennium Dome ), Лондон, партнерство Buro Happold и Richard Rogers.
Международный аэропорт Денвера , Денвер
Дортон Арена , Роли
Georgia Dome , Атланта , Джорджия, компания Heery and Weidlinger Associates (снесена в 2017 году)
Международный аэропорт Грантли Адамс , Крайст-Черч , Барбадос
Pengrowth Saddledome , Калгари, архитекторы Graham McCourt Architects и Jan Bobrowski and Partners.
Скандинавиум , Гетеборг , Швеция
Гонконгский музей береговой обороны
Модернизация центрального железнодорожного вокзала , София , Болгария
Redbird Arena , Университет штата Иллинойс , Нормал, Иллинойс
Выдвижные зонтики, Аль-Масджид ан-Набави , Медина, Саудовская Аравия
Башня Киллесберг , Штутгарт

Галерея известных натяжных конструкций

Натяжные конструкции крыши Фрея Отто Олимпийского парка . в Мюнхене
« Купол тысячелетия» (ныне The O ₂ ), Лондон , авторы Буро Хаппольд и Ричард Роджерс.
международного аэропорта Денвера Терминал
THTR -300 с кабельной сетью Сухая градирня , гиперболоидная конструкция от Schlaich Bergermann & Partner.
Башня Киллесберг, Штутгарт, партнер Schlaich Bergermann
Джорджия Доум в Атланте
Дневной компьютерный рендеринг — развлекательного центра «Хан Шатыр» самой высокой натяжной конструкции в мире.

Классификационные номера

Институт строительных спецификаций (CSI) и Строительные спецификации Канады (CSC), MasterFormat 2018 Edition, Division 05 и 13:

05 16 00 – Структурная кабельная система
05 19 00 – Натяжные стержни и вантовые фермы в сборе
13 31 00 – Тканевые конструкции
13 31 23 – Натянутые тканевые конструкции
13 31 33 – Каркасные тканевые конструкции

CSI/CSC MasterFormat, издание 1995 г.:

13120 – Вантовые конструкции
13120 – Тканевые конструкции

См. также

Ссылки

^ plc, Коллинсон. «Растяжимые тканевые конструкции: полное руководство (новинка 2018 года)» . info.collinson.co.uk . Проверено 2 июля 2018 г.
^ «Подпрыгнул» . Армейские технологии .
^ Квальяроли, М.; Малерба, PG; Альбертен, А.; Поллини, Н. (01 декабря 2015 г.). «Роль предварительного напряжения и его оптимизация при проектировании вантовых куполов» . Компьютеры и конструкции . 161 : 17–30. doi : 10.1016/j.compstruc.2015.08.017 . ISSN 0045-7949 .
^ Альбертен, А; Малерба, П; Поллини, Н; Квальяроли, М. (21 июня 2012 г.), «Оптимизация предварительного напряжения гибридных натяжных конструкций» , Техническое обслуживание мостов, безопасность, управление, отказоустойчивость и устойчивость , CRC Press, стр. 1750–1757, doi : 10.1201/b12352-256 , ISBN 978-0-415-62124-3 , получено 30 июня 2020 г.

Дальнейшее чтение

«Нижне-Новгородская выставка: Водонапорная башня, строящееся помещение, пружина пролетом 91 фут», «Инженер» , № 19.3.1897, стр.292-294, Лондон, 1897.
Хорст Бергер , Легкие конструкции, конструкции света: Искусство и инженерия натяжной архитектуры (Birkhäuser Verlag, 1996). ISBN 3-7643-5352-X
Алан Холгейт, Искусство строительного проектирования: работа Йорга Шлайха и его команды (Books Britain, 1996) ISBN 3-930698-67-6
Элизабет Купер Инглиш : «Архитектура и мнести»: Истоки советской авангардной рационалистической архитектуры в русской мистико-философской и математической интеллектуальной традиции» , диссертация по архитектуре, 264 стр., Пенсильванский университет, 2000.
«Владимир Г. Сухов 1853–1939. Искусство экономичного строительства», Райнер Грефе, Йос Томлов и др., 192 стр., Deutsche Verlags-Anstalt, Штутгарт, 1990, ISBN 3-421-02984-9 .
Конрад Роланд : Фрей Отто – Спанс. Идеи и попытки облегчения конструкции . Отчет о семинаре Конрада Роланда. Ульштейн, Берлин, Франкфурт-на-Майне и Вена, 1965 г.
Фрей Отто, Бодо Раш: В поисках формы - к архитектуре минимального, издание Акселя Менгеса, 1996, ISBN 3930698668
Нердингер, Винфрид: Фрей Отто. Полное собрание сочинений: Стройте легко, проектируйте естественно, 2005 г., ISBN 3-7643-7233-8

[1] , Коллинсон. «Растяжимые тканевые конструкции: полное руководство (новинка 2018 года)» . info.collinson.co.uk . Проверено 2 июля 2018 г.

[2] «Подпрыгнул» . Армейские технологии .

[3] Квальяроли, М.; Малерба, PG; Альбертен, А.; Поллини, Н. (01 декабря 2015 г.). «Роль предварительного напряжения и его оптимизация при проектировании вантовых куполов» . Компьютеры и конструкции . 161 : 17–30. doi : 10.1016/j.compstruc.2015.08.017 . ISSN 0045-7949 .

[4] Альбертен, А; Малерба, П; Поллини, Н; Квальяроли, М. (21 июня 2012 г.), «Оптимизация предварительного напряжения гибридных натяжных конструкций» , Техническое обслуживание мостов, безопасность, управление, отказоустойчивость и устойчивость , CRC Press, стр. 1750–1757, doi : 10.1201/b12352-256 , ISBN 978-0-415-62124-3 , получено 30 июня 2020 г.

[1]

[2]

[3]

[4]