Метод растянутой сетки

Метод растянутой сетки ( SGM ) — это численный метод поиска приближенных решений различных математических и инженерных задач, которые могут быть связаны с поведением упругой сетки.В частности, метеорологи используют метод растянутой сетки для прогнозирования погоды. а инженеры используют метод натянутой сетки для проектирования палаток и других натяжных конструкций .

Уточнение сетки МКЭ и БЭМ

В последние десятилетия методы конечных и граничных элементов (МКЭ и БЭМ) стали основой промышленного проектирования и анализа. С помощью FEM или BEM моделируются все более крупные и сложные конструкции. Однако некоторые проблемы инженерного анализа МКЭ и БЭМ все еще остаются актуальными. Первая проблема — надежность инженерного анализа, которая сильно зависит от качества исходных данных, формируемых на этапе предварительной обработки. Известно, что методы автоматического построения сетки элементов на данном этапе стали широко используемыми инструментами анализа сложных моделей реального мира. С ростом популярности FEM и BEM появляется стимул для улучшения алгоритмов автоматического построения сетки. Однако все эти алгоритмы могут создавать искаженные и даже непригодные для использования элементы сетки. Существует несколько методов, которые позволяют использовать существующую сетку и улучшить ее качество. Например, сглаживание (также называемое уточнением сетки ) является одним из таких методов, который меняет положение узлов, чтобы минимизировать искажение элемента. Метод растянутой сетки (SGM) позволяет очень легко и быстро получать псевдорегулярные сетки за один шаг (см. ).

Предположим, что имеется произвольная треугольная сетка, вложенная в плоский полигональный однокогерентный контур и созданная с помощью процедуры авторазбивки (см. рис. 1). Далее можно предположить, что сетка, рассматриваемая как физическая узловая система, искажена рядом искажения. Предполагается, что полная потенциальная энергия этой системы пропорциональна длине некоторого $\ n$-мерный вектор, компонентами которого являются все сегменты сети.

Рис. 1 Треугольная сетка, ограниченная плоским полигональным однокогерентным контуром

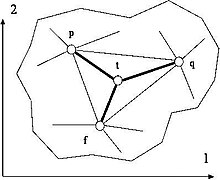
Таким образом, потенциальная энергия принимает следующий вид

$\Pi =D\sum _{j=1}^{n}{R_{j}}^{2}$

где

• $\ n$ - общее количество сегментов в сети,
• $\ R_{j}$ - Длина номера сегмента $\ j$,
• $\ D$ - произвольная константа.

Длина номера сегмента $\ j$ может быть выражено двумя узловыми координатами как

$\ R={\sqrt {(X_{12}-X_{11})^{2}+(X_{22}-X_{21})^{2}}}$

Можно также предположить, что вектор координат $\{\ X\}$ всех узлов связан с неискаженной сетью и вектором координат $\{\ X'\}$ связано с искаженной сетью. Выражение для вектора $\{\ X\}$ может быть записано как

$\{\ X\}=\{\ X'\}+\{\Delta \ X\}$

Вектор $\{\ X\}$ определение связано с минимизацией квадратичной формы $\ \Pi$ по инкрементному вектору $\{\Delta \ X\}$, то есть

${\frac {\partial \Pi }{\partial \Delta X_{kl}}}=0$

где

• $\ l$ - номер внутреннего узла области,
• $\ k$ - количество координат

После всех преобразований мы можем записать следующие две независимые системы линейных алгебраических уравнений:

$[\ A]\{\Delta X_{1}\}=\{\ B_{1}\}$

$[\ A]\{\Delta X_{2}\}=\{\ B_{2}\}$

где

• $[\ A]$ - симметричная матрица в полосчатой ​​форме, аналогичная глобальной матрице жесткости сборки МКЭ,
• $\{\Delta \ X_{1}\}$ и $\{\Delta \ X_{2}\}$- инкрементные векторы координат всех узлов по осям 1, 2,
• $\{\ B_{1}\}$ и $\{\ B_{2}\}$ - векторы правой части, объединяемые координатами всех узлов в осях 1, 2.

Рис. 2. Слева: искаженная 2D-сетка, справа: исправленная сетка.

Решение обеих систем, сохраняя консервативность всех граничных узлов, позволяет получить новые внутренние позиции узлов, соответствующие неискаженной сетке с псевдорегулярными элементами. Например, на рис. 2 представлена ​​прямоугольная область, покрытая треугольной сеткой. Исходная автоматическая сетка содержит несколько вырожденных треугольников (левая сетка). Итоговая сетка (правая сетка), полученная с помощью процедуры SGM, является псевдорегулярной без каких-либо искаженных элементов.

Поскольку описанные выше системы линейны, процедура очень быстро сводится к одноэтапному решению. Более того, каждое конечное положение внутреннего узла удовлетворяет требованию среднего арифметического координат окружающих его узлов, а также критериям Делоне . Таким образом, SGM имеет все положительные значения, свойственные лапласиану и другим подходам сглаживания, но намного проще и надежнее из-за целочисленного представления конечных матриц. Наконец, описанная выше SGM прекрасно применима не только к 2D-сеткам, но и к 3D-сеткам, состоящим из любых однородных ячеек, а также к смешанным или переходным сеткам.

Решение проблемы с минимальной поверхностью

Математически поверхность, вложенная в неплоскую замкнутую кривую, называется минимальной, если ее площадь минимальна среди всех поверхностей, проходящих через эту кривую. Самый известный образец минимальной поверхности — это мыльная пленка, ограниченная проволочным каркасом. Обычно для создания минимальной поверхности используется фиктивный конститутивный закон, который поддерживает постоянное предварительное напряжение, независимое от каких-либо изменений деформации. Альтернативный приближенный подход к решению задачи минимальной поверхности основан на SGM. Данная формулировка позволяет минимизировать поверхность, вложенную в неплоские и плоские замкнутые контуры.

Рис. 3. Катеноидальная поверхность

Идея состоит в том, чтобы аппроксимировать часть поверхности, встроенную в трехмерный неплоский контур, произвольной треугольной сеткой. Чтобы сходиться такая треугольная сетка к сетке минимальной площади, необходимо решить те же две системы, описанные выше. Приращения третьих узловых координат могут быть дополнительно определены по аналогичной системе на оси 3 следующим образом:

$[\ A]\{\Delta X_{3}\}=\{\ B_{3}\}$

Решая одновременно все три системы, можно получить новую сетку, которая будет аппроксимирующей минимальной поверхностью, вложенной в неплоскую замкнутую кривую, из-за минимума функции $\ \Pi$ где параметр $\ j=1,2,3$.

В качестве примера на рис. 3 представлена ​​поверхность катеноида , рассчитанная описанным выше подходом. Радиусы колец и высота катеноида равны 1,0. Численная площадь катеноидальной поверхности, определенная СГМ, равна 2,9967189 (точное значение 2,992).

Нахождение формы натяжных тканевых конструкций

Рис. 4 Гипар (гиперболический параболоид)

Рис. 5 Маркиза седельного типа

Для структурного анализа конфигурация конструкции обычно известна априори. Это не относится к натяжным конструкциям, таким как натяжные тканевые конструкции . Поскольку мембрана в натяжной конструкции не обладает жесткостью при изгибе, ее форма или конфигурация зависят от первоначального предварительного напряжения и нагрузок, которым она подвергается. Таким образом, несущая способность и форма мембраны не могут быть разделены и не могут быть описаны только простыми геометрическими моделями. Форма мембраны, нагрузки на конструкцию и внутренние напряжения взаимодействуют нелинейным образом, удовлетворяя уравнениям равновесия.

Рис. 6. Модель сетки покрытия танцпола.

Рис. 7 Рендер обложки танцпола

Рис. 8. Реальное покрытие для танцпола.

Предварительное проектирование натяжных конструкций предполагает определение исходной конфигурации, называемое поиском формы. Помимо удовлетворения условий равновесия, первоначальная конфигурация должна учитывать как архитектурные (эстетические), так и конструктивные (прочность и устойчивость) требования. Кроме того, должны быть соблюдены требования к пространству и зазору, главные напряжения мембраны должны быть растягивающими, чтобы избежать образования складок, а радиусы двойной криволинейной поверхности должны быть достаточно малы, чтобы противостоять нагрузкам вне плоскости и обеспечивать устойчивость конструкции ( работа ). Несколько вариантов подходов к поиску формы, основанных на МКЭ, были разработаны для помощи инженерам в проектировании натяжных тканевых конструкций. Все они основаны на тех же предположениях, что и при анализе поведения натяжных конструкций при различных нагрузках. Однако, как отмечают некоторые исследователи, иногда может быть предпочтительнее использовать так называемые « минимальные поверхности при проектировании натяжных конструкций ».

Физический смысл СГМ состоит в стремлении энергии произвольной сеточной структуры, вложенной в жесткий (или упругий) трехмерный контур, к минимуму, что эквивалентно минимальной сумме расстояний между произвольными парами узлов сетки. Это позволяет решить задачу минимальной поверхностной энергии, заменяя поиск минимума суммарной энергии структуры сетки, что обеспечивает гораздо более простую окончательную систему алгебраических уравнений, чем обычная формулировка FEM. Обобщенная формулировка SGM предполагает возможность применения набора внешних сил и жестких или упругих ограничений к узлам сеточной структуры, что позволяет моделировать различные внешние эффекты. Для такой формулировки SGM мы можем получить следующее выражение

$\Pi =\sum _{j=1}^{n}D_{j}R_{j}^{2}+\sum _{i=1}^{3}\left(\sum _{k=1}^{m}C_{ik}\Delta X_{ik}^{2}-\sum _{k=1}^{m}P_{ik}\Delta X_{ik}\right)$

где

• $\ n$ - общее количество сегментов сетки,
• $\ m$ - общее количество узлов,
• $\ R_{j}$ - длина номера сегмента $\ j$,
• $\ D_{j}$ - жесткость номера сегмента $\ j$,
• $\ \Delta X_{ik}$ - приращение координат узла $\ k$ на оси $\ i$,
• $\ C_{ik}$ - жесткость упругой связи в узле $\ k$ на оси $\ i$,
• $\ P_{ik}$ - внешняя сила в узле $\ k$ на оси $\ i$.

Раскрытие проблемы и создание схемы резки

Как только будет найдена удовлетворительная форма, шаблон для резки можно создать . Натяжные конструкции сильно различаются по своим размерам, кривизне и жесткости материала. Аппроксимация схемы резки тесно связана с каждым из этих факторов. Для метода создания схемы раскроя важно минимизировать возможную аппроксимацию и получить надежные данные о плоской ткани.

Цель состоит в том, чтобы разработать формы, описываемые этими данными, как можно более близкие к идеальным полосам двоякой кривизны. В общем, создание схемы резки включает в себя два этапа. Сначала глобальная поверхность натяжной конструкции разбивается на отдельные полотна. Соответствующую схему раскроя на втором этапе можно найти, просто взяв каждую полоску ткани и развернув ее на плоском участке. В случае идеальной двоякоизогнутой поверхности мембраны подповерхность невозможно просто развернуть, и ее необходимо сгладить. Например, в, SGM использовался для решения проблемы сглаживания.

Задача формирования схемы раскроя фактически подразделяется на две независимые постановки. Это создание плоской формы без искажений, разворачивающей каждую полоску ткани и сглаживающей двояковыпуклые поверхности, которые невозможно просто развернуть. Внимательно изучая задачу, можно заметить, что с позиции дифференциальной геометрии обе постановки одинаковы. Мы можем рассматривать его как изометрическое отображение поверхности на плоскую площадь, которое будет одновременно конформным и равноплощадным отображением из-за инвариантности углов между любыми кривыми и инвариантности любых участков площади. В случае однокриволинейной поверхности, которую можно точно развернуть, равноплощадное картографирование позволяет получить схему раскроя структуры ткани без каких-либо искажений. Поверхности второго типа могут быть равноплощадными отображены лишь приблизительно с некоторыми искажениями линейных элементов поверхности, ограниченными свойствами ткани. Предположим, что две поверхности параметризованы так, что их первые квадратичные формы можно записать следующим образом

$I_{1}=E_{1}(u,v)\operatorname {d} u^{2}+2F_{1}(u,v)\operatorname {d} u\operatorname {d} v+G_{1}(u,v)\operatorname {d} v^{2}$

$I_{2}=E_{2}(u,v)\operatorname {d} u^{2}+2F_{2}(u,v)\operatorname {d} u\operatorname {d} v+G_{2}(u,v)\operatorname {d} v^{2}$

Условие конформного отображения двух поверхностей, сформулированное в дифференциальной геометрии, требует, чтобы

${\sqrt {I_{2}}}=\lambda {\sqrt {I_{1}}}$

где $\ \lambda$ — коэффициент искажения поверхности из-за конформного отображения.

Известно, что первая квадратичная форма отражает расстояние между двумя точками поверхности. $\ (u,v)$ и $\ (u+\operatorname {d} u,v+\operatorname {d} v)$. Когда $\ \lambda$-ratio близко к 1, приведенное выше уравнение сходится к условию изометрического отображения и к равноплощадному отображению соответственно из-за инвариантности углов между любыми кривыми и инвариантности любых участков площади. Помня, что первый этап поиска формы основан на треугольной сетке поверхности и используя метод взвешенных невязок для описания изометрического и равноплощадного отображения минимальной поверхности на плоскую область, мы можем написать следующую функцию, которая определяется суммой интегралов по отрезкам криволинейных треугольников

$\Pi =D\sum _{j=1}^{n}\oint _{S_{j}}w_{j}\left(\lambda {\sqrt {I_{1}}}-{\sqrt {I_{2}}}\right)^{2}\operatorname {d} s$

где

• $\ n$ - общее количество ячеек сетки,
• $\ w_{j}$ - весовые коэффициенты,
• $\ \Pi$ - общий остаток отображения,
• $\ D$ - константа, не влияющая на конечный результат и может использоваться в качестве масштабного коэффициента.

Учитывая дальнейшие весовые соотношения $\ w_{j}=1$ мы можем преобразовать уравнение. в приближенную конечную сумму, которая представляет собой комбинацию линейных расстояний между узлами поверхностной сетки, и запишите основное условие равноплощадного отображения поверхности как минимум следующей нелинейной функции

$\Pi =D\sum _{j=1}^{n}\oint _{S_{j}}w_{j}\left(\lambda R_{j}-L_{j}\right)^{2}\operatorname {d} s$

где

• $\ R_{j}$ - начальная длина номера линейного отрезка $\ j$,
• $\ L_{j}$ - конечная длина номера сегмента $\ j$,
• $\ \lambda$ - коэффициент искажений близок к 1 и может быть разным для каждого сегмента.

Начальная и конечная длина номера сегмента $\ j$ может быть выражено, как обычно, двумя узловыми координатами как

$R={\sqrt {(X_{12}-X_{11})^{2}+(X_{22}-X_{21})^{2}+(X_{32}-X_{31})^{2}}}$

$L={\sqrt {(x_{12}-x_{11})^{2}+(x_{22}-x_{21})^{2}}}$

где

• $\ X_{ik}$ - координаты узлов начального отрезка,
• $\ x_{ik}$ - координаты узлов конечного сегмента.

По исходному предположению можем написать $\ x_{32}=x_{31}=0$ для отображения плоской поверхности. Выражение для векторов $\{\ x\}$ и $\{\ X\}$ с приращением координат использование термина можно записать как

$\{\ x\}=\{\ X\}+\{\Delta \ X\}$

Рис. 9 Вырез двухпиковой маркизы

Рис. 10 Исходный вид патча

Рис. 11. Схема плоского патча.

Вектор $\{\Delta \ X\}$ определение производится так же, как и ранее

${\frac {\partial \Pi }{\partial \Delta X_{kl}}}=0$

После преобразований мы можем записать следующие две независимые системы нелинейных алгебраических уравнений:

$[\ A]\{\Delta X_{1}\}=\{\ B_{1}\}+\{\Delta P_{1}\}$

$[\ A]\{\Delta X_{2}\}=\{\ B_{2}\}+\{\Delta P_{2}\}$

где все части системы могут быть выражены, как ранее, и $\{\ \Delta P_{1}\}$ и $\{\ \Delta P_{2}\}$ — векторы псевдонапряжений в осях 1, 2, имеющие следующий вид

$\{\Delta P_{lt}\}=-\left\{\sum _{j=1}^{N}\lambda {\frac {R_{m}}{L_{m}}}(x_{lm}-x_{lt})\right\}$

где

• $\ N$ - общее количество узлов, окружающих номер узла $\ t$,
• $\ l$ - количество глобальных осей.

Описанный выше подход является другой формой SGM и позволяет получить две независимые системы нелинейных алгебраических уравнений, которые можно решить любой стандартной итерационной процедурой. Чем меньше гауссова кривизна поверхности, тем выше точность отображения плоскости. Как правило, плоскостное картографирование позволяет получить рисунок с линейными размерами на 1–2% меньшими, чем соответствующие пространственные линии конечной поверхности. Именно поэтому при нанесении рисунка необходимо предусмотреть соответствующие поля.

Типичный образец выреза, также называемый вырезом, выступом (сегментом) или заплаткой, представлен на рис. 9, 10, 11.

См. также

• Генерация сетки
• Виды сетки

Внешние ссылки

• Система К3-Тент для поиска формы и раскроя натяжных тканевых конструкций
• Кубантентская корпорация