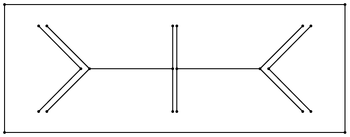
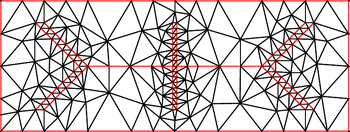
Уточнение Делоне
При создании сетки уточнения Делоне — это алгоритмы создания сетки, основанные на принципе добавления точек Штейнера к геометрии входных данных, которые должны быть объединены в сетку, таким образом, чтобы триангуляция Делоне или ограниченная триангуляция Делоне расширенных входных данных соответствовала требованиям качества. приложения для построения сетки. Методы уточнения Делоне включают методы Чу и Руперта.
Второй алгоритм Чу
[ редактировать ]
Второй алгоритм Чу использует кусочно-линейную систему (PLS) и возвращает ограниченную триангуляцию Делоне, состоящую только из качественных треугольников, где качество определяется минимальным углом в треугольнике. Разработан Л. Полом Чу для создания сетки поверхностей, встроенных в трехмерное пространство. [ 1 ] Второй алгоритм Чу был принят в качестве генератора двумерной сетки из-за практических преимуществ перед алгоритмом Руперта в определенных случаях и является генератором сетки качества по умолчанию, реализованным в свободно доступном пакете Triangle . [ 2 ] Второй алгоритм Чу гарантированно завершает работу и создает сетки с градуировкой по размеру локальных объектов с минимальным углом примерно до 28,6 градусов. [ 3 ]
Алгоритм начинается с ограниченной триангуляции Делоне входных вершин. На каждом шаге в триангуляцию вставляется центр описанной окружности треугольника низкого качества, за одним исключением: если центр описанной окружности лежит на стороне входного сегмента, противоположной стороне треугольника низкого качества, вставляется середина сегмента. Более того, все ранее вставленные центры окружностей внутри диаметрального шара исходного сегмента (до его разделения) удаляются из триангуляции. Вставка описанного центра повторяется до тех пор, пока не исчезнут некачественные треугольники.
Алгоритм Руперта
[ редактировать ]Алгоритм Руперта берет плоский прямолинейный граф (или в размерности больше двух - кусочно-линейную систему) и возвращает соответствующую триангуляцию Делоне, состоящую только из качественных треугольников. Треугольник считается некачественным, если его отношение радиуса описанной окружности к кратчайшему краю больше некоторого заданного порога. Обнаруженный Джимом Рупертом в начале 1990-х годов, [ 4 ] «Алгоритм Руперта для создания качественной двумерной сетки, возможно, является первым теоретически гарантированным алгоритмом построения сетки , который действительно удовлетворительен на практике». [ 5 ]
Мотивация
[ редактировать ]При выполнении компьютерного моделирования, такого как вычислительная гидродинамика , каждый начинает с такой модели, как 2D-контур секции крыла. Входные данные для двумерного метода конечных элементов должны быть в виде треугольников, заполняющих все пространство, и каждый треугольник должен быть заполнен одним типом материала – в данном примере «воздухом» или «крылом». Длинные, тонкие треугольники невозможно точно смоделировать. Время моделирования обычно пропорционально количеству треугольников, поэтому желательно минимизировать количество треугольников, при этом используя достаточное количество треугольников для получения достаточно точных результатов – обычно с использованием неструктурированной сетки . Компьютер использует алгоритм Руперта (или какой-либо аналогичный алгоритм построения сетки) для преобразования многоугольной модели в треугольники, подходящие для метода конечных элементов.
Алгоритм
[ редактировать ]Алгоритм начинается с триангуляции Делоне входных вершин, а затем состоит из двух основных операций.
- В триангуляцию вставляется середина отрезка с непустыми диаметральными окружностями.
- В триангуляцию вставляется центр описанной окружности некачественного треугольника, если только этот центр описанной окружности не лежит в диаметральной окружности какого-либо отрезка. В этом случае вместо этого разбивается захваченный сегмент.
Эти операции повторяются до тех пор, пока не останется некачественных треугольников и не будут захвачены все отрезки.
- Псевдокод
function Ruppert(points, segments, threshold) is
T := DelaunayTriangulation(points)
Q := the set of encroached segments and poor quality triangles
while Q is not empty: // The main loop
if Q contains a segment s:
insert the midpoint of s into T
else Q contains poor quality triangle t:
if the circumcenter of t encroaches a segment s:
add s to Q;
else:
insert the circumcenter of t into T
end if
end if
update Q
end while
return T
end Ruppert.
Практическое использование
[ редактировать ]Без модификации алгоритм Руперта гарантированно завершит работу и сгенерирует качественную сетку для неострых входных сигналов и любого порога низкого качества менее 20,7 градусов. Чтобы ослабить эти ограничения, были внесены различные небольшие улучшения. Ослабив требования к качеству вблизи малых входных углов, алгоритм можно расширить для обработки любого прямолинейного входного сигнала. [ 6 ] Кривые входные данные также можно создать сетку, используя аналогичные методы. [ 7 ] Алгоритм Руперта может быть естественным образом расширен до трехмерности, однако его гарантии вывода несколько слабее из-за тетраэдра ленточного типа.
Расширение алгоритма Руперта в двух измерениях реализовано в свободно доступном пакете Triangle . Два варианта алгоритма Руперта в этом пакете гарантированно завершаются при пороге низкого качества около 26,5 градусов. [ 8 ] На практике эти алгоритмы успешны для некачественных порогов более 30 градусов. Однако известны примеры, приводящие к сбою алгоритма при пороге больше 29,06 градуса. [ 9 ]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Чу, Л. Пол (1993). «Гарантированное качество создания сетки для криволинейных поверхностей». Материалы девятого ежегодного симпозиума по вычислительной геометрии . стр. 274–280.
- ^ Шевчук, Джонатан (2002). «Алгоритмы уточнения Делоне для построения треугольной сетки» . Вычислительная геометрия: теория и приложения . 22 (1–3): 21–74. дои : 10.1016/s0925-7721(01)00047-5 .
- ^ Рэнд, Александр (2011). «Где и как работает второй алгоритм уточнения Делоне Чу» (PDF) . Материалы 23-й канадской конференции по вычислительной геометрии . стр. 157–162.
- ^ Руперт, Джим (1995). «Алгоритм уточнения Делоне для создания качественной двумерной сетки». Журнал алгоритмов . 18 (3): 548–585. дои : 10.1006/jagm.1995.1021 .
- ^ Шевчук, Джонатан (12 августа 1996 г.). «Алгоритм уточнения Делоне Руперта» . Проверено 28 декабря 2018 г.
- ^ Миллер, Гэри; Пав, Стивен; Уокингтон, Ноэль (2005). «Когда и почему работают алгоритмы уточнения Делоне». Международный журнал вычислительной геометрии и приложений . 15 (1): 25–54. дои : 10.1142/S0218195905001592 .
- ^ Пав, Стивен; Уокингтон, Ноэль (2005). Уточнение Делоне за счет обрезки углов . Материалы 14-го Международного круглого стола по сетке. стр. 165–181.
- ^ Шевчук, Джонатан (2002). «Алгоритмы уточнения Делоне для построения треугольной сетки» . Вычислительная геометрия: теория и приложения . 22 (1–3): 21–74. дои : 10.1016/s0925-7721(01)00047-5 .
- ^ Рэнд, Александр (2011). «Улучшенные примеры незавершения алгоритма Руперта». arXiv : 1103.3903 [ cs.CG ]. .
Дальнейшее чтение
[ редактировать ]- Рино, Лоран. «2D-согласованные триангуляции и сетки» . Проверено 28 декабря 2018 г.
- Шевчук, Джонатан. «Треугольник: двумерный генератор качественной сетки и триангулятор Делоне» . Проверено 28 декабря 2018 г.
- Си, Ханг (2015). «TetGen: качественный генератор тетраэдральной сетки и 3D-триангулятор Делоне» . Архивировано из оригинала 29 декабря 2018 года . Проверено 28 декабря 2018 г.
{{cite web}}: CS1 maint: bot: исходный статус URL неизвестен ( ссылка )