Диэдр
| Набор правильных n- угольных диэдров | |
|---|---|
 Пример шестиугольного двугранника на сфере | |
| Тип | правильный многогранник или сферическая мозаика |
| Лица | 2 н - кайф |
| Края | н |
| Вершины | н |
| Конфигурация вершин | н . н |
| Символ Витхоффа | 2 | № 2 |
| Символ Шлефли | { н , 2} |
| Диаграмма Кокстера | |
| Группа симметрии | D n h , [2, n ], (*22 n ), порядок 4 n |
| Группа ротации | Д н , [2, н ] + , (22 n ), порядок 2 n |
| Двойной многогранник | правильный n -угольный осоэдр |
Диэдр — это разновидность многогранника , состоящего из двух граней многоугольника , имеющих один и тот же набор из n ребер . В трехмерном евклидовом пространстве он вырожден , если его грани плоские, тогда как в трехмерном сферическом пространстве двугранник с плоскими гранями можно рассматривать как линзу, примером которой является фундаментальная область линзового пространства L. ( п , q ). [1] Диэдры также называли биэдрами . [2] плоские многогранники , [3] или дважды покрытые многоугольники . [3]
Как сферическая мозаика , диэдр может существовать в виде невырожденной формы с двумя n -сторонними гранями, покрывающими сферу, причем каждая грань представляет собой полусферу , а вершины находятся на большом круге . Оно правильное, если вершины расположены на одинаковом расстоянии друг от друга.
Двойственным к -угольному диэдру n является n -угольный осоэдр , в котором n двуугольных граней имеют общие две вершины.
В виде плоскогранного многогранника
[ редактировать ]Диэдр два можно рассматривать как вырожденную призму, (плоских) n -сторонних основания многоугольника которой соединены «спина к спине», так что образующийся объект не имеет глубины. Полигоны должны быть конгруэнтны, но склеены таким образом, чтобы один был зеркальным отражением другого. Это применимо только в том случае, если расстояние между двумя гранями равно нулю; на расстоянии больше нуля грани представляют собой бесконечные многоугольники (немного похоже на двуугольные грани апейрогонального осоэдра , имеющие ширину больше нуля и представляющие собой бесконечные полосы).
Диэдры могут возникнуть из теоремы единственности Александрова , которая характеризует расстояния на поверхности любого выпуклого многогранника как локально евклидовы, за исключением конечного числа точек с положительным угловым дефектом , сумма которых равна 4 π . Эта характеристика справедлива и для расстояний на поверхности двугранника, поэтому утверждение теоремы Александрова требует, чтобы диэдры рассматривались как выпуклые многогранники. [4]
Некоторые двугранники могут возникать как члены нижнего предела других семейств многогранников: призма с двуугольными основаниями будет квадратным двугранником, а пирамида с двуугольным основанием будет треугольным двугранником.
Правильный диэдр с символом Шлефли { n ,2} состоит из двух правильных многоугольников , каждый из которых имеет символ Шлефли { n }. [5]
Как замощение сферы
[ редактировать ]Сферический диэдр состоит из двух сферических многоугольников , имеющих один и тот же набор из n вершин, на большого круга экваторе ; каждый многоугольник сферического диэдра заполняет полусферу .
Правильный сферический диэдр состоит из двух правильных сферических многоугольников, которые имеют один и тот же набор из n вершин, равномерно расположенных по экватору большого круга .
Правильный многогранник {2,2} самодуален и является одновременно осоэдром и диэдром.
| Космос | сферический | евклидов | |||||
|---|---|---|---|---|---|---|---|
| Укладка плитки имя | моногональный двугранник | Дигональный двугранник | Треугольный двугранник | Квадрат двугранник | пятиугольный двугранник | ... | Апейрогональный двугранник |
| Укладка плитки изображение | 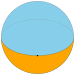 |  |  | 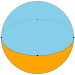 | 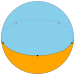 | ... | |
| Шлефли символ | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | ... | {∞,2} |
| Коксетер диаграмма | ... | ||||||
| Лица | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | ... | 2 {∞} |
| Края и вершины | 1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Вертекс конфиг. | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | ... | ∞.∞ |
Апейрогональный диэдр
[ редактировать ]Когда n стремится к бесконечности, n -угольный диэдр становится апейрогональным диэдром как двумерная мозаика: 
Дитопы
[ редактировать ]Правильный дитоп — это n- мерный аналог диэдра с символом Шлефли { p ,..., q , r ,2}. Он имеет две грани , { p ,..., q , r }, которые имеют все ребра , { p ,..., q }. общие [6]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Гаусманн, Эвелиза; Роланд Леук; Жан-Пьер Люмине; Жан-Филипп Узан; Джеффри Уикс (2001). «Топологическое линзирование в сферических пространствах». Классическая и квантовая гравитация . 18 (23): 5155–5186. arXiv : gr-qc/0106033 . Бибкод : 2001CQGra..18.5155G . дои : 10.1088/0264-9381/18/23/311 . S2CID 34259877 .
- ^ Кантор, С. (2003), «Об объеме неограниченных многогранников в гиперболическом пространстве» (PDF) , Beiträge zur Algebra und Geometrie , 44 (1): 145–154, MR 1990989 , заархивировано из оригинала (PDF) на 15 февраля 2017 г. , получено 14 февраля 2017 г.
- ^ Jump up to: а б О'Рурк, Джозеф (2010), Пары плоская молния-раскладывание для платоновых тел , arXiv : 1010.2450 , Bibcode : 2010arXiv1010.2450O
- ^ О'Рурк, Джозеф (2010), О плоских многогранниках, вытекающих из теоремы Александрова , arXiv : 1007.2016 , Bibcode : 2010arXiv1007.2016O
- ^ Коксетер, HSM (январь 1973 г.), Правильные многогранники (3-е изд.), Dover Publications Inc., стр. 12 , ISBN 0-486-61480-8
- ^ МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , стр. 158 , ISBN 0-521-81496-0