Ячейка Вигнера – Зейтца

Ячейка Вигнера-Зейтца , названная в честь Юджина Вигнера и Фредерика Зейтца , представляет собой примитивную ячейку , которая была построена путем применения разложения Вороного к кристаллической решетке . Его используют при изучении кристаллических материалов в кристаллографии .

Примитивная ячейка Вигнера – Зейтца для решеток параллелограммов с разными углами.

Уникальное свойство кристалла состоит в том, что его атомы расположены в правильном трехмерном массиве, называемом решеткой . Все свойства, приписываемые кристаллическим материалам, обусловлены этой высокоупорядоченной структурой. Такая структура обладает дискретной трансляционной симметрией . Чтобы смоделировать и изучить такую ​​периодическую систему, нужна математическая «ручка», чтобы описать симметрию и, следовательно, сделать выводы о свойствах материала, вытекающих из этой симметрии. Ячейка Вигнера-Зейтца является средством достижения этой цели.

Ячейка Вигнера-Зейтца является примером примитивной ячейки , которая представляет собой элементарную ячейку, содержащую ровно одну точку решетки. Для любой данной решетки существует бесконечное количество возможных примитивных ячеек. Однако для любой данной решетки существует только одна ячейка Вигнера – Зейтца. Это место точек в пространстве, которые находятся ближе к этой точке решетки, чем к любой другой точке решетки.

Ячейка Вигнера-Зейтца, как и любая примитивная ячейка, является фундаментальной областью дискретной трансляционной симметрии решетки. Примитивная ячейка обратной решетки в импульсном пространстве называется зоной Бриллюэна .

Обзор

Фон

Концепция разложения Вороного была исследована Питером Густавом Леженом Дирихле , что привело к названию области Дирихле . Дальнейшие материалы были сделаны Евграфом Федоровым , ( Параллелоэдр Федорова ), Георгием Вороным ( Многогранник Вороного ), и Пол Ниггли ( область ).

Применение к физике конденсированного состояния было впервые предложено Юджином Вигнером и Фредериком Зейтцем в статье 1933 года, где оно использовалось для решения уравнения Шредингера для свободных электронов в элементарном натрии . Они аппроксимировали форму ячейки Вигнера-Зейтца в натрии, которая представляет собой усеченный октаэдр, как сферу равного объема, и решили уравнение Шредингера точно, используя периодические граничные условия , которые требуют $d\psi /dr=0$ на поверхности сферы. Аналогичный расчет, который также учитывал несферическую природу ячейки Вигнера-Зейтца, был выполнен позже Джоном К. Слейтером .

Существует только пять топологически различных многогранников, которые замощают трехмерное пространство , ℝ ³ . Их называют параллелоэдрами . Они являются предметом математического интереса, например, в высших измерениях. Эти пять параллелоэдров можно использовать для классификации трехмерных решеток с использованием концепции проективной плоскости, предложенной Джоном Хортоном Конвеем и Нилом Слоаном . Однако, в то время как топологическая классификация считает, что любое аффинное преобразование приводит к идентичному классу, более конкретная классификация приводит к 24 различным классам многогранников Вороного с параллельными ребрами, которые замостили пространство. Например, прямоугольный кубоид , прямоугольная призма и куб принадлежат к одному топологическому классу, но отличаются разными соотношениями своих сторон. Эта классификация 24 типов многогранников Вороного для решеток Браве была впервые изложена Борисом Делоне .

Определение

Ячейка Вигнера-Зейтца вокруг точки решетки определяется как геометрическое место точек в пространстве, которые находятся ближе к этой точке решетки, чем к любой другой точке решетки.

Математически можно показать, что ячейка Вигнера-Зейтца является примитивной клеткой . Это означает, что ячейка охватывает все прямое пространство, не оставляя зазоров или дыр — свойство, известное как тесселяция .

Построение клетки

Построение примитивной ячейки Вигнера–Зейтца.

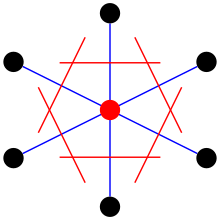
Общая математическая концепция, воплощенная в ячейке Вигнера-Зейтца, чаще называется ячейкой Вороного , а разбиение плоскости на эти ячейки для заданного набора точечных узлов известно как диаграмма Вороного .

Процесс построения ячейки Вигнера – Зейтца гексагональной решетки.

Ячейку можно выбрать, сначала выбрав точку решетки . После выбора точки ко всем близлежащим точкам решетки рисуются линии. В средней точке каждой линии рисуется еще одна линия, перпендикулярная каждому из первого набора линий. Наименьшая область, заключенная таким образом, называется примитивной ячейкой Вигнера-Зейтца .

Для трехмерной решетки шаги аналогичны, но на шаге 2 вместо рисования перпендикулярных линий в середине линий между точками решетки рисуются перпендикулярные плоскости.

Как и в случае со всеми примитивными ячейками, вся область или пространство внутри решетки может быть заполнено ячейками Вигнера – Зейтца, и пробелов не будет.

Соседние точки решетки постоянно проверяются до тех пор, пока заключенная в них площадь или объем не станет подходящей площадью или объемом для примитивной ячейки . Альтернативно, если базисные векторы решетки сокращаются с использованием сокращения решетки, необходимо использовать только заданное количество точек решетки. В двумерных измерениях необходимо использовать только точки решетки, составляющие 4 элементарные ячейки, имеющие общую вершину с началом координат. В трехмерных измерениях необходимо использовать только точки решетки, составляющие 8 элементарных ячеек, имеющих общую вершину с началом координат.

Ячейка Вигнера-Зейтца примитивной кубической решетки представляет собой куб . В математике она известна как кубические соты .

Ячейка Вигнера-Зейтца объемноцентрированной кубической решетки представляет собой усеченный октаэдр . В математике она известна как усеченная кубическая сота .

Ячейка Вигнера-Зейтца гранецентрированной кубической решетки представляет собой ромбдодекаэдр . В математике он известен как ромбдодекаэдрические соты .

Ячейка Вигнера – Зейтца объемноцентрированной тетрагональной решетки, постоянная решетки которой равна $c/a>{\sqrt {2}}$ представляет собой вытянутый додекаэдр .

Ячейка Вигнера-Зейтца примитивной гексагональной решетки представляет собой шестиугольную призму . В математике он известен как шестиугольные призматические соты .

Форма ячейки Вигнера–Зейтца для любой решетки Браве принимает форму одного из 24 многогранников Вороного. Чтобы указать дополнительные ограничения, $a,b,c,\alpha ,\beta$ – параметры элементарной ячейки, а ${\vec {a}}_{1},{\vec {a}}_{2},{\vec {a}}_{3},{\vec {a}}_{4}$ являются базисными векторами.

		Топологический класс (аффинный эквивалентный параллелоэдр )
		Усеченный октаэдр	Вытянутый додекаэдр	Ромбический додекаэдр	Шестиугольная призма	Куб
Решетка Браве	Примитивная кубическая					Любой
	Гранецентрированный кубический			Любой
	Телоцентрированная кубическая	Любой
	Примитивный шестиугольный				Любой
	Примитивный ромбоэдрический	$\alpha >90^{\circ }$		$\alpha <90^{\circ }$
	Примитивный четырехугольный					Любой
	Телоцентрированный тетрагональный	$c/a<{\sqrt {2}}$	$c/a>{\sqrt {2}}$
	Примитивный орторомбический					Любой
	Орторомбический с центром в основании				Любой
	Гранецентрированный орторомбический	Любой
	Телоцентрированный орторомбический	$c^{2}<a^{2}+b^{2}$	$c^{2}>a^{2}+b^{2}$	$c^{2}=a^{2}+b^{2}$
	Примитивная моноклиника				Любой
	Базово-центровая моноклиника	$a<b$	$a>b$, $a^{2}-b^{2}>2ac\cos \beta$	$a>b$, $a^{2}-b^{2}=2ac\cos \beta$
		$a>b$, $a^{2}-b^{2}<2ac\cos \beta$	$a=b$
	Примитивная триклиника	${\vec {a}}_{i}\cdot {\vec {a}}_{j}\neq 0$ $i,j\in \{1,2,3,4\}$ где $i\neq j$	${\vec {a}}_{i}\cdot {\vec {a}}_{j}=0$ один раз	${\vec {a}}_{i}\cdot {\vec {a}}_{j}=0={\vec {a}}_{k}\cdot {\vec {a}}_{l}$ $i,j,k,l\in \{1,2,3,4\}$ где $i\neq j\neq k\neq l$

Композитные решетки

Для составных решеток (кристаллов, которые имеют более одного вектора в основе ) каждая отдельная точка решетки представляет несколько атомов. Мы можем разбить каждую ячейку Вигнера-Зейтца на подячейки путем дальнейшего разложения Вороного по ближайшему атому, а не по ближайшему узлу решетки. Например, кристаллическая структура алмаза содержит двухатомную основу. В алмазе атомы углерода имеют тетраэдрическую форму sp. ³ Связывание , но поскольку тетраэдры не образуют мозаичное пространство , вороное разложение кристаллической структуры алмаза на самом деле представляет собой усеченные триаки тетраэдрические соты . Другой пример — применение разложения Вороного к атомам в фазах A15 , которое образует полиэдрическое приближение структуры Вейра-Фелана .

Симметрия

Ячейка Вигнера-Зейтца всегда имеет ту же точечную симметрию , что и лежащая в основе решетка Браве . Например, куб , усеченный октаэдр и ромбический додекаэдр имеют точечную симметрию Oh _, поскольку все соответствующие решетки Браве, использованные для их создания, принадлежат системе кубических решеток , которая имеет _{точечную симметрию Oh} .

Зона Бриллюэна

Основная статья: Зона Бриллюэна

На практике сама ячейка Вигнера-Зейтца на самом деле редко используется для описания прямого пространства обычные элементарные ячейки , вместо нее обычно используются . Однако то же самое разложение чрезвычайно важно применительно к обратному пространству . Ячейка Вигнера-Зейтца в обратном пространстве называется зоной Бриллюэна и содержит информацию о том, будет ли материал проводником , полупроводником или изолятором .

См. также

• Триангуляция Делоне
• Координационная геометрия
• Теория кристаллического поля
• Вигнер кристалл