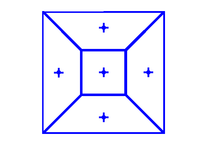
Центроидальная мозаика Вороного
В геометрии центроидальная мозаика Вороного ( CVT ) — это особый тип мозаики Вороного , в котором образующая точка каждой ячейки Вороного также является ее центроидом (центром масс). Его можно рассматривать как оптимальное разбиение, соответствующее оптимальному распределению образующих. Для создания центроидальных тесселяций Вороного можно использовать ряд алгоритмов, включая алгоритм Ллойда для кластеризации K-средних или квазиньютоновские методы, такие как BFGS . [1]
Доказательства
[ редактировать ]Гипотеза Гершо, доказанная для одного и двух измерений, гласит, что «асимптотически говоря, все ячейки оптимального CVT, образуя мозаику , конгруэнтны базовой ячейке, которая зависит от измерения». [2]
В двух измерениях базовой ячейкой оптимального CVT является правильный шестиугольник , поскольку доказано, что он представляет собой наиболее плотную упаковку кругов в двумерном евклидовом пространстве.Его трехмерный эквивалент — ромбические додекаэдрические соты , возникшие в результате наиболее плотной упаковки сфер в трехмерном евклидовом пространстве.
Приложения
[ редактировать ]Центроидальные тесселяции Вороного полезны при сжатии данных , оптимальной квадратуре , оптимальном квантовании , кластеризации и создании оптимальной сетки. [3]
Взвешенные центроидальные диаграммы Вороного представляют собой вариатор, в котором каждый центроид взвешивается в соответствии с определенной функцией. Например, изображение в оттенках серого можно использовать как функцию плотности для взвешивания точек CVT, как способ создания цифровой пунктирности . [4]
Встречаемость в природе
[ редактировать ]Многие закономерности, наблюдаемые в природе, очень похожи на центроидальную мозаику Вороного. Примеры этого включают Дорогу Гигантов , клетки роговицы , [5] и ямы для размножения самцов тилапии . [3]
Ссылки
[ редактировать ]- ^ Носедаль, Хорхе; Райт, Стивен Дж. (2006). Численная оптимизация . Серия Springer по исследованию операций и финансовой инженерии (второе изд.). Спрингер. дои : 10.1007/978-0-387-40065-5 . ISBN 978-0-387-30303-1 .
- ^ Ду, Цян; Ван, Дешенг (2005), «Оптимальные центроидальные мозаики Вороного и гипотеза Гершо в трехмерном пространстве», Компьютеры и математика с приложениями , 49 (9–10): 1355–1373, doi : 10.1016/j.camwa. 2004.12.008
- ^ Jump up to: а б Ду, Цян; Фабер, Вэнс ; Гинцбургер, Макс (1999), «Центроидальные тесселяции Вороного: приложения и алгоритмы», SIAM Review , 41 (4): 637–676, Bibcode : 1999SIAMR..41..637D , CiteSeerX 10.1.1.452.2448 , doi : 10.1137/ S0036144599352836 .
- ^ Секорд, Адриан. «Взвешенная вороная пунктирность». Материалы 2-го международного симпозиума по нефотореалистичной анимации и рендерингу. АКМ, 2002.
- ^ Пигатто, Жоао Антонио Тадеу; и др. (2009). «Сканирующая электронная микроскопия эндотелия роговицы страуса» . наук. Деревенский . 39 (3): 926–929. дои : 10.1590/S0103-84782009005000001 . hdl : 11449/29422 .