Пятиугольник

Правильный пятиугольник
Правильный пятиугольник
	Правильный пятиугольник
Тип	Правильный многоугольник
Ребра и вершины	15
Символ Шлефли	{15}
Диаграммы Кокстера – Дынкина
Группа симметрии	Двугранник (Д 15 ), заказ 2×15
Внутренний угол ( градусы )	156°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии пятиугольник или 15-угольник — или пентакаидекагон это пятнадцатисторонний многоугольник .

Правильный пятиугольник [ править ]

Правильный . пятиугольник представлен символом Шлефли {15}

Правильный ° углы 156 пятиугольник имеет внутренние , а при длине стороны a его площадь равна

{\begin{aligned}A={\frac {15}{4}}a^{2}\cot {\frac {\pi }{15}}&={\frac {15}{4}}{\sqrt {7+2{\sqrt {5}}+2{\sqrt {15+6{\sqrt {5}}}}}}a^{2}\\&={\frac {15a^{2}}{8}}\left({\sqrt {3}}+{\sqrt {15}}+{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}\right)\\&\simeq 17.6424\,a^{2}.\end{aligned}}

Строительство [ править ]

Поскольку 15 = 3 × 5, произведение различных простых чисел Ферма , правильный пятидесятиугольник можно построить с помощью циркуля и линейки : Следующие конструкции правильных пятидесятиугольников с заданной описанной окружностью аналогичны иллюстрации предложения XVI в книге IV « Евклида Начал» . ^[1]

Сравните построение по Евклиду на этом изображении: Пятиугольник.

В построении для данной описанной окружности: ${\overline {FG}}={\overline {CF}}{\text{,}}\;{\overline {AH}}={\overline {GM}}{\text{,}}\;|E_{1}E_{6}|$ является стороной равностороннего треугольника и $|E_{2}E_{5}|$ является стороной правильного пятиугольника. ^[2]Суть $H$ делит радиус ${\overline {AM}}$ в золотом сечении : ${\frac {\overline {AH}}{\overline {HM}}}={\frac {\overline {AM}}{\overline {AH}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}$

По сравнению с первой анимацией (с зелеными линиями) на следующих двух изображениях показаны две круговые дуги (для углов 36 ° и 24 °), повернутые на 90 ° против часовой стрелки. Они не используют сегмент ${\overline {CG}}$ , а скорее используют сегмент ${\overline {MG}}$ как радиус ${\overline {AH}}$ для второй дуги окружности (угол 36°).

Конструкция циркуля и линейки для заданной длины стороны. Конструкция почти равна конструкции пятиугольника с заданной стороной , тогда представление также завершается расширением одной стороны и генерирует сегмент, здесь ${\overline {FE_{2}}}{\text{,}}$ который делится по золотому сечению:

${\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}$

Окружность ${\overline {E_{2}M}}=R\;;\;\;$ Длина стороны ${\overline {E_{1}E_{2}}}=a\;;\;\;$ Угол $DE_{1}M=ME_{2}D=78^{\circ }$

${\begin{aligned}R&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)={\frac {1}{2}}\cdot {\sqrt {8+2\cdot {\sqrt {5}}+2{\sqrt {15+6\cdot {\sqrt {5}}}}}}\cdot a\\&={\frac {\sin(78^{\circ })}{\sin(24^{\circ })}}\cdot a\approx 2.40486\cdot a\end{aligned}}$

Конструкция для заданной длины стороны

Построение по заданной длине стороны в виде анимации,

{\overline {E_{2}M}}={\overline {CG}}

Симметрия [ править ]

Правильный пятиугольник имеет _{Dih 15} двугранную симметрию , порядка 30, представленную 15 линиями отражения. Dih ₁₅ имеет 3 двугранные подгруппы: Dih ₅ , Dih ₃ и Dih ₁ . И еще четыре циклические симметрии: Z ₁₅ , Z ₅ , Z ₃ и Z ₁ , где Z _n представляет π/ n радианную вращательную симметрию .

В пятидесятиугольнике имеется 8 различных симметрий. Джон Конвей обозначает эти симметрии буквой, а порядок симметрии следует за буквой. ^[3] Он дает r30 для полной отражательной симметрии, Dih ₁₅ . Он дает d (диагональ) с линиями отражения через вершины, p с линиями отражения через края (перпендикулярно) и для нечетного пятиугольника i с зеркальными линиями, проходящими как через вершины, так и через края, и g для циклической симметрии. a1 обозначает отсутствие симметрии.

Эти более низкие симметрии допускают степень свободы в определении неправильных пятиугольников. Только подгруппа g15 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Пентадекаграммы [ править ]

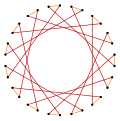
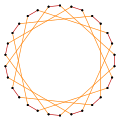
Существует три правильных звездчатых многоугольника : {15/2}, {15/4}, {15/7}, построенных из одних и тех же 15 вершин правильного пятиугольника, но соединенных пропуском каждой второй, четвертой или седьмой вершины соответственно.

Есть также три правильные звездные фигуры : {15/3}, {15/5}, {15/6}, первая из которых представляет собой соединение трех пятиугольников , вторая - соединение пяти равносторонних треугольников , а третья - соединение трех равносторонних треугольников. три пентаграммы .

Составную фигуру {15/3} можно рассматривать как двумерный эквивалент трехмерного соединения пяти тетраэдров .

Картина	{15/2}	{15/3} или 3{5}	{15/4}	{15/5} или 5{3}	{15/6} или 3{5/2}	{15/7}
Внутренний угол	132°	108°	84°	60°	36°	12°

Изогональные пятидесятиугольники [ править ]

Более глубокие усечения правильного пятиугольника и пентадекаграмм могут привести к образованию изогональных ( вершинно-транзитивных ) промежуточных звездчатых многоугольников с равными интервалами между вершинами и двумя длинами ребер. ^[4]

Вершинно-транзитивные усечения пятиугольника
Quasiregular	Isogonal	Quasiregular
t{15/2}={30/2}		t{15/13}={30/13}
t{15/7} = {30/7}		t{15/8}={30/8}
t{15/11}={30/22}		t{15/4}={30/4}

Полигоны Петри [ править ]

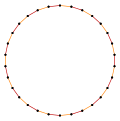
Правильный пятиугольник — это многоугольник Петри для некоторых многогранников более высокой размерности, спроецированный в косую ортогональную проекцию :

14-симплекс (14D)

Использует [ править ]

Правильный треугольник, десятиугольник и пятиугольник могут полностью заполнить вершину плоскости . Однако из-за нечетного числа сторон треугольника фигуры не могут чередоваться вокруг треугольника, поэтому вершина не может образовывать полуправильную мозаику .

См. также [ править ]

Ссылки [ править ]

^ Данэм, Уильям (1991). Путешествие через гения - Великие теоремы математики (PDF) . Пингвин. п. 65 . Получено 12 ноября 2015 г. - через Математический колледж искусств и наук Университета Кентукки.
^ Кеплер, Иоганнес, переведен и инициирован МАКСОМ КАСПАРОМ, 1939 г. WELT-HARMONIK (на немецком языке). п. 44 . Проверено 7 декабря 2015 г. - через Google Книги. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ) Получено 5 июня 2017 г.
^ Джон Х. Конвей , Хайди Бургель , Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
^ Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории (1994), Метаморфозы многоугольников , Бранко Грюнбаум

Внешние ссылки [ править ]

Вайсштейн, Эрик В. «Пентадекагон» . Математический мир .

[1] Данэм, Уильям (1991). Путешествие через гения - Великие теоремы математики (PDF) . Пингвин. п. 65 . Получено 12 ноября 2015 г. - через Математический колледж искусств и наук Университета Кентукки.

[2] Кеплер, Иоганнес, переведен и инициирован МАКСОМ КАСПАРОМ, 1939 г. WELT-HARMONIK (на немецком языке). п. 44 . Проверено 7 декабря 2015 г. - через Google Книги. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ) Получено 5 июня 2017 г.

[3] Джон Х. Конвей , Хайди Бургель , Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)

[4] Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории (1994), Метаморфозы многоугольников , Бранко Грюнбаум

[1]

[2]

[3]

[4]