Вытянутая пирамида
| Вытянутая пирамида | |
|---|---|
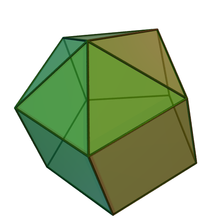 Пример: пятиугольная форма | |
| Лица | n треугольников n квадратов 1 н -гон |
| Края | 4 n |
| Вершины | 2н 1 + |
| Группа симметрии | C nv , [ n ], ( nn * |
| Группа вращения | С н , [ н ] + , ( нн ) |
| Двойной многогранник | самодвойственный |
| Характеристики | выпуклый |
В геометрии представляют вытянутые пирамиды собой бесконечное множество многогранников , построенных путем присоединения n -угольной пирамиды к n -угольной призме . Наряду с множеством пирамид эти фигуры топологически самодвойственны .
Есть три вытянутые пирамиды , которые являются твердыми телами Джонсона :
- Вытянутая треугольная пирамида ( J 7 ),
- Вытянутая квадратная пирамида ( J 8 ) и
- Вытянутая пятиугольная пирамида ( J 9 ).
Высшие формы можно построить с помощью равнобедренных треугольников .
Формы
[ редактировать ]| имя | лица | |
|---|---|---|
 | вытянутая треугольная пирамида ( J7 ) | 3+1 треугольника, 3 квадрата |
 | вытянутая квадратная пирамида ( J8 ) | 4 треугольника, 4+1 квадрата |
 | вытянутая пятиугольная пирамида ( J9 ) | 5 треугольников, 5 квадратов, 1 пятиугольник. |
См. также
[ редактировать ]Ссылки
[ редактировать ]- Норман В. Джонсон , «Выпуклые тела с правильными гранями», Canadian Journal of Mathematics, 18 , 1966, страницы 169–200. Содержит исходное перечисление 92 тел и гипотезу об отсутствии других.
- Виктор А. Залгаллер (1969). Выпуклые многогранники с правильными гранями . Консультантское бюро. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |