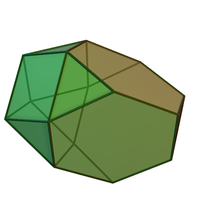
Дополненный усеченный тетраэдр
| Дополненный усеченный тетраэдр | |
|---|---|
 | |
| Тип | Джонсон Я 64 – Я 65 – Я 66 |
| Лица | 12 треугольников 3 квадрата 3 шестиугольника |
| Края | 27 |
| Вершины | 15 |
| Конфигурация вершин | 2x3(3,6 2 ) 3(3.4.3.4) 6(3.4.3.6) |
| Группа симметрии | С 3В |
| Характеристики | выпуклый |
| Сеть | |
 | |
В геометрии расширенный усеченный тетраэдр — многогранник, построенный путем присоединения треугольного купола к усеченному тетраэдру . Это пример твердого тела Джонсона .
Строительство
[ редактировать ]Расширенный усеченный тетраэдр создается из усеченного тетраэдра путем присоединения треугольного купола . [1] Этот купол закрывает шестиугольную грань так, что полученный многогранник имеет грани двенадцати равносторонних треугольников , трёх квадратов и трёх правильных шестиугольников . [2] обладает свойством выпуклости и имеет правильные многоугольные Поскольку расширенный усеченный тетраэдр грани, он представляет собой тело Джонсона , обозначаемое как шестьдесят пятое тело Джонсона. . [3]
Характеристики
[ редактировать ]Площадь поверхности расширенного усеченного тетраэдра равна: [2] сумма площадей его многоугольной грани. Его объем можно вычислить, разрезав его на усеченный тетраэдр и треугольный купол и сложив их объем: [2]
Он имеет ту же трехмерную группу симметрии, что и треугольный купол, пирамидальную симметрию. . Его двугранный угол можно получить, сложив угол треугольного купола и увеличенного усеченного тетраэдра следующим образом: [4]
- его двугранный угол между треугольником и шестиугольником равен углу усеченного тетраэдра между ними: 109,47°;
- его двугранный угол между соседними шестиугольниками равен углу усеченного тетраэдра между ними: 70,53°;
- его двугранный угол между треугольником и квадратом равен углу треугольного купола между ним: 125,3 °.
- его двугранный угол между треугольником и квадратом на краю, где прикреплены как треугольный купол, так и усеченный тетраэдр, представляет собой сумму угла как треугольного купола между квадратом и шестиугольником, так и угла усеченного тетраэдра между треугольником и шестиугольником: примерно 164,17. °; и
- его двугранный угол между треугольником и шестиугольником на краю, где прикреплены как треугольный купол, так и усеченный тетраэдр, представляет собой сумму двугранного угла треугольного купола и усеченного тетраэдра между ними: примерно 141,3 °;
Ссылки
[ редактировать ]- ^ Раджваде, Арканзас (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта . Тексты и чтения по математике. Книжное агентство Индостан. п. 84–89. дои : 10.1007/978-93-86279-06-4 . ISBN 978-93-86279-06-4 .
- ^ Jump up to: Перейти обратно: а б с Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .
- ^ Фрэнсис, Дэррил (август 2013 г.). «Твердые тела Джонсона и их сокращения» . Словесные пути . 46 (3): 177.
- ^ Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. , « Расширенный усеченный тетраэдр » (« Тело Джонсона ») в MathWorld .
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |