Перевернутый курносый додекадодекаэдр

Перевернутый курносый додекадодекаэдр

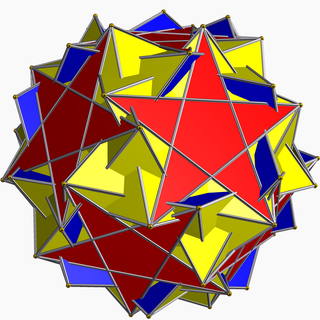Тип	Однородный звездчатый многогранник
Элементы	Ф = 84, Е = 150 V = 60 (χ = −6)
Лица по сторонам	60{3}+12{5}+12{5/2}
Диаграмма Кокстера
Символ Витхоффа	\| 5/3 2 5
Группа симметрии	Я, [5,3] ⁺, 532
Ссылки на индексы	Ю ₆₀ , С ₇₆ , Ж ₁₁₄
Двойной многогранник	Медиальный перевернутый пятиугольный шестиконтаэдр
Вершинная фигура	3.3.5.3.5/3
Аббревиатура Бауэрса	сделал

В геометрии перевернутый курносый додекадодекаэдр (или вертисноб додекадодекаэдр ) представляет собой невыпуклый однородный многогранник , обозначаемый как U ₆₀ . ^[1] Ему дан символ Шлефли $sr{5/3,5}.$

Декартовы координаты

Позволять $\xi \approx 2.109759446579943$ быть наибольшим действительным нулем многочлена $P=2x^{4}-5x^{3}+3x+1$ . Обозначим через $\phi$ золотое сечение . Пусть точка $p$ быть предоставлено

p={\begin{pmatrix}\phi ^{-2}\xi ^{2}-\phi ^{-2}\xi +\phi ^{-1}\\-\phi ^{2}\xi ^{2}+\phi ^{2}\xi +\phi \\\xi ^{2}+\xi \end{pmatrix}}

.

Пусть матрица $M$ быть предоставлено

M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}

.

$M$ это вращение вокруг оси $(1,0,\phi )$ под углом $2\pi /5$ , против часовой стрелки. Пусть линейные преобразования $T_{0},\ldots ,T_{11}$ быть преобразованиями, которые посылают точку $(x,y,z)$ к четным перестановкам $(\pm x,\pm y,\pm z)$ с четным количеством знаков минус. Преобразования $T_{i}$ составляют группу вращательных симметрий правильного тетраэдра .Преобразования $T_{i}M^{j}$ $(i=0,\ldots ,11$ , $j=0,\ldots ,4)$ составляют группу вращательных симметрий правильного икосаэдра .Тогда 60 баллов $T_{i}M^{j}p$ являются вершинами курносого додекадодекаэдра. Длина ребра равна $2(\xi +1){\sqrt {\xi ^{2}-\xi }}$ , радиус описанной окружности равен $(\xi +1){\sqrt {2\xi ^{2}-\xi }}$ , а средний радиус равен $\xi ^{2}+\xi$ .

Для большого курносого икосододекаэдра, длина ребра которого равна 1,радиус описанной окружности

R={\frac {1}{2}}{\sqrt {\frac {2\xi -1}{\xi -1}}}\approx 0.8516302281174128

Его средний радиус

r={\frac {1}{2}}{\sqrt {\frac {\xi }{\xi -1}}}\approx 0.6894012223976083

Другой вещественный корень P играет аналогичную роль в описании курносого додекадодекаэдра.

Связанные многогранники

Медиальный перевернутый пятиугольный шестиконтаэдр

Медиальный перевернутый пятиугольный шестиконтаэдр

Тип	Звездный многогранник
Лицо
Элементы	Ф = 60, Е = 150 V = 84 (χ = −6)
Группа симметрии	Я, [5,3] ⁺, 532
Ссылки на индексы	ВАМ ₆₀
двойной многогранник	Перевернутый курносый додекадодекаэдр

Медиальный перевернутый пятиугольный шестигранник (или среднелепестковый дитриаконтаэдр ) — невыпуклый равногранный многогранник . Это двойник однородного перевернутого курносого додекадодекаэдра. Его грани представляют собой неправильные невыпуклые пятиугольники с одним очень острым углом.

Пропорции

Обозначим золотое сечение через $\phi$ , и пусть $\xi \approx -0.236\,993\,843\,45$ быть наибольшим (наименее отрицательным) действительным нулем многочлена $P=8x^{4}-12x^{3}+5x+1$ . Тогда каждая грань имеет три равных угла $\arccos(\xi )\approx 103.709\,182\,219\,53^{\circ }$ , один из $\arccos(\phi ^{2}\xi +\phi )\approx 3.990\,130\,423\,41^{\circ }$ и один из $360^{\circ }-\arccos(\phi ^{-2}\xi -\phi ^{-1})\approx 224.882\,322\,917\,99^{\circ }$ . Каждая грань имеет одно ребро средней длины, два коротких и два длинных. Если средняя длина $2$ , то короткие ребра имеют длину $1-{\sqrt {\frac {1-\xi }{\phi ^{3}-\xi }}}\approx 0.474\,126\,460\,54,$ а длинные края имеют длину $1+{\sqrt {\frac {1-\xi }{\phi ^{-3}-\xi }}}\approx 37.551\,879\,448\,54.$ Двугранный угол равен $\arccos(\xi /(\xi +1))\approx 108.095\,719\,352\,34^{\circ }$ . Другой действительный ноль многочлена $P$ аналогичную роль играет средний пятиугольный гексеконтаэдр .