Треугольник Шварца

В геометрии треугольник Шварца , названный в честь Германа Шварца , представляет собой сферический треугольник , который можно использовать для мозаики сферы . ( сферическая мозаика ), возможно, перекрывающейся, посредством отражений в ее краях Они были классифицированы Шварцем (1873) .
В более общем смысле их можно определить как мозаику сферы, евклидовой плоскости или гиперболической плоскости . Каждый треугольник Шварца на сфере определяет конечную группу , а на евклидовой или гиперболической плоскости они определяют бесконечную группу.
Треугольник Шварца представлен тремя рациональными числами ( p q r ) , каждое из которых представляет угол в вершине. Значение n ⁄ d означает, что угол при вершине равен d ⁄ n полукруга. «2» означает прямоугольный треугольник . Когда это целые числа, треугольник называется треугольником Мёбиуса и соответствует непересекающейся мозаике, а группа симметрии называется группой треугольников . В сфере имеется три треугольника Мёбиуса плюс одно однопараметрическое семейство; на плоскости имеются три треугольника Мёбиуса, а в гиперболическом пространстве существует трёхпараметрическое семейство треугольников Мёбиуса и нет исключительных объектов .
Пространство решений
[ редактировать ]Фундаментальный треугольник домена ( pqr ) с углами при вершинах π ⁄ p , π ⁄ q и π ⁄ r , может существовать в разных пространствах в зависимости от значения суммы обратных чисел этих целых чисел:
Это просто способ сказать, что в евклидовом пространстве сумма внутренних углов треугольника равна π , тогда как на сфере они дают угол, больший, чем π , а в гиперболическом пространстве — меньший.
Графическое представление
[ редактировать ]Треугольник Шварца графически изображается треугольным графиком . Каждый узел представляет собой ребро (зеркало) треугольника Шварца. Каждое ребро помечается рациональным значением, соответствующим порядку отражения, т.е. π/ угол вершины .
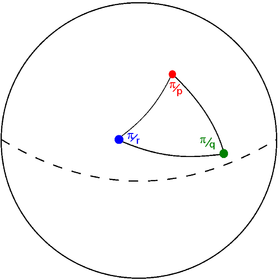 Черный треугольник ( p q r ) на сфере |  График треугольника Шварца |
Края второго порядка представляют собой перпендикулярные зеркала, которые на этой диаграмме можно игнорировать. Диаграмма Коксетера-Динкина представляет собой этот треугольный граф со скрытыми ребрами второго порядка.
Группу Кокстера можно использовать для более простых обозначений, например ( p q r ) для циклических графов и ( p q 2) = [ p , q ] для (прямоугольных треугольников) и ( p 2 2) = [ p ]× [].
Список треугольников Шварца
[ редактировать ]Треугольники Мёбиуса для сферы
[ редактировать ] (2 2 2) или [2,2] |  (3 2 2) или [3,2] | ... |
|---|---|---|
 (3 3 2) или [3,3] |  (4 3 2) или [4,3] |  (5 3 2) или [5,3] |
Треугольники Шварца с целыми числами, также называемые треугольниками Мёбиуса , включают одно 1-параметрическое семейство и три исключительных случая:
- [ p ,2] или ( p 2 2) – двугранная симметрия ,





- [3,3] или (3 3 2) – тетраэдрическая симметрия ,





- [4,3] или (4 3 2) – Октаэдрическая симметрия ,





- [5,3] или (5 3 2) – икосаэдрическая симметрия ,





Треугольники Шварца для сферы по плотности
[ редактировать ]Треугольники Шварца ( p q r ), сгруппированные по плотности :
| Плотность | двугранный | Тетраэдрический | Октаэдрический | икосаэдрический |
|---|---|---|---|---|
| д | ( 2 2 н / д ) | |||
| 1 | ( 2 3 3) | ( 2 3 4) | ( 2 3 5) | |
| 2 | (3/2 3 3) | (3/2 4 4) | (3/2 5 5), (5/2 3 3) | |
| 3 | ( 2 3/2 3) | ( 2 5/2 5) | ||
| 4 | (3 4/3 4) | (3 5/3 5) | ||
| 5 | ( 2 3/2 3/2) | ( 2 3/2 4) | ||
| 6 | (3/2 3/2 3/2) | (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) | ||
| 7 | ( 2 3 4/3) | ( 2 3 5/2) | ||
| 8 | (3/2 5/2 5) | |||
| 9 | ( 2 5/3 5) | |||
| 10 | (3 5/3 5/2), (3 5/4 5) | |||
| 11 | ( 2 3/2 4/3) | ( 2 3/2 5) | ||
| 13 | ( 2 3 5/3) | |||
| 14 | (3/2 4/3 4/3) | (3/2 5/2 5/2), (3 3 5/4) | ||
| 16 | (3 5/4 5/2) | |||
| 17 | ( 2 3/2 5/2) | |||
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) | |||
| 19 | ( 2 3 5/4) | |||
| 21 | ( 2 5/4 5/2) | |||
| 22 | (3/2 3/2 5/2) | |||
| 23 | ( 2 3/2 5/3) | |||
| 26 | (3/2 5/3 5/3) | |||
| 27 | ( 2 5/4 5/3) | |||
| 29 | ( 2 3/2 5/4) | |||
| 32 | (3/2 5/4 5/3) | |||
| 34 | (3/2 3/2 5/4) | |||
| 38 | (3/2 5/4 5/4) | |||
| 42 | (5/4 5/4 5/4) |
Треугольники для евклидовой плоскости
[ редактировать ] (3 3 3) |  (4 4 2) |  (6 3 2) |
Плотность 1:
- (3 3 3) – 60-60-60 ( равносторонние ),



- (4 4 2) – 45-45-90 (равнобедренная правая),





- (6 3 2) – 30-60-90 ,





Плотность 2:
- (6 6 3/2) — треугольник 120-30-30
Плотность ∞:
- (4 4/3 ∞)
- (3 3/2 ∞)
- (6 6/5 ∞)
Треугольники для гиперболической плоскости
[ редактировать ] (7 3 2) |  (8 3 2) |  (5 4 2) |
 (4 3 3) |  (4 4 3) |  (∞ ∞ ∞) |
| Основные области треугольников ( p q r ) | ||
Плотность 1:
- (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
- (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
- (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
- (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
- (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
- (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
- (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
- (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
- ...
- (∞ ∞ ∞)
Плотность 2:
- (3/2 7 7), (3/2 8 8), (3/2 9 9) ... (3/2 ∞ ∞)
- (5/2 4 4), (5/2 5 5), (5/2 6 6) ... (5/2 ∞ ∞)
- (7/2 3 3), (7/2 4 4), (7/2 5 5) ... (7/2 ∞ ∞)
- (9/2 3 3), (9/2 4 4), (9/2 5 5) ... (9/2 ∞ ∞)
- ...
Плотность 3:
- (2 7/2 7), (2 9/2 9), (2 11/2 11) ...
Плотность 4:
- (7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11) ...
Плотность 6:
- (7/4 7 7), (9/4 9 9), (11/4 11 11) ...
- (7/2 7/2 7/2), (9/2 9/2 9/2), ...
Плотность 10:
- (3 7/2 7)
Треугольник Шварца (2 3 7) является наименьшим гиперболическим треугольником Шварца и поэтому представляет особый интерес. Его группа треугольников (или, точнее, группа фон Дейка индекса 2 изометрий, сохраняющих ориентацию) — это (2,3,7) группа треугольников , которая является универсальной группой для всех групп Гурвица — максимальных групп изометрий римановых поверхностей . Все группы Гурвица являются факторами группы треугольников (2,3,7), а все поверхности Гурвица замощены треугольником Шварца (2,3,7). Наименьшая группа Гурвица — это простая группа порядка 168, вторая наименьшая неабелева простая группа , изоморфная PSL(2,7) , а соответствующая поверхность Гурвица (рода 3) — квартика Клейна .
Треугольник (2 3 8) замощает поверхность Больца , высокосимметричную (но не Гурвиц) поверхность рода 2.
Перечисленные выше треугольники с одним нецелым углом были впервые классифицированы Энтони В. Кнаппом . [1] Список треугольников с кратными нецелыми углами приведен в . [2]
Тесселяция треугольниками Шварца
[ редактировать ]В этом разделе с использованием элементарных методов будет обсуждаться замощение гиперболической верхней полуплоскости треугольниками Шварца. элементарный подход Каратеодори (1954) Для треугольников без «каспов» — углов, равных нулю или, что эквивалентно, вершин на действительной оси — будет использоваться . Для треугольников с одной или двумя точками возврата будут использоваться элементарные рассуждения Эванса (1973) , упрощающие подход Хекке (1935) : в случае треугольника Шварца с одним углом нулевым, а другим прямым углом, сохраняется ориентация Подгруппа группы отражения треугольника является группой Гекке . Для идеального треугольника, в котором все углы равны нулю, так что все вершины лежат на вещественной оси, существование мозаики будет установлено путем соотнесения ее с рядом Фейри, описанным в Hardy & Wright (2008) и Series (2015) . В этом случае мозаику можно рассматривать как мозаику, связанную с тремя соприкасающимися кругами на сфере Римана , предельный случай конфигураций, связанных с тремя непересекающимися невложенными кругами и их группами отражений, так называемую « Группы Шоттки », подробно описанные в Mumford, Series & Wright (2015) . Альтернативно — разделив идеальный треугольник на шесть треугольников с углами 0, π /2 и π /3 — мозаику идеальными треугольниками можно понять с точки зрения мозаика треугольниками с одной или двумя вершинами.
Треугольники без точек пересечения
[ редактировать ]


Предположим, что гиперболический треугольник Δ имеет углы π / a , π / b и π / c с целыми числами a , b , c больше 1. Гиперболическая площадь треугольника Δ равна π – π / a – π / b – π / c , так что
Построение мозаики сначала будет осуществляться для случая, когда a , b и c больше 2. [3]
Исходный треугольник Δ дает выпуклый многоугольник P 1 с 3 вершинами. В каждой из трех вершин треугольник можно последовательно отразить через ребра, исходящие из вершин, чтобы создать 2 млн копий треугольника, где угол в вершине равен π / m . Треугольники не перекрываются, за исключением краев, половина из них имеет обратную ориентацию и совмещается, образуя мозаику окрестностей точки. Объединение этих новых треугольников вместе с исходным треугольником образует связную фигуру P 2 . Он состоит из треугольников, которые пересекаются только по краям или вершинам, образует выпуклый многоугольник со всеми углами, меньшими или равными π , и каждая сторона является ребром отраженного треугольника. В случае, когда угол Δ равен π /3, вершина P 2 будет иметь внутренний угол π , но это не влияет на выпуклость P 2 . Даже в этом вырожденном случае, когда возникает угол π , два коллинеарных края по-прежнему считаются различными для целей построения.
Построение P 2 можно понять более ясно, заметив, что некоторые треугольники или плитки добавляются дважды, причем три из них имеют общую сторону с исходным треугольником. Остальные имеют только одну общую вершину. Более систематический способ укладки мозаики — сначала добавить по плитке к каждой стороне (отражение треугольника на этом ребре), а затем заполнить промежутки в каждой вершине. В результате всего получается 3 + (2 a – 3) + (2 b – 3) + (2 c – 3) = 2( a + b + c ) – 6 новых треугольников. Новые вершины бывают двух типов. Те, которые являются вершинами треугольников, прикрепленных к сторонам исходного треугольника, которые соединены с двумя вершинами Δ. Каждый из них лежит в трех новых треугольниках, пересекающихся в этой вершине. Остальные соединены с единственной вершиной треугольника Δ и принадлежат двум новым треугольникам, имеющим общее ребро. Таким образом, имеется 3 + (2 a – 4) + (2 b – 4) + (2 c – 4) = 2( a + b + c ) – 9 новых вершин. По конструкции перекрытия отсутствуют. Чтобы увидеть, что P 2 выпукла, достаточно увидеть, что угол между сторонами, сходящимися в новой вершине, составляет угол, меньший или равный π . Но новые вершины лежат в двух или трех новых треугольниках, которые пересекаются в этой вершине, поэтому угол в этой вершине не превышает 2 π /3 или π , как и требуется.
Этот процесс можно повторить для P2 , чтобы получить , сначала добавляя плитки к каждому краю P2 , а затем заполняя плитки вокруг каждой вершины P2 P3 . Затем процесс можно повторить от P 3 , чтобы получить P 4 и так далее, последовательно производя P n из P n – 1 . Индуктивно можно проверить, что все это выпуклые многоугольники с непересекающимися плитками.Действительно, как и на первом этапе процесса, при построении P n из P n – 1 существует два типа плиток : те, которые прикреплены к ребру P n – 1 , и те, которые прикреплены к одной вершине. Аналогично, существует два типа вершин: в одной встречаются две новые плитки, а в другой — три плитки. Таким образом, при условии, что плитки не перекрываются, предыдущий аргумент показывает, что углы при вершинах не превышают π и, следовательно, P n — выпуклый многоугольник. [а]
Поэтому необходимо убедиться, что при построении P n из P n − 1 : [4]
(a) новые треугольники не перекрываются с P n − 1, за исключением случаев, уже описанных;
(б) новые треугольники не перекрываются друг с другом, за исключением случаев, уже описанных;
(в) геодезическая из любой точки Δ до вершины многоугольника P n – 1 составляет угол ≤ 2 π /3 с каждым из ребер многоугольника в этой вершине.
Чтобы доказать (а), заметим, что по выпуклости многоугольник P n − 1 является пересечением выпуклых полупространств, определяемых полными дугами окружностей, определяющими его границу. Таким образом, в данной вершине P n − 1 находятся две такие дуги окружности, определяющие два сектора: один сектор содержит внутренность P n − 1 , другой содержит внутренности новых треугольников, добавленных вокруг данной вершины. Это можно визуализировать, используя преобразование Мёбиуса, чтобы сопоставить верхнюю полуплоскость с единичным диском, а вершину с началом координат; внутренняя часть многоугольника и каждый из новых треугольников лежат в разных секторах единичного круга. Таким образом, (а) доказано.
Прежде чем доказывать (c) и (b), можно применить преобразование Мёбиуса, чтобы сопоставить верхнюю полуплоскость с единичным кругом, а фиксированную точку внутри Δ — с началом координат.
Доказательство (в) проводится по индукции. Обратите внимание, что радиус, соединяющий начало координат с вершиной многоугольника P n − 1, образует угол меньше 2 π /3 с каждым из ребер многоугольника в этой вершине, если ровно два треугольника из P n − 1 пересекаются в вершине. вершине, поскольку каждый из них имеет угол, меньший или равный π /3 в этой вершине. Чтобы проверить, верно ли это, когда три треугольника P n − 1 встречаются в вершине, скажем, C , предположим, что основание среднего треугольника находится на стороне AB из P n − 2 . Радиусы OA и OB углы, меньшие или равные 2π / по индукции образуют с ребром AB 3 . В этом случае область в секторе между радиусами ОА и ОВ вне ребра AB является выпуклой как пересечение трех выпуклых областей. По индукции углы A и B больше или равны π /3. Таким образом, геодезические, ведущие к C из A и B, начинаются в этом регионе; по выпуклости треугольник ABC целиком лежит внутри области. Четырехугольник OACB имеет все углы меньше π (поскольку OAB — геодезический треугольник), поэтому он выпуклый. Следовательно, радиус OC угла треугольника ABC вблизи C. лежит внутри Таким образом, углы между OC и двумя краями P n – 1, встречающимися в точке C, меньше или равны π /3 + π /3 = 2 π /3, как утверждается.
Для доказательства (б) надо проверить, как пересекаются новые треугольники Pn в .
Сначала рассмотрим плитки, добавленные к краям P n – 1 . Приняв обозначения, аналогичные (c), пусть AB — основание плитки, а C — третья вершина. Тогда радиусы OA и OB углы, меньшие или равные 2 π образуют с ребром AB /3 , и рассуждения доказательства (c) применимы для доказательства того, что треугольник ABC лежит внутри сектора, определяемого радиусами OA и OB. . Это верно для каждого ребра P n – 1 . Поскольку внутренности секторов, определяемых отдельными ребрами, не пересекаются, новые треугольники этого типа пересекаются только так, как утверждается.
Далее рассмотрим дополнительные плитки, добавленные для каждой вершины P n – 1 . Если считать вершину A , то три — это два ребра AB 1 и AB 2 из P n – 1, пересекаются в A. которые Пусть C 1 и C 2 — дополнительные вершины плиток, добавленных к этим ребрам. Теперь дополнительные плитки, добавленные в A , лежат в секторе, определенном радиусами OB 1 и OB 2 . Многоугольник с вершинами C 2 O , C 1 , а затем вершинами дополнительных плиток имеет все внутренние углы меньше π и, следовательно, является выпуклым. Следовательно, он полностью содержится в секторе, определяемом радиусами OC 1 и OC 2 . Поскольку внутренности этих секторов не пересекаются, это подразумевает все утверждения о том, как пересекаются добавленные плитки.


Наконец, осталось доказать, что замощение, образованное объединением треугольников, покрывает всю верхнюю полуплоскость. Любая точка z, мозаикой, лежит в многоугольнике и Pn , следовательно, в многоугольнике Pn покрытая +1 . Следовательно, он лежит в копии исходного треугольника Δ, а также в копии P 2 , полностью содержащейся в P n +1 . Гиперболическое расстояние между ∆ и внешностью P2 меньше равно r > 0. Таким образом, гиперболическое расстояние между z и точками, не покрытыми мозаикой, не r . Поскольку это относится ко всем точкам замощения, множество, покрытое замощением, замкнуто. С другой стороны, замощение является открытым, поскольку оно совпадает с объединением внутренностей многоугольников P n . Благодаря связности тесселяция должна охватывать всю верхнюю полуплоскость.
Чтобы понять, как действовать в случае, когда угол Δ является прямым, обратите внимание, что неравенство
- .
подразумевает, что если один из углов прямой, скажем a = 2, то оба угла b и c больше 2 и один из них, скажем b , должен быть больше 3. В этом случае отражение треугольника через сторону AB дает равнобедренный гиперболический треугольник с углами π / c , π / c и 2 π / b . Если 2 π / b ≤ π /3, т.е. b больше 5, то все углы удвоенного треугольника меньше или равны π /3. В этом случае построение мозаики, приведенной выше, посредством увеличения выпуклых многоугольников слово в слово адаптируется к этому случаю, за исключением того, что вокруг вершины с углом 2 π / b требуется только b , а не 2 b, копии треугольника, чтобы замостить окрестность. вершины. Это возможно, поскольку удвоенный треугольник является равнобедренным. Тесселяция для удвоенного треугольника дает результат для исходного треугольника, если разрезать все большие треугольники пополам. [5]
Осталось рассмотреть случай, когда b равно 4 или 5. Если b = 4, то c ≥ 5: в этом случае, если c ≥ 6, то b и c можно поменять местами, и применим приведенный выше аргумент, оставив случай b = 4. и c = 5. Если b = 5, то c ≥ 4. Случай c ≥ 6 можно решить, поменяв местами b и c , так что единственным дополнительным случаем будет b = 5 и c = 5. Этот последний равнобедренный треугольник является удвоенная версия первого исключительного треугольника, поэтому только этот треугольник Δ 1 — с углами π /2, π /4 и π /5 и гиперболической площадью π необходимо рассматривать /20 (см. ниже). Каратеодори (1954) рассматривает этот случай с помощью общего метода, который работает для всех прямоугольных треугольников, у которых два других угла меньше или равны π /4. Предыдущий метод построения P 2 , P 3 , ... модифицируется добавлением дополнительного треугольника каждый раз, когда угол 3 π в вершине возникает /2. Те же рассуждения применимы для доказательства отсутствия перекрытия и того, что мозаика покрывает гиперболическую верхнюю полуплоскость. [5]
С другой стороны, данная конфигурация порождает группу арифметических треугольников. Впервые они были изучены Фрике и Кляйном (1897) . и породили обширную литературу. В 1977 году Такеучи получил полную классификацию групп арифметических треугольников (их конечное число) и определил, когда две из них соизмеримы. Конкретный пример связан с кривой Бринга , и арифметическая теория подразумевает, что группа треугольников для Δ 1 содержит группу треугольников для треугольника Δ 2 с углами π / 4, π / 4 и π / 5 в качестве ненормальной подгруппы индекса. 6. [6]
Удваивая треугольники Δ1 и Δ2 , это означает, что должна существовать связь между 6 треугольниками Δ3 с углами π /2, π /5 и π /5 и гиперболической площадью π /10 и треугольником Δ4 с углами π / 5, π /5 и π /10 и гиперболическая площадь 3 π /5. Трелфолл (1932) установил такое соотношение непосредственно, совершенно элементарными геометрическими средствами, без обращения к теории арифметики: действительно, как показано на пятом рисунке ниже, четырехугольник, полученный отражением через сторону треугольника типа Δ 4, можно разложить по формуле 12 треугольников типа Δ 3 . Мозаику треугольниками типа Δ 4 можно выполнить основным методом этого раздела; следовательно, это доказывает существование мозаики треугольниками типа ∆3 и ∆1 . [7]
- Мозаика треугольниками с углами π /2, π /5 и π /5.
- Тесселяция, полученная путем объединения двух треугольников
- Замощение пятиугольниками, образованными из 10 (2,5,5) треугольников.
- Приспособление к замощению треугольниками с углами π /5, π /10, π /10
- Укладка 2 (5,10,10) треугольников 12 (2,5,5) треугольниками
Треугольники с одной или двумя вершинами
[ редактировать ]В случае треугольника Шварца с одной или двумя точками возврата процесс замощения упрощается; но легче использовать другой метод, восходящий к Гекке, чтобы доказать, что они исчерпывают гиперболическую верхнюю полуплоскость.
В случае одного возврата и ненулевых углов π / a , π / b с целыми числами a , b больше единицы, мозаику можно представить в единичном круге с вершиной, имеющей угол π / a в начале координат. Укладка мозаики начинается с добавления 2–1 копий треугольника в начале координат путем последовательных отражений. В результате получается многоугольник P 1 с 2 точками возврата и между каждыми двумя вершинами 2 a, каждая из которых имеет угол π / b . Следовательно, многоугольник выпуклый. Для каждой неидеальной вершины P 1 уникальный треугольник с этой вершиной можно аналогично отразить вокруг этой вершины, добавив таким образом 2 b – 1 новых треугольников, 2 b – 1 новых идеальных точек и 2 b – 1 новых вершин с углом π. / а . Таким образом, полученный многоугольник P 2 состоит из 2 a (2 b – 1) точек возврата и такого же количества вершин, каждая из которых имеет угол π / a , поэтому является выпуклым. Процесс можно продолжить таким образом, чтобы получить выпуклые многоугольники P 3 , P 4 и так далее. Многоугольник P n будет иметь вершины с углами, чередующимися между 0 и π / a для четного n и между 0 и π / b для нечетного n . По конструкции треугольники перекрываются только по краям или вершинам, поэтому образуют мозаику. [8]
Случай, когда треугольник имеет две вершины и один ненулевой угол π / a, можно свести к случаю одной вершины, заметив, что тринале является двойником треугольника с одной вершиной и ненулевыми углами π / a и π. / b с b = 2. Затем разбиение продолжается, как и раньше. [9]
Чтобы доказать, что они дают мозаику, удобнее работать в верхней полуплоскости. Оба случая можно рассматривать одновременно, поскольку случай двух точек возврата получается удвоением треугольника с одной точкой возврата и ненулевыми углами π / a и π /2. Итак, рассмотрим геодезический треугольник в верхней полуплоскости с углами 0, π / a , π / b и целыми числами a , b, большими единицы. Внутренность такого треугольника можно представить как область X в верхней полуплоскости, лежащую вне единичного круга | г | ≤ 1 и между двумя прямыми, параллельными мнимой оси, проходящим через точки u и v на единичной окружности. Пусть Γ — группа треугольников, порожденная тремя отражениями на сторонах треугольника.
Чтобы доказать, что последовательные отражения треугольника покрывают верхнюю полуплоскость, достаточно показать, что для любого в верхней полуплоскости существует g в Γ такой, что g ( z ) лежит в X. z Это следует из аргумента Эванса (1973) , упрощенного из теории групп Гекке . Пусть λ = Re a и µ = Re b, так что, не ограничивая общности, λ < 0 ⩽ µ. Три отражения по сторонам определяются выражением
Таким образом, T = R 3 ∘ R 2 является сдвигом на µ − λ. Отсюда следует, что для любого z 1 в верхней полуплоскости существует элемент g 1 в подгруппе Γ 1 группы Γ, порожденный T такой, что w 1 = g 1 ( z 1 ) удовлетворяет условию λ ⩽ Re w 1 ⩽ µ, т.е. эта полоса является фундаментальной областью для группы сдвигов Γ 1 . Если | ш 1 | ≥ 1, то w 1 лежит в X , и результат доказан. В противном случае пусть z 2 = R 1 ( w 1 ) и находят g 2 Γ 1 такой, что w 2 = g 2 ( z 2 ) удовлетворяет условию λ ⩽ Re w 2 ⩽ µ. Если | ш 2 | ≥ 1, то результат доказан. Продолжая таким же образом, либо некоторое w n удовлетворяет | ш н | ≥ 1, и в этом случае результат доказан; или | ш н | < 1 для всех n . Теперь, поскольку g n + 1 лежит в Γ 1 и | ш н | < 1,
В частности
и
Таким образом, из неравенства выше точки ( w n ) лежат в компакте | г | ≤ 1, λ ≤ Re z ≤ µ и Im z ≥ Im w 1 . Отсюда следует, что | ш н | стремится к 1; в противном случае существовало бы r < 1 такое, что | ш м | ≤ r для бесконечного числа m , и тогда последнее уравнение выше будет означать, что Im w n стремится к бесконечности, противоречие.
Пусть w — предельная точка w n , так что | ш | = 1. Таким образом, w лежит на дуге единичной окружности между u и v . Если w ≠ u , v , то R 1 w n будет лежать в X при достаточно большом n , вопреки предположению. Следовательно, w = u или v . при n достаточно большом wn Следовательно , лежит близко к u или v и, следовательно, должно лежать в одном из отражений треугольника относительно вершины u или v , поскольку они заполняют окрестности u и v . существует элемент g в Γ такой, что ( wn ) Таким образом , лежит в X. g Поскольку по построению w n находится на Γ-орбите точки z 1 , то на этой орбите существует точка, лежащая в X , что и требовалось. [10]
Идеальные треугольники
[ редактировать ]Мозаика для идеального треугольника со всеми его вершинами на единичной окружности и всеми углами 0 может рассматриваться как частный случай мозаики для треугольника с одной вершиной и двумя теперь нулевыми углами π /3 и π /2. Действительно, идеальный треугольник состоит из шести копий треугольника с одной вершиной, полученного отражением меньшего треугольника вокруг вершины с углом π /3.


Однако каждый шаг мозаики однозначно определяется положением новых точек возврата на окружности или, что то же самое, на действительной оси; и эти моменты можно понять непосредственно с точки зрения серии Фари, следующей за Series (2015) , Hatcher (2013 , стр. 20–32) и Hardy & Wright (2008 , стр. 23–31). Все начинается с основного шага, который создает мозаику — отражение идеального треугольника на одной из его сторон. Отражение соответствует процессу инверсии в проективной геометрии и принятию проективно-гармонического сопряжения , которое можно определить через перекрестное отношение . Фактически, если p , q , r , s — разные точки в сфере Римана, то существует единственное комплексное преобразование Мёбиуса g, переводящее p , q и s в 0, ∞ и 1 соответственно. Перекрестное отношение ( p , q ; r , s ) определяется как g ( r ) и определяется по формуле
По определению он инвариантен относительно преобразований Мёбиуса. Если a , b лежат на вещественной оси, гармоническое сопряжение c относительно a и b определяется как уникальное действительное число d такое, что ( a , b ; c , d ) = −1. Так, например, если a = 1 и b = –1, сопряженное число r равно 1/ r . В общем, инвариантность Мёбиуса можно использовать для получения явной формулы для d через a , b и c . Действительно, переводя центр t = ( a + b )/2 круга с диаметром, имеющим конечные точки a и b, в 0, d – t является гармонически сопряженным c – t относительно a – t и b – t . Радиус круга равен ρ = ( b – a )/2, поэтому ( d – t )/ρ является гармоническим сопряжением ( c – t )/ρ относительно 1 и -1. Таким образом
так что
Теперь будет показано, что существует параметризация таких идеальных треугольников, заданная рациональными числами в сокращенной форме.
где a и c удовлетворяют «условию соседства» p 2 q 1 − q 2 p 1 = 1.
Средний член b называется суммой Фарея или медианой внешних членов и записывается
Формула отраженного треугольника дает
Аналогично отраженный треугольник во втором полукруге дает новую вершину b ⊕ c . Непосредственно проверяется, что a и b удовлетворяют условию соседства, как и b и c .
Теперь эту процедуру можно использовать для отслеживания треугольников, полученных последовательным отражением базового треугольника Δ с вершинами 0, 1 и ∞. Достаточно рассмотреть полосу с 0 ≤ Re z ≤ 1, поскольку та же картина воспроизводится в параллельных полосках применением отражений в линиях Re z = 0 и 1. Идеальный треугольник с вершинами 0, 1, ∞ отражает в полукруге с основанием [0,1] в треугольник с вершинами a = 0, b = 1/2, c = 1. Таким образом, a = 0/1 и c = 1/1 являются соседями и b = a ⊕ c . Полукруг разделен на два меньших полукруга с основаниями [ a , b ] и [ b , c ]. Каждый из этих интервалов разделяется на два интервала одним и тем же процессом, в результате чего получается 4 интервала. Продолжая таким же образом, мы получаем подразделения на 8, 16, 32 интервала и так далее. На n -м этапе имеется 2 н соседние интервалы с 2 н + 1 конечная точка. Приведенная выше конструкция показывает, что последовательные конечные точки удовлетворяют условию соседства, так что новые конечные точки, возникающие в результате отражения, задаются формулой суммы Фарея.
Чтобы доказать, что мозаика покрывает всю гиперболическую плоскость, достаточно показать, что каждое рациональное число в [0,1] в конечном итоге встречается в качестве конечной точки. Есть несколько способов увидеть это. Один из наиболее элементарных методов описан в Graham, Knuth & Patashnik (1994) при развитии — без использования цепных дробей — теории дерева Штерна-Броко , которая кодифицирует новые рациональные конечные точки, появляющиеся на n -м уровне. этап. Они дают прямое доказательство существования всякого рационального. Действительно, начиная с {0/1,1/1}, последовательные конечные точки вводятся на уровне n +1 путем добавления сумм Фарея или медиан ( p + r )/( q + s ) между всеми последовательными членами p / q , r / s на n -м уровне (как описано выше). Пусть x = a / b — рациональное число, лежащее между 0 и 1, причем a и b взаимно простые. Предположим, что на некотором уровне x зажат между последовательными членами p / q < x < r / s . Эти неравенства вынуждают aq – bp ≥ 1 и br – as ≥ 1 и, следовательно, поскольку rp – qs = 1 ,
Это накладывает верхнюю границу на сумму числителей и знаменателей. С другой стороны, медиана ( p + r )/( q + s ) может быть введена и либо равна x , и в этом случае рациональный x появляется на этом уровне; или медиата дает новый интервал, содержащий x со строго большей суммой числителя и знаменателя. Таким образом, процесс должен завершиться не более чем через a + b шагов, тем самым доказывая, что x появляется. [11]
Второй подход основан на модулярной группе G = SL(2, Z ). [12] Алгоритм Евклида предполагает, что эта группа порождается матрицами
Фактически, пусть H будет подгруппой G, порожденной S и T . Позволять
быть элементом SL(2, Z ). Таким образом, ad − cb = 1, так что a и c взаимно просты. Позволять
Применяя при необходимости S , можно считать, что | а | > | с |(равенство невозможно в силу взаимной простоты). Пишем a = mc + r с0 ≤ р ≤ | с |. Но тогда
Этот процесс можно продолжать до тех пор, пока одна из записей не станет равна 0, и в этом случае другая обязательно будет равна ±1. Применяя при необходимости степень S , отсюда следует, что v = h u для некоторого h из H . Следовательно
с целыми числами p , q . Очевидно, p = 1, так что h −1 г = Т д . Таким образом, g = h T д лежит в H, как и требовалось.
Чтобы доказать, что все рациональные числа в [0,1] встречаются, достаточно показать, что G переносит ∆ на треугольники в мозаике. Это следует из того, что сначала отметим, что S и T переносят ∆ в такой треугольник: действительно, как и преобразования Мёбиуса, S ( z ) = –1/ z и T ( z ) = z + 1, поэтому они дают отражения ∆ в двух из его стороны. Но тогда S и T сопрягают отражения в сторонах Δ с отражениями в сторонах S Δ и T Δ, лежащих в Γ. Таким образом, G нормализует Γ. Поскольку треугольники в мозаике - это в точности треугольники формы g ∆ с g в Γ, отсюда следует, что S и T и, следовательно, все элементы G переставляют треугольники в мозаике. Поскольку каждое рациональное число имеет форму g (0) для g в G , каждое рациональное число в [0,1] является вершиной треугольника в мозаике.
Группу отражений и мозаику для идеального треугольника также можно рассматривать как предельный случай группы Шоттки для трех непересекающихся невложенных кругов на сфере Римана. И снова эта группа порождается гиперболическими отражениями в трех кругах. В обоих случаях три окружности имеют общую окружность, которая пересекает их перпендикулярно. Используя преобразование Мёбиуса, можно предположить, что это единичная окружность или, что то же самое, действительная ось в верхней полуплоскости. [13]
Подход Сигела
[ редактировать ]подход Карла Людвига Зигеля В этом подразделе изложен к теореме мозаики для треугольников. Менее элементарный подход Зигеля не использует выпуклость, вместо этого полагаясь на теорию римановых поверхностей , накрывающих пространств и версию теоремы монодромии для накрытий. Он был обобщен для доказательства более общей теоремы Пуанкаре о многоугольниках. (Обратите внимание, что частный случай замощения правильными n -угольниками с внутренними углами 2 π / n является непосредственным следствием мозаики треугольниками Шварца с углами π / n , π / n и π /2.) [14] [15]
Пусть Γ — свободное произведение Z 2 ∗ Z 2 ∗ Z 2 . Если Δ = ABC — треугольник Шварца с углами π / a , π / b и π / c , где a , b , c ≥ 2, то существует естественное отображение Γ на группу, порожденное отражениями в сторонах Δ. . Элементы Γ описываются произведением трех генераторов, где никакие два соседних генератора не равны. В вершинах A , B и C произведение отражений от сторон, встречающихся в вершине, определяют повороты на углы 2 π / a , 2 π / b и 2 π / c ; Пусть g A , g B и g C — соответствующие произведения образующих Γ = Z 2 ∗ Z 2 ∗ Z 2 . Пусть Г0 — нормальная подгруппа индекса 2 группы Г, состоящая из элементов, являющихся произведением четного числа образующих; и пусть Γ 1 — нормальная подгруппа Γ, порожденная ( g A ) а , ( г Б ) б и ( г С ) с . Они действуют на D тривиально. Пусть Γ = Γ/Γ 1 и Γ 0 = Γ 0 /Γ 1 .
Дизъюнктное объединение копий Δ, индексированных элементами из Γ с отождествлениями ребер, имеет естественную структуру римановой поверхности Σ. Во внутренней точке треугольника находится очевидная диаграмма. В качестве точки внутренней части ребра диаграмма получается путем отражения треугольника через ребро. В вершине треугольника с внутренним углом π / n карта получается из 2 n копий треугольника, полученных путем его последовательного отражения вокруг этой вершины. Группа Γ действует посредством преобразований колоды Σ, при этом элементы из Γ 0 действуют как голоморфные отображения, а элементы, не входящие в Γ 0, действуют как антиголоморфные отображения.
Существует естественное отображение P точки Σ в гиперболическую плоскость. Внутренность треугольника с меткой g в Γ переносится на g (Δ), ребра переходят на ребра, а вершины на вершины. Также легко проверить, что окрестность внутренней точки ребра берется в окрестность изображения; и аналогично для вершин. Таким образом, P является локально гомеоморфизмом и поэтому переводит открытые множества в открытые множества. Таким образом, образ P (Σ), т. е. объединение трансляций g ( Δ ), является открытым подмножеством верхней полуплоскости. С другой стороны, это множество также закрыто. Действительно, если точка находится достаточно близко к Δ, она должна находиться в сдвиге Δ . Действительно, окрестность каждой вершины заполнена отражениями Δ , и если точка лежит вне этих трех окрестностей, но все еще близка к Δ, она должна лежать на трех отражениях Δ в ее сторонах. Таким образом, существует δ > 0 такое, что если z находится на расстоянии меньшем, чем δ, от Δ , то z лежит в Γ -переносе Δ . Поскольку гиперболическое расстояние Γ -инвариантно, отсюда следует, что если z находится на расстоянии меньшем, чем δ, от Γ( Δ ), на самом деле он лежит в Γ( Δ ), поэтому это объединение замкнуто. Из связности следует, что P (Σ) — вся верхняя полуплоскость.
С другой стороны, P — локальный гомеоморфизм, то есть накрывающее отображение. Поскольку верхняя полуплоскость односвязна, отсюда следует, что P одноединичный и, следовательно, сдвиги Δ замощают верхнюю полуплоскость. Это является следствием следующей версии теоремы о монодромии для покрытий римановых поверхностей: если Q — отображение покрытия между римановыми поверхностями 1 и 2 , то любой путь из 2 можно поднять до пути в 1 и любой два гомотопических пути с одинаковыми концами поднимаются до гомотопических путей с одинаковыми конечными точками; непосредственным следствием является то, что если 2 односвязно, то Q должен быть гомеоморфизмом. [16] Чтобы применить это, пусть Σ 1 = Σ, пусть Σ 2 — верхняя полуплоскость и пусть Q = P . По следствию теоремы монодромии P должно быть однозначно.
Отсюда также следует, что g (∆) = ∆ тогда и только тогда, когда g лежит в Γ 1 , так что гомоморфизм Γ 0 в группу Мёбиуса является точным.
Группы гиперболического отражения
[ редактировать ]Мозаику треугольников Шварца можно рассматривать как обобщение теории бесконечных групп Кокстера , следуя теории гиперболических групп отражений , алгебраически развитой Жаком Титсом. [17] и геометрически Эрнестом Винбергом . [18] В случае с Лобачевским или гиперболической плоскостью идеи берут начало в работах Анри Пуанкаре и Вальтера фон Дейка девятнадцатого века . Однако, как Джозеф Ленер отметил в «Математических обзорах» , строгие доказательства того, что отражения треугольника Шварца порождают мозаику, часто были неполными, одним из примеров является его собственная книга 1964 года «Разрывные группы и автоморфные функции» . [19] [20] Строгими доказательствами являются элементарная трактовка Каратеодори в его учебнике Funktiontheorie 1950 года , переведенном на английский язык в 1954 году, и отчет Сигела 1954 года, использующий принцип монодромии. Здесь будет обобщен подход с использованием групп Кокстера в общих рамках классификации групп гиперболического отражения. [21]
Пусть r, s, t — символы и пусть a , b , c ≥ 2 — целые числа, возможно, ∞ , причем
Определим Γ как группу с представлением, имеющим генераторы r, s, t, которые все являются инволюциями и удовлетворяют условиям Если одно из целых чисел бесконечно, то произведение имеет бесконечный порядок. Генераторы r, s, t называются простыми отражениями .
Набор [22] Пусть e r , es с , e t — базис трехмерного вещественного векторного пространства V симметричной билинейной формой Λ такой, что с тремя диагональными элементами, равными одному. Симметричная билинейная форма Λ невырождена с сигнатурой (2, 1) . Определять:
Теорема (геометрическое представление). Операторы , τ являются инволюциями на V ρ, σ с соответствующими собственными векторами e r , e s , e t с простым собственным значением −1. Произведения операторов имеют порядок, соответствующий приведенному выше представлению (поэтому στ имеет порядок и a т. д.). Операторы ρ, σ, τ индуцируют представление Γ на V , сохраняющее Λ .
Билинейная форма Λ базиса имеет матрицу
так же имеет определитель Если , скажем, c = 2 , то собственные значения матрицы равны Состояние немедленно заставляет так что Λ должен иметь сигнатуру (2, 1) . Итак, в общем случае a , b , c ≥ 3 . Очевидно, что случай, когда все равны 3, невозможен. Но тогда определитель матрицы отрицателен, а ее след положителен. В результате два собственных значения положительны, а одно отрицательно, т.е. Λ имеет сигнатуру (2, 1) . Очевидно , ρ, σ, τ являются инволюциями, сохраняющими Λ с заданными −1 собственными векторами.
Чтобы проверить порядок произведений типа στ , достаточно отметить, что:
- отражения σ и τ порождают конечную или бесконечную группу диэдра ;
- двумерная линейная оболочка U es e ; и t τ инвариантна относительно σ и с ограничением Λ положительно определенным
- W , ортогональное дополнение к U , отрицательно определено на Λ , а и τ действуют тривиально на W. σ
(1) понятно, поскольку если γ = στ порождает нормальную подгруппу с σγσ −1 = с −1 . Для (2) U инвариантен по определению, а матрица положительно определена, поскольку Поскольку Λ имеет сигнатуру (2, 1) , ненулевой вектор w в W должен удовлетворять Λ( w , w ) < 0 . По определению, σ имеет собственные значения 1 и –1 на U , поэтому w должно быть зафиксировано σ . Аналогично w должно быть зафиксировано τ , чтобы (3) было доказано. Наконец в (1)
так что, если a конечно, собственные значения στ равны -1, ς и ς −1 , где и если a бесконечно, собственные значения равны -1, X и X −1 , где Более того, простой индукционный аргумент показывает, что если затем [23]
и если х > 0, то
Пусть Γ a — подгруппа диэдра в Γ, порожденная s и t , с аналогичными определениями для Γ b и Γ c . Аналогично определите Γ r как циклическую подгруппу Γ, заданную 2-группой {1, r }, с аналогичными определениями для Γ s и Γ t . По свойствам геометрического представления все шесть этих групп точно действуют на V . В частности Γ a можно отождествить с группой, порожденной σ и τ ; как и выше, оно явно разлагается в прямую сумму двумерного неприводимого подпространства U и одномерного подпространства W с тривиальным действием. Таким образом, существует единственный вектор в W, удовлетворяющем σ ( w ) = w и τ ( w ) = w . Явно,
Замечание о представлениях групп диэдра. Хорошо известно, что для конечномерных вещественных пространств со скалярными произведениями две ортогональные инволюции S и T могут быть разложены как ортогональная прямая сумма двумерных или одномерных инвариантных пространств; например, это можно вывести из наблюдения Пола Халмоша и других, что положительный самосопряженный оператор ( S – T ) 2 коммутирует как с S, так и с T . Однако в приведенном выше случае, когда билинейная форма Λ больше не является положительно определенным скалярным произведением, другие специальные необходимо привести рассуждения.
Теорема (Титса). Геометрическое представление группы Кокстера точное.
Этот результат был впервые доказан Титсом в начале 1960-х годов и впервые опубликован в тексте Бурбаки (1968) с его многочисленными упражнениями. В тексте фундаментальная палата была введена индуктивным аргументом; Упражнение 8 в §4 главы V было расширено Винаем Деодхаром для разработки теории положительных и отрицательных корней и, таким образом, сокращения исходного аргумента Титса. [24]
Пусть X — выпуклый конус сумм κ e r + λ e s + µ e t с вещественными неотрицательными коэффициентами, не все из которых равны нулю. Для g в группе Γ определим ℓ( g ) , длина слова или length , чтобы быть минимальным количеством отражений от r, s, t, необходимых для записи g как упорядоченной композиции простых отражений. Определим положительный корень как вектор g e r , g e s или g e r , лежащий в X , с g в Γ . [б]
Обычно по определениям проверяют, что [25]
- если | ℓ( гк ) – ℓ( г ) | = 1 для простого отражения q и, если g ≠ 1 , всегда существует простое отражение q такое, что ℓ( g ) = ℓ( gq ) + 1 ;
- для g и h в Γ , ℓ( gh ) ≤ ℓ( g ) + ℓ( h ) .
Предложение. Если g находится в Γ и ℓ( gq ) = ℓ( g ) ± 1 для простого отражения q , то g e q лежит в ± X и , следовательно, является положительным или отрицательным корнем в зависимости от знака.
При замене g на gq необходимо учитывать только положительный знак. Утверждение будет доказано индукцией по ℓ( g ) = m , оно тривиально при m = 0 .Предположим, что ℓ( gs ) = ℓ( g ) + 1 . Если ℓ( g ) = m > 0 , без ограничения общности можно предположить, что минимальное выражение для g заканчивается на ...t . Поскольку s и t порождают группу диэдра Γ a , g можно записать как произведение g = hk , где k = ( st ) н или т ( ст ) н и h имеет минимальное выражение, которое заканчивается на ...r , но никогда на s или t . Это означает, что ℓ( hs ) = ℓ( h ) + 1 и ℓ( ht ) = ℓ( h ) + 1 . Поскольку ℓ( h ) < m , предположение индукции показывает, что оба h e s , h e t лежат в X . Поэтому достаточно показать, что k e s имеет вид λ e s + µ e t с λ , µ ≥ 0 , а не оба 0. Но это уже проверено в формулах выше. [25]
Следствие (доказательство теоремы Титса). Геометрическое представление верно.
Достаточно показать, что если фиксирует er , es то , e g t , g = 1 . Учитывая минимальное выражение для g ≠ 1 , условия ℓ( gq ) = ℓ( g ) + 1 явно не могут быть одновременно удовлетворены тремя простыми отражениями q .
Обратите внимание, что, как следствие теоремы Титса, генераторы (слева) удовлетворяют условиям (справа): Это дает представление о сохраняющей ориентацию нормальной подгруппе индекса 2 Γ 1 группы Γ . Представление соответствует фундаментальной области, полученной путем отражения двух сторон геодезического треугольника с образованием геодезического параллелограмма (частный случай теоремы Пуанкаре о многоугольнике). [26]
Дальнейшие последствия. Корни представляют собой непересекающееся объединение положительных и отрицательных корней. Простое отражение q переставляет каждый положительный корень, кроме e q . Для g в Γ благодаря ℓ( g ) — это количество положительных корней, ставших отрицательными g .
Фундаментальная область и конус Титса. [27]
Пусть G — трехмерная замкнутая подгруппа Ли группы GL( V ), сохраняющая Λ . Поскольку V можно отождествить с трехмерным пространством Лоренца или Минковского с сигнатурой (2,1) , группа G изоморфна группе Лоренца O(2,1) и, следовательно, [с] Выбирая e в качестве положительного корневого вектора в X , стабилизатор e представляет собой максимальную компактную подгруппу K группы G, изоморфную O(2) . Однородное пространство X = G / K — симметричное пространство постоянной отрицательной кривизны, которое можно отождествить с двумерным гиперболоидом или плоскостью Лобачевского. . Дискретная группа Γ действует разрывно на G / K : фактор-пространство Γ \ G / K компактно, если все a, b, c конечны, и имеют конечную площадь в противном случае. Результаты о фундаментальной камере Титса имеют естественную интерпретацию в терминах соответствующего треугольника Шварца, что непосредственно переводится в свойства мозаики геодезического треугольника через гиперболическую группу отражений Γ . Переход от групп Кокстера к мозаике впервые можно найти в упражнениях §4 главы V Бурбаки (1968) , принадлежащих Титсу, и у Ивахори (1966) ; в настоящее время доступно множество других эквивалентных методов лечения, не всегда непосредственно сформулированных в терминах симметричных пространств.
Подход Маскита, де Рама и Бердона
[ редактировать ]Маскит (1971) дал общее доказательство теоремы Пуанкаре о многоугольниках в гиперболическом пространстве; аналогичное доказательство было дано в работе де Рама (1971) . Специализируясь на гиперболической плоскости и треугольниках Шварца, это можно использовать для создания современного подхода к установлению существования мозаики треугольников Шварца, как описано в Бердоне (1983) и Маските (1988) . Швейцарские математики де ла Гарп (1991) и Хефлигер представили вводный отчет, взяв геометрическую теорию групп . за отправную точку [28]
См. также
[ редактировать ]- Список однородных многогранников по треугольнику Шварца
- Символ Витхоффа
- Строительство Витхоффа
- Однородный многогранник
- Невыпуклый однородный многогранник
- Плотность (многогранник)
- Тетраэдр Гурса
- Регулярная гиперболическая мозаика
- Равномерные мозаики в гиперболической плоскости
Примечания
[ редактировать ]Ссылки
[ редактировать ]- ^ AW Knapp, Дважды порожденные фуксовы группы , Michigan Mathematical Journal 15 (1968), вып. 3, 289–304
- ^ Клименко и Сакума, Дискретные подгруппы с двумя образующими в Isom(H 2 ), содержащие элементы, меняющие ориентацию , Geometriae Dedicata Октябрь 1998 г., том 72, выпуск 3, стр. 247–282.
- ^ Каратеодори 1954 , стр. 177–181.
- ↑ Каратеодори, 1954 , стр. 178–180.
- ^ Jump up to: Перейти обратно: а б Каратеодори, 1954 , стр. 181–182.
- ^ См.:
- ^ См.:
- Threlfall 1932 , стр. 20–22, рисунок 9.
- Вебер 2005 г.
- ^ Каратеодори 1954 , с. 183
- ^ Каратеодори 1954 , с. 184
- ^ См.:
- Эванс 1973 , стр. 108–109.
- Берндт и Кнопп, 2008 г. , стр. 16–17.
- ^ Грэм, Кнут и Паташник 1994 , стр. 118
- ^ Серия 2015 г.
- ^ См.:
- ^ Сигел 1971 , стр. 85–87.
- ^ Доказательства теоремы Пуанкаре о многоугольниках см.
- Маски 1971 г.
- де Рам 1971 г.
- Бердон 1983 , стр. 242–249.
- Иверсен 1992 , стр. 200–208.
- Эпштейн и Петронио 1994 г.
- Бергер 2010 , стр. 616–617.
- ^ Бердон 1984 , стр. 106–107, 110–111.
- ^ См.:
- ^ См.:
- ^ Ленер 1964
- ^ Маски 1971 г.
- ^ См.:
- ^ Хекман 2018 .
- ^ Хоулетт 1996
- ^ См.:
- ^ Jump up to: Перейти обратно: а б Видеть:
- ^ См.:
- ^ См.:
- ^ См.:
- Милнор 1975 г.
- Бердон 1983 , стр. 242–249.
- Иверсен 1992 , стр. 200–208.
- Бридсон и Хефлигер, 1999 г.
- Бергер 2010 , стр. 616–617.
- Коксетер, HSM (1973), Правильные многогранники (Третье изд.), Dover Publications, ISBN 0-486-61480-8 , Таблица 3: Треугольники Шварца
- Шварц, Х.А. (1873), «О тех случаях, когда гипергеометрический ряд Гаусса представляет собой алгебраическую функцию своего четвертого элемента» , Журнал чистой и прикладной математики , 1873 (75): 292–335, doi : 10.1515/crll.1873.75 .292 , ISSN 0075-4102 , S2CID 121698536 (Обратите внимание, что Коксетер ссылается на это как на «К теории гипергеометрического ряда», это краткое название, используемое в заголовках страниц журнала).
- Веннингер, Магнус Дж. (1979), «Введение в понятие многогранной плотности», Сферические модели , Архив CUP, стр. 132–134 , ISBN 978-0-521-22279-2
- Абраменко, Петр; Браун, Кеннет С. (2007). Здания: теория и приложения . Тексты для аспирантов по математике. Том. 248. Шпрингер-Верлаг . ISBN 978-0-387-78834-0 . МР 2439729 .
- Бердон, Алан Ф. (1983), «Теорема Пуанкаре», Геометрия дискретных групп , Тексты для аспирантов по математике, том. 91, Спрингер, стр. 242–252, ISBN. 0-387-90788-2
- Бердон, Алан Ф. (1984), «Букварь по римановым поверхностям» , Серия лекций Лондонского математического общества , 78 , Cambridge University Press, ISBN 0521271045
- Бергер, Марсель (2010), Раскрытая геометрия. Лестница Иакова к современной высшей геометрии , перевод Лестера Сенешала, Springer, ISBN 978-3-540-70996-1
- Берндт, Брюс С .; Кнопп, Марвин И. (2008), Теория модулярных форм Гекке и ряды Дирихле , Монографии по теории чисел, том. 5, Всемирный научный, ISBN 978-981-270-635-5
- Бурбаки, Николя (1968). «Глава IV: Группы Кокстера и системы Титса • Глава V: Группы, порожденные отражениями». Группы и алгебры Ли . Элементы математики (на французском языке). Париж: Германн. стр. 1–56, 57–141. МР 0240238 . Перепечатано Массоном в 1981 году как ISBN 2-225-76076-4 .
- Бридсон, Мартин Р .; Хефлигер, Андре (1999). «I. Основной материал по SL 2 (R), дискретным подгруппам и верхней полуплоскости». Метрические пространства неположительной кривизны (PDF) . Основные принципы математических наук. Том 319. Шпрингер-Верлаг . ISBN 3-540-64324-9 . МР 1744486 .
- Браун, Кеннет С. (1989). Здания . Спрингер-Верлаг . ISBN 0-387-96876-8 . МР 0969123 .
- Каратеодори, Константин (1954), Теория функций комплексной переменной , вып. 2, перевод Ф. Стейнхардта, Челси
- Дэвис, Майкл В. (2008), «Приложение D. Геометрическое представление», Геометрия и топология групп Кокстера , Монографии Лондонского математического общества, том. 32, Princeton University Press , стр. 439–447, ISBN. 978-0-691-13138-2
- де ла Арп, Пьер (1991). «Приглашение в группы Кокстера». Теория групп с геометрической точки зрения (Триест, 1990) . Всемирная научная . стр. 193–253. МР 1170367 .
- Деодхар, Винай В. (1982). «О корневой системе группы Кокстера». Комм. Алгебра . 10 (6): 611–630. дои : 10.1080/00927878208822738 . МР 0647210 .
- Деодхар, Винай В. (1986). «Некоторые характеристики групп Кокстера» . Энсен. Математика. 32 : 111–120. МР 0850554 .
- де Рам, Г. (1971). «О многоугольниках, порождающих фуксовы группы» . Учите. Математика. (на французском языке). 17 :49–61.
- Эллис, Грэм (2019). «Треугольные группы». Приглашение к вычислительной гомотопии . Издательство Оксфордского университета . стр. 441–444. ISBN 978-0-19-883298-0 . МР 3971587 .
- Эпштейн, Дэвид Б.А .; Петронио, Карло (1994). «Изложение теоремы Пуанкаре о многограннике» . Энсен. Математика. 40 : 113–170. МР 1279064 .
- Эванс, Рональд (1973), «Фундаментальная область модульной группы Хекке», Journal of Number Theory , 5 (2): 108–115, Бибкод : 1973JNT.....5..108E , doi : 10.1016/0022- 314x(73)90063-2
- Фрике, Роберт ; Кляйн, Феликс (1897), Лекции по теории автоморфных функций. Первый том; Основы теории групп (на немецком языке), Б. Г. Тойбнер, ISBN 978-1-4297-0551-6 , ЯФМ 28.0334.01
- Грэм, Рональд Л .; Кнут, Дональд Э .; Паташник, Орен (1994), Конкретная математика (2-е изд.), Аддисон-Уэсли, стр. 116–118, ISBN 0-201-55802-5
- Харди, штат Джорджия ; Райт, Э.М. (2008), Введение в теорию чисел (6-е изд.), Oxford University Press, ISBN 978-0-19-921986-5
- Хэтчер, Аллен (2013). «1. Диаграмма Фарея». Топология чисел (PDF) . Корнеллский университет . Проверено 25 февраля 2022 г.
- Хекке, Э. (1935), «Об определении рядов Дирихле их функциональным уравнением», Mathematical Annals (на немецком языке), 112 : 664–699, doi : 10.1007/bf01565437
- Хекман, Герт Дж. (2018). «Группы Кокстера» (PDF) . Университет Радбауд в Неймегене . Проверено 3 марта 2022 г.
- Хиллер, Ховард (1982). Геометрия групп Кокстера . Исследования по математике. Том. 54. Питман. ISBN 0-273-08517-4 . МР 0649068 .
- Хоулетт, Роберт (1996). «Введение в группы Кокстера» . Семинар по теории геометрических групп Австралийского национального университета . Сидней .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - Хамфрис, Джеймс Э. (1990). Группы отражения и группы Кокстера . Кембриджские исследования по высшей математике. Том. 29. Издательство Кембриджского университета . ISBN 0-521-37510-Х . МР 1066460 .
- Иверсен, Биргер (1992), Гиперболическая геометрия , Студенческие тексты Лондонского математического общества, том. 25, Издательство Кембриджского университета, ISBN 0-521-43508-0
- Ивахори, Нагаёси (1966). «О дискретных группах отражений на симметричных римановых многообразиях». Учеб. Американо-японский семинар по дифференциальной геометрии (Киото, 1965 г.) . Токио: Ниппон Хёронша. стр. 57–62. МР 0217741 .
- Ленер, Джозеф (1964), Разрывные группы и автоморфные функции , Математические обзоры, том. 8, Провиденс, Род-Айленд: Американское математическое общество, MR 0164033
- Магнус, Вильгельм (1974), Неевклидовы мозаики и их группы , Чистая и прикладная математика, том. 61, Академик Пресс
- Магнус, Вильгельм ; Каррасс, Авраам; Солитар, Дональд (1976). Комбинаторная теория групп: представления групп через генераторы и отношения (второе исправленное изд.). Дуврские книги . МР 0207802 .
- Маскит, Бернар (1971), «О теореме Пуанкаре для фундаментальных многоугольников», Успехи в математике , 7 (3): 219–230, doi : 10.1016/s0001-8708(71)80003-8
- Маскит, Бернард (1988). «Теорема Пуанкаре». Клейновы группы . Основные принципы математических наук. Том 287. Шпрингер-Верлаг . ISBN 3-540-17746-9 . МР 0959135 .
- Максвелл, Джордж (1982). «Сферические упаковки и гиперболические группы отражений» . Дж. Алгебра . 79 : 78–97. дои : 10.1016/0021-8693(82)90318-0 . МР 0679972 .
- МакМаллен, Кертис Т. (1998), «Хаусдорфова размерность и конформная динамика. III. Вычисление размерности», American Journal of Mathematics , 120 : 691–721, doi : 10.1353/ajm.1998.0031 , S2CID 15928775
- Милнор, Джон (1975). «О трехмерных многообразиях Брискорна M(p,q,r)». Узлы, группы и трехмерные многообразия (Статьи, посвященные памяти Р. Х. Фокса) . Энн. математики. Исследования. Том. 84. Издательство Принстонского университета . стр. 175–225. МР 0418127 .
- Мамфорд, Дэвид ; Сериал, Кэролайн ; Райт, Дэвид (2015), Жемчуг Индры. Видение Феликса Кляйна , издательство Кембриджского университета, ISBN 978-1-107-56474-9
- Серия, Кэролайн (2015), Цепные дроби и гиперболическая геометрия, Летняя школа LMS Лафборо (PDF) , получено 15 февраля 2017 г.
- Сигел, CL (1971), Темы теории комплексных функций , вып. II. Автоморфные функции и абелевы интегралы в переводе А. Шеницера; М. Треткофф, Wiley-Interscience, стр. 85–87, ISBN. 0-471-60843-2
- Стейнберг, Роберт (1968). Эндоморфизмы линейных алгебраических групп . Мемуары Американского математического общества . Том. 80. Американское математическое общество . МР 0230728 .
- Такеучи, Кисао (1977a), «Группы арифметических треугольников», Журнал Математического общества Японии , 29 : 91–106, doi : 10.2969/jmsj/02910091
- Такеучи, Кисао (1977b), «Классы соизмеримости групп арифметических треугольников», Журнал факультета естественных наук Токийского университета, раздел IA, Математика , 24 : 201–212.
- Трелфолл, В. (1932), «Групповые картинки» (PDF) , Трактаты математическо-физического класса Саксонской академии наук , 41 , Хирцель: 1–59
- Титс, Жак (2013). «Группы и геометрии Кокстера». У Ф. Букенхаута; Б.М. Мюльхерр; ДжП. Тиньоль ; Х. Ван Мальдегем (ред.). Œuvres/Собрание сочинений, Том I. Наследие европейской математики (на французском языке). Цюрих: Европейское математическое общество . стр. 803–817. ISBN 978-3-03719-126-2 . Эта рукопись стала основополагающим текстом теории групп Кокстера, использованным для подготовки главы IV книги Бурбаки «Группы и алгебры лжи» ; Впервые он был опубликован в 2001 году.
- Винберг, Эрнест Б. (1971). «Дискретные линейные группы, порожденные отражениями». Математика СССР-Известия . 5 (5). Перевод П. Флора: 1083–1119. Бибкод : 1971ИзМат...5.1083В . дои : 10.1070/IM1971v005n05ABEH001203 . МР 0302779 .
- Винберг, Эрнест Б. (1985). «Гиперболические группы отражений» . Российские математические обзоры . 40 (1). Перевод Дж. Вигольда. Лондонское математическое общество : 31–75. Бибкод : 1985РуМаС..40...31В . doi : 10.1070/RM1985v040n01ABEH003527 . S2CID 250912767 .
- Винберг, Эрнест Б .; Шварцман О.В. (1993). «Дискретные группы движений пространств постоянной кривизны». Геометрия II: Пространства постоянной кривизны . Энциклопедия математики. наук. Том. 29. Шпрингер-Верлаг . стр. 139–248. ISBN 3-540-52000-7 . МР 1254933 .
- Вебер, Маттиас (2005), «Маленький звездчатый додекаэдр Кеплера как риманова поверхность» , Pacific Journal of Mathematics , 220 : 167–182, doi : 10.2140/pjm.2005.220.167
![{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}\quad {\begin{cases}>1&\implies {\text {Sphere}}\\[2pt]=1&\implies {\text{Евклидова плоскость}}\\[2pt]<1&\implies {\text{Гиперболическая плоскость}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c781765fbaeffe4ee3f94e7b3cb51a404d10b98c)




























^{b}&=1,\\[2pt](rs)^{c}&= 1.\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd7ecf1d5c46800fc04eba2cea7eddf4e18209cf)
![{\displaystyle {\begin{aligned}A&={\begin{cases}\cos {\frac {\pi }{a}} & {\text{if }}a\geq 2{\text{конечно,} }\\[2pt]\cosh x,\ x>0&{\text{иначе.}}\end{cases}}\\[8pt]B&={\begin{cases}\cos {\frac {\pi } {b}}&{\text{if }}b\geq 2{\text{ конечно,}}\\[2pt]\cosh y,\ y>0&{\text{иначе.}}\end{cases }}\\[8pt]C&={\begin{cases}\cos {\frac {\pi }{c}}&{\text{if }}c\geq 2{\text{ конечно,}}\ \[2pt]\cosh z,\ z>0&{\text{иначе.}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3bc2020b035d2c11a118c23f7a15f0e8349a140)
![{\displaystyle {\begin{aligned}\Lambda (\mathbf {e} _{s},\mathbf {e} _{t})&=-A,\\[2pt]\Lambda (\mathbf {e} _{t},\mathbf {e} _{r})&=-B,\\[2pt]\Lambda (\mathbf {e} _{r},\mathbf {e} _{s})&= -C,\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bacd3a78ece3fb65695a97959deb4d2acd7b0cf1)
![{\displaystyle {\begin{aligned}\rho (\mathbf {v})&=\mathbf {v} -2\Lambda (\mathbf {v},\mathbf {e} _{r})\mathbf {e } _{r}\\[2pt]\sigma (\mathbf {v})&=\mathbf {v} -2\Lambda (\mathbf {v} ,\mathbf {e} _{s})\mathbf { e} _{s}\\[2pt]\tau (\mathbf {v})&=\mathbf {v} -2\Lambda (\mathbf {v} ,\mathbf {e} _{t})\mathbf {e} _{t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c908e760f5f2f0a01371ee2e77d3ee9f4e01a67c)






![{\displaystyle {\begin{aligned}{5}\sigma (\mathbf {e} _{s})&=- {\mathbf {e} }_{s},&\quad \tau (\mathbf {e } _{s})&=2\cos({\tfrac {\pi }{a}})\,\mathbf {e} _{s}+\mathbf {e} _{t},\\[2pt ]\sigma (\mathbf {e} _{t})&=2\cos({\tfrac {\pi }{a}})\,\mathbf {e} _{s}+\mathbf {e} _ {t},&\quad \tau (\mathbf {e} _{t})&=- {\mathbf {e} }_{t},\end{alignment}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee50c0dc8d5bc2decdf0f2453f821dabb7533a6)



![{\displaystyle {\begin{aligned}(\sigma \tau )^{m}({\mathbf {e} }_{s}) &=\left[{\frac {\sin(2m+1)\theta }{\sin \theta }}\right]{\mathbf {e} }_{s}+\left[{\frac {\sin 2m\theta }{\sin \theta }}\right]{\mathbf { e} }_{t},\\[4pt]\tau (\sigma \tau )^{m}({\mathbf {e} }_{s})&=\left[{\frac {\sin( 2m+1)\theta }{\sin \theta }}\right]{\mathbf {e} }_{s}+\left[{\frac {\sin(2m+2)\theta }{\sin \ тета }}\right]{\mathbf {e} }_{t},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b48fd6d6b2bf7d056c4874931112b041f2d1ac6)
![{\displaystyle {\begin{aligned}(\sigma \tau )^{m}({\mathbf {e} }_{s}) &=\left[{\frac {\sinh(2m+1)x} {\sinh x}}\right]{\mathbf {e} }_{s}+\left[{\frac {\sinh 2mx}{\sinh x}}\right]{\mathbf {e} }_{ t},\\[4pt]\lim _{x\to 0}\ (\sigma \tau )^{m}(\mathbf {e} _{s})&=(2m+1)\mathbf {e } _{s}+2m\mathbf {e} _{t};\\[12pt]\tau (\sigma \tau )^{m}({\mathbf {e} }_{s})&=\ left[{\frac {\sinh(2m+1)x}{\sinh x}}\right]{\mathbf {e} }_{s}+\left[{\frac {\sinh(2m+2) x}{\sinh x}}\right]{\mathbf {e} }_{t},\\[4pt]\lim _{x\to 0}\,\tau (\sigma \tau )^{m }(\mathbf {e} _{s})&=(2m+1)\mathbf {e} _{s}+(2m+2)\mathbf {e} _{t}.\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8afd090c1a27ca10876bb1fae31c6782be8375b4)


\ \ {\text{ st }}&h^{b}=1,\\[4pt](k&=rs)\ \ {\text{ st }}&k^{c}=1,\\[4pt]&&ghk=1.\end{ выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38956fd2255e8ebfbd33932b71059ae07f4df98b)



