Теорема о монодромии

Иллюстрация аналитического продолжения вдоль кривой (только конечное число дисков $U_{t}$ показаны).

Аналитическое продолжение по кривой натурального логарифма (показана только мнимая часть логарифма).

В комплексном анализе является теорема монодромии важным результатом об аналитическом продолжении комплексно -аналитической функции на большее множество. Идея состоит в том, что можно продолжить комплексно-аналитическую функцию (далее называемую просто аналитической функцией ) вдоль кривых, начинающихся в исходной области определения функции и заканчивающихся в большем множестве. Потенциальная проблема этого аналитического продолжения вдоль стратегии кривой заключается в том, что обычно существует множество кривых, которые заканчиваются в одной и той же точке в большем наборе. Теорема о монодромии дает достаточные условия для аналитического продолжения, чтобы давать одно и то же значение в данной точке независимо от кривой, используемой для достижения этой точки, так что результирующая расширенная аналитическая функция является четко определенной и однозначной.

Прежде чем сформулировать эту теорему, необходимо определить аналитическое продолжение вдоль кривой и изучить его свойства.

Аналитическое продолжение вдоль кривой

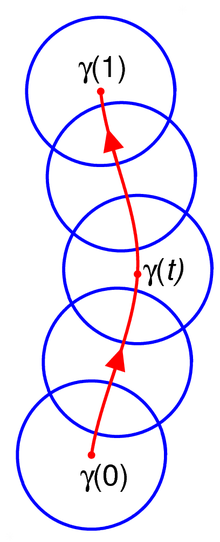
Определение аналитического продолжения вдоль кривой немного техническое, но основная идея состоит в том, что мы начинаем с аналитической функции, определенной вокруг точки, и расширяем эту функцию вдоль кривой с помощью аналитических функций, определенных на небольших перекрывающихся дисках, покрывающих эту кривую.

Формально рассмотрим кривую ( непрерывную функцию ) $\gamma :[0,1]\to \mathbb {C} .$ Позволять $f$ быть аналитической функцией, определенной на открытом диске $U$ сосредоточено в $\gamma (0).$ Аналитическое продолжение пары $(f,U)$ вдоль $\gamma$ это набор пар $(f_{t},U_{t})$ для $0\leq t\leq 1$ такой, что

• $f_{0}=f$ и $U_{0}=U.$

• Для каждого $t\in [0,1],U_{t}$ представляет собой открытый диск с центром в $\gamma (t)$ и $f_{t}:U_{t}\to \mathbb {C}$ является аналитической функцией.

• Для каждого $t\in [0,1]$ существует $\varepsilon >0$ такой, что для всех $t'\in [0,1]$ с $|t-t'|<\varepsilon$ у одного есть это $\gamma (t')\in U_{t}$ (что подразумевает, что $U_{t}$ и $U_{t'}$ имеют непустое пересечение ) и функции $f_{t}$ и $f_{t'}$ совпадают на пересечении $U_{t}\cap U_{t'}.$

Свойства аналитического продолжения вдоль кривой

Аналитическое продолжение вдоль кривой существенно однозначно в том смысле, что для данных двух аналитических продолжений $(f_{t},U_{t})$ и $(g_{t},V_{t})$ $(0\leq t\leq 1)$ из $(f,U)$ вдоль $\gamma ,$ функции $f_{1}$ и $g_{1}$ совпадать $U_{1}\cap V_{1}.$ Неформально это говорит о том, что любые два аналитических продолжения $(f,U)$ вдоль $\gamma$ в конечном итоге будут иметь те же значения в окрестности $\gamma (1).$

Если кривая $\gamma$ закрыто (т. $\gamma (0)=\gamma (1)$), не обязательно иметь $f_{0}$ равный $f_{1}$ в районе $\gamma (0).$ Например, если начать с точки $(a,0)$ с $a>0$ и комплексный логарифм, определенный в окрестности этой точки, и можно $\gamma$ быть кругом радиуса $a$ с центром в начале координат (движение против часовой стрелки от $(a,0)$), то, выполняя аналитическое продолжение вдоль этой кривой, получим значение логарифма при $(a,0)$ который $2\pi i$ плюс исходное значение (см. вторую иллюстрацию справа).

Теорема

Гомотопия с фиксированными эндоточками необходима для справедливости теоремы монодромии.

Как отмечалось ранее, два аналитических продолжения вдоль одной и той же кривой дают один и тот же результат в конечной точке кривой. Однако, учитывая две разные кривые, ответвляющиеся из одной и той же точки, вокруг которой определена аналитическая функция, с повторным соединением кривых на концах, в общем случае неверно, что аналитическое продолжение этой функции вдоль двух кривых будет давать одно и то же значение. в их общей конечной точке.

Действительно, можно рассматривать, как и в предыдущем разделе, комплексный логарифм, определенный в окрестности точки $(a,0)$ и круг с центром в начале координат и радиусом $a.$ Тогда можно путешествовать из $(a,0)$ к $(-a,0)$ двумя способами: против часовой стрелки - по дуге верхней полуплоскости этого круга и по часовой стрелке - по дуге нижней полуплоскости. Значения логарифма при $(-a,0)$ полученные аналитическим продолжением по этим двум дугам, будут отличаться на $2\pi i.$

Если же можно непрерывно деформировать одну из кривых в другую, сохраняя фиксированными начальную и конечную точки, и аналитическое продолжение возможно на каждой из промежуточных кривых, то аналитические продолжения вдоль двух кривых дадут одни и те же результаты при их общая конечная точка. Это называется теоремой монодромии , и ее формулировка уточняется ниже.

Позволять $U$ быть открытым диском в комплексной плоскости с центром в точке $P$ и $f:U\to \mathbb {C}$ быть комплексно-аналитической функцией. Позволять $Q$ быть еще одной точкой на комплексной плоскости. Если существует семейство кривых $\gamma _{s}:[0,1]\to \mathbb {C}$ с $s\in [0,1]$ такой, что $\gamma _{s}(0)=P$ и $\gamma _{s}(1)=Q$ для всех $s\in [0,1],$ функция $(s,t)\in [0,1]\times [0,1]\to \gamma _{s}(t)\in \mathbb {C}$ является непрерывным, и для каждого $s\in [0,1]$ можно сделать аналитическое продолжение $f$ вдоль $\gamma _{s},$ то аналитические продолжения $f$ вдоль $\gamma _{0}$ и $\gamma _{1}$ даст те же значения при $Q.$

Теорема монодромии позволяет расширить аналитическую функцию на больший набор с помощью кривых, соединяющих точку в исходной области определения функции с точками в большем наборе. Теорема ниже, которая утверждает это, также называется теоремой монодромии.

Позволять $U$ быть открытым диском в комплексной плоскости с центром в точке $P$ и $f:U\to \mathbb {C}$ быть комплексно-аналитической функцией. Если $W$ — открытое односвязное множество, содержащее $U,$ и можно провести аналитическое продолжение $f$ на любой кривой, содержащейся в $W$ который начинается в $P,$ затем $f$ допускает прямое аналитическое продолжение $W,$ это означает, что существует комплексно-аналитическая функция $g:W\to \mathbb {C}$ чьи ограничения на $U$ является $f.$

См. также

• Аналитическое продолжение
• Монодромия

Ссылки

• Кранц, Стивен Г. (1999). Справочник комплексных переменных . Биркхойзер. ISBN  0-8176-4011-8 .
• Джонс, Гарет А.; Сингерман, Дэвид (1987). Комплексные функции: алгебраическая и геометрическая точка зрения . Издательство Кембриджского университета. ISBN  0-521-31366-Х .

• Трибель, Ганс (1986). Анализ и математическая физика, англ. изд . Паб Д. Рейдель. компания ISBN  90-277-2077-0 .

Внешние ссылки

• Теорема монодромии в MathWorld
• Теорема монодромии в PlanetMath .
• Теорема монодромии в Математической энциклопедии