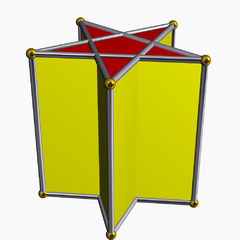
Пентаграммная призма
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
| Равномерная пентаграммная призма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | Ф = 7, Е = 15 V = 10 (χ = 2) |
| Лица по сторонам | 5{4}+2{ 5 / 2 } |
| Символ Шлефли | т{2, 5 / 2 } или { 5 / 2 }×{} |
| Символ Витхоффа | 2 5 / 2 | 2 |
| Диаграмма Кокстера | |
| Симметрия | D 5h , [5,2], (*522), порядок 20 |
| Группа вращения | Д 5 , [5,2] + , (522), порядок 10 |
| Ссылки на индексы | На 78(а) |
| Двойной | Пентаграммная дипирамида |
| Характеристики | невыпуклый |
 Вершинная фигура 4.4. 5 / 2 | |
В геометрии пентаграммная призма — одна из бесконечного множества невыпуклых призм, образованных квадратными сторонами и двумя правильными звездчатыми многоугольными вершинами, в данном случае двумя пентаграммами .
Это частный случай прямой призмы с пентаграммой в основании, которая обычно имеет прямоугольные грани без основания. Топологически это то же самое, что выпуклая пятиугольная призма .
Это 78-я модель в списке однородных многогранников , как первый представитель однородных звездных призм , наряду с пентаграммной антипризмой , которая является 79-й моделью.
Геометрия
[ редактировать ]У него 7 граней, 15 ребер и 10 вершин. Этот многогранник идентифицируется индексным названием U 78 как однородный многогранник . [1]
Треугольная грань имеет неоднозначную внутреннюю часть, поскольку она самопересекающаяся. Центральную область пятиугольника можно считать углом или внешней стороной, в зависимости от того, как определяется внутренняя часть. Одно из определений внутренней части — это набор точек, луч которых пересекает границу нечетное число раз, чтобы выйти за пределы диаметра.
Галерея
[ редактировать ] Альтернативное изображение пентаграмм с полыми центрами. |  3D-модель (равномерной) пентаграммной призмы |
Пентаграммная дипирамида
[ редактировать ]| Пентаграммная дипирамида | |
|---|---|
 | |
| Тип | Звездная бипирамида |
| Лица | 10 треугольников |
| Края | 15 |
| Вершины | 7 |
| Символ Шлефли | {} + {5/2} |
| Диаграмма Кокстера | |
| Группа симметрии | D 5h , [5,2], (*225), порядок 20 |
| Группа вращения | Д 5 , [5,2] + , (225), порядок 10 |
| Двойной многогранник | пентаграммная призма |
| Конфигурация лица | Версия 4.4.5 |
| Характеристики | грань-транзитивная , ( дельтаэдр ) |
В геометрии пентаграммная звездных дипирамид , дипирамида (или бипирамида ) является первой из бесконечного множества транзитивных по граням содержащих звездообразное многоугольное расположение ребер. Он имеет 10 пересекающихся граней равнобедренного треугольника . Топологически она идентична пятиугольной дипирамиде .
Каждая звездная дипирамида представляет собой двойную на основе звездного многоугольника однородную призму .
 3D-модель двойной однородной пентаграммной дипирамиды. |  3D модель пентаграммной дипирамиды с правильными гранями |
Связанные многогранники
[ редактировать ]Существует два пентаграммных трапецоэдра (или дельтоэдра), двойственных пентаграммной антипризме и пентаграммной скрещенной антипризме соответственно, каждая из которых имеет пересекающиеся грани в форме воздушного змея (выпуклые или вогнутые), и всего 12 вершин:
| { 5 ⁄ 2 } трапецоэдр | { 5 ⁄ 3 } трапецоэдра |
|---|---|
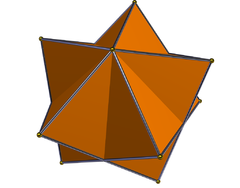 |  |
Ссылки
[ редактировать ]- ^ Медер, Роман. «78: пентаграммная призма» . МатКонсалт .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Пентаграммная призма» . Математический мир .
- Вайсштейн, Эрик В. «Пентаграммная дипирамида» . Математический мир .
- Вайсштейн, Эрик В. «Пентаграммный дельтоэдр» . Математический мир .
- Вайсштейн, Эрик В. «Пентаграмматический вогнутый дельтоэдр» . Математический мир .
- http://www.mathconsult.ch/showroom/unipoly/78.html
- http://bulatov.org/polyhedra/uniform/u03.html
- Бумажная модель пентаграммной призмы
- https://web.archive.org/web/20050313234702/http://www.math.technion.ac.il/~rl/kaleido/data/03.html
- https://web.archive.org/web/20060211140715/http://www.ac-noumea.nc/maths/amc/polyhedr/no_conv5_.htm
- Бумажная модель (сетка) Пентаграммная призма