Малый сложный икосододекаэдр

Малый сложный икосододекаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф =32, Е =60 (30х2) V = 12 (χ = −16)
Лица по сторонам	20{3}+12{5}
Диаграмма Кокстера
Символ Витхоффа	5 | 3/2 5
Группа симметрии	I h , [5,3], *532
Ссылки на индексы	У - , С - , Ш -
Двойной многогранник	Небольшой комплекс икозидодекакрон
Вершинная фигура	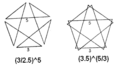(3/2.5) 5 (3.5) 5 /3
Аббревиатура Бауэрса	Сид

В геометрии малый комплексный икосододекаэдр представляет собой вырожденный однородный звездчатый многогранник . Его края удваиваются, что приводит к вырождению. У звезды 32 грани (20 треугольников и 12 пятиугольников ), 60 (сдвоенных) ребер, 12 вершин и 4 общие грани. Грани в нем рассматриваются как два перекрывающихся ребра топологического многогранника.

Небольшой сложный икосододекаэдр можно построить из множества различных вершинных фигур .

Очень похожая фигура возникает как геометрическое усечение большого звездчатого додекаэдра , где грани пентаграммы становятся пятиугольниками с двойной обмоткой ({5/2} --> {10/2}), образуя внутренние пятиугольные плоскости, а три встречающихся в каждой вершине становятся треугольниками, образуя внешние треугольные плоскости.

В качестве соединения

Малый сложный икосододекаэдр можно рассматривать как соединение икосаэдра {5,5/2} , {3,5} и большого додекаэдра где все вершины точны, а ребра совпадают. Малый сложный икосододекаэдр напоминает икосаэдр, поскольку большой додекаэдр полностью содержится внутри икосаэдра.

Составной многогранник

Икосаэдр	Большой додекаэдр	Сложный

Его двумерным аналогом будет соединение правильного пятиугольника {5}, представляющего икосаэдр как n -мерный пятиугольный многогранник , и правильной пентаграммы {5/2}, как n -мерная звезда. Эти фигуры будут иметь общие вершины, подобно тому, как их трехмерный эквивалент имеет общие края.

Составной многоугольник

Пентагон	Пентаграмма	Сложный

См. также

• Большой сложный икосододекаэдр
• Малый сложный ромбокосододекаэдр
• Сложный ромбидодекадодекаэдр
• Большой сложный ромбокосододекаэдр

Ссылки

• Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Серия A. Математические и физические науки , 246 (916): 401–450, Bibcode : 1954RSPTA.246..401C , doi : 10.1098/rsta.1954.0003 , ISSN   0080-4614 , JSTOR   91532 , MR   0062446 , S2CID   202575183 (Таблица 6 , вырожденные случаи)
• Вайсштейн, Эрик В. «Маленький сложный икосододекаэдр» . Математический мир .
• Клитцинг, Ричард. "3D однородные многогранники x3/2o5o5*a - cid" .