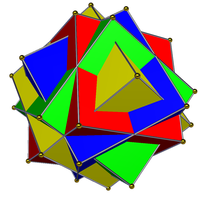
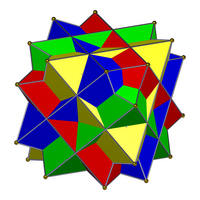
Многогранное соединение

В геометрии многогранником имеющих называется фигура, состоящая из нескольких многогранников, общий центр . Они являются трехмерными аналогами многоугольных соединений, таких как гексаграмма .

Внешние вершины соединения могут быть соединены, образуя выпуклый многогранник, называемый его выпуклой оболочкой . Соединение — это огранка его выпуклой оболочки.

Другой выпуклый многогранник образован небольшим центральным пространством, общим для всех членов соединения. Этот многогранник можно использовать в качестве ядра для набора звездочек .

Регулярные соединения

Правильное многогранное соединение можно определить как соединение, которое, как и правильный многогранник , является транзитивным по вершинам , транзитивным по ребрам и транзитивным по граням . В отличие от случая многогранников, это не эквивалентно тому, что группа симметрии действует транзитивно на свои флаги ; соединение двух тетраэдров — единственное правильное соединение, обладающее таким свойством. Существует пять правильных соединений многогранников:

Обычное соединение (символ Кокстера)	Картина	сферический	Выпуклая оболочка	Общее ядро	Группа симметрии	Подгруппа ограничивающий одному составляющая	Двойное регулярное соединение
Два тетраэдра {4,3}[2{3,3}]{3,4}			Куб	Октаэдр	*432 [4,3] Ой ​	*332 [3,3] Т д	Два тетраэдра
Пять тетраэдров {5,3}[5{3,3}]{3,5}			Додекаэдр	Икосаэдр	532 [5,3] + я	332 [3,3] + Т	Хиральный близнец (энантиоморф)
Десять тетраэдров 2{5,3}[10{3,3}]2{3,5}			Додекаэдр	Икосаэдр	*532 [5,3] I h	332 [3,3] Т	Десять тетраэдров
Пять кубиков 2{5,3}[5{4,3}]			Додекаэдр	Ромбический триаконтаэдр	*532 [5,3] I h	3*2 [3,3] Т ч	Пять октаэдров
Пять октаэдров [5{3,4}]2{3,5}			Икосододекаэдр	Икосаэдр	*532 [5,3] I h	3*2 [3,3] Т ч	Пять кубиков

Наиболее известно правильное соединение двух тетраэдров , часто называемое звездой октангулы , имя, данное ему Кеплером . Вершины двух тетраэдров определяют куб , а их пересечение определяет правильный октаэдр , который имеет те же грани, что и составное соединение. Таким образом, соединение двух тетраэдров есть звёздчатость октаэдра, и фактически единственная его конечная звёздчатость.

Правильное соединение пяти тетраэдров существует в двух энантиоморфных вариантах, которые вместе составляют правильное соединение десяти тетраэдров. Правильное соединение десяти тетраэдров также можно рассматривать как соединение пяти звездочек-октангулов.

Каждое из правильных тетраэдрических соединений самодуально или двойственно своему хиральному двойнику; правильное соединение пяти кубов и правильное соединение пяти октаэдров двойственны друг другу.

Следовательно, правильные многогранные соединения также можно рассматривать как дуально-правильные соединения .

Обозначения Коксетера для регулярных соединений приведены в таблице выше с использованием символов Шлефли . Материал внутри квадратных скобок [ d { p , q } ] обозначает компоненты соединения: d отдельные { p , q }. Материал перед квадратными скобками обозначает расположение вершин соединения: c { m , n } [ d { p , q }] представляет собой соединение d { p , q }, разделяющее подсчитанные вершины { m , n } ц раз. Материал после квадратных скобок обозначает расположение граней соединения: [ d { p , q }] e { s , t } представляет собой соединение d { p , q }, имеющих общие грани { s , t }, посчитанные е раз. Их можно комбинировать: таким образом, c { m , n }[ d { p , q }] e { s , t } представляет собой соединение d { p , q }, разделяющее вершины { m , n }, подсчитанные c раз. и грани { s , t } посчитаны e раз. Эти обозначения можно обобщить на соединения любого количества измерений.

Двойные соединения

Усеченный тетраэдр (светлый) и триакис-тетраэдр (темный)

Курносый куб (светлый) и пятиугольный икоситетраэдр (темный)

Икосододекаэдр (светлый) и ромбический триаконтаэдр (темный)

Двойные соединения архимедовых и каталанских тел.

Двойственное средней соединение состоит из многогранника и его двойника, расположенных взаимно относительно общей сферы , так что ребро одного многогранника пересекает двойственное ребро двойственного многогранника. Существует пять двойственных соединений правильных многогранников.

Ядро – это выпрямление обоих твердых тел. Корпус является двойником этого выпрямления, и его ромбические грани имеют пересекающиеся края двух тел как диагонали (и имеют четыре альтернативные вершины). Для выпуклых тел это выпуклая оболочка .

Двойное соединение	Картина	Халл	Основной	Группа симметрии
Два тетраэдра ( Соединение двух тетраэдров , звездчатый октаэдр )		Куб	Октаэдр	*432 [4,3] Ой ​
Куб и октаэдр ( Соединение куба и октаэдра )		Ромбический додекаэдр	Кубооктаэдр	*432 [4,3] Ой ​
Додекаэдр и икосаэдр ( Соединение додекаэдра и икосаэдра )		Ромбический триаконтаэдр	Икосододекаэдр	*532 [5,3] I h
Малый звездчатый додекаэдр и большой додекаэдр. ( Соединение SD и gD )		Медиальный ромбический триаконтаэдр (Выпуклый: икосаэдр )	Додекадодекаэдр (Выпуклый: додекаэдр )	*532 [5,3] I h
Большой икосаэдр и большой звездчатый додекаэдр. ( Соединение gI и gsD )		Большой ромбический триаконтаэдр (Выпуклый: додекаэдр )	Большой икосододекаэдр (Выпуклый: икосаэдр )	*532 [5,3] I h

Тетраэдр самодуален, поэтому двойственным соединением тетраэдра с его двойником является правильный звездчатый октаэдр .

Октаэдрические и икосаэдрические двойные соединения являются первыми звездчатыми формами кубооктаэдра и икосододекаэдра соответственно.

Двойное соединение малого звездчатого додекаэдра (или большого додекаэдра) имеет большой додекаэдр, полностью расположенный внутри малого звездчатого додекаэдра.

Однородные соединения

Основная статья: Соединение однородного многогранника

В 1976 году Джон Скиллинг опубликовал «Единые соединения однородных многогранников» , в которых перечислил 75 соединений (в том числе 6 как бесконечные призматические наборы соединений, № 20– № 25), состоящих из однородных многогранников с вращательной симметрией. (Каждая вершина является вершинно-транзитивной , и каждая вершина транзитивна по отношению к любой другой вершине.) Этот список включает пять регулярных соединений, приведенных выше. [1]

75 однородных соединений перечислены в таблице ниже. Большинство из них показаны в индивидуальном цвете для каждого элемента многогранника. Некоторые киральные пары групп граней окрашены в зависимости от симметрии граней внутри каждого многогранника.

• 1–19: Разное (4,5,6,9,17 — 5 обычных соединений )

• 20-25: Симметрия призмы, заложенная в симметрию призмы ,

• 26-45: Симметрия призмы, встроенная в октаэдрическую или икосаэдрическую симметрию ,

• 46-67: Тетраэдрическая симметрия, встроенная в октаэдрическую или икосаэдрическую симметрию,

• 68-75: энантиоморфов . пары

Другие соединения

Соединение четырех кубов (слева) не является ни правильным соединением, ни двойственным соединением, ни однородным соединением. Его двойник, соединение четырех октаэдров (справа), представляет собой однородное соединение.

• Соединение трех октаэдров
• Соединение четырех кубиков

Два многогранника, которые являются составными, но элементы которых жестко зафиксированы на месте, — это малый сложный икосододекаэдр (соединение икосаэдра и большого додекаэдра ) и большой сложный икосододекаэдр (соединение малого звездчатого додекаэдра и большого икосаэдра ). Если обобщить определение однородного многогранника , то они однородны.

Раздел пар энантиоморфов в списке Скиллинга не содержит соединения двух больших курносых додецикосододекаэдров , поскольку грани пентаграммы совпадали бы. Удаление совпадающих граней приводит к соединению двадцати октаэдров .

4-многогранные соединения

Ортогональные проекции

75 {4,3,3}	75 {3,3,4}

В 4-мерном измерении существует большое количество правильных соединений правильных многогранников. Коксетер перечисляет некоторые из них в своей книге «Регулярные многогранники» . Макмаллен добавил шесть в своей статье « Новые регулярные соединения 4-многогранников» .

Самодвойственные:

Сложный	Составляющая	Симметрия
120 5-ячеечных	5-клеточный	[5,3,3], порядок 14400
120 5-ячеечных (был)	5-клеточный	заказать 1200
720 5-ячеечных	5-клеточный	[5,3,3], порядок 14400
5 24-ячеечных	24-ячеечный	[5,3,3], порядок 14400

Двойные пары:

Соединение 1	Соединение 2	Симметрия
3 16-ячеечных	3 тессеракта	[3,4,3], порядок 1152
15 16-ячеечных	15 тессерактов	[5,3,3], порядок 14400
75 16-ячеечных	75 тессерактов	[5,3,3], порядок 14400
75 16-ячеечных (был)	75 тессерактов (был)	заказать 600
300 16-ячеечных	300 тессерактов	[5,3,3] + , заказ 7200
600 16-ячеечных	600 тессерактов	[5,3,3], порядок 14400
25 24-клеточных	25 24-клеточных	[5,3,3], порядок 14400

Однородные соединения и дуальные с выпуклыми 4-многогранниками:

Соединение 1 Вершинно-транзитивный	Соединение 2 Клеточно-транзитивный	Симметрия
2 16-ячеечных	2 тессеракта	[4,3,3], порядок 384
100 24-ячеечных	100 24-ячеечных	[5,3,3] + , заказ 7200
200 24-ячеечных	200 24-ячеечных	[5,3,3], порядок 14400
5 600 ячеек	5 120 ячеек	[5,3,3] + , заказ 7200
10 600 ячеек	10 120 ячеек	[5,3,3], порядок 14400
25 24-клеточных (был)	25 24-клеточных (был)	заказать 600

Верхний индекс (var) в таблицах выше указывает на то, что помеченные соединения отличаются от других соединений с таким же количеством компонентов.

Соединения с правильными звездчатыми 4-многогранниками

Самодвойственные звездчатые соединения:

Сложный	Симметрия
5 {5,5/2,5}	[5,3,3] + , заказ 7200
10 {5,5/2,5}	[5,3,3], порядок 14400
5 {5/2,5,5/2}	[5,3,3] + , заказ 7200
10 {5/2,5,5/2}	[5,3,3], порядок 14400

Двойные пары составных звезд:

Соединение 1	Соединение 2	Симметрия
5 {3,5,5/2}	5 {5/2,5,3}	[5,3,3] + , заказ 7200
10 {3,5,5/2}	10 {5/2,5,3}	[5,3,3], порядок 14400
5 {5,5/2,3}	5 {3,5/2,5}	[5,3,3] + , заказ 7200
10 {5,5/2,3}	10 {3,5/2,5}	[5,3,3], порядок 14400
5 {5/2,3,5}	5 {5,3,5/2}	[5,3,3] + , заказ 7200
10 {5/2,3,5}	10 {5,3,5/2}	[5,3,3], порядок 14400

Однородные составные звезды и двойники :

Соединение 1 Вершинно-транзитивный	Соединение 2 Клеточно-транзитивный	Симметрия
5 {3,3,5/2}	5 {5/2,3,3}	[5,3,3] + , заказ 7200
10 {3,3,5/2}	10 {5/2,3,3}	[5,3,3], порядок 14400

Соединения с двойниками

Двойные позиции:

Сложный	Составляющая	Симметрия
2 5-ячеечный	5-клеточный	[[3,3,3]], порядок 240
2 24-ячеечный	24-ячеечный	[[3,4,3]], порядок 2304
1 тессеракт, 1 16-ячеечный	тессеракт , 16 ячеек
1 120 ячеек, 1 600 ячеек	120 ячеек , 600 ячеек
2 отличных 120-ячеечных	отличный 120-ячеечный
2 больших звездчатых 120-ячеечных	большой звездчатый, 120 ячеек
1 икосаэдрический 120-ячеечный, 1 маленький звездчатый 120-ячеечный	икосаэдрический 120-ячеечный , маленький звездчатый 120-ячеечный
1 большой 120-ячеечный, 1 большой звездчатый 120-ячеечный	большой 120-ячеечный , отличный звездчатый 120-ячеечный
1 великий 120-ячеечный, 1 большой икосаэдрический 120-ячеечный.	большой 120-ячеечный великан , большой икосаэдр 120-ячеечный
1 гранд звездчатый на 120 ячеек, 1 великий на 600 ячеек	Большой Гранд звездчатый, 120 ячеек , Гранд, 600 ячеек

Теория групп

С точки зрения теории групп , если G — группа симметрии многогранного соединения, и группа транзитивно действует на многогранники (так что каждый многогранник может быть отправлен в любой из других, как в однородных соединениях), то если H — это Стабилизатор одного выбранного многогранника, многогранники можно отождествить с пространством орбит G / H – смежный класс gH соответствует тому, в какой многогранник g отправляет выбранный многогранник.

Соединения плиток

Существует восемнадцать двухпараметрических семейств правильных составных мозаик евклидовой плоскости. В гиперболической плоскости известны пять однопараметрических семейств и семнадцать единичных случаев, но полнота этого списка не подсчитана.

Евклидовы и гиперболические составные семейства 2 { p , p } (4 ≤ p ≤ ∞, p целое число) аналогичны сферической звезде-октангуле , 2 {3,3}.

Несколько примеров евклидовых и гиперболических правильных соединений.

Самодвойственный	Дуалы		Самодвойственный
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}
	3 {6,3}	3 {3,6}	3 {∞,∞}

Известное семейство правильных евклидовых составных сот в любом количестве измерений представляет собой бесконечное семейство составных гиперкубических сот , все вершины и грани которых имеют общие вершины и грани с другими гиперкубическими сотами. Это соединение может иметь любое количество гиперкубических сот.

Существуют также соединения для плитки с двойной регулярностью . Простой пример — буква E. ² соединение шестиугольной мозаики и ее двойной треугольной мозаики , которая разделяет свои края с дельтовидной тригексагональной мозаикой . Евклидовы соединения двух гиперкубических сот одновременно являются правильными и двойственно правильными.

Внешние ссылки

• MathWorld: Соединение многогранников
• Составные многогранники - из Многогранников виртуальной реальности.
  • Однородные соединения однородных многогранников.
• 75 однородных соединений однородных многогранников Скиллинга.
• Однородные соединения Скиллинга из однородных многогранников.
• Полиэдрические соединения
• http://users.skynet.be/polyhedra.fleurent/Compounds_2/Compounds_2.htm
• Соединение малого звездчатого додекаэдра и большого додекаэдра {5/2,5}+{5,5/2}
• Клитцинг, Ричард. «Составные многогранники» .

Ссылки

• Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, Бибкод : 1976MPCPS..79..447S , doi : 10.1017/S0305004100052440 , MR   039755 4 , S2CID   123279687 .
• Кромвель, Питер Р. (1997), Многогранники , Кембридж {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) .
• Веннингер, Магнус (1983), Двойные модели , Кембридж, Англия: Издательство Кембриджского университета, стр. 51–53 .
• Харман, Майкл Г. (1974), Многогранные соединения , неопубликованная рукопись .
• Гесс, Эдмунд (1876), «Равноугольные и равносторонние многогранники одновременно», публикации Общества содействия естественным наукам в Марбурге , 11 : 5–97 .
• Пачоли, Лука (1509), О божественной пропорции .
• Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8
• Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN  0-520-03056-7 . п. 87 Пять обычных соединений
• МакМаллен, Питер (2018), «Новые регулярные соединения 4-многогранников», Новые тенденции в интуитивной геометрии , Математические исследования Общества Боляи, том. 27, стр. 307–320, номер документа : 10.1007/978-3-662-57413-3_12 , ISBN.  978-3-662-57412-6 .