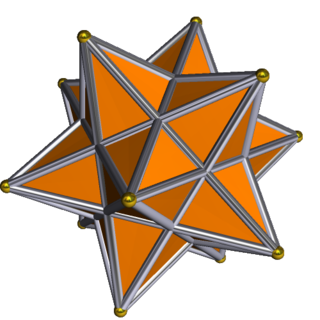
Большой сложный икосододекаэдр

Большой сложный икосододекаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф =32, Е =60 (30х2) V = 12 (χ = -16)
Лица по сторонам	20{3}+12{5/2}
Диаграмма Кокстера
Символ Витхоффа	5 | 3 5/3
Группа симметрии	I h , [5,3], *532
Ссылки на индексы	У - , С - , Ш -
Двойной многогранник	Большой комплекс икосододекакрон
Вершинная фигура	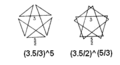(3.5/3) 5 (3.5/2) 5 /3
Аббревиатура Бауэрса	Гасид

В геометрии большой комплексный икосододекаэдр представляет собой вырожденный однородный звездчатый многогранник . У него 12 вершин, 60 (сдвоенных) ребер, 32 грани, 12 пентаграмм и 20 треугольников . Все ребра удваиваются (что делает его вырожденным), имеют четыре грани, но рассматриваются как два перекрывающихся ребра топологического многогранника.

Его можно построить из множества различных фигур вершин .

В качестве соединения

Большой комплексный икосододекаэдр можно рассматривать как соединение малого звездчатого додекаэдра {5/2,5} и большого икосаэдра {3,5/2}, имеющих одни и те же вершины и ребра, тогда как второй скрыт, будучи полностью содержится внутри первого.

Составной многогранник

Малый звездчатый додекаэдр	Большой икосаэдр	Сложный

См. также

• Малый сложный икосододекаэдр
• Малый сложный ромбокосододекаэдр
• Сложный ромбидодекадодекаэдр
• Большой сложный ромбокосододекаэдр

Ссылки

• Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Series A. Mathematical and Physical Sciences , 246 (916): 401–450, doi : 10.1098/rsta.1954.0003 , ISSN   0080-4614 , JSTOR   91532 , MR   0062446 , S2CID   202575183 (Таблица 6, вырожденные случаи)
• Вайсштейн, Эрик В. «Большой сложный икосододекаэдр» . Математический мир .
• Клитцинг, Ричард. «3D однородные многогранники о5/3х3о5*а и о3/2х5/2о5*а - гацид» .