Списки однородных мозаик на сфере, плоскости и гиперболической плоскости.

В геометрии многие однородные мозаики на сфере, евклидовой плоскости и гиперболической плоскости могут быть созданы с помощью конструкции Витхоффа внутри фундаментального треугольника (pqr), определяемого внутренними углами как π/p, π/q и π/r. Особыми случаями являются прямоугольные треугольники (pq 2). Равномерные решения строятся с помощью одной образующей точки с 7 позициями внутри основного треугольника, 3 углов, вдоль 3 ребер и внутри треугольника. Все вершины существуют в генераторе или в его отраженной копии. Между точкой генератора и ее изображением в зеркале существуют ребра. Существует до трех типов лиц, центрированных по основным углам треугольника. Домены прямоугольных треугольников могут иметь всего один тип граней, образуя правильные формы, в то время как обычные треугольники имеют как минимум два типа треугольников, что в лучшем случае приводит к квазирегулярной мозаике.

Существуют разные обозначения для выражения этих равномерных решений: символ Витхоффа , диаграмма Кокстера и t-нотация Коксетера.

Простые плитки генерируются треугольниками Мёбиуса с целыми числами p,q,r, тогда как треугольники Шварца допускают рациональные числа p,q,r, допускают грани звездчатых многоугольников и имеют перекрывающиеся элементы.

7 очков генератора

Семь генераторных точек с каждым набором $p,q,r$ (и несколько специальных форм):

Общий				Прямоугольный треугольник (r=2)
Описание	Витхофф символ	Вертекс конфигурация	Коксетер диаграмма	Витхофф символ	Вертекс конфигурация	Шлефли символ		Коксетер диаграмма
регулярный и квазирегулярный	д | пиар	( п . р ) д		д | п 2	п д	{п, д}
	р | qr	( д . р ) п		р | q 2	д п	{д, р}
	р | ПК	( д . п ) р		2 | ПК	( q . p )²	г {р, q}	т 1 {p,q}
усечено и расширенный	qр | п	⁠ $q.2p.r.2p$⁠		д 2 | п	⁠ $q.2p.2p$⁠	t{p,q}	т 0,1 {p,q}
	пр | д	⁠ $p.2q.r.2q$⁠		р 2 | д	п . 2 кв .2 кв	т{q,p}	т 0,1 {q,p}
	ПК | р	⁠ $2r.q.2r.p$⁠		ПК | 2	⁠ $4.q.4.p$⁠	rr{p,q}	т 0,2 {p,q}
беспристрастный	пкр |	⁠ $2r.2q.2p$⁠		кв 2 |	⁠ $4.2q.2p$⁠	tr{p,q}	т 0,1,2 {p,q}
	pq ( rs ) |	⁠ $2p.2q.-2p.-2q$⁠	-	п 2 ( рс ) |	2 п.4. -2 п . 4 / 3			-
пренебрегать	| пкр	⁠ $3.r.3.q.3.p$⁠		| ПК 2	⁠ $3.3.q.3.p$⁠	ср{п,q}
	| пкр с	⁠ $(4.p.4.q.4.r.4.s)/2$⁠	-	-	-			-

Есть три особых случая:

• $p\ q\ (r\ s)\ |$ – Это смесь $p\ q\ r\ |$ и $p\ q\ s\ |$, содержащий только общие лица обоих.
• $|\ p\ q\ r$ – Курносые формы (чередующиеся) обозначаются этим неиспользуемым символом.
• $|\ p\ q\ r\ s$ – Уникальная укороченная форма для U75 , не подходящая для конструкции Wythoff.

Симметрия треугольников

имеется 4 класса симметрии отражения На сфере , а на евклидовой плоскости - три . некоторые из бесконечного множества таких шаблонов в гиперболической плоскости Также перечислены . (Увеличение любого числа, определяющего гиперболическую или евклидову мозаику, приводит к созданию другой гиперболической мозаики.)

Группы точек:

• (p 2 2) диэдральная симметрия , $p=2,3,4\dots$ (заказ $4p$)
• (3 3 2) тетраэдрическая симметрия (порядок 24)
• (4 3 2) октаэдрическая симметрия (порядок 48)
• (5 3 2) икосаэдрическая симметрия (порядок 120)

Евклидовы (аффинные) группы:

• (4 4 2) *442 симметрия : треугольник 45°-45°-90°
• (6 3 2) * 632 симметрия : треугольник 30°-60°-90°
• (3 3 3) * 333 симметрия : треугольник 60°-60°-60°

Гиперболические группы:

• (7 3 2) * 732 симметрия
• (8 3 2) * 832 симметрия
• (4 3 3) * 433 симметрия
• (4 4 3) * 443 симметрия
• (4 4 4) * 444 симметрия
• (5 4 2) * 542 симметрия
• (6 4 2) * 642 симметрия
• ...

Двугранный сферический					сферический
Д 2 часа	Д 3 часа	Д 4 часа	Д 5ч	Д 6ч	Т д	Ой ​	I h
*222	*322	*422	*522	*622	*332	*432	*532
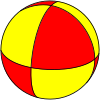(2 2 2)	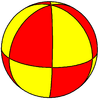(3 2 2)	(4 2 2)	(5 2 2)	(6 2 2)	(3 3 2)	(4 3 2)	(5 3 2)

Вышеупомянутые группы симметрии включают только целочисленные решения на сфере. Список треугольников Шварца включает рациональные числа и определяет полный набор решений невыпуклых однородных многогранников .

Евклидова плоскость

п4м	п3м	п6м
*442	*333	*632
(4 4 2)	(3 3 3)	(6 3 2)

Гиперболическая плоскость

*732	*542	*433
(7 3 2)	(5 4 2)	(4 3 3)

В приведенных выше мозаиках каждый треугольник представляет собой фундаментальную область, окрашенную четными и нечетными отражениями.

Суммарные сферические, евклидовы и гиперболические мозаики

Ниже приведены избранные мозаики, созданные с помощью конструкции Витгофа.

Сферические мозаики ( r = 2)

(пк 2)	Родитель	Усечено	Исправленный	Битусеченный	биректифицированный (двойной)	Отмененный	Всеусеченный ( Количественно усечено )	пренебрежительный
Витхофф символ	д | п 2	2 кв | п	2 | ПК	2 р | д	р | q 2	ПК | 2	кв 2 |	| ПК 2
Шлефли символ	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{п, д}	t{p,q}	г {р, q}	т{q,p}	{д, р}	rr{p,q}	tr{p,q}	ср{п,q}
	т 0 {p,q}	т 0,1 {p,q}	т 1 {p,q}	т 1,2 {p,q}	т 2 {p,q}	т 0,2 {p,q}	т 0,1,2 {p,q}
Коксетер диаграмма
Вершинная фигура	п д	q.2p.2p	(пк) 2	п. 2кв.2кв	д п	п. 4.q.4	4.2п.2к	3.3.п. 3.q
(3 3 2)	{3,3}	(3.6.6)	(3.3а.3.3а)	(3.6.6)	{3,3}	(3а.4.3б.4)	(4.6а.6б)	(3.3.3а.3.3б)
(4 3 2)	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4а.4)	(4.6.8)	(3.3.3а.3.4)
(5 3 2)	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3а.3.5)

Некоторые перекрывающиеся сферические мозаики ( r = 2)

Более полный список, включая случаи, когда r ≠ 2, см. в разделе Список однородных многогранников по треугольнику Шварца .

Тайлинги изображаются в виде многогранников . Некоторые формы являются вырожденными, заданными скобками для фигур вершин , с перекрывающимися ребрами или вершинами.

(пк 2)	Фонд. треугольник	Родитель	Усечено	Исправленный	Битусеченный	биректифицированный (двойной)	Отмененный	Всеусеченный ( Количественно усечено )	пренебрежительный
Символ Витхоффа		д | п 2	2 кв | п	2 | ПК	2 р | д	р | q 2	ПК | 2	кв 2 |	| ПК 2
Символ Шлефли		${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
		{п, д}	t{p,q}	г {р, q}	т{q,p}	{д, р}	rr{p,q}	tr{p,q}	ср{п,q}
		т 0 {p,q}	т 0,1 {p,q}	т 1 {p,q}	т 1,2 {p,q}	т 2 {p,q}	т 0,2 {p,q}	т 0,1,2 {p,q}
Диаграмма Кокстера – Дынкина
Вершинная фигура		п д	(к.2п.2п)	(пкпк)	(стр. 2q.2q)	д п	(п. 4.q.4)	(4.2п.2к)	(3.3.п. 3.q)
икосаэдрический (5/2 3 2)		{3,5/2}	(5/2.6.6)	(3.5/2) 2	[3.10/2.10/2]	{5/2,3}	[3.4.5/2.4]	[4.10/2.6]	(3.3.3.3.5/2)
икосаэдрический (5 5/2 2)		{5,5/2}	(5/2.10.10)	(5/2.5) 2	[5.10/2.10/2]	{5/2,5}	(5/2.4.5.4)	[4.10/2.10]	(3.3.5/2.3.5)

Диэдральная симметрия ( q = r = 2)

Сферические мозаики с двугранной симметрией существуют для всех $p=2,3,4,\dots$ многие из них имеют двуугольные грани, которые превращаются в вырожденные многогранники. Две из восьми форм (ректифицированная и кантиллированная) являются повторами и в таблице пропущены.

(п 2 2) Фундаментальный домен	Родитель	Усечено	Битусеченный (усеченный двойной)	биректифицированный (двойной)	Всеусеченный ( Количественно усечено )	пренебрежительный
Расширенный Символ Шлефли	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{п, 2}	т{р,2}	т{2,р}	{2,р}	тр{п,2}	ср{п,2}
	т 0 {р,2}	т 0,1 {р,2}	т 1,2 {п,2}	т 2 {р,2}	т 0,1,2 {р,2}
Символ Витхоффа	2 | п 2	2 2 | п	2 р | 2	р | 2 2	р 2 2 |	| п 2 2
Диаграмма Кокстера – Дынкина
Вершинная фигура	р²	(2.2п.2п)	(4.4.п)	2 п	(4.2п.4)	(3.3.п. 3)
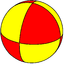(2 2 2) Версия 2.2.2	{2,2}	2.4.4	4.4.2	{2,2}	4.4.4	3.3.3.2
(3 2 2) Версия 3.2.2	{3,2}	2.6.6	4.4.3	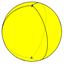{2,3}	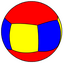4.4.6	3.3.3.3
(4 2 2) Версия 4.2.2	{4,2}	2.8.8	4.4.4	{2,4}	4.4.8	3.3.3.4
(5 2 2) Версия 5.2.2	{5,2}	2.10.10	4.4.5	{2,5}	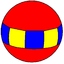4.4.10	3.3.3.5
(6 2 2) Версия 6.2.2	{6,2}	2.12.12	4.4.6	{2,6}	4.4.12	3.3.3.6
...

Евклидовы и гиперболические мозаики ( r = 2)

Даны некоторые типичные гиперболические мозаики, которые показаны в виде проекции диска Пуанкаре .

(пк 2)	Фонд. треугольники	Родитель	Усечено	Исправленный	Битусеченный	биректифицированный (двойной)	Отмененный	Всеусеченный ( Количественно усечено )	пренебрежительный
Символ Витхоффа		д | п 2	2 кв | п	2 | ПК	2 р | д	р | q 2	ПК | 2	кв 2 |	| ПК 2
Символ Шлефли		${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
		{п, д}	t{p,q}	г {р, q}	т{q,p}	{д, р}	rr{p,q}	tr{p,q}	ср{п,q}
		т 0 {p,q}	т 0,1 {p,q}	т 1 {p,q}	т 1,2 {p,q}	т 2 {p,q}	т 0,2 {p,q}	т 0,1,2 {p,q}
Диаграмма Кокстера – Дынкина
Вершинная фигура		п д	(к.2п.2п)	(пкпк)	(стр. 2q.2q)	д п	(п. 4.q.4)	(4.2п.2к)	(3.3.п. 3.q)
Шестиугольная плитка (6 3 2)	Версия 4.6.12	{6,3}	3.12.12	3.6.3.6	6.6.6	{3,6}	3.4.6.4	4.6.12	3.3.3.3.6
(Гиперболическая плоскость) (7 3 2)	Версия 4.6.14	{7,3}	3.14.14	3.7.3.7	7.6.6	{3,7}	3.4.7.4	4.6.14	3.3.3.3.7
(Гиперболическая плоскость) (8 3 2)	В4.6.16	{8,3}	3.16.16	3.8.3.8	8.6.6	{3,8}	3.4.8.4	4.6.16	3.3.3.3.8
Квадратная плитка (4 4 2)	Версия 4.8.8	{4,4}	4.8.8	4.4а.4.4а	4.8.8	{4,4}	4.4а.4б.4а	4.8.8	3.3.4а.3.4б
(Гиперболическая плоскость) (5 4 2)	Версия 4.8.10	{5,4}	4.10.10	4.5.4.5	5.8.8	{4,5}	4.4.5.4	4.8.10	3.3.4.3.5
(Гиперболическая плоскость) (6 4 2)	Версия 4.8.12	{6,4}	4.12.12	4.6.4.6	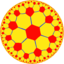6.8.8	{4,6}	4.4.6.4	4.8.12	3.3.4.3.6
(Гиперболическая плоскость) (7 4 2)	Версия 4.8.14	{7,4}	4.14.14	4.7.4.7	7.8.8	{4,7}	4.4.7.4	4.8.14	3.3.4.3.7
(Гиперболическая плоскость) (8 4 2)	В4.8.16	{8,4}	4.16.16	4.8.4.8	8.8.8	{4,8}	4.4.8.4	4.8.16	3.3.4.3.8
(Гиперболическая плоскость) (5 5 2)	В4.10.10	{5,5}	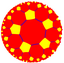5.10.10	5.5.5.5	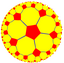5.10.10	{5,5}	5.4.5.4	4.10.10	3.3.5.3.5
(Гиперболическая плоскость) (6 5 2)	В4.10.12	{6,5}	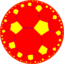5.12.12	5.6.5.6	6.10.10	{5,6}	5.4.6.4	4.10.12	3.3.5.3.6
(Гиперболическая плоскость) (7 5 2)	В4.10.14	{7,5}	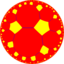5.14.14	5.7.5.7	7.10.10	{5,7}	5.4.7.4	4.10.14	3.3.5.3.7
(Гиперболическая плоскость) (8 5 2)	В4.10.16	{8,5}	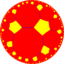5.16.16	5.8.5.8	8.10.10	{5,8}	5.4.8.4	4.10.16	3.3.5.3.8
(Гиперболическая плоскость) (6 6 2)	В4.12.12	{6,6}	6.12.12	6.6.6.6	6.12.12	{6,6}	6.4.6.4	4.12.12	3.3.6.3.6
(Гиперболическая плоскость) (7 6 2)	В4.12.14	{7,6}	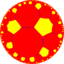6.14.14	6.7.6.7	7.12.12	{6,7}	6.4.7.4	4.12.14	3.3.6.3.7
(Гиперболическая плоскость) (8 6 2)	В4.12.16	{8,6}	6.16.16	6.8.6.8	8.12.12	{6,8}	6.4.8.4	4.12.16	3.3.6.3.8
(Гиперболическая плоскость) (7 7 2)	В4.14.14	{7,7}	7.14.14	7.7.7.7	7.14.14	{7,7}	7.4.7.4	4.14.14	3.3.7.3.7
(Гиперболическая плоскость) (8 7 2)	В4.14.16	{8,7}	7.16.16	7.8.7.8	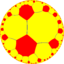8.14.14	{7,8}	7.4.8.4	4.14.16	3.3.7.3.8
(Гиперболическая плоскость) (8 8 2)	В4.16.16	{8,8}	8.16.16	8.8.8.8	8.16.16	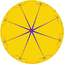{8,8}	8.4.8.4	4.16.16	3.3.8.3.8
(Гиперболическая плоскость) (∞ 3 2)	V4.6.∞	{∞,3}	3.∞.∞	3.∞.3.∞	∞.6.6	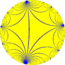{3,∞}	3.4.∞.4	4.6.∞	3.3.3.3.∞
(Гиперболическая плоскость) (∞ 4 2)	V4.8.∞	{∞,4}	4.∞.∞	4.∞.4.∞	∞.8.8	{4,∞}	4.4.∞.4	4.8.∞	3.3.4.3.∞
(Гиперболическая плоскость) (∞ 5 2)	V4.10.∞	{∞,5}	5.∞.∞	5.∞.5.∞	∞.10.10	{5,∞}	5.4.∞.4	4.10.∞	3.3.5.3.∞
(Гиперболическая плоскость) (∞ 6 2)	V4.12.∞	{∞,6}	6.∞.∞	6.∞.6.∞	∞.12.12	{6,∞}	6.4.∞.4	4.12.∞	3.3.6.3.∞
(Гиперболическая плоскость) (∞ 7 2)	V4.14.∞	{∞,7}	7.∞.∞	7.∞.7.∞	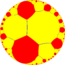∞.14.14	{7,∞}	7.4.∞.4	4.14.∞	3.3.7.3.∞
(Гиперболическая плоскость) (∞ 8 2)	V4.16.∞	{∞,8}	8.∞.∞	8.∞.8.∞	∞.16.16	{8,∞}	8.4.∞.4	4.16.∞	3.3.8.3.∞
(Гиперболическая плоскость) (∞ ∞ 2)	V4.∞.∞	{∞,∞}	∞.∞.∞	∞.∞.∞.∞	∞.∞.∞	{∞,∞}	∞.4.∞.4	4.∞.∞	3.3.∞.3.∞

Евклидовы и гиперболические мозаики ( r > 2)

Диаграмма Коксетера – Дынкина представлена ​​в линейной форме, хотя на самом деле она представляет собой треугольник, конечный отрезок r которого соединяется с первым узлом.

Символ Витхоффа (pqr)	Фонд. треугольники	д | пиар	rq | п	р | ПК	рп | д	р | qr	ПК | р	пкр |	| пкр
Символ Шлефли		(п, д, г)	г (г, д, р)	(д, г, р)	г (р, q, г)	(д, п, г)	г (р, г, q)	tr(p,q,r)	s(p,q,r)
		т 0 (p,q,r)	t 0,1 (p,q,r)	т 1 (p,q,r)	t 1,2 (p,q,r)	т 2 (p,q,r)	t 0,2 (p,q,r)	т 0,1,2 (p,q,r)
Диаграмма Кокстера
Вершинная фигура		(пр) д	(r.2p.q.2p)	(пк) р	(р. 2д.п. 2д)	(qr) п	(стр. 2р.к.2р)	(2п.2к.2р)	(3.r.3.q.3.p)
евклидов (3 3 3)	Версия 6.6.6	(3.3) 3	3.6.3.6	(3.3) 3	3.6.3.6	(3.3) 3	3.6.3.6	6.6.6	3.3.3.3.3.3
гиперболический (4 3 3)	Версия 6.6.8	(3.4) 3	3.8.3.8	(3.4) 3	3.6.4.6	(3.3) 4	3.6.4.6	6.6.8	3.3.3.3.3.4
гиперболический (4 4 3)	Версия 6.8.8	(3.4) 4	3.8.4.8	(4.4) 3	3.8.4.8	(3.4) 4	4.6.4.6	6.8.8	3.3.3.4.3.4
гиперболический (4 4 4)	Версия 8.8.8	(4.4) 4	4.8.4.8	(4.4) 4	4.8.4.8	(4.4) 4	4.8.4.8	8.8.8	3.4.3.4.3.4
гиперболический (5 3 3)	Версия 6.6.10	(3.5) 3	3.10.3.10	(3.5) 3	3.6.5.6	(3.3) 5	3.6.5.6	6.6.10	3.3.3.3.3.5
гиперболический (5 4 3)	Версия 6.8.10	(3.5) 4	3.10.4.10	(4.5) 3	3.8.5.8	(3.4) 5	4.6.5.6	6.8.10	3.5.3.4.3.3
гиперболический (5 4 4)	Версия 8.8.10	(4.5) 4	4.10.4.10	(4.5) 4	4.8.5.8	(4.4) 5	4.8.5.8	8.8.10	3.4.3.4.3.5
гиперболический (6 3 3)	Версия 6.6.12	(3.6) 3	3.12.3.12	(3.6) 3	3.6.6.6	(3.3) 6	3.6.6.6	6.6.12	3.3.3.3.3.6
гиперболический (6 4 3)	Версия 6.8.12	(3.6) 4	3.12.4.12	(4.6) 3	3.8.6.8	(3.4) 6	4.6.6.6	6.8.12	3.6.3.4.3.3
гиперболический (6 4 4)	В8.8.12	(4.6) 4	4.12.4.12	(4.6) 4	4.8.6.8	(4.4) 6	4.8.6.8	8.8.12	3.6.3.4.3.4
гиперболический (∞ 3 3)	V6.6.∞	(3.∞) 3	3.∞.3.∞	(3.∞) 3	3.6.∞.6	(3.3) ∞	3.6.∞.6	6.6.∞	3.3.3.3.3.∞
гиперболический (∞ 4 3)	V6.8.∞	(3.∞) 4	3.∞.4.∞	(4.∞) 3	3.8.∞.8	(3.4) ∞	4.6.∞.6	6.8.∞	3.∞.3.4.3.3
гиперболический (∞ 4 4)	V8.8.∞	(4.∞) 4	4.∞.4.∞	(4.∞) 4	4.8.∞.8	(4.4) ∞	4.8.∞.8	8.8.∞	3.∞.3.4.3.4
гиперболический (∞ ∞ 3)	V6.∞.∞	(3.∞) ∞	3.∞.∞.∞	(∞.∞) 3	3.∞.∞.∞	(3.∞) ∞	∞.6.∞.6	6.∞.∞	3.∞.3.∞.3.3
гиперболический (∞ ∞ 4)	V8.∞.∞	(4.∞) ∞	4.∞.∞.∞	(∞.∞) 4	4.∞.∞.∞	(4.∞) ∞	∞.8.∞.8	8.∞.∞	3.∞.3.∞.3.4
гиперболический (∞ ∞ ∞)	V∞.∞.∞	(∞.∞) ∞	∞.∞.∞.∞	(∞.∞) ∞	∞.∞.∞.∞	(∞.∞) ∞	∞.∞.∞.∞	∞.∞.∞	3.∞.3.∞.3.∞

См. также

• Правильный многогранник
• Правильный многогранник
• Список однородных мозаик
• Равномерные мозаики в гиперболической плоскости
• Список однородных многогранников
• Список однородных многогранников по треугольнику Шварца

Ссылки

• Кокстера Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN   0-486-61480-8 (Глава V: Калейдоскоп, раздел: 5.7 Конструкция Витхоффа)
• Коксетер Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN   0-486-40919-8 (Глава 3: Конструкция Витхоффа для однородных многогранников)
• Коксетер , Лонге-Хиггинс, Миллер, Равномерные многогранники , Фил. Пер. 1954, 246 А, 401–50.
• Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN  0-521-09859-9 . стр. 9–10.

Внешние ссылки

• Вайсштейн, Эрик В. «Символ Витхоффа» . Математический мир .
• Символ Витхоффа
• Апплет Грега Игана для отображения однородных многогранников с использованием метода построения Витхоффа.
• Рендеринг метода строительства Витхоффа в Shadertoy.
• KaleidoTile 3 Бесплатное образовательное программное обеспечение для Windows от Джеффри Уикса , с помощью которого было создано множество изображений на странице.
• Хэтч, Дон. «Гиперболические плоские мозаики» .