Секстическое уравнение

График секстической функции с 6 действительными корнями (пересечениями оси x ) и 5 ​​критическими точками . В зависимости от количества и вертикального расположения минимумов и максимумов секстик может иметь 6, 4, 2 или не иметь действительных корней. Количество комплексных корней равно 6 минус количество действительных корней.

В алгебре секстический — (или шестнадцатеричный ) многочлен это многочлен степени шестой . Секстическое уравнение — это полиномиальное уравнение шестой степени, то есть уравнение , левая часть которого представляет собой секстический полином, а правая часть равна нулю. Точнее, оно имеет вид:

$ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\,$

где a ≠ 0 и коэффициенты a , b , c , d , e , f , g могут быть целыми числами , рациональными числами , действительными числами , комплексными числами или, в более общем плане, членами любого поля .

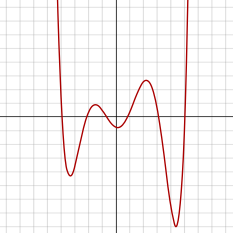
Секстическая функция — это функция, определяемая секстическим полиномом. Поскольку секстические функции имеют четную степень, на графике они кажутся похожими на функции квартичной степени , за исключением того, что каждая из них может иметь дополнительный локальный максимум и локальный минимум. Производная функцией секстической функции является квинтики .

Поскольку секстическая функция определяется полиномом четной степени, она имеет один и тот же бесконечный предел, когда аргумент переходит в положительную или отрицательную бесконечность . Если старший коэффициент a положителен, то функция возрастает до положительной бесконечности с обеих сторон и, таким образом, функция имеет глобальный минимум. Аналогично, если a отрицательно, секстическая функция уменьшается до отрицательной бесконечности и имеет глобальный максимум.

Разрешимые секстики

Некоторые уравнения шестой степени, такие как ax ⁶ + дх ³ + g = 0 , можно решить путем разложения на радикалы, но другие секстики — нет. Эварист Галуа разработал методы определения того, может ли данное уравнение быть решено с помощью радикалов, что привело к возникновению области теории Галуа .

Из теории Галуа следует, что секстическое уравнение разрешимо в терминах радикалов тогда и только тогда, когда его группа Галуа содержится либо в группе порядка 48, стабилизирующей разбиение множества корней на три подмножества по два корня, либо в группе группа порядка 72, которая стабилизирует разбиение множества корней на два подмножества по три корня.

Существуют формулы, позволяющие проверить любой случай и, если уравнение разрешимо, вычислить корни через радикалы.

Общее секстическое уравнение можно решить с помощью функции Кампе де Ферье с двумя переменными . Более ограниченный класс секстиков может быть решен с помощью обобщенной гипергеометрической функции с одной переменной, используя Феликса Кляйна подход к решению уравнения пятой степени .

Примеры

Кривая Ватта , возникшая в контексте ранних работ над паровым двигателем , представляет собой секстик двух переменных.

Один из методов решения кубического уравнения включает преобразование переменных для получения секстического уравнения, имеющего члены только степеней 6, 3 и 0, которое можно решить как квадратное уравнение в кубе переменной.

Этимология

Описатель «секстик» происходит от латинской основы , обозначающей 6 или 6-й («секс-т-»), и греческого суффикса, означающего «относящийся к» («-ic»). Гораздо менее распространенный «гексик» использует греческий язык как для своей основы ( hex- 6), так и для суффикса ( -ik- ). В обоих случаях префикс относится к степени функции. Часто функции такого типа называют просто «функциями 6-й степени».

См. также

• Секстик Кейли
• Кубическая функция
• Септическое уравнение