Кубическая функция

Не путать с кубическим уравнением .

График кубической функции с тремя действительными корнями (где кривая пересекает горизонтальную ось — где y = 0 ). Показанный случай имеет две критические точки . Здесь функция f ( x ) = ( x ³ + 3x ² - 6 Икс - 8)/4 .

В математике кубическая функция — это функция вида $f(x)=ax^{3}+bx^{2}+cx+d,$ то есть полиномиальная функция третьей степени. Во многих текстах коэффициенты a , b , c и d должны быть действительными числами , а функция рассматривается как действительная функция , которая отображает действительные числа в действительные числа, или как комплексная функция, которая отображает комплексные числа в комплексные числа. которой является набор комплексных чисел В других случаях коэффициенты могут быть комплексными числами, а функция является комплексной функцией, кодом , даже если область определения ограничена действительными числами.

Установка f ( x ) = 0 дает кубическое уравнение формы

$ax^{3}+bx^{2}+cx+d=0,$

решения которого называются корнями функции. Производная квадратичной кубической функции является функцией .

Кубическая функция с действительными коэффициентами имеет один или три действительных корня ( которые могут не быть различными ); все полиномы нечетной степени с действительными коэффициентами имеют хотя бы один действительный корень.

График кубической функции всегда имеет одну точку перегиба . Он может иметь две критические точки : локальный минимум и локальный максимум. В противном случае кубическая функция монотонна . График кубической функции симметричен относительно точки перегиба; то есть он инвариантен относительно поворота на пол-оборота вокруг этой точки. С точностью до аффинного преобразования возможны только три графика кубических функций.

Кубические функции являются фундаментальными для кубической интерполяции .

История

Основная статья: Кубическое уравнение § История

и

Корни точка , точки покоя , перегиба и вогнутость кубического многочлена x ³ − 6x ² + 9 x − 4 (сплошная черная кривая) и ее первая (пунктирная красная) и вторая (пунктирная оранжевая) производные .

Критические точки кубической функции — это ее стационарные точки , то есть точки, в которых наклон функции равен нулю. Таким образом, критические точки кубической функции f, определяемой формулой

ж ( Икс ) = топор ³ + бх ² + сх + д ,

происходят при таких значениях x , что производная

$3ax^{2}+2bx+c=0$

кубической функции равна нулю.

Решениями этого уравнения являются значения x критических точек, которые определяются по формуле квадратичной

$x_{\text{critical}}={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.$

Знак выражения Δ ₀ = b ² – 3 ак внутри квадратного корня определяют количество критических точек. Если оно положительное, то имеются две критические точки: одна — локальный максимум, другая — локальный минимум. Если б ² – 3 ac = 0 , то существует только одна критическая точка, которая является точкой перегиба . Если б ² – 3 ac < 0 , то (реальных) критических точек нет. В двух последних случаях, то есть если b ² – 3 ac неположительна, кубическая функция строго монотонна . На рисунке показан пример случая Δ ₀ > 0 .

Точка перегиба функции — это место, где эта функция меняет вогнутость . Точка перегиба возникает, когда вторая производная $f''(x)=6ax+2b,$ равно нулю, а третья производная не равна нулю. Таким образом, кубическая функция всегда имеет одну точку перегиба, которая возникает при

$x_{\text{inflection}}=-{\frac {b}{3a}}.$

Классификация

Кубические функции вида $y=x^{3}+cx.$
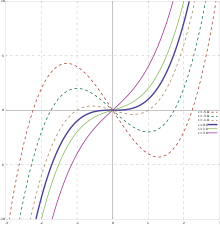
График любой кубической функции подобен такой кривой.

График , кубической функции представляет собой кубическую кривую хотя многие кубические кривые не являются графиками функций.

Хотя кубические функции зависят от четырех параметров, их график может иметь очень мало форм. В действительности график кубической функции всегда подобен графику функции вида

$y=x^{3}+px.$

Это подобие можно построить как композицию сдвигов, параллельных осям координат, гомотезии ( равномерного масштабирования ) и, возможно, отражения ( зеркального отображения ) относительно оси y . Дальнейшее неравномерное масштабирование может превратить график в график одной из трех кубических функций.

${\begin{aligned}y&=x^{3}+x\\y&=x^{3}\\y&=x^{3}-x.\end{aligned}}$

Это означает, что существует только три графика кубических функций с точностью до аффинного преобразования .

Приведенные выше геометрические преобразования можно построить следующим образом, исходя из общей кубической функции $y=ax^{3}+bx^{2}+cx+d.$

Во-первых, если a < 0 , то замена переменной x → – x позволяет предположить a > 0 . После этой замены переменной новый график является зеркальным отображением предыдущего относительно оси y .

Тогда замена переменной x = x ₁ – б / 3а обеспечивает функцию вида

$y=ax_{1}^{3}+px_{1}+q.$

Это соответствует перемещению параллельно оси x .

Замена переменной y = y ₁ + q соответствует сдвигу относительно оси y и дает функцию вида

$y_{1}=ax_{1}^{3}+px_{1}.$

Изменение переменной $\textstyle x_{1}={\frac {x_{2}}{\sqrt {a}}},y_{1}={\frac {y_{2}}{\sqrt {a}}}$ соответствует равномерному масштабированию и дает после умножения на ${\sqrt {a}},$ функция формы

$y_{2}=x_{2}^{3}+px_{2},$

что является простейшей формой, которую можно получить путем подобия.

Тогда, если p ≠ 0 , неравномерное масштабирование $\textstyle x_{2}=x_{3}{\sqrt {|p|}},\quad y_{2}=y_{3}{\sqrt {|p|^{3}}}$ дает после деления на $\textstyle {\sqrt {|p|^{3}}},$

$y_{3}=x_{3}^{3}+x_{3}\operatorname {sgn}(p),$

где $\operatorname {sgn}(p)$ имеет значение 1 или –1, в зависимости от знака p . Если определить $\operatorname {sgn}(0)=0,$ последняя форма функции применима во всех случаях (при $x_{2}=x_{3}$ и $y_{2}=y_{3}$).

Симметрия

Для кубической функции вида $y=x^{3}+px,$ точка перегиба, таким образом, является началом координат. Поскольку такая функция является нечетной функцией , ее график симметричен относительно точки перегиба и инвариантен относительно поворота на пол-оборота вокруг точки перегиба. Поскольку эти свойства инвариантны по подобию , для всех кубических функций верно следующее.

График кубической функции симметричен относительно точки перегиба и инвариантен относительно поворота на пол-оборота вокруг точки перегиба.

Коллинеарности

Точки P1 _, одной P2 _. и P3 _{(синего цвета) лежат на} прямой и принадлежат графику x ³ + 3/2 2х ² − 5/2 ​ ​ х + 5 / 4 . Точки T ₁ , T ₂ и T ₃ (красные) являются пересечениями (пунктирных) касательных к графику в этих точках с самим графиком. Они тоже коллинеарны.

Касательные линии к графику кубической функции в трех коллинеарных точках снова пересекают кубическую функцию в коллинеарных точках. Это можно увидеть следующим образом.

Поскольку это свойство инвариантно относительно жесткого движения , можно предположить, что функция имеет вид

$f(x)=x^{3}+px.$

Если α — действительное число, то касательная к графику f в точке ( α , f ( α )) — это прямая

{( Икс , ж ( α ) + ( Икс - α ) ж ′ ( α )) : Икс ∈ R }.

Итак, точку пересечения этой линии и графика f можно получить, решив уравнение f ( x ) = f ( α ) + ( x − α ) f ′( α ) , то есть

$x^{3}+px=\alpha ^{3}+p\alpha +(x-\alpha )(3\alpha ^{2}+p),$

который можно переписать

$x^{3}-3\alpha ^{2}x+2\alpha ^{3}=0,$

и факторизован как

$(x-\alpha )^{2}(x+2\alpha )=0.$

Итак, касательная пересекает кубическую в точке

$(-2\alpha ,-8\alpha ^{3}-2p\alpha )=(-2\alpha ,-8f(\alpha )+6p\alpha ).$

Итак, функция, которая сопоставляет точку ( x , y ) графика с другой точкой, где касательная пересекает график, равна

$(x,y)\mapsto (-2x,-8y+6px).$

Это аффинное преобразование , которое преобразует коллинеарные точки в коллинеарные точки. Это подтверждает заявленный результат.

Кубическая интерполяция

Основная статья: Сплайн-интерполяция

Учитывая значения функции и ее производной в двух точках, существует ровно одна кубическая функция, имеющая одинаковые четыре значения, которая называется кубическим сплайном Эрмита .

Есть два стандартных способа использования этого факта. Во-первых, если известны, например, посредством физического измерения, значения функции и ее производной в некоторых точках выборки, можно интерполировать функцию с помощью непрерывно дифференцируемой функции , которая является кусочно -кубической функцией.

Если значение функции известно в нескольких точках, кубическая интерполяция состоит в приближении функции непрерывно дифференцируемой функцией , которая является кусочно- кубичной. Для однозначного определения интерполяции необходимо добавить еще два ограничения, например значения производных в конечных точках или нулевую кривизну в конечных точках.

Внешние ссылки

• «Формула Кардано» , Математическая энциклопедия , EMS Press , 2001 [1994]
• История квадратных, кубических и четвертых уравнений в архиве MacTutor .