Квадратичная формула

Не путать с квадратичной функцией или квадратным уравнением .

Корни квадратичной функции y = 1/2 2х ² − 3 х + 5/2 — 5 это места пересечения графика с осью x , значения x = 1 и x = . Их можно найти по квадратичной формуле.

В элементарной алгебре квадратичная формула — это выражение в замкнутой форме, описывающее решения квадратного уравнения . Другие способы решения квадратных уравнений, например, заполнение квадрата , дают те же решения.

Учитывая общее квадратное уравнение вида $\textstyle ax^{2}+bx+c=0$, с $x$ представляющие неизвестное, и коэффициенты $a$, $b$, и $c$ представление известных действительных или комплексных чисел с помощью $a\neq 0$, значения $x$ удовлетворяющие уравнению, называемые корнями или нулями , можно найти с помощью квадратичной формулы,

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}},$$

где знак плюс-минус " $\pm$" указывает на то, что уравнение имеет два корня. Написанные отдельно, это:

$$x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}},\qquad x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}.$$

Количество $\textstyle \Delta =b^{2}-4ac$ называется дискриминантом квадратного уравнения. Если коэффициенты $a$, $b$, и $c$ действительные числа, тогда, когда $\Delta >0$, уравнение имеет два различных действительных корня; когда $\Delta =0$, уравнение имеет один повторяющийся вещественный корень; и когда $\Delta <0$, уравнение не имеет действительных корней, но имеет два различных комплексных корня, которые являются комплексно сопряженными друг другу.

Геометрически корни представляют собой $x$ значения, при которых график квадратичной функции $\textstyle y=ax^{2}+bx+c$, парабола , пересекает $x$-ось: график $x$-перехватывает. параболы Квадратную формулу также можно использовать для определения оси симметрии .

Вывод путем завершения квадрата

Чтобы завершить квадрат, сформируйте квадратный бином в левой части квадратного уравнения, из которого решение можно найти, извлекая квадратный корень из обеих частей.

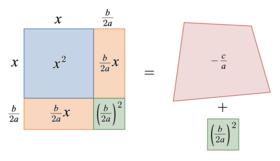
Стандартный способ вывода квадратной формулы — применить метод дополнения квадрата к общему квадратному уравнению. $\textstyle ax^{2}+bx+c=0$. Идея состоит в том, чтобы преобразовать уравнение в вид $\textstyle (x+k)^{2}=s$ для некоторых выражений $k$ и $s$записано через коэффициенты; извлеките квадратный корень из обеих частей; а затем изолировать $x$.

Начнем с деления уравнения на квадратичный коэффициент $a$, что разрешено, поскольку $a$не равно нулю. После этого вычитаем постоянный член $c/a$ чтобы изолировать его с правой стороны:

$${\begin{aligned}ax^{2{\vphantom {|}}}+bx+c&=0\\[3mu]x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}&=0\\[3mu]x^{2}+{\frac {b}{a}}x&=-{\frac {c}{a}}.\end{aligned}}$$

Левая часть теперь имеет вид $\textstyle x^{2}+2kx$, и мы можем «дополнить квадрат», добавив константу $\textstyle k^{2}$ чтобы получить квадрат бинома $\textstyle x^{2}+2kx+k^{2}={}$ $\textstyle (x+k)^{2}$. В этом примере мы добавляем $\textstyle (b/2a)^{2}$ в обе стороны, так что левую часть можно разложить на факторы:

$${\begin{aligned}x^{2}+2\left({\frac {b}{2a}}\right)x+\left({\frac {b}{2a}}\right)^{2}&=-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2}\\[5mu]\left(x+{\frac {b}{2a}}\right)^{2}&={\frac {b^{2}-4ac}{4a^{2}}}.\end{aligned}}$$

Поскольку левая часть теперь представляет собой идеальный квадрат, мы можем легко извлечь квадратный корень из обеих частей:

$$x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}.$$

Наконец, вычитая $b/2a$ с обеих сторон изолировать $x$ выводит квадратичную формулу:

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$$

Эквивалентные

Квадратную формулу можно эквивалентно записать с использованием различных альтернативных выражений, например

$$x=-{\frac {b}{2a}}\pm {\sqrt {\left({\frac {b}{2a}}\right)^{2}-{\frac {c}{a}}}},$$

которое можно получить, разделив квадратное уравнение на $2a$, в результате чего $\textstyle {\tfrac {1}{2}}x^{2}+{\tfrac {b}{2a}}x+{\tfrac {c}{2a}}=0$, затем подставляя новые коэффициенты в стандартную квадратичную формулу. Потому что этот вариант позволяет повторно использовать промежуточно рассчитанную величину ${\tfrac {b}{2a}}$, это может немного уменьшить используемую арифметику.

Квадратный корень в знаменателе

Менее известная квадратичная формула, впервые упомянутая Джулио Фаньяно : описывает те же корни через уравнение с квадратным корнем в знаменателе (при условии, что $c\neq 0$):

$$x={\frac {2c}{-b\mp {\sqrt {b^{2}-4ac}}}}.$$

Здесь знак минус–плюс » $\mp$" указывает на то, что два корня квадратного уравнения в том же порядке, что и стандартная квадратная формула, равны

$$x_{1}={\frac {2c}{-b-{\sqrt {b^{2}-4ac}}}},\qquad x_{2}={\frac {2c}{-b+{\sqrt {b^{2}-4ac}}}}.$$

Этот вариант в шутку назвали формулой «цитардаук» («квадратичная», написанная наоборот).

Когда $-b$ имеет противоположный знак как $\textstyle +{\sqrt {b^{2}-4ac}}$ или $\textstyle -{\sqrt {b^{2}-4ac}}$, вычитание может привести к катастрофической отмене , что приведет к низкой точности численных расчетов; выбор между вариантом квадратной формулы с квадратным корнем в числителе или знаменателе в зависимости от знака $b$можно избежать этой проблемы. См. § Численный расчет ниже.

Этот вариант квадратичной формулы используется в методе Мюллера для нахождения корней общих функций. Его можно получить по стандартной формуле из тождества $x_{1}x_{2}=c/a$, одна из формул Виеты . Альтернативно его можно получить путем деления исходного уравнения $\textstyle ax^{2}+bx+c=0$, к $\textstyle x^{2}$ получить $\textstyle cx^{-2}+bx^{-1}+a=0$, применяя стандартную формулу для нахождения двух корней $\textstyle x^{-1}\!$, а затем, взяв обратное значение, найти корни $x$ исходного уравнения.

Другие производные

Любой общий метод или алгоритм решения квадратных уравнений можно применить к уравнению с символьными коэффициентами и использовать для вывода некоторого выражения в замкнутой форме, эквивалентного квадратной формуле. Альтернативные методы иногда проще, чем заполнение квадрата, и могут предложить интересное понимание других областей математики.

Завершение квадрата по методу Шридхары

Вместо деления на $a$ изолировать $\textstyle x^{2}\!$, может быть немного проще умножить на $4a$ вместо этого производить $\textstyle (2ax)^{2}\!$, что позволяет нам заполнить квадрат без необходимости использования дробей. Тогда этапы вывода таковы:

1. Умножьте каждую сторону на $4a$.
2. Добавлять $\textstyle b^{2}-4ac$ в обе стороны, чтобы завершить квадрат.
3. Возьмите квадратный корень из обеих частей.
4. Изолировать $x$.

Применение этого метода к общему квадратному уравнению с символьными коэффициентами дает квадратную формулу:

$${\begin{aligned}ax^{2}+bx+c&=0\\[3mu]4a^{2}x^{2}+4abx+4ac&=0\\[3mu]4a^{2}x^{2}+4abx+b^{2}&=b^{2}-4ac\\[3mu](2ax+b)^{2}&=b^{2}-4ac\\[3mu]2ax+b&=\pm {\sqrt {b^{2}-4ac}}\\[5mu]x&={\dfrac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.{\vphantom {\bigg )}}\end{aligned}}$$

Этот метод завершения квадрата является древним и был известен индийскому математику VIII–IX веков Шридхаре . По сравнению с современным стандартным методом заполнения квадрата, этот альтернативный метод позволяет избежать дробей до последнего шага и, следовательно, не требует перестановки после шага 3 для получения общего знаменателя в правой части.

Путем замены

Другой вывод использует замену переменных, чтобы исключить линейный член. Тогда уравнение примет вид $\textstyle u^{2}=s$ с точки зрения новой переменной $u$ и некоторое постоянное выражение $s$, корни которого тогда $u=\pm {\sqrt {s}}$.

Подставив $x=u-{\tfrac {b}{2a}}$ в $\textstyle ax^{2}+bx+c=0$, расширяя продукты и объединяя подобные члены, а затем решая $\textstyle u^{2}\!$, у нас есть:

$${\begin{aligned}a\left(u-{\frac {b}{2a}}\right)^{2}+b\left(u-{\frac {b}{2a}}\right)+c&=0\\[5mu]a\left(u^{2}-{\frac {b}{a}}u+{\frac {b^{2}}{4a^{2}}}\right)+b\left(u-{\frac {b}{2a}}\right)+c&=0\\[5mu]au^{2}-bu+{\frac {b^{2}}{4a}}+bu-{\frac {b^{2}}{2a}}+c&=0\\[5mu]au^{2}+{\frac {4ac-b^{2}}{4a}}&=0\\[5mu]u^{2}&={\frac {b^{2}-4ac}{4a^{2}}}.\end{aligned}}$$

Наконец, после извлечения квадратного корня из обеих частей и подстановки полученного выражения на $u$ Вернуться в $x=u-{\tfrac {b}{2a}},$ выходит знакомая квадратичная формула:

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$$

Используя алгебраические тождества

Следующий метод использовался многими историческими математиками:

Пусть корни квадратного уравнения $\textstyle ax^{2}+bx+c=0$ быть $\alpha$ и $\beta$. Вывод начинается с тождества квадрата разности (действительного для любых двух комплексных чисел), из которого мы можем извлечь квадратный корень с обеих сторон:

$${\begin{aligned}(\alpha -\beta )^{2}&=(\alpha +\beta )^{2}-4\alpha \beta \\[3mu]\alpha -\beta &=\pm {\sqrt {(\alpha +\beta )^{2}-4\alpha \beta }}.\end{aligned}}$$

Поскольку коэффициент $a\neq 0$, мы можем разделить квадратное уравнение на $a$чтобы получить сводный многочлен с теми же корнями. А именно,

$$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=(x-\alpha )(x-\beta )=x^{2}-(\alpha +\beta )x+\alpha \beta .$$

Это означает, что сумма $\alpha +\beta =-{\tfrac {b}{a}}$ и продукт $\alpha \beta ={\tfrac {c}{a}}$. Таким образом, тождество можно переписать:

$$\alpha -\beta =\pm {\sqrt {\left(-{\frac {b}{a}}\right)^{2}-4{\frac {c}{a}}}}=\pm {\frac {\sqrt {b^{2}-4ac}}{a}}.$$

Поэтому,

$${\begin{aligned}\alpha &={\tfrac {1}{2}}(\alpha +\beta )+{\tfrac {1}{2}}(\alpha -\beta )=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac}}{2a}},\\[10mu]\beta &={\tfrac {1}{2}}(\alpha +\beta )-{\tfrac {1}{2}}(\alpha -\beta )=-{\frac {b}{2a}}\mp {\frac {\sqrt {b^{2}-4ac}}{2a}}.\end{aligned}}$$

Две возможности для каждого из $\alpha$ и $\beta$ — это одни и те же два корня в противоположном порядке, поэтому мы можем объединить их в стандартное квадратное уравнение:

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$$

По резольвентам Лагранжа

Дополнительная информация: резольвенты Лагранжа.

Альтернативный способ вывода квадратичной формулы — метод резольвент Лагранжа . это ранняя часть теории Галуа . Этот метод можно обобщить, чтобы получить корни кубических многочленов и многочленов четвертой степени , и приводит к теории Галуа, которая позволяет понимать решение алгебраических уравнений любой степени с точки зрения группы симметрии их корней, группы Галуа .

Этот подход фокусируется на самих корнях, а не на алгебраической перестановке исходного уравнения. Учитывая монический квадратичный полином $\textstyle x^{2}+px+q$ Предположим, что $\alpha$ и $\beta$это два корня. Таким образом, полиномиальные факторы как

$${\begin{aligned}x^{2}+px+q&=(x-\alpha )(x-\beta )\\[3mu]&=x^{2}-(\alpha +\beta )x+\alpha \beta \end{aligned}}$$

что подразумевает $p=-(\alpha +\beta )$ и $q=\alpha \beta$.

Поскольку умножение и сложение коммутативны , то замена корней $\alpha$ и $\beta$ не изменит коэффициенты $p$ и $q$: можно так сказать $p$ и $q$ являются симметричными полиномами от $\alpha$ и $\beta$. В частности, это элементарные симметричные многочлены – любой симметричный многочлен в $\alpha$ и $\beta$ может быть выражено через $\alpha +\beta$ и $\alpha \beta$ вместо.

Подход теории Галуа к анализу и решению многочленов состоит в том, чтобы задаться вопросом, можно ли с учетом коэффициентов многочлена, каждый из которых является симметричной функцией в корнях, «нарушить» симметрию и тем самым восстановить корни. Используя этот подход, решаем полином степени $n$ связано со способами перестановки (« перестановки ») $n$ терминах, называемых симметрической группой на $n$ буквы и обозначаются $S_{n}$. Для квадратичного многочлена единственный способ переставить два корня — это либо оставить их в покое, либо переставить их , поэтому решение квадратичного многочлена просто.

Чтобы найти корни $\alpha$ и $\beta$, рассмотрим их сумму и разность:

$$r_{1}=\alpha +\beta ,\quad r_{2}=\alpha -\beta .$$

Они называются резольвентами Лагранжа многочлена, из которых корни можно восстановить как

$$\alpha ={\tfrac {1}{2}}(r_{1}+r_{2}),\quad \beta ={\tfrac {1}{2}}(r_{1}-r_{2}).$$

Потому что $r_{1}=\alpha +\beta$ является симметричной функцией относительно $\alpha$ и $\beta$, это можно выразить через $p$ и $q,$ конкретно $r_{1}=-p$как описано выше. Однако, $r_{2}=\alpha -\beta$ не симметричен, так как поменяв местами $\alpha$ и $\beta$ дает аддитивную обратную $-r_{2}=\beta -\alpha$. Так $r_{2}$не может быть выражено через симметричные многочлены. Однако его площадь $\textstyle r_{2}^{2}=(\alpha -\beta )^{2}$ симметричен по корням, выражается через $p$ и $q$. Конкретно $\textstyle r_{2}^{2}=(\alpha -\beta )^{2}={}$ $\textstyle (\alpha +\beta )^{2}-4\alpha \beta ={}$ $\textstyle p^{2}-4q$, что подразумевает $\textstyle r_{2}=\pm {\sqrt {p^{2}-4q}}$. Взятие положительного корня «нарушает» симметрию, в результате чего

$$r_{1}=-p,\qquad r_{2}={\textstyle {\sqrt {p^{2}-4q}}}$$

откуда корни $\alpha$ и $\beta$ восстанавливаются как

$$x={\tfrac {1}{2}}(r_{1}\pm r_{2})={\tfrac {1}{2}}{\bigl (}{-p}\pm {\textstyle {\sqrt {p^{2}-4q}}}\,{\bigr )}$$

что является квадратичной формулой для монического многочлена.

Замена $p=b/a$, $q=c/a$дает обычное выражение для произвольного квадратичного многочлена. Резольвентами можно назвать

$${\tfrac {1}{2}}r_{1}=-{\tfrac {1}{2}}p=-{\frac {b}{2a}},\qquad r_{2}^{2}=p_{2}-4q={\frac {b^{2}-4ac}{a^{2}}},$$

соответственно вершина и дискриминант монического многочлена.

Похожий, но более сложный метод работает для кубических уравнений , которые имеют три резольвенты и квадратное уравнение («разрешающий полином»), связывающее $r_{2}$ и $r_{3}$, которое можно решить с помощью квадратного уравнения, и аналогично для уравнения четвертой степени ( степень 4), разрешающий полином которого является кубикой, которая, в свою очередь, может быть решена. Тот же метод для уравнения пятой степени дает полином 24-й степени, что не упрощает задачу, и фактически решения уравнений пятой степени вообще не могут быть выражены с использованием только корней.

Численный расчет

Квадратная формула абсолютно правильна, когда она выполняется с использованием идеализированной арифметики действительных чисел , но когда вместо нее используется приблизительная арифметика, например арифметика с ручкой и бумагой, выполняемая с фиксированным количеством десятичных знаков, или двоичная арифметика с плавающей запятой, доступная на компьютерах, ограничения представления чисел могут привести к существенно неточным результатам, если при реализации не будет уделено должного внимания. К особым трудностям относится катастрофическое сокращение при вычислении суммы $\textstyle -b\pm {\sqrt {\Delta }}$ если $\textstyle b\approx \pm {\sqrt {\Delta }}$; катастрофический расчет при вычислении дискриминанта $\textstyle \Delta =b^{2}-4ac$ себя в тех случаях, когда $\textstyle b^{2}\approx 4ac$; вырождение формулы, когда $a$, $b$, или $c$, представляется как ноль или бесконечность; и возможное переполнение или опустошение при умножении или делении очень больших или малых чисел, даже в тех случаях, когда корни могут быть точно представлены.

Катастрофическое сокращение происходит, когда вычитаются два числа, которые примерно равны. Хотя каждое из чисел может быть независимо представлено определенным количеством цифр точности, идентичные ведущие цифры каждого числа сокращаются, что приводит к разнице более низкой относительной точности. Когда $\textstyle b\approx {\sqrt {\Delta }}$, оценка $\textstyle -b+{\sqrt {\Delta }}$ вызывает катастрофическую отмену, как и оценка $\textstyle -b-{\sqrt {\Delta }}$ когда $\textstyle b\approx -{\sqrt {\Delta }}$. При использовании стандартной квадратичной формулы вычисление одного из двух корней всегда включает сложение, что сохраняет рабочую точность промежуточных вычислений, тогда как вычисление другого корня включает вычитание, что компрометирует его. Таким образом, наивное следование стандартной квадратичной формуле часто дает один результат с меньшей относительной точностью, чем ожидалось. К сожалению, вводные учебники по алгебре обычно не решают эту проблему, хотя из-за этого учащиеся получают неточные результаты по другим школьным предметам, таким как вводная химия.

Например, если попытаться решить уравнение $\textstyle x^{2}-1634x+2=0$ с помощью карманного калькулятора результат квадратной формулы $\textstyle x=817\pm {\sqrt {667\,487}}$ может быть приблизительно рассчитана как:

$${\begin{alignedat}{3}x_{1}&=817+816.998\,776\,0&&=1.633\,998\,776\times 10^{3},\\x_{2}&=817-816.998\,776\,0&&=1.224\times 10^{-3}.\end{alignedat}}$$

Несмотря на то, что калькулятор использовал десять десятичных цифр точности для каждого шага, вычисление разницы между двумя примерно равными числами дало результат $x_{2}$ всего четыре правильных цифры.

Одним из способов получения точного результата является использование идентификатора $x_{1}x_{2}=c/a$. В этом примере $x_{2}$ можно рассчитать как $x_{2}=2/x_{1}={}$ $1.223\,991\,125\times 10^{-3}\!$, что соответствует полным десяти цифрам. Другой более или менее эквивалентный подход — использовать версию квадратной формулы с квадратным корнем в знаменателе для вычисления одного из корней (см. § Квадратный корень в знаменателе выше).

Практические компьютерные реализации решения квадратных уравнений обычно выбирают, какую формулу использовать для каждого корня, в зависимости от знака уравнения. $b$.

Эти методы не предотвращают возможное переполнение или опустошение экспоненты с плавающей запятой при вычислении. $\textstyle b^{2}$ или $4ac$, что может привести к неточному вычислению численно представимых корней. Более надежная, но затратная в вычислительном отношении стратегия — начать с замены $\textstyle x=-u\operatorname {sgn}(b){\sqrt {\vert c\vert }}{\big /}\!{\sqrt {\vert a\vert }}$, превращая квадратное уравнение в

$$u^{2}-2{\frac {|b|}{2{\sqrt {|a|}}{\sqrt {|c|}}}}u+\operatorname {sgn}(c)=0,$$

где $\operatorname {sgn}$это знаковая функция . Сдача в аренду $\textstyle d=\vert b\vert {\big /}2{\sqrt {\vert a\vert }}{\sqrt {\vert c\vert }}$, это уравнение имеет вид $\textstyle u^{2}-2du\pm 1=0$, для которого одним решением является $\textstyle u_{1}=d+{\sqrt {d^{2}\mp 1}}$ и другое решение $\textstyle u_{2}=\pm 1/u_{1}$. Тогда корни исходного уравнения будут $\textstyle x_{1}=-\operatorname {sgn}(b){\bigl (}{\sqrt {\vert c\vert }}{\big /}\!{\sqrt {\vert a\vert }}~\!{\bigr )}u_{1}$ и $\textstyle x_{2}=-\operatorname {sgn}(b){\bigl (}{\sqrt {\vert c\vert }}{\big /}\!{\sqrt {\vert a\vert }}~\!{\bigr )}u_{2}$.

При дополнительном усложнении можно избежать затрат и дополнительного округления квадратных корней, аппроксимируя их степенями двойки, избегая при этом переполнения экспоненты для представимых корней.

Историческое развитие

Самые ранние методы решения квадратных уравнений были геометрическими. Вавилонские клинописные таблички содержат задачи, сводимые к решению квадратных уравнений. Египетский Берлинский папирус , относящийся к Среднему царству (2050–1650 гг. до н. э.), содержит решение двухчленного квадратного уравнения.

Греческий математик Евклид (около 300 г. до н.э.) использовал геометрические методы для решения квадратных уравнений во второй книге своих «Начал» , влиятельного математического трактата. Правила для квадратных уравнений появляются в китайской книге «Девять глав математического искусства» около 200 г. до н.э. В своей работе «Арифметика» греческий математик Диофант (около 250 г. н. э.) решал квадратные уравнения методом, более узнаваемым алгебраическим, чем геометрическая алгебра Евклида. Его решение дает только один корень, даже если оба корня положительны.

Индийский математик Брахмагупта включил общий метод поиска одного корня квадратного уравнения в свой трактат «Брахмаспхутасиддханта» (около 628 г. н. э.), написанный словами в стиле того времени, но более или менее эквивалентный современной символической формуле. Его решение квадратного уравнения $\textstyle ax^{2}+bx=c$ был следующим: «К абсолютному числу, умноженному на четырехкратный [коэффициент] квадрата, прибавьте квадрат [коэффициента] среднего члена; квадратный корень из того же числа за вычетом [коэффициента] среднего члена» , разделенный на двойной [коэффициент] квадрата, и есть значение». В современных обозначениях это можно записать $\textstyle x={\bigl (}{\sqrt {c\cdot 4a+b^{2}}}-b{\bigr )}{\big /}2a$. Индийский математик Шридхара (8–9 века) придумал аналогичный алгоритм решения квадратных уравнений в ныне утерянной работе по алгебре, цитируемой Бхаскарой II . Современную квадратичную формулу иногда называют формулой Шридхарачарьи . в Индии

Персидский математик 9-го века Мухаммад ибн Муса аль-Хорезми решал квадратные уравнения алгебраическим способом. Квадратичная формула, охватывающая все случаи, была впервые получена Саймоном Стевином в 1594 году. В 1637 году Рене Декарт опубликовал «Геометрию» , содержащую частные случаи квадратной формулы в той форме, которую мы знаем сегодня.

Геометрическое значение

С точки зрения координатной геометрии парабола, ориентированная по оси, представляет собой кривую, у которой $(x,y)$-координаты представляют собой график полинома второй степени вида $\textstyle y=ax^{2}+bx+c$, где $a$, $b$, и $c$ являются действительными постоянными коэффициентами с $a\neq 0$.

Геометрически квадратичная формула определяет точки $(x,0)$ на графике, где парабола пересекает $x$-ось. Кроме того, его можно разделить на два термина:

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}.$$

Первый член описывает ось симметрии , линию $x=-{\tfrac {b}{2a}}$. Второй срок, $\textstyle {\sqrt {b^{2}-4ac}}{\big /}2a$, дает расстояние, на котором корни находятся от оси симметрии.

Если вершина параболы лежит на $x$-ось, то соответствующее уравнение имеет единственный повторяющийся корень на линии симметрии, и этот член расстояния равен нулю; алгебраически дискриминант $\textstyle b^{2}-4ac=0$.

Если дискриминант положителен, то вершина не принадлежит $x$-ось, но парабола открывается в направлении $x$-ось, пересекая ее дважды, поэтому соответствующее уравнение имеет два действительных корня. Если дискриминант отрицательный, то парабола открывается в противоположном направлении, никогда не пересекая $x$-ось, и уравнение не имеет действительных корней; в этом случае два комплекснозначных корня будут комплексно-сопряженными , действительная часть которых равна $x$ значение оси симметрии.

Размерный анализ

Если константы $a$, $b$и/или $c$ не безразмерны , то величины $x$ и ${\tfrac {b}{a}}$ должны иметь одинаковые единицы измерения, поскольку условия $\textstyle ax^{2}$ и $bx$согласовать их единицы измерения. По той же логике коэффициент $c$ должны иметь те же единицы измерения, что и ${\tfrac {b^{2}}{a}}$, независимо от единиц измерения $x$. Это может быть мощным инструментом для проверки квадратичного выражения физических величин правильности настройки .

См. также

• Основная теорема алгебры
• Формулы Плейса

Ссылки

• Смит, Дэвид Юджин (1923), История математики , том. 2, Бостон: Джинн
• Ирвинг, Рон (2013), За пределами квадратичной формулы , MAA, ISBN  978-0-88385-783-0