Гомотетия

Гомотетия: пример с $k>0$
Для $k=1$ получается идентичность (ни одна точка не перемещается),
для $k>1$ расширение ​
для $k<1$ сокращение ​

Пример с $k<0$
Для $k=-1$ получается точечное отражение в точке $S$

Гомотетия пирамиды

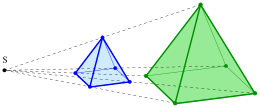
В математике гомотетия определяемого (или гомотеция , или однородное расширение ) — это преобразование аффинного пространства, точкой S, называемой ее центром , и ненулевым числом. $k$ называется его соотношением , которое отправляет точку $X$ в точку $X'$ по правилу

${\overrightarrow {SX'}}=k{\overrightarrow {SX}}$ за фиксированный номер $k\neq 0$.

Использование векторов положения:

$\mathbf {x} '=\mathbf {s} +k(\mathbf {x} -\mathbf {s} )$.

В случае $S=O$ (Источник):

$\mathbf {x} '=k\mathbf {x}$,

который представляет собой равномерное масштабирование и показывает значение специального выбора для $k$:

для $k=1$ мы получаем сопоставление идентичности ,

для $k=-1$ получается отражение в центре,

Для $1/k$ получается обратное отображение, определенное формулой $k$.

В евклидовой геометрии гомотетиями называют подобия , которые фиксируют точку и либо сохраняют (если $k>0$) или наоборот (если $k<0$) направление всех векторов. Вместе с трансляциями все гомотетии аффинного (или евклидова) пространства образуют группу — группу дилатаций или гомотетий-трансляций . Это именно аффинные преобразования , обладающие тем свойством, что образ каждой прямой g является линией параллельной g , .

В проективной геометрии гомотетическое преобразование — это преобразование подобия (т. е. фиксирует заданную эллиптическую инволюцию), которое оставляет линию на бесконечности поточечно инвариантной .

В евклидовой геометрии гомотетия отношения $k$ умножает расстояния между точками на $|k|$, площади по $k^{2}$ и объемы по $|k|^{3}$. Здесь $k$ это коэффициент увеличения или коэффициент расширения , или масштабный коэффициент , или коэффициент подобия . Такое преобразование можно назвать расширением, если масштабный коэффициент превышает 1. Упомянутая выше неподвижная точка S называется центром подобия , центром подобия или центром подобия .

Термин, придуманный французским математиком Мишелем Шалем , происходит от двух греческих элементов: префикса гомо- ( όμο ), означающего «подобный», и тезиса ( Θέσις ), означающего «положение». Он описывает отношения между двумя фигурами одинаковой формы и ориентации. Например, две русские куклы, смотрящие в одну сторону, можно считать гомотетичными.

Гомотетии используются для масштабирования содержимого экранов компьютеров; например, смартфоны, ноутбуки и ноутбуки.

Характеристики

Следующие свойства сохраняются в любом измерении.

Отображение линий, сегментов линий и углов

Гомотетия обладает следующими свойствами:

• Линия . отображается на параллельную линию Следовательно: углы остаются неизменными.
• Соотношение двух отрезков сохраняется.

Оба свойства показывают:

• Гомотетия – это сходство .

Вывод свойств: Для упрощения расчетов предполагается, что центр $S$ это происхождение: $\mathbf {x} \to k\mathbf {x}$. линия $g$ с параметрическим представлением $\mathbf {x} =\mathbf {p} +t\mathbf {v}$ отображается на набор точек $g'$ с уравнением $\mathbf {x} =k(\mathbf {p} +t\mathbf {v} )=k\mathbf {p} +tk\mathbf {v}$, которая представляет собой линию, параллельную $g$.

Расстояние в две точки $P:\mathbf {p} ,\;Q:\mathbf {q}$ является $|\mathbf {p} -\mathbf {q} |$ и $|k\mathbf {p} -k\mathbf {q} |=|k||\mathbf {p} -\mathbf {q} |$ расстояние между их изображениями. Следовательно, соотношение (частное) двух отрезков остается неизменным.

В случае $S\neq O$ расчет аналогичен, но немного расширен.

Последствия: Треугольник отображается на подобный . Однородным образом круга является круг. Изображение эллипса аналогично . т.е. соотношение двух осей не меняется.

С теоремой о перехвате

Графические конструкции

используя теорему о пересечении

Если для гомотетии с центром $S$ изображение $Q_{1}$ точки $P_{1}$ задано (см. схему), то изображение $Q_{2}$ второго пункта $P_{2}$, который лежит не на линии $SP_{1}$ можно построить графически с помощью теоремы о пересечении: $Q_{2}$ это общая точка двух линий ${\overline {P_{1}P_{2}}}$ и ${\overline {SP_{2}}}$. Изображение точки, коллинеарное $P_{1},Q_{1}$ можно определить с помощью $P_{2},Q_{2}$.

Пантограф

Геометрический фон

Пантограф 3d рендеринг

с помощью пантографа

До того, как компьютеры стали повсеместными, масштабирование рисунков выполнялось с помощью пантографа — инструмента, похожего на компас .

Строительная и геометрическая основа:

1. Возьмите 4 стержня и соберите подвижный параллелограмм с вершинами. $P_{0},Q_{0},H,P$ так, что два стержня встречаются в $Q_{0}$ удлинены на другом конце, как показано на рисунке. Выберите соотношение $k$.
2. На удлиненных стержнях отметьте две точки. $S,Q$ такой, что $|SQ_{0}|=k|SP_{0}|$ и $|QQ_{0}|=k|HQ_{0}|$. Это тот случай, если $|SQ_{0}|={\tfrac {k}{k-1}}|P_{0}Q_{0}|.$ (Вместо $k$ расположение центра $S$ можно прописать. В этом случае соотношение $k=|SQ_{0}|/|SP_{0}|$.)
3. Прикрепите подвижные стержни с возможностью вращения в точке $S$.
4. Меняйте расположение точки $P$ и отмечайте в каждый момент времени $Q$.

Из-за $|SQ_{0}|/|SP_{0}|=|Q_{0}Q|/|PP_{0}|$ получается (см. диаграмму) из теоремы о пересечении , что точки $S,P,Q$ коллинеарны (лежат на прямой) и уравнение $|SQ|=k|SP|$ держит. Это показывает: отображение $P\to Q$ является гомотетией с центром $S$ и соотношение $k$.

Состав

Композиция двух гомотетий с центрами $S_{1},S_{2}$ и соотношения $k_{1}=2,k_{2}=0{.}3$ картографирование $P_{i}\to Q_{i}\to R_{i}$ снова является гомотетией со своим центром $S_{3}$ онлайн ${\overline {S_{1}S_{2}}}$ с соотношением $k\cdot l=0{.}6$.

• Состав двух гомотетий с одним и тем же центром $S$ снова гомотетия с центром $S$. Гомотетии с центром $S$ сформировать группу .
• Состав двух гомотетий с разными центрами $S_{1},S_{2}$ и его соотношения $k_{1},k_{2}$ является

в случае $k_{1}k_{2}\neq 1$ гомотетия с центром на линии ${\overline {S_{1}S_{2}}}$ и соотношение $k_{1}k_{2}$ или

в случае $k_{1}k_{2}=1$ перевод направлении в ${\overrightarrow {S_{1}S_{2}}}$. Особенно, если $k_{1}=k_{2}=-1$ ( точечные отражения ).

Вывод:

Для композиции $\sigma _{2}\sigma _{1}$ из двух гомотетий $\sigma _{1},\sigma _{2}$ с центрами $S_{1},S_{2}$ с

$\sigma _{1}:\mathbf {x} \to \mathbf {s} _{1}+k_{1}(\mathbf {x} -\mathbf {s} _{1}),$

$\sigma _{2}:\mathbf {x} \to \mathbf {s} _{2}+k_{2}(\mathbf {x} -\mathbf {s} _{2})\$

получается расчетным путем для изображения точки $X:\mathbf {x}$:

$(\sigma _{2}\sigma _{1})(\mathbf {x} )=\mathbf {s} _{2}+k_{2}{\big (}\mathbf {s} _{1}+k_{1}(\mathbf {x} -\mathbf {s} _{1})-\mathbf {s} _{2}{\big )}$

$\qquad \qquad \ =(1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}+k_{1}k_{2}\mathbf {x}$.

Следовательно, композиция

в случае $k_{1}k_{2}=1$ перевод в направлении ${\overrightarrow {S_{1}S_{2}}}$ по вектору $\ (1-k_{2})(\mathbf {s} _{2}-\mathbf {s} _{1})$.

в случае $k_{1}k_{2}\neq 1$ точка

$S_{3}:\mathbf {s} _{3}={\frac {(1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}}{1-k_{1}k_{2}}}=\mathbf {s} _{1}+{\frac {1-k_{2}}{1-k_{1}k_{2}}}(\mathbf {s} _{2}-\mathbf {s} _{1})$

является фиксированной точкой (не перемещается) и композиция

$\sigma _{2}\sigma _{1}:\ \mathbf {x} \to \mathbf {s} _{3}+k_{1}k_{2}(\mathbf {x} -\mathbf {s} _{3})\quad$.

является гомотетией с центром $S_{3}$ и соотношение $k_{1}k_{2}$. $S_{3}$ лежит на линии ${\overline {S_{1}S_{2}}}$.

Сочинение с переводом

• Соединение гомотети и перевода есть гомотетия.

Вывод:

Состав гомотетии

$\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} ),\;k\neq 1,\;$ и перевод

$\tau :\mathbf {x} \to \mathbf {x} +\mathbf {v}$ является

$\tau \sigma :\mathbf {x} \to \mathbf {s} +\mathbf {v} +k(\mathbf {x} -\mathbf {s} )$

$=\mathbf {s} +{\frac {\mathbf {v} }{1-k}}+k\left(\mathbf {x} -(\mathbf {s} +{\frac {\mathbf {v} }{1-k}})\right)$

что является гомотетией с центром $\mathbf {s} '=\mathbf {s} +{\frac {\mathbf {v} }{1-k}}$ и соотношение $k$.

В однородных координатах

Гомотетия $\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} )$ с центром $S=(u,v)$ можно записать как композицию гомотети с центром $O$ и перевод:

$\mathbf {x} \to k\mathbf {x} +(1-k)\mathbf {s}$.

Следовательно $\sigma$ можно представить в однородных координатах по матрице:

${\begin{pmatrix}k&0&(1-k)u\\0&k&(1-k)v\\0&0&1\end{pmatrix}}$

чистой гомотетии Линейное преобразование также является конформным , поскольку оно состоит из трансляции и равномерного масштаба.

См. также

• Масштабирование (геометрия) - аналогичное понятие в векторных пространствах.
• Гомотетический центр , центр гомотетического преобразования, переводящего одну из пары фигур в другую.
• о Гипотеза Хадвигера количестве строго меньших гомотетических копий выпуклого тела, которые могут понадобиться для его покрытия.
• Гомотетическая функция (экономика) — функция вида f ( U ( y )), в которой U — однородная функция , а f — монотонно возрастающая функция .

Ссылки

• HSM Coxeter, «Введение в геометрию», Wiley (1961), с. 94
• Адамар Ж. Уроки плоской геометрии.
• Месерв, Брюс Э. (1955), «Гомотетические преобразования», «Фундаментальные концепции геометрии» , Аддисон-Уэсли , стр. 166–169.
• Туллер, Аннита (1967), Современное введение в геометрию , Университетская серия по математике для студентов, Принстон, Нью-Джерси: D. Van Nostand Co.

Внешние ссылки

• Homothety , интерактивный апплет от Cut-the-Knot .