Фундаментальный многоугольник
В математике можно фундаментальный многоугольник определить для каждой компактной римановой поверхности рода больше 0. Он кодирует не только топологию поверхности через ее фундаментальную группу , но также определяет риманову поверхность с точностью до конформной эквивалентности. По теореме об униформизации каждая компактная риманова поверхность имеет односвязную универсальную накрывающую поверхность, заданную ровно одним из следующих:
В первом случае нулевого рода поверхность конформно эквивалентна сфере Римана.
Во втором случае рода один поверхность конформно эквивалентна тору C /Λ для некоторой решетки Λ в C . Фундаментальный многоугольник Λ, если предположить, что он выпуклый, может быть либо параллелограммом периода, либо центрально-симметричным шестиугольником - результат, впервые доказанный Федоровым в 1891 году.
В последнем случае рода g > 1 риманова поверхность конформно эквивалентна H /Γ, где Γ — фуксова группа преобразований Мёбиуса . Фундаментальная область для Γ задается выпуклым многоугольником для гиперболической метрики на H . Они могут быть определены многоугольниками Дирихле и иметь четное количество сторон. По такому многоугольнику можно прочитать структуру фундаментальной группы Γ. Используя теорию квазиконформных отображений и уравнение Бельтрами , можно показать, что существует канонический выпуклый фундаментальный многоугольник с 4 g сторонами, впервые определенный Фрике , который соответствует стандартному представлению Γ как группы с 2 g образующими a 1 , b 1 , a 2 , b 2 , ..., a g , b g и единственное соотношение [ a 1 , b 1 ][ a 2 , b 2 ] ⋅⋅⋅ [ a g , b g ] = 1, где [ а , б ] знак равно а б а −1 б −1 .
Любая риманова метрика на ориентированном замкнутом 2-многообразии M определяет комплексную структуру на M , что делает M компактной римановой поверхностью. Из использования фундаментальных многоугольников следует, что два ориентированных замкнутых 2-многообразия классифицируются по их роду, то есть половине ранга абелевой группы Γ/[Γ, Γ], где Γ = π 1 ( M ). Более того, из теории квазиконформных отображений следует также, что две компактные римановы поверхности диффеоморфны тогда и только тогда, когда они гомеоморфны. Следовательно, два замкнутых ориентированных 2-многообразия гомеоморфны тогда и только тогда, когда они диффеоморфны. Такой результат можно доказать и методами дифференциальной топологии . [1] [2]
первого рода многоугольники Фундаментальные


Параллелограммы и центрально - симметричные шестиугольники
В случае рода один фундаментальный выпуклый многоугольник ищется для действия переносом Λ = Z a ⊕ Z b на R 2 = C где a и b линейно независимы над R. , (После выполнения реального линейного преобразования на R 2 , при необходимости можно считать, что Λ = Z 2 знак равно Z + Z я ; для римановой поверхности рода один ее можно принять в виде Λ = Z 2 = Z + Z ω, причем Im ω > 0.) Фундаментальная область задается параллелограммом s x + t y для 0 < s , t < 1 , где x и y — образующие Λ.
Если C — внутренняя часть фундаментального выпуклого многоугольника, то сдвиги C + x покрывают R 2 поскольку x пробегает Λ. Отсюда следует, что граничные точки C образуются пересечениями C ∩ ( C + x ). Это выпуклые компакты в ∂ C и, следовательно, либо вершины C , либо стороны C . Отсюда следует, что каждую замкнутую сторону C можно записать таким образом. Если перевести на − x , то C ∩ ( C − x ) также является стороной C . Таким образом, стороны C встречаются в параллельных парах одинаковой длины. Конечные точки двух таких параллельных отрезков одинаковой длины можно соединить так, что они пересекаются и пересечение происходит в середине отрезков, соединяющих конечные точки. Отсюда следует, что пересечения всех таких отрезков происходят в одной и той же точке. Переведя эту точку в начало координат, следует, что многоугольник центрально симметричен; то есть, если точка z находится в многоугольнике, то и − z тоже .
Легко увидеть, как центрально-симметричный выпуклый шестиугольник замощает плоскость. Если A — точка шестиугольника, то решетка порождается векторами смещения AB и AC где B и C — две вершины, которые не являются соседями A и не противолежат A. , Действительно, на второй картинке показано, насколько шестиугольник эквивалентен параллелограмму, полученному смещением двух отрубленных треугольников отрезками AB и AC . Столь же хорошо на первой картинке показан другой способ сопоставления мозаики параллелограммами с шестиугольной мозаикой. Если центр шестиугольника равен 0, а вершины по порядку — a , b , c , − a , — b и — c , то Λ — абелева группа с образующими a + b и b + c .
фундаментальных многоугольников, созданных с параллелограммов помощью Примеры
Существует ровно четыре топологии, которые можно создать, определив стороны ромба разными способами. Они приведены ниже в виде направленных ребер A и B на квадрате в виде последовательностей AABB или ABAB.
| Имя | Сфера | Тор | Проекционная плоскость | бутылка Клейна |
|---|---|---|---|---|
| Регулируемый | Да | Нет | ||
| Полная кривизна | 4р | 0 | 2 р | 0 |
| Топология АБАБ (квадрат) | 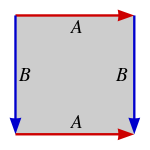 |  |  (или ) | |
| Топология ААББ (квадрат) | 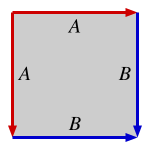 [3] |  (или ) |  | |
| Геометрия |  Сфера |  Тор |  полушарие |  Полутор |
Теорема Федорова [ править ]
Теорема Федорова , установленная русским кристаллографом Евграфом Федоровым в 1891 году, утверждает, что параллелограммы и центрально-симметричные шестиугольники — единственные выпуклые многоугольники, которые являются фундаментальными областями. [4] Есть несколько доказательств этого, некоторые из самых последних связаны с результатами в теории выпуклости , геометрии чисел и упаковке кругов , такими как неравенство Брунна-Минковского . [5] два элементарных доказательства, принадлежащих Х.С.М. Кокстеру и Вороному . Здесь будут представлены [6] [7]
Доказательство Коксетера продолжается в предположении, что существует центрально-симметричный выпуклый многоугольник C с 2 m сторонами. Тогда большой замкнутый параллелограмм образовался из N 2 Фундаментальный параллелограмм состоит из сдвигов буквы C , выходящих за края большого параллелограмма. Это индуцирует замощение на торе C / N Λ. Пусть v , e и f — количество вершин, ребер и граней в этом разбиении (с учетом отождествлений в факторпространстве). Тогда, поскольку характеристика Эйлера–Пуанкаре тора равна нулю,
С другой стороны, поскольку каждая вершина находится как минимум на трех разных ребрах и каждое ребро находится между двумя вершинами,
Более того, поскольку каждое ребро принадлежит ровно двум граням,
Следовательно
так что
по мере необходимости.
Доказательство Вороного начинается с наблюдения, что каждое ребро C соответствует элементу x из Λ. Фактически ребро — это ортогональная биссектриса радиуса от 0 до x . Следовательно, основание перпендикуляра, проведенного из точки 0 к каждому ребру, лежит внутри каждого ребра. Если y — любая точка решетки, то 1/2 y не может лежать в C ; в этом случае –1/2 y также будет лежать в C , что противоречит тому, что C является фундаментальной областью для Λ. Пусть ± x 1 , ..., ± x m — 2 m различных точек Λ, соответствующих сторонам C . Зафиксируем образующие a и b группы Λ. Таким образом, x i = α i a + β i b , где α i и β i — целые числа. Невозможно, чтобы оба α i и β i были четными, поскольку в противном случае ± 1/2 x i была бы точкой Λ на стороне, что противоречит тому, что C является фундаментальной областью. Таким образом, существует три возможности для пары целых чисел (α i , β i ) по модулю 2: (0,1), (1,0) и (1,1). Следовательно, если m > 3, будут x i и x j с i ≠ j , причем обе координаты x i − x j четны, т.е. 1/2 ( x i + x j ) лежит в Λ. Но это середина отрезка, соединяющего две внутренние точки ребер, и, следовательно, лежит в C — внутренняя часть многоугольника. Это снова противоречит тому факту, что C является фундаментальной областью. Итак, доведение до абсурда m ≤ 3, как утверждается.
Домены Дирихле – Вороного [ править ]
Для решетки Λ в C = R 2 фундаментальная область может быть определена канонически с использованием конформной структуры C . Обратите внимание, что группа конформных преобразований C задается комплексными аффинными преобразованиями g ( z ) = az + b с a ≠ 0 . Эти преобразования сохраняют евклидову метрику d ( z , w ) = | г - ш | с точностью до множителя, а также сохраняя ориентацию . Это подгруппа группы Мёбиуса, фиксирующая точку ∞. Метрическую структуру можно использовать для определения канонической фундаментальной области по формуле C = { z : d ( z , 0) < d ( z , λ ) для всех λ ≠ 0 в Λ}. (Из определения очевидно, что это фундаментальная область.) Это пример области Дирихле или диаграммы Вороного : поскольку комплексные сдвиги образуют абелеву группу, поэтому коммутируют с действием Λ, эти понятия совпадают. Каноническая фундаментальная область для Λ = Z + Z ω с Im ω > 0 представляет собой либо симметричный выпуклый параллелограмм, либо шестиугольник с центром 0. По конформной эквивалентности период ω может быть дополнительно ограничен для удовлетворения | Ре ω | ≤ 1/2 и | ω | ≥ 1 . Как показал Дирихле («Теорема Дирихле о шестиугольнике», 1850), почти для всех ω фундаментальная область представляет собой шестиугольник. При Re ω > 0 середины сторон определяются как ±1/2, ± ω /2 и ±( ω – 1)/2 ; стороны делят пополам соответствующие радиусы от 0 ортогонально, что полностью определяет вершины. Фактически первая вершина должна иметь вид (1 + ix )/2 и ω (1 + iy )/2 с действительными x и y ; поэтому, если ω = a + ib , то a – by = 1 и x = b + ay . Следовательно, y = ( a – 1)/ b и x = ( a 2 + б 2 – а )/ б . Таким образом, шесть вершин — это ± ω (1 – iy )/2 и ±(1 ± ix )/2 . [8]
высшего рода многоугольники Фундаментальные
Обзор [ править ]
Каждая компактная риманова поверхность X имеет универсальную накрывающую поверхность которая является односвязной римановой поверхностью X. , Фундаментальная группа X может быть отождествлена с подгруппой Γ как преобразования колоды и X группы биголоморфизмов X действует . Таким образом, группа Γ действует свободно на X с компактным фактор-пространством X /Γ, которое можно отождествить с X . Таким образом, классификацию компактных римановых поверхностей можно свести к изучению возможных групп Γ. По теореме об униформизации X представляет собой либо сферу Римана, комплексную плоскость, либо единичный диск/верхнюю полуплоскость. Первым важным инвариантом компактной римановой поверхности является ее род , топологический инвариант, заданный половиной ранга абелевой группы Γ/[Γ, Γ] (которая может быть отождествлена с группой гомологий H 1 ( X , Z ) ). Род равен нулю, если накрывающим пространством является сфера Римана; один, если это комплексная плоскость; и больше единицы, если это единичный диск или верхняя полуплоскость. [9]
Бигомоломорфизмы сферы Римана представляют собой просто комплексные преобразования Мёбиуса, и каждое нетождественное преобразование имеет хотя бы одну неподвижную точку, поскольку соответствующая комплексная матрица всегда имеет хотя бы один ненулевой собственный вектор. Таким образом, если X — сфера Римана, то X должно быть односвязным и биголоморфным сфере Римана — римановой поверхности нулевого рода . Когда X — комплексная плоскость, группа биголоморфизмов — это аффинная группа, комплексные преобразования Мёбиуса фиксируют ∞, поэтому преобразования g ( z ) = az + b с a ≠ 0 . Нетождественные преобразования без неподвижных точек — это преобразования с a = 1 и b ≠ 0 , то есть ненулевые сдвиги. Таким образом, группу Γ можно отождествить с решеткой Λ в C и X с фактором C /Λ, как описано в разделе о фундаментальных многоугольниках первого рода. В третьем случае, когда X — единичный круг или верхняя полуплоскость, группа биголоморфизмов состоит из комплексных преобразований Мёбиуса, фиксирующих единичную окружность или вещественную ось. В первом случае преобразования соответствуют элементам группы SU(1, 1)/{± I }; в последнем случае они соответствуют вещественным преобразованиям Мёбиуса, то есть элементам SL(2, R )/{± I }. [9]
Изучение и классификация возможных групп Γ, свободно действующих на единичном круге или верхней полуплоскости с компактным фактором, — фуксовых групп первого рода — может быть осуществлена путем изучения их фундаментальных многоугольников, как описано ниже. Как заметил Пуанкаре , каждый такой многоугольник обладает особыми свойствами, а именно: он выпуклый и имеет естественное спаривание между сторонами. Они не только позволяют восстановить группу, но и обеспечивают явное представление группы с помощью генераторов и отношений. И наоборот, Пуанкаре доказал, что любой такой многоугольник порождает компактную риманову поверхность; Фактически, теорема Пуанкаре о многоугольниках применялась к более общим многоугольникам, где многоугольнику разрешалось иметь идеальные вершины, но его доказательство было полным только в компактном случае, без таких вершин. Без предположений о выпуклости многоугольника полные доказательства были даны Маскитом и де Рамом , основанные на идее Сигела , и их можно найти в Beardon (1983) , Iversen (1992) и Stillwell (1992) . Каратеодори дал элементарную трактовку существования мозаик треугольниками Шварца , т.е. мозаик геодезическими треугольниками с углами π / a , π / b , π / c с суммой меньше π , где a , b , c — целые числа. Когда все углы равны π /2 g , это устанавливает замощение правильными 4g- сторонними гиперболическими многоугольниками и, следовательно, существование конкретной компактной римановой поверхности рода g как фактор-пространства. Этот специальный пример, имеющий циклическую группу Z 2 g бигомоломорфных симметрий, используется в дальнейшем развитии. [9]
Классификация с точностью до гомеоморфизма и диффеоморфизма компактных римановых поверхностей влечет за собой классификацию замкнутых ориентируемых 2-многообразий с точностью до гомеоморфизма и диффеоморфизма: любые два 2-многообразия одного и того же рода диффеоморфны. Фактически, используя разбиение единицы, каждое замкнутое ориентируемое 2-многообразие допускает риманову метрику . Для компактной римановой поверхности можно ввести также конформную метрику, которая является конформной, так что в голоморфных координатах метрика принимает вид ρ ( z ) | дз | 2 . После выбора этой метрики локально биголоморфные отображения представляют собой в точности сохраняющие ориентацию диффеоморфизмы, которые являются конформными, т. е. масштабируют метрику с помощью гладкой функции. Существование изотермических координат , которое можно доказать с помощью либо локальных теорем существования для лапласиана , либо уравнения Бельтрами , показывает, что каждому замкнутому ориентированному риманову 2-многообразию может быть придана комплексная структура, совместимая с его метрикой, и, следовательно, оно имеет структуру компактная риманова поверхность. Эта конструкция показывает, что классификацию замкнутых ориентируемых 2-многообразий с точностью до диффеоморфизма или гомеоморфизма можно свести к случаю компактных римановых поверхностей. [10]
Классификацию компактных римановых поверхностей с точностью до гомеоморфизма и диффеоморфизма можно осуществить с помощью фундаментального многоугольника. Действительно, как заметил Пуанкаре, выпуклые фундаментальные многоугольники для компактных римановых поверхностей H /Γ могут быть построены путем адаптации метода Дирихле из евклидова пространства к гиперболическому пространству. Затем, следуя Неванлинне и Йосту, фундаментальную область можно поэтапно изменить, чтобы получить невыпуклый многоугольник с вершинами, лежащими на одной орбите Γ, и кусочно-геодезическими сторонами. На каждом из этих шагов также модифицируется соотношение пар на сторонах. Каждый шаг включает разрезание многоугольника диагональным геодезическим сегментом внутри многоугольника и повторную сборку многоугольника с использованием одного из преобразований Мёбиуса, участвующих в спаривании. Никакие две парные стороны не могут иметь общую вершину в конечном парном отношении, которое удовлетворяет свойствам, аналогичным свойствам исходного отношения. Этот многоугольник, в свою очередь, можно последовательно модифицировать, собирая его заново после разрезания его диагональным кусочно-геодезическим сегментом внутри него. Последний многоугольник имеет 4 g эквивалентных вершин со сторонами, кусочно геодезическими. Стороны помечены элементами группы, которые дают преобразование Мёбиуса парной стороне. Чтобы маркировка была
так что Γ порождается a i и b i, подчиняющимися единственному соотношению
- Род нулевая поверхность (сфера)
- Род первая поверхность (тор)
- Род второй поверхность
- Род третий поверхность
Используя теорию чисел пересечений , следует, что форма, полученная путем соединения вершин геодезическими, также является правильным многоугольником, не обязательно выпуклым, а также является фундаментальной областью с теми же элементами группы, дающими спаривание. В результате получается фундаментальный многоугольник с краями, заданными геодезическими сегментами, и со стандартной маркировкой. Абелианизация Γ, факторгруппа Γ/[Γ, Γ] , является свободной абелевой группой с 2 g образующими. Таким образом, род g является топологическим инвариантом. Легко видеть, что две римановы поверхности одного и того же рода гомеоморфны, поскольку являются топологическим пространством, поскольку они получаются отождествлением сторон 4 g -стороннего многоугольника — евклидова многоугольника в модели Клейна — посредством диффеоморфизмов между парными сторонами. [11] Применение этой конструкции к правильному 4 - стороннему многоугольнику позволяет топологически рассматривать риманову поверхность как пончик с g- дырками - стандартное описание ориентированных поверхностей во вводных текстах по топологии. [12] [13]
Есть еще несколько результатов:
- Две гомеоморфные римановы поверхности диффеоморфны.
- Любой выпуклый фундаментальный многоугольник рода g имеет N вершин, где 4 g ≤ N ≤ 12 g – 6.
- Многоугольник Дирихле рода g имеет ровно 12 g – 6 вершин для плотного открытого множества центров.
- Каждая риманова поверхность рода g имеет фундаментальный многоугольник Фрике, т. е. выпуклый многоугольник с каноническим спариванием сторон. (Многоугольник не обязательно должен быть многоугольником Дирихле.)
- После подходящей нормализации и маркировки генераторов фундаментальной группы многоугольник Фрике определяется однозначно, и 6 g – 6 действительных параметров, описывающих его, могут использоваться в качестве глобальных вещественных аналитических параметров для пространства Тейхмюллера в роде g .
Эти результаты связаны с взаимосвязью гомеоморфизмов и фундаментальной группы: это отражает тот факт, что группа классов отображений римановой поверхности — группа квазиконформных самомоморфизмов римановой поверхности H /Γ по модулю гомотопных тождеству — можно отождествить с внешней группой автоморфизмов группы Γ ( теорема Дена–Нильсена–Бэра ). [14] Чтобы увидеть эту связь, заметим, что если f — квазиконформный гомеоморфизм X 1 = H /Γ 1 на X 2 = H / 2 , то f поднимается до квазиконформного гомеоморфизма f группы H на себя. Этот подъем уникален с точностью до прекомпозиции с элементами Γ 1 и посткомпозиции с элементами Γ 2 . Если π i — проекция H на X i , то f ∘ π 1 = π 2 ∘ f и Γ i — это просто группа гомеоморфизмов g группы H таких, что π i ∘ g = π i . Отсюда следует, что f g = θ ( g ) f для g в Γ 1 , где θ — групповой изоморфизм Γ 1 на Γ 2 . Другой выбор f меняет θ путем композиции с внутренним автоморфизмом: такие изоморфизмы называются эквивалентными . [15]
Два изоморфизма θ и θ ′ эквивалентны тогда и только тогда, когда соответствующие гомеоморфизмы f и f ′ гомотопны. Фактически достаточно показать, что квазиконформный самогомеоморфизм f поверхности индуцирует внутренний автоморфизм фундаментальной группы тогда и только тогда, когда он гомотопен тождественному отображению: другими словами, гомоморфизм квазиконформной группы самогомеоморфизмов H /Γ в Out Γ переходит в группу классов отображений, на которой он инъективен. Действительно, предположим сначала, что F ( t ) — непрерывный путь самогомеоморфизмов с F (0) = id и F (1) = f . Тогда существует непрерывный лифт F ( t ) с F (0) = id. Более того, для каждого g в Γ F ( t ) ∘ g ∘ F ( t ) −1 — непрерывно меняющийся элемент Γ, равный g при t = 0 ; поэтому дискретность Γ заставляет этот элемент быть постоянным и, следовательно, равным g, так что F ( t ) коммутирует с Γ, поэтому F (1) индуцирует тривиальный автоморфизм. Если, с другой стороны, F — квазиконформный лифт f, индуцирующий внутренний автоморфизм Γ, то после композиции с элементом Γ, если необходимо, можно предположить, что F коммутирует с Γ. Поскольку F квазиконформен, он продолжается до квазисимметричного гомеоморфизма окружности, который также коммутирует с Γ. Каждый g ≠ id в Γ является гиперболическим, поэтому имеет две неподвижные точки на окружности a ± такие, что для всех остальных точек z , g ± n ( z ) стремится к a ±, поскольку n стремится к бесконечности. Следовательно, F должен зафиксировать эти точки; поскольку эти точки плотны в круге при изменении g , отсюда следует, что F фиксирует единичный круг. Пусть µ = F z / F z , так что µ является Γ-инвариантным дифференциалом Бельтрами. Пусть F ( t ) — решение уравнения Бельтрами tμ, нормализованное для фиксации трех точек на единичной окружности. Тогда F ( t ) коммутирует с Γ и, следовательно, как и F = F (1) , является единицей на единичной окружности. По построению F ( t ) является изотопией единицы F. и Это доказывает инъективность. [15]
Доказательство сюръективности основано на сравнении гиперболической метрики на D с метрикой длины слова на Γ. [16] Если предположить, не ограничивая общности, что 0 лежит внутри выпуклого фундаментального многоугольника C , а g является элементом Γ, луч от 0 до g (0) — гиперболическая геодезическая — проходит через последовательность сдвигов C . Каждый из них получается из предыдущего применением генератора Γ или фиксированного произведения генераторов (если в вершине встречаются последовательные сдвиги). Отсюда следует, что гиперболическое расстояние между 0 и g (0) меньше, чем 4 g , умноженное на длину слова g плюс двойной диаметр основного многоугольника. Таким образом, метрика на Γ d 1 ( g , h ) = L ( h −1 g ), определяемый длиной слова L ( g ), удовлетворяет
для положительных констант a и b . Обратно, существуют положительные константы c и d такие, что
Многоугольники Дирихле [ править ]
Учитывая точку в верхней полуплоскости H и дискретной подгруппе Γ группы PSL(2, R ) , действующей свободно разрывно в верхней полуплоскости, то можно определить многоугольник Дирихле как множество точек
Здесь d — гиперболическая метрика в верхней полуплоскости. Метрический фундаментальный многоугольник чаще называют многоугольником Дирихле .
- Этот фундаментальный многоугольник является фундаментальной областью .
- Этот фундаментальный многоугольник является выпуклым в том смысле, что геодезическая , соединяющая любые две точки многоугольника, полностью содержится внутри многоугольника.
- Диаметр меньше или F / Γ равен диаметру H . В частности, замыкание F компактно.
- Если Γ не имеет неподвижных точек в H и H /Γ компактно, то F будет иметь конечное число сторон.
- Каждая сторона многоугольника представляет собой геодезическую дугу.
- Для каждой стороны s многоугольника существует ровно еще одна сторона s ′ такая, что gs = s ′ для некоторого g из Γ. Таким образом, этот многоугольник будет иметь четное количество сторон.
- Множество элементов группы g , соединяющих стороны друг с другом, является образующими группы Γ (заметим, однако, что это множество образующих не обязательно минимально).
- Верхняя полуплоскость замощена замыканием F под действием Γ. То есть, где это закрытие F .
Нормализованный многоугольник [ править ]
В этом разделе, начиная с произвольного многоугольника Дирихле, будет дано описание метода Неванлинны (1953) , разработанного Йостом (2002) , для модификации многоугольника в невыпуклый многоугольник с 4 г эквивалентными вершинами и каноническим сопряжение по бокам. Эта трактовка является аналитическим аналогом классической топологической классификации ориентируемых двумерных многогранников, представленной Зейфертом и Трелфоллом (1934) .
Канонический многоугольник Фрике [ править ]
Учитывая риманову поверхность рода g больше единицы, Фрике описал другой фундаментальный многоугольник, канонический многоугольник Фрике , который является особым примером многоугольника Дирихле. Многоугольник связан со стандартным представлением фундаментальной группы поверхности. Первоначальная конструкция Фрике сложна и описана у Фрике и Кляйна (1897) . Используя теорию квазиконформных отображений Альфорса дал новую, более короткую и и Берса , Кин (1965) точную версию конструкции Фрике. Канонический многоугольник Фрике обладает следующими свойствами:
- Вершины многоугольника Фрике имеют 4 g вершин, все из которых лежат на орбите Γ. Под вершиной понимается точка встречи двух сторон.
- Стороны соединяются в разные пары, так что существует уникальный элемент Γ, переносящий сторону в парную сторону, меняя ориентацию. Поскольку действие Γ сохраняет ориентацию, если одну сторону назвать , то другой из пары можно пометить с противоположной ориентацией .
- Ребра стандартного многоугольника можно расположить так, чтобы список смежных сторон принял вид . То есть пары сторон можно расположить так, чтобы они чередовались таким образом.
- Стороны представляют собой геодезические дуги.
- Каждый из внутренних углов многоугольника Фрике строго меньше π , так что многоугольник строго выпуклый, а сумма этих внутренних углов равна 2 π .
Приведенной выше конструкции достаточно, чтобы гарантировать, что каждая сторона многоугольника является замкнутой (нетривиальной) петлей на римановой поверхности H /Γ. Таким образом, каждая сторона может быть элементом фундаментальной группы. . В частности, фундаментальная группа имеет 2 g -генератора , ровно с одним определяющим ограничением,
- .
Род римановой поверхности H /Γ равен g .
Площадь [ править ]
Площадь стандартного фундаментального многоугольника равна где g — род римановой поверхности (эквивалентно, где 4 g — число сторон многоугольника). Поскольку стандартный многоугольник является представителем H /Γ, общая площадь римановой поверхности равна площади стандартного многоугольника. Формула площади следует из теоремы Гаусса–Бонне и в определенном смысле обобщается через формулу Римана–Гурвица .
Явная форма для стандартных многоугольников [ править ]
Явные выражения могут быть даны для правильного стандартного 4- угольного многоугольника с вращательной симметрией. В этом случае род Риманова поверхность с g -кратной вращательной симметрией, группа может быть задана формулой генераторы . Эти генераторы задаются следующими дробными линейными преобразованиями, действующими в верхней полуплоскости :
для . Параметры задаются
и
и
Можно проверить, что эти генераторы подчиняются ограничению
что дает целостность групповой презентации .
См. также [ править ]
Примечания [ править ]
- ^ См.:
- ^ См.:
- ^ Пример построения сферы из фундаментального многоугольника .
- ^ E. Fedorov (1891) "Симметрія на плоскости" ( Simmetriya na ploskosti , Symmetry in the plane), Записки Императорского С.-Петербургского минералогического общества ( Zapiski Imperatorskova Sankt-Petersburgskova Mineralogicheskova Obshchestva , Proceedings of the Imperial St. Petersburg Mineralogical Society), 2nd series, 28 : 345–390 (in Russian).
- ^ См.:
- ^ Доказательство Вороного имеет то преимущество, что оно обобщается на n измерений: оно показывает, что если транслировать центрально-симметричный выпуклый многогранник тессаллат R н , то в многограннике не более 2(2 н − 1) лица.
- ^ См.:
- ^ См.:
- Кассельс 1997 г.
- Колмогоров и Юкшкевич 2001 , стр. 157–159.
- ↑ Перейти обратно: Перейти обратно: а б с Бердон 1984 г.
- ^ Имаёши и Танигучи, 1992 г.
- ^ Обратите внимание, что простой многоугольник на плоскости с n ≥ 4 вершинами гомеоморфен одному, а значит, и любому выпуклому n -угольнику посредством кусочно-линейного гомеоморфизма, линейного на краях: это следует индукцией по n из наблюдения Макса Дена. что любой простой многоугольник имеет диагональ, то есть внутреннюю хорду между вершинами, поэтому его можно разбить на более мелкие многоугольники; см. Гуггенхаймер (1977) . Для правильного 4 -угольника спаривание сторон можно сделать линейным, перепараметризовав треугольники, состоящие из центра и одной стороны каждой пары сторон.
- ^ Йост 2002 , стр. 47–57.
- ^ Шастри 2011
- ^ Фарб и Маргалит, 2012 г.
- ↑ Перейти обратно: Перейти обратно: а б Альфорс 2006 , стр. 67–68.
- ^ Фарб и Маргалит 2012 , стр. 230–236
Ссылки [ править ]
- Альфорс, Ларс В. (2006), Лекции по квазиконформным отображениям , Серия университетских лекций, том. 38 (второе изд.), Американское математическое общество , ISBN. 978-0-8218-3644-6
- Аппелл, П.; Гурса, Э.; Фату, П. (1930), Теория алгебраических функций переменной, Том II, Автоморфные функции , Готье-Вилар, стр. 102–154
- Бамба, РП; Давенпорт, Х. (1952), «Покрытие n-мерного пространства сферами», J. London Math. Соц. , 27 (2): 224–229, doi : 10.1112/jlms/s1-27.2.224
- Бердон, Алан Ф. (1983), Геометрия дискретных групп , Springer-Verlag, ISBN 978-0-387-90788-8
- Бердон, Алан Ф. (1984), Учебник по римановым поверхностям , Серия лекций Лондонского математического общества, том. 78, Издательство Кембриджского университета , ISBN 978-0-521-27104-2
- Бонк, Мариус; Шрамм, Одед (2000), "Вложения гиперболических пространств Громова", Геом. Функц. Анальный. , 10 (2): 266–306, CiteSeerX 10.1.1.47.7874 , doi : 10.1007/s000390050009
- Бёрёчки, Карой младший (2004), Конечная упаковка и покрытие , Cambridge Tracts in Mathematics, vol. 154, Издательство Кембриджского университета , ISBN 978-0-521-80157-7
- Бурдон, Марк; Пажо, Эрве (2002), «Квазиконформная геометрия и гиперболическая геометрия», у Марка Бургера; Алессандра Иоцци (ред.), Жесткость в динамике и геометрии , Springer, стр. 1–17, ISBN 978-3-540-43243-2
- Бузер, Питер (1992), Геометрия и спектры компактных римановых поверхностей , Progress in Mathematics, vol. 106, Биркхойзер, номер номера : 10.1007/978-0-8176-4992-0 , ISBN. 978-0-8176-3406-3
- Кассельс, JWS (1997), «IX. Упаковки», Введение в геометрию чисел , Классика математики, Springer-Verlag, ISBN 978-3-540-61788-4
- Коксетер, HS M (1962), «Классификация зоноэдров с помощью проективных диаграмм», J. Math. Приложение Pures. , 41 : 137–156
- Коксетер, HSM ; Мозер, WOJ (1980), Генераторы и соотношения для дискретных групп , вып. 14 (Четвертое издание. Результаты математики и ее пограничных областей под ред.), Springer-Verlag, ISBN 978-3-540-09212-4
- Эгглстон, Х.Г. (1958), Выпуклость , Кембриджские трактаты по математике и математической физике, том. Издательство Кембриджского университета
- Фарб, Бенсон ; Маргалит, Дэн (2012), Учебник по отображению групп классов , Princeton Mathematical Series, vol. 49, Издательство Принстонского университета , ISBN 978-0-691-14794-9
- Фаркас, Гершель М.; Кра, Ирвин (1980), Riemann Surfaces , Springer-Verlag, ISBN 978-0-387-90465-8
- Фенхель, Вернер ; Нильсен, Якоб (2003), Разрывные группы изометрий в гиперболической плоскости , Исследования де Грюйтера по математике, том. 29, Вальтер де Грюйтер, ISBN 978-3-11-017526-4
- Фрике, Роберт; Кляйн, Феликс (1897), Лекции по теории автоморфных функций, Том 1: Основы теории групп , Тойбнер, стр. 236–237, 295–320
- Грюнбаум, Бранко ; Шепард, GC (1987), Плитки и узоры , WH Freeman, ISBN 978-0-7167-1193-3
- Гуггенхаймер, Х. (1977), «Теорема о кривой Жордана и неопубликованная рукопись Макса Дена» (PDF) , Архив истории точных наук , 17 (2): 193–200, CiteSeerX 10.1.1.374.1893 , doi : 10.1007/БФ02464980 , ДЖСТОР 41133486 , МР 0532231
- Хирш, Моррис В. (1994), Дифференциальная топология , Тексты для аспирантов по математике, том. 33, Шпрингер-Верлаг, ISBN 978-0-387-90148-0
- Имаёси, Ю.; Танигучи, М. (1992), Введение в пространства Тейхмюллера , Springer-Verlag, ISBN 978-0-387-70088-5
- Иверсен, Биргер (1992), Гиперболическая геометрия , Студенческие тексты Лондонского математического общества, том. 25, Издательство Кембриджского университета , ISBN 978-0-521-43508-6
- Йост, Юрген (2002), Компактные римановы поверхности (2-е изд.), Springer-Verlag, ISBN 978-3-540-43299-9
- Капович, Илья; Бенакли, Надя (2002), «Границы гиперболических групп», Комбинаторная и геометрическая теория групп , Contemp. Матем., вып. 296, Американское математическое общество , стр. 39–93.
- Кин, Линда (1965), «Канонические многоугольники для конечно порожденных фуксовых групп», Acta Math. , 115 : 1–16, doi : 10.1007/bf02392200
- Кин, Линда (1966), «Внутренние модули на римановых поверхностях», Ann. математики. , 84 (3): 404–420, номер документа : 10.2307/1970454 , JSTOR 1970454.
- Колмогоров А.Н.; Юкшкевич А.П., ред. (2001), Математика XIX века: математическая логика, алгебра, теория чисел, теория вероятностей , Springer, ISBN 978-3-7643-6441-0
- Лехто, Олли (1987), Однолистные функции и пространства Тейхмюллера , Тексты для аспирантов по математике, том. 109, Спрингер Верлаг, ISBN 978-0-387-96310-5
- Люстерник, Луизиана (1966), Выпуклые фигуры и многогранники , перевод Дональда Л. Барнетта, Бостон: DC Heath and Co.
- Неванлинна, Рольф (1953), Униформизация , Основные положения математических наук в отдельных изложениях с особым рассмотрением областей применения (на немецком языке), vol. 64, Шпрингер Верлаг
- Зайферт, Герберт; Трелфолл, Уильям (1934), Учебник топологии , Чистая и прикладная математика, том. 89, перевод Майкла А. Голдмана, Academic Press, ISBN 978-0-12-634850-7
- Шастри, Анант Р. (2011), Элементы дифференциальной топологии , CRC Press, ISBN 978-1-4398-3160-1
- Сигел, CL (1971), Темы теории комплексных функций, Vol. II. Автоморфные функции и абелевы интегралы в переводе А. Шеницера; М. Треткофф, Wiley-Interscience
- Стиллвелл, Джон (1992), Геометрия поверхностей , Universitext, Springer-Verlag, ISBN 978-0-387-97743-0
- Цзун, Чуаньмин (2014), «Упаковка, покрытие и мозаика в двумерных пространствах», Expositiones Mathematicae , 32 (4): 297–364, doi : 10.1016/j.exmath.2013.12.002









































