Биголоморфизм
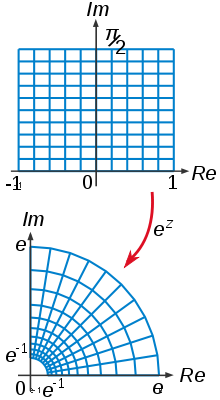
В математической теории функций одной или нескольких комплексных переменных , а также в алгебраической геометрии биголоморфизмом голоморфна или биголоморфной функцией называется биективная голоморфная функция которой , обратная также комплексной .
Формальное определение [ править ]
Формально биголоморфная функция — это функция определенное на открытом U подмножестве -мерное комплексное пространство C н со значениями в C н который голоморфен и взаимно однозначен , такой, что его образ является открытым множеством в С н и обратное также голоморфен . В более общем смысле U и V могут быть комплексными многообразиями . Как и в случае с функциями одной комплексной переменной, достаточным условием того, чтобы голоморфное отображение было биголоморфным своему образу, является то, что отображение инъективно, и в этом случае обратное отображение также голоморфно (например, см. Gunning 1990, теорема I. 11 или следствие E.10 стр. 57).
Если существует биголоморфизм мы говорим, что U и V или биголоморфно эквивалентны что они биголоморфны .
Теорема Римана об отображении ее обобщения и
Если всякое односвязное открытое множество, кроме всей комплексной плоскости, биголоморфно единичному кругу (это теорема об отображении Римана ). Ситуация совершенно иная в высших измерениях. Например, открытые единичные шары и открытые единичные полидиски не являются биголоморфно эквивалентными для На самом деле не существует даже собственной голоморфной функции, переводящей одно в другое.
Альтернативные определения [ править ]
В случае отображений f : U → C, определенных на открытом подмножестве U комплексной плоскости C , некоторые авторы (например, Freitag 2009, определение IV.4.1) определяют конформное отображение как инъективное отображение с ненулевой производной, т. е. f '( z )≠ 0 для каждого z в U . Согласно этому определению, отображение f : U → C конформно тогда и только тогда, когда f : U → f ( U ) биголоморфно. Обратите внимание, что в определении биголоморфизмов ничего не предполагается об их производных, поэтому эта эквивалентность содержит утверждение о том, что гомеоморфизм, который является комплексно дифференцируемым, на самом деле должен иметь ненулевую производную всюду. Другие авторы (например, Conway 1978) определяют конформное отображение как отображение с ненулевой производной, но не требуя, чтобы оно было инъективным. Согласно этому более слабому определению, конформное отображение не обязательно должно быть биголоморфным, даже если оно локально биголоморфно, например, по теореме об обратной функции. Например, если f : U → U определяется как f ( z ) = z 2 при U = C – {0}, то f конформно на U , поскольку его производная f '( z ) = 2 z ≠ 0, но не биголоморфна, поскольку равна 2-1.
Ссылки [ править ]
- Конвей, Джон Б. (1978). Функции одной комплексной переменной . Спрингер-Верлаг. ISBN 3-540-90328-3 .
- Д'Анджело, Джон П. (1993). Некоторые комплексные переменные и геометрия реальных гиперповерхностей . ЦРК Пресс. ISBN 0-8493-8272-6 .
- Пятница, Эберхард; Бусам, Рольф (2009). Комплексный анализ . Издательство Спрингер. ISBN 978-3-540-93982-5 .
- Ганнинг, Роберт К. (1990). Введение в голоморфные функции многих переменных, Vol. II . Уодсворт. ISBN 0-534-13309-6 .
- Кранц, Стивен Г. (2002). Теория функций многих комплексных переменных . Американское математическое общество. ISBN 0-8218-2724-3 .
Эта статья включает в себя материал из биголоморфно эквивалентного сайта PlanetMath , который доступен под лицензией Creative Commons Attribution/Share-Alike License .






