Равносторонний пятиугольник

В геометрии равносторонний пятиугольник — это многоугольник в евклидовой плоскости с пятью сторонами одинаковой длины . Его пять углов при вершинах могут принимать различные наборы значений, что позволяет ему образовывать семейство пятиугольников. Напротив, правильный пятиугольник уникален, потому что он равносторонний и, более того, равноугольный (его пять углов равны; мера равна 108 градусам ).

Четырех пересекающихся равных окружностей, расположенных в замкнутую цепочку, достаточно, чтобы определить выпуклый равносторонний пятиугольник. Центр каждого круга является одной из четырех вершин пятиугольника. Оставшаяся вершина определяется одной из точек пересечения первого и последнего круга цепочки.

Примеры

Простой				Коллинеарные края	Сложный многоугольник
Выпуклый		Вогнутый		Коллинеарные края	Сложный многоугольник
Правильный пятиугольник 108° ( внутренние углы )	Соседние прямые углы (60° 150° 90° 90° 150°)	Отраженный правильный пятиугольник (36° 252° 36° 108° 108°)	Двенадцатиугольный универсальный ^[1] (30° 210° 60° 90° 150°)	Выродиться в трапецию (120° 120° 60° 180° 60°)	Обычная звезда пентаграмма (36°)	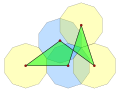Пересекающиеся (36° 108° −36° −36° 108°)
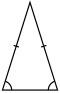				Выродиться в треугольник (≈28.07° 180° ≈75.96° ≈75.96° 180°)	Самопересекающийся	Выродиться (перекрытие ребра-вершины)

Внутренние углы выпуклого равностороннего пятиугольника.

Когда выпуклый равносторонний пятиугольник разбивается на треугольники, два из них кажутся равнобедренными (треугольники оранжевого и синего цвета), а другой имеет более общий вид (треугольник зеленого цвета). Будем считать, что нам даны смежные углы $\alpha$ и $\beta$ .

По закону синусов длина линии , разделяющей зеленый и синий треугольники, равна:

a=2\sin \left({\frac {\beta }{2}}\right).

Квадрат длины линии, разделяющей оранжевый и зеленый треугольники, равен:

{\begin{aligned}b^{2}&=1+a^{2}-2(1)(a)\cos \left(\alpha -{\frac {\pi }{2}}+{\frac {\beta }{2}}\right)\\&=1+4\sin ^{2}\left({\frac {\beta }{2}}\right)-4\sin \left({\frac {\beta }{2}}\right)\sin \left(\alpha +{\frac {\beta }{2}}\right).\\\end{aligned}}

По закону косинусов косинус δ можно увидеть из рисунка:

\cos(\delta )={\frac {1^{2}+1^{2}-b^{2}}{2(1)(1)}}\ .

Упрощая, δ получается как функция от α и β:

\delta =\arccos \left[\cos(\alpha )+\cos(\beta )-\cos(\alpha +\beta )-{\frac {1}{2}}\right].

Остальные углы пятиугольника можно найти геометрически: оставшиеся углы оранжевого и синего треугольников легко найти, заметив, что два угла равнобедренного треугольника равны, а сумма всех трех углов равна 180 °. Затем $\epsilon ,\gamma ,$ а два оставшихся угла зеленого треугольника можно найти из четырех уравнений, утверждающих, что сумма углов пятиугольника равна 540°, сумма углов зеленого треугольника равна 180°, угол $\gamma$ представляет собой сумму трех его компонент, а угол $\epsilon$ представляет собой сумму двух его составляющих.

Вписанный он имеет равные пятиугольник является равноугольным тогда и только тогда, когда стороны и, следовательно, является правильным. Аналогично, касательный пятиугольник является равносторонним тогда и только тогда, когда он имеет равные углы и, следовательно, является правильным. ^[2]

Укладка плитки

Есть два бесконечных семейства равносторонних выпуклых пятиугольников, покрывающих плоскость : одно имеет два смежных дополнительных угла , а другое - два несмежных дополнительных угла. Некоторые из этих пятиугольников могут располагаться плиткой более чем одним способом, и есть один спорадический пример равностороннего пятиугольника, который может располагаться плиткой на плоскости, но не принадлежит ни к одному из этих двух семейств; его углы составляют примерно 89°16', 144°32,5', 70°55', 135°22' и 99°54,5', двух дополнительных нет. ^[3]

Двумерное отображение

Равносторонние пятиугольники могут пересекаться либо не пересекаться вообще, либо один, два или пять раз. Те, которые не пересекаются сами по себе, называются простыми , и их можно классифицировать как выпуклые или вогнутые. Здесь мы используем термин «звездчатый» для обозначения тех, которые пересекаются дважды или пять раз. В этом разделе мы исключаем равносторонние пятиугольники, пересекающие себя ровно один раз.

Учитывая, что мы исключаем пятиугольники, которые пересекаются один раз, мы можем построить остальное как функцию двух переменных в двумерной плоскости . Каждая пара значений (α, β) отображается в одну точку плоскости, а также в один пятиугольник.

Периодичность значений α и β и условие α ≥ β ≥ δ позволяют ограничить размер отображения. В плоскости с координатными осями α и β уравнение α = β представляет собой линию, делящую плоскость на две части (южная граница на рисунке показана оранжевым цветом). Уравнение δ = β в виде кривой делит плоскость на разные участки (северная граница показана синим цветом).

Обе границы охватывают непрерывную область плоскости, точки которой соответствуют уникальным равносторонним пятиугольникам. Точки за пределами региона просто сопоставляются с повторяющимися пятиугольниками, то есть пятиугольниками, которые при повороте или отражении могут соответствовать другим, уже описанным. Пятиугольники, которые совпадают точно с этими границами, имеют линию симметрии .

Внутри области уникальных отображений находятся три типа пятиугольников: звездчатые, вогнутые и выпуклые, разделенные новыми границами.

звездчатый

Звездчатые пятиугольники имеют стороны , пересекающиеся с другими. Типичным примером этого типа пятиугольника является пентаграмма . Условием того, чтобы пятиугольник был звездчатым или самопересекающимся, является наличие 2α + β ≤ 180°. Итак, на карте линия 2α + β = 180° (показана оранжевым цветом на севере) является границей между областями звёздчатых и незвёздчатых пятиугольников. Пятиугольники, которые соответствуют точно этой границе, имеют вершину, касающуюся другой стороны.

Вогнутый

Вогнутые пятиугольники представляют собой незвездчатые пятиугольники, имеющие по крайней мере один угол больше 180°. Первый угол, который открывается шире 180 °, — это γ, поэтому уравнение γ = 180 ° (граница, показанная зеленым справа) представляет собой кривую, которая является границей областей вогнутых пятиугольников и других областей, называемых выпуклыми. Пятиугольники, которые соответствуют точно этой границе, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, что напоминает пятиугольник, перерожденный в четырехугольник .

Выпуклый

пятиугольников У выпуклых все пять углов меньше 180° и ни одна сторона не пересекается с другими. Типичным примером этого типа пятиугольника является правильный пятиугольник .

Ссылки

^ Грюнбаум, Б. и Шепард, GC, 1979. Спиральные мозаики и универсалии. Обучение математике, 88, стр. 50-51. Спиральные плитки, Пауль Гайлюнас
^ Де Вильерс, Майкл, «Равноугольные циклические и равносторонние описанные многоугольники», Mathematical Gazette 95, март 2011 г., 102–107.
^ Шатшнайдер, Дорис (1978), «Разбиение плоскости равными пятиугольниками», Mathematics Magazine , 51 (1): 29–44, doi : 10.1080/0025570X.1978.11976672 , JSTOR 2689644 , MR 0493766

[1] Грюнбаум, Б. и Шепард, GC, 1979. Спиральные мозаики и универсалии. Обучение математике, 88, стр. 50-51. Спиральные плитки, Пауль Гайлюнас

[2] Де Вильерс, Майкл, «Равноугольные циклические и равносторонние описанные многоугольники», Mathematical Gazette 95, март 2011 г., 102–107.

[3] Шатшнайдер, Дорис (1978), «Разбиение плоскости равными пятиугольниками», Mathematics Magazine , 51 (1): 29–44, doi : 10.1080/0025570X.1978.11976672 , JSTOR 2689644 , MR 0493766

[1]

[2]

[3]