Евклидово разбиение выпуклыми правильными многоугольниками

Пример периодических мозаик
Обычная плитка имеет один тип регулярной грани.	Полурегулярная или равномерная мозаика имеет один тип вершин , но два или более типов граней.
k имеет -однородная мозаика k типов вершин и два или более типов правильных граней.	Мозаика без от края до края может иметь правильные грани разного размера.

евклидовой плоскости Замощения выпуклыми правильными многоугольниками широко использовались с древности. Первой систематической математической трактовкой была работа Кеплера в его «Harmonices Mundi» ( лат . «Гармония мира» , 1619).

Обозначения евклидовых мозаик

Евклидовы мозаики обычно называют в честь обозначений Канди и Роллетта. ^[1] Это обозначение представляет (i) количество вершин, (ii) количество многоугольников вокруг каждой вершины (расположенных по часовой стрелке) и (iii) количество сторон каждого из этих многоугольников. Например: 3 ⁶; 3 ⁶; 3 ⁴.6 говорит нам, что существует 3 вершины с 2 разными типами вершин, поэтому это замощение будет классифицироваться как «3-однородное (2-типы вершин)». Сломанная, 3 ⁶; 3 ⁶ (оба разного класса транзитивности), или (3 ⁶) ², говорит нам, что есть 2 вершины (обозначаются верхним индексом 2), каждая из которых имеет 6 равносторонних 3-сторонних многоугольников (треугольников). С конечной вершиной 3 ⁴.6, еще 4 смежных равносторонних треугольника и один правильный шестиугольник.

Однако у этого обозначения есть две основные проблемы, связанные с неоднозначной конформацией и уникальностью. ^[2] Во-первых, когда речь идет о k-однородных мозаиках, обозначения не объясняют отношений между вершинами. Это делает невозможным создание покрытой плоскости, используя только обозначения. А во-вторых, некоторые мозаики имеют одинаковую номенклатуру, они очень похожи, но можно заметить, что взаимное расположение шестиугольников различно. Следовательно, вторая проблема заключается в том, что эта номенклатура не уникальна для каждой тесселяции.

Чтобы решить эти проблемы, используются обозначения ГомДжау-Хогга. ^[3] представляет собой слегка измененную версию исследования и обозначений, представленных в 2012 году, ^[2] о создании и номенклатуре тесселяций и двухслойных сеток. Антверпен v3.0, ^[4] бесплатное онлайн-приложение позволяет бесконечно генерировать мозаику из правильных многоугольников с помощью набора этапов размещения фигур и итеративных операций вращения и отражения, полученных непосредственно из нотации ГомДжау-Хогга.

Регулярные мозаики

Следуя Грюнбауму и Шепарду (раздел 1.3), замощение называется регулярным , если группа симметрии замощения действует транзитивно на флаги замощения, где флагом является тройка, состоящая из взаимно инцидентной вершины , ребра и плитки разбиения. укладка плитки. Это означает, что для каждой пары флагов существует операция симметрии, отображающая первый флаг на второй. Это эквивалентно мозаике, представляющей собой мозаику от края до края равными правильными многоугольниками. Должно быть шесть равносторонних треугольников , четыре квадрата или три правильных шестиугольника в вершине, что дает три правильных мозаики .

Регулярные мозаики (3)
п6м, *632		п4м, *442

К&Р: 3 ⁶ GJ-H: 3/м30/р(ч2) ( т = 1, е = 1)	К&Р: 6 ³ GJ-H: 6/м30/р(ч1) ( т = 1, е = 1)	К&Р: 4 ⁴ GJ-H: 4/м45/р(ч1) ( т = 1, е = 1)

C&R: обозначения Канди и Роллета.
GJ-H: обозначение GomJau-Hogg

Архимедовы, равномерные или полуправильные мозаики

Вершинная транзитивность означает, что для каждой пары вершин существует операция симметрии, переводящая первую вершину во вторую. ^[5]

Если требование транзитивности флагов ослабляется до требования транзитивности вершин, при этом сохраняется условие, что мозаика является сквозной, возможны восемь дополнительных мозаик, известных как архимедовы , равномерные или полуправильные мозаики. Обратите внимание, что существуют две зеркальные формы (энантиоморфные или киральные ) формы 3. ⁴.6 (взносая шестиугольная) черепица, только одна из которых показана в следующей таблице. Все остальные правильные и полуправильные замощения ахиральны.

Однородные плитки (8)
п6м, *632
К&Р: 3.12 ² GJ-H: 12-3/м30/р(ч3) ( т = 2, е = 2) т {6,3}	C&R: 3.4.6.4 ГЮ-Х: 6-4-3/м30/р(c2) ( т = 3, е = 2) рр {3,6}	C&R: 4.6.12 GJ-H: 12-6,4/м30/р(с2) ( т = 3, е = 3) тр {3,6}	К&Р: (3,6) ² ГЮ-Х: 6-3-6/м30/р(v4) ( т = 2, е = 1) р {6,3}
C&R: 4,8 ² ГЮ-Х: 8-4/м90/р(h4) ( т = 2, е = 2) т {4,4}	К&Р: 3 ².4.3.4 ГЮ-Х: 4-3-3,4/r90/r(h2) ( т = 2, е = 2) с {4,4}	К&Р: 3 ³.4 ² ГД-Х: 4-3/м90/р(ч2) ( т = 2, е = 3) {3,6}: и	К&Р: 3 ⁴.6 ГЮ-Х: 6-3-3/r60/r(h5) ( т = 3, е = 3) ср {3,6}

C&R: обозначения Канди и Роллета.
GJ-H: обозначение GomJau-Hogg

Грюнбаум и Шепард различают описание этих мозаик как архимедово , поскольку оно относится только к локальному свойству одинакового расположения плиток вокруг каждой вершины, и как единообразное , поскольку относится к глобальному свойству вершинной транзитивности. Хотя они дают один и тот же набор мозаик на плоскости, в других пространствах существуют архимедовы мозаики, которые не являются однородными.

Плосковершинные мозаики

Существует 17 комбинаций правильных выпуклых многоугольников, образующих 21 тип плосковершинных мозаик . ^[6]^[7] Полигоны в них встречаются в точках без разрывов или перекрытий. Если перечислять их вершинные фигуры , то у одного будет 6 полигонов, у троих — 5 полигонов, у семи — 4 полигона, а у десяти — 3 полигона. ^[8]

Как подробно описано в разделах выше, три из них могут образовывать правильные мозаики (6 ³, 4 ⁴, 3 ⁶), и еще восемь могут составлять полуправильные или архимедовы замощения , (3.12.12, 4.6.12, 4.8.8, (3.6) ², 3.4.6.4, 3.3.4.3.4, 3.3.3.4.4, 3.3.3.3.6). Четыре из них могут существовать в более высоких k -однородных мозаиках (3.3.4.12, 3.4.3.12, 3.3.6.6, 3.4.4.6), тогда как шесть нельзя использовать для полного замощения плоскости правильными многоугольниками без пробелов и перекрытий - они полностью замощить пространство только при включении неправильных многоугольников (3.7.42, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 5.5.10). ^[9]

Плосковершинные мозаики
6	3 ⁶
5	3.3.4.3.4	3.3.3.4.4	3.3.3.3.6
4	3.3.4.12	3.4.3.12	3.3.6.6	(3.6) ²	3.4.4.6	3.4.6.4	4 ⁴
3	3.7.42	3.8.24	3.9.18	3.10.15	3.12.12	4.5.20	4.6.12	4.8.8	5.5.10	6 ³

k - однородные мозаики

Такие периодические мозаики можно классифицировать по количеству орбит вершин, ребер и плиток. Если существует $k$ орбит вершин, мозаика называется $k$ -равномерной или $k$ -изогональной; если существует $t$ орбит плиток, то $t$ -изоэдра; если существует $e$ орбит ребер, то $e$ -изотоксал.

k -однородные мозаики с одинаковыми фигурами вершин можно дополнительно идентифицировать по симметрии группы обоев .

К 1-однородным мозаикам относятся 3 правильных мозаики и 8 полуправильных мозаик с 2 и более типами граней правильных многоугольников. Существует 20 2-однородных мозаик, 61 3-однородных мозаики, 151 4-однородных мозаики, 332 5-однородных мозаики и 673 6-однородных мозаики. Каждый из них может быть сгруппирован по числу m различных фигур вершин, которые также называются m -архимедовыми мозаиками. ^[10]

Наконец, если количество типов вершин такое же, как и однородность ( m = k ниже), то мозаика называется Кротенхердтом . В общем, однородность больше или равна количеству типов вершин ( m ≥ k ), поскольку разные типы вершин обязательно имеют разные орбиты, но не наоборот. Полагая m = n = k , существует 11 таких мозаик для n = 1; 20 таких мозаик для n = 2; 39 таких разбиений для n = 3; 33 таких мозаики для n = 4; 15 таких мозаик для n = 5; 10 таких мозаик для n = 6; и 7 таких мозаик для n = 7.

Ниже приведен пример 3-однородной мозаики:

Цветная 3-однородная плитка № 57 из 61
сторонами, желтыми треугольниками, красными квадратами (многоугольниками)	по 4-изоэдральным позициям, 3 заштрихованным цветам треугольников (по орбитам)

k - равномерный, m - количество архимедовых мозаик ^[11]^[12]
		м -Архимедова
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	≥ 15	Общий
к -равномерный	1	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	11
	2	0	20	0	0	0	0	0	0	0	0	0	0	0	0	0	20
	3	0	22	39	0	0	0	0	0	0	0	0	0	0	0	0	61
	4	0	33	85	33	0	0	0	0	0	0	0	0	0	0	0	151
	5	0	74	149	94	15	0	0	0	0	0	0	0	0	0	0	332
	6	0	100	284	187	92	10	0	0	0	0	0	0	0	0	0	673
	7	0	?	?	?	?	?	7	0	0	0	0	0	0	0	0	1472
	8	0	?	?	?	?	?	20	0	0	0	0	0	0	0	0	2850
	9	0	?	?	?	?	?	?	8	0	0	0	0	0	0	0	5960
	10	0	?	?	?	?	?	?	27	0	0	0	0	0	0	0	11866
	11	0	?	?	?	?	?	?	?	1	0	0	0	0	0	0	24459
	12	0	?	?	?	?	?	?	?	?	0	0	0	0	0	0	49794
	13	0	?	?	?	?	?	?	?	?	?	?	?	0	0	0	103082
	14	0	?	?	?	?	?	?	?	?	?	?	?	?	0	0	?
	≥ 15	0	?	?	?	?	?	?	?	?	?	?	?	?	?	0	?
	Общий	11	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	0	∞

2-однородные мозаики

Существует двадцать (20) 2-однородных мозаик евклидовой плоскости. (также называемые 2- изогональными мозаиками или полуправильными мозаиками ) ^[5]^: 62-67 ^[13]^[14] Типы вершин указаны для каждой. Если два мозаики имеют одинаковые два типа вершин, им присваиваются индексы 1,2.

2-однородные мозаики (20)
п6м, *632						п4м, *442
[3 ⁶; 3 ².4.3.4] 3-4-3/м30/об(с3) ( т = 3, е = 3)	[3.4.6.4; 3 ².4.3.4] 6-4-3,3/м30/об(ч1) ( т = 4, е = 4)	[3.4.6.4; 3 ³.4 ²] 6-4-3-3/м30/р(h5) ( т = 4, е = 4)	[3.4.6.4; 3.4 ².6] 6-4-3,4-6/м30/р(с4) ( т = 5, е = 5)	[4.6.12; 3.4.6.4] 12-4,6-3/м30/об(с3) ( т = 4, е = 4)	[3 ⁶; 3 ².4.12] 12-3,4-3/м30/р(с3) ( т = 4, е = 4)	[3.12.12; 3.4.3.12] 12-0,3,3-0,4/м45/м(ч1) ( т = 3, е = 3)
п6м, *632	стр6, 632	стр6, 632	см, 2*22	пмм, *2222	см, 2*22	пмм, *2222
[3 ⁶; 3 ².6 ²] 3-6/м30/об(с2) ( т = 2, е = 3)	[3 ⁶; 3 ⁴.6] ₁ 6-3,3-3/м30/об(ч1) ( т = 3, е = 3)	[3 ⁶; 3 ⁴.6] ₂ 6-3-3,3-3/r60/r(h8) ( т = 5, е = 7)	[3 ².6 ²; 3 ⁴.6] 6-3/м90/р(ч1) ( т = 2, е = 4)	[3.6.3.6; 3 ².6 ²] 6-3,6/м90/р(ч3) ( т = 2, е = 3)	[3.4 ².6; 3.6.3.6] ₂ 6-3,4-6-3,4-6,4/м90/р(с6) ( т = 3, е = 4)	[3.4 ².6; 3.6.3.6] ₁ 6-3,4/м90/р(ч4) ( т = 4, е = 4)
п4г, 4*2	пгг, 22×	см, 2*22	см, 2*22	пмм, *2222	см, 2*22
[3 ³.4 ²; 3 ².4.3.4] ₁ 4-3,3-4,3/р90/м(ч3) ( т = 4, е = 5)	[3 ³.4 ²; 3 ².4.3.4] ₂ 4-3,3,3-4,3/r(c2)/r(h13)/r(h45) ( т = 3, е = 6)	[4 ⁴; 3 ³.4 ²] ₁ 4-3/м(h4)/м(h3)/r(h2) ( т = 2, е = 4)	[4 ⁴; 3 ³.4 ²] ₂ 4-4-3-3/м90/р(h3) ( т = 3, е = 5)	[3 ⁶; 3 ³.4 ²] ₁ 4-3,4-3,3/м90/р(ч3) ( т = 3, е = 4)	[3 ⁶; 3 ³.4 ²] ₂ 4-3-3-3/m90/r(h7)/r(h5) ( т = 4, е = 5)

Высшие k -однородные мозаики

k -однородные мозаики пронумерованы до 6. Существует 673 6-однородных мозаики евклидовой плоскости. Поиск Брайана Галебаха воспроизвел список Кротенхердта из 10 6-однородных мозаик с 6 различными типами вершин, а также обнаружил 92 из них с 5 типами вершин, 187 из них с 4 типами вершин, 284 из них с 3 типами вершин и 100 с 2 типами вершин. типы вершин.

Фрактализация k -однородных мозаик

Существует много способов создания новых k -однородных мозаик из старых k -однородных мозаик. Например, обратите внимание, что 2-однородная [3.12.12; 3.4.3.12] замощение имеет квадратную решетку, 4(3-1)-однородную [343.12; (3.12 ²)3] имеет курносую квадратную решетку и 5(3-1-1)-однородную [334.12; 343,12; (3.12.12)3] замощение имеет вытянутую треугольную решетку. Эти однородные мозаики более высокого порядка используют ту же решетку, но обладают большей сложностью. Фрактализационная основа этих разбиений следующая: ^[15]

	Треугольник	Квадрат	Шестиугольник	рассеченный Додекагон
Форма
Фрактализация

Длины сторон расширены в раз. $2+{\sqrt {3}}$ .

Аналогично это можно сделать, взяв в основу усеченную тригексагональную мозаику с соответствующим расширением $3+{\sqrt {3}}$ .

	Треугольник	Квадрат	Шестиугольник	рассеченный Додекагон
Форма
Фрактализация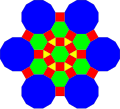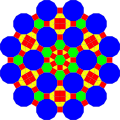

Примеры фрактализации

	Усеченная шестиугольная плитка	Усеченная трехгексагональная плитка
Фрактализация

Плитки, не прилегающие к краю

Выпуклые правильные многоугольники также могут образовывать плоские мозаики, которые не являются смежными. Такие мозаики можно рассматривать как неправильные многоугольники со смежными коллинеарными краями.

Существует семь семейств изогональных плиток, каждое из которых имеет действительный параметр, определяющий перекрытие сторон соседних плиток или соотношение длин ребер разных плиток. Два семейства создаются из смещенного квадрата, прогрессивного или зигзагообразного положения. Грюнбаум и Шепард называют эти мозаики однородными , хотя это противоречит определению однородности Коксетера, которое требует наличия правильных многоугольников от края до края. ^[16] Такие изогональные мозаики на самом деле топологически идентичны однородным мозаикам, но имеют другие геометрические пропорции.

Периодические изогональные замощения выпуклыми правильными многоугольниками без ребра
1	2	3	4	5	6	7
Ряды квадратов со смещением по горизонтали		Ряды треугольников со смещением по горизонтали	Укладка квадратами	Три шестиугольника окружают каждый треугольник	Каждый шестиугольник окружен шестью треугольниками.	Треугольники трех размеров
см (2*22)	р2 (2222)	см (2*22)	п4м (*442)	п6 (632)		п3 (333)
Шестиугольная плитка		Квадратная плитка	Укладка плитки усеченным квадратом	Усеченная шестиугольная плитка	Шестиугольная плитка	Трехгексагональная плитка

См. также

Ссылки

^ Канди, HM; Роллетт, AP (1981). Математические модели; . Стрэдброк (Великобритания): Tarquin Publications.
^ Jump up to: ^а ^б Гомес-Хореги, Валентин др.; Отеро, Сезар; и др. (2012). «Генерация и номенклатура тесселяций и двухслойных сеток» . Журнал строительной техники . 138 (7): 843–852. doi : 10.1061/(ASCE)ST.1943-541X.0000532 . hdl : 10902/5869 .
^ Гомес-Хореги, Валентин; Хогг, Харрисон; и др. (2021). «Нотация ГомДжау-Хогга для автоматического создания k-равномерных тесселяций с помощью ANTWERP v3.0» . Симметрия . 13 (12): 2376. Бибкод : 2021Symm...13.2376G . дои : 10.3390/sym13122376 . hdl : 10902/23907 .
^ Хогг, Харрисон; Гомес-Хореги, Валентин. < «Антверпен 3.0» .
^ Jump up to: ^а ^б Кричлоу, К. (1969). Порядок в космосе: справочник по дизайну . Лондон: Темза и Гудзон. стр. 60–61.
^ Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. д. , Джон В. Паркер и сын, стр. 134
^ Тайлинги и узоры , рисунок 2.1.1, стр.60
^ Плитки и узоры , стр.58-69.
^ «Упаковка Пятиугольника-Декагона» . Американское математическое общество . АМС . Проверено 7 марта 2022 г.
^ k - однородные мозаики из правильных многоугольников. Архивировано 30 июня 2015 г. в Wayback Machine, Нильс Леннгрен, 2009 г.
^ «n-равномерные мозаики» . Вероятностьспорт.com . Проверено 21 июня 2019 г.
^ Слоан, Нью-Джерси (ред.). «Последовательность A068599 (Количество n-равномерных мозаик.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 7 января 2023 г.
^ Плитки и узоры , Грюнбаум и Шепард, 1986, стр. 65-67.
^ «В поисках полурегулярных мозаик» (PDF) . Архивировано из оригинала (PDF) 7 мая 2016 г. Проверено 4 июня 2015 г.
^ Чави, Дарра (2014). «МНОГОУГОЛЬНИКИ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ III: ПЛОТНЫЕ ДОДЕКАГОНА». Симметрия-культура и наука . 25 (3): 193–210. S2CID 33928615 .
^ Замощения правильными многоугольниками стр.236

Грюнбаум, Бранко; Шепард, Джеффри К. (1977). «Замощения правильными многоугольниками». Математика. Маг . 50 (5): 227–247. дои : 10.2307/2689529 . JSTOR 2689529 .
Грюнбаум, Бранко; Шепард, GC (1978). «Девяносто один тип изогональных мозаик на плоскости» . Пер. Являюсь. Математика. Соц . 252 : 335–353. дои : 10.1090/S0002-9947-1978-0496813-3 . МР 0496813 .
Деброй, И.; Ландуит, Ф. (1981). «Эквитранзитивные реберные мозаики». Геометрии Дедиката . 11 (1): 47–60. дои : 10.1007/BF00183189 . S2CID 122636363 .
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . WH Фриман и компания. ISBN 0-7167-1193-1 .
Рен, Дин; Рей, Джон Р. (1987). «Граничная характеристика и теорема Пика в архимедовых плоских мозаиках». Дж. Комб. Теория А. 44 (1): 110–119. дои : 10.1016/0097-3165(87)90063-X .
Чави, Д. (1989). «Замощения правильными многоугольниками - II: Каталог мозаик» . Компьютеры и математика с приложениями . 17 : 147–165. дои : 10.1016/0898-1221(89)90156-9 .
Порядок в космосе: справочник по дизайну, Кейт Кричлоу, 1970 г. ISBN 978-0-670-52830-1
Соммервилл, Дункан Макларен Янг (1958). Введение в геометрию n измерений . Дуврские публикации. Глава X: Правильные многогранники
Преа, П. (1997). «Последовательности расстояний и пороги просачивания в архимедовых мозаиках». Матем. Вычислить. Моделирование . 26 (8–10): 317–320. дои : 10.1016/S0895-7177(97)00216-1 .
Кович, Юрий (2011). «Графы типа симметрии платоновых и архимедовых тел» . Математика. Коммун . 16 (2): 491–507.
Пеллисер, Дэниел; Уильямс, Гордон (2012). «Минимальные накрытия архимедовых мозаик, часть 1» . Электронный журнал комбинаторики . 19 (3): #P6. дои : 10.37236/2512 .
Дейл Сеймур и Джилл Бриттон , «Введение в тесселяцию» , 1989 г., ISBN 978-0866514613 , стр. 50–57

Внешние ссылки

Евклидовы и общие связи мозаики:

n-равномерные мозаики , Брайан Галебах
Датч, Стив. «Единые плитки» . Архивировано из оригинала 9 сентября 2006 г. Проверено 9 сентября 2006 г.
Митчелл, К. «Полуправильные плитки» . Проверено 9 сентября 2006 г.
Вайсштейн, Эрик В. «Тесселяция» . Математический мир .
Вайсштейн, Эрик В. «Полурегулярная мозаика» . Математический мир .
Вайсштейн, Эрик В. «Демирегулярная мозаика» . Математический мир .

[1] Канди, HM; Роллетт, AP (1981). Математические модели; . Стрэдброк (Великобритания): Tarquin Publications.

[Gomez-Jauregui_2012-2] Jump up to: ^а ^б Гомес-Хореги, Валентин др.; Отеро, Сезар; и др. (2012). «Генерация и номенклатура тесселяций и двухслойных сеток» . Журнал строительной техники . 138 (7): 843–852. doi : 10.1061/(ASCE)ST.1943-541X.0000532 . hdl : 10902/5869 .

[3] Гомес-Хореги, Валентин; Хогг, Харрисон; и др. (2021). «Нотация ГомДжау-Хогга для автоматического создания k-равномерных тесселяций с помощью ANTWERP v3.0» . Симметрия . 13 (12): 2376. Бибкод : 2021Symm...13.2376G . дои : 10.3390/sym13122376 . hdl : 10902/23907 .

[4] Хогг, Харрисон; Гомес-Хореги, Валентин. < «Антверпен 3.0» .

[Critchlow_1969-5] Jump up to: ^а ^б Кричлоу, К. (1969). Порядок в космосе: справочник по дизайну . Лондон: Темза и Гудзон. стр. 60–61.

[6] Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. д. , Джон В. Паркер и сын, стр. 134

[7] Тайлинги и узоры , рисунок 2.1.1, стр.60

[8] Плитки и узоры , стр.58-69.

[9] «Упаковка Пятиугольника-Декагона» . Американское математическое общество . АМС . Проверено 7 марта 2022 г.

[10] - однородные мозаики из правильных многоугольников. Архивировано 30 июня 2015 г. в Wayback Machine, Нильс Леннгрен, 2009 г.

[11] «n-равномерные мозаики» . Вероятностьспорт.com . Проверено 21 июня 2019 г.

[12] Слоан, Нью-Джерси (ред.). «Последовательность A068599 (Количество n-равномерных мозаик.)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС . Проверено 7 января 2023 г.

[13] Плитки и узоры , Грюнбаум и Шепард, 1986, стр. 65-67.

[14] «В поисках полурегулярных мозаик» (PDF) . Архивировано из оригинала (PDF) 7 мая 2016 г. Проверено 4 июня 2015 г.

[15] Чави, Дарра (2014). «МНОГОУГОЛЬНИКИ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ III: ПЛОТНЫЕ ДОДЕКАГОНА». Симметрия-культура и наука . 25 (3): 193–210. S2CID 33928615 .

[16] Замощения правильными многоугольниками стр.236

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]