Квадратная плитка Тетракис
| Квадратная плитка Тетракис | |
|---|---|
 | |
| Тип | Двойная полуправильная мозаика |
| Лица | треугольник 45-45-90 |
| Диаграмма Кокстера | |
| Группа симметрии | п4м, [4,4], *442 |
| Группа вращения | р4, [4,4] + , (442) |
| Двойной многогранник | Укладка плитки усеченным квадратом |
| Конфигурация лица | Версия 4.8.8 |
| Характеристики | лице-переходный |
В геометрии представляет квадратная мозаика тетракиса собой мозаику евклидовой плоскости . Это квадратная мозаика , каждый квадрат которой разделен на четыре равнобедренных прямоугольных треугольника от центральной точки, образуя бесконечное расположение линий . Его также можно сформировать путем разделения каждого квадрата сетки на два треугольника по диагонали, при этом диагонали чередуются по направлению, или путем наложения двух квадратных сеток, одна из которых повернута на 45 градусов относительно другой и масштабирована с коэффициентом √2 .
Конвей , Бургель и Гудман-Штраусс называют это кискадрильей . [1] представлена операцией kis , которая добавляет центральную точку и треугольники для замены граней квадратной мозаики (кадрили). Ее также называют решеткой Юнион Джека из-за сходства с британским флагом треугольников, окружающих ее вершины восьмой степени. [2]
Он обозначен V4.8.8, потому что каждая грань равнобедренного треугольника имеет два типа вершин: один с 4 треугольниками и два с 8 треугольниками.
Как двойная однородная мозаика
[ редактировать ]Это двойная мозаика усеченной квадратной мозаики , в каждой вершине которой есть один квадрат и два восьмиугольника. [3]
Приложения
[ редактировать ]Часть квадратной плитки тетракиса размером 5 × 9 используется для формирования доски для малагасийской настольной игры Фанорона . В этой игре фишки размещаются на вершинах плитки и перемещаются по краям, захватывая фишки другого цвета, пока одна сторона не захватит все фишки другой стороны. В этой игре вершины мозаики степени 4 и 8 называются соответственно слабыми пересечениями и сильными пересечениями, и это различие играет важную роль в стратегии игры. [4] Подобная доска также используется для бразильской игры «Адуго» и для игры «Заяц и гончие» .
Квадратная плитка тетракиса использовалась для набора памятных почтовых марок, выпущенных Почтовой службой США в 1997 году, с чередующимся рисунком из двух разных марок. По сравнению с более простым узором для треугольных марок, в котором все диагональные перфорации параллельны друг другу, узор тетракис имеет то преимущество, что при сгибе по любой из его перфораций остальные перфорации совпадают друг с другом, что делает возможным повторное сгибание. [5]
Эта плитка также является основой для часто используемых в выстегивании узоров «вертушка», «ветряная мельница» и «разбитая посуда» . [6] [7] [8]
Симметрия
[ редактировать ]Тип симметрии:
- с расцветкой: смм; — примитивная ячейка 8 треугольников, фундаментальная область — 2 треугольника (по 1/2 на каждый цвет)
- с темными треугольниками черного цвета и светлыми белыми: p4g; примитивная ячейка — 8 треугольников, фундаментальная область — 1 треугольник (по 1/2 для черного и белого)
- с краями черного цвета и внутренней частью белого цвета: p4m; примитивная ячейка — 2 треугольника, фундаментальная область — 1/2
Края квадратной мозаики тетракиса образуют симплициальное расположение линий - свойство, которое она разделяет с треугольной мозаикой и мозаикой кисромбилла .
Эти линии образуют оси симметрии группы отражений ( группы обоев которой являются треугольники мозаики [4,4], (*442) или p4m), фундаментальными областями . Эта группа изоморфна , но не совпадает с группой автоморфизмов мозаики, которая имеет дополнительные оси симметрии, делящие треугольники пополам, и имеет полутреугольники в качестве фундаментальных областей.
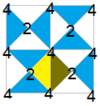
Существует множество небольших индексных подгрупп p4m, симметрии [4,4] ( орбифолдное обозначение *442 ), которые можно увидеть по отношению к диаграмме Кокстера , с узлами, окрашенными в соответствии с линиями отражения, и точками вращения, помеченными численно. Вращательная симметрия показана попеременно белыми и синими областями, при этом одна фундаментальная область для каждой подгруппы закрашена желтым цветом. Отражения при скольжении показаны пунктирными линиями.
Подгруппы могут быть выражены в виде диаграмм Кокстера наряду с диаграммами фундаментальных областей.
| Малые индексные подгруппы p4m, [4,4], (*442) |
|---|
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Конвей, Джон ; Бургель, Хайди; Гудман-Штраус, Хаим (2008), «Глава 21: Именование архимедовых и каталонских многогранников и мозаик», «Симметрии вещей» , А.К. Петерс, с. 288, ISBN 978-1-56881-220-5
- ^ Стивенсон, Джон, «Модель Изинга с антиферромагнитным взаимодействием следующих ближайших соседей: спиновые корреляции и точки разладки», Phys. Rev. B , 1 (11): 4405–4409, doi : 10.1103/PhysRevB.1.4405 .
- ^ Вайсштейн, Эрик В. «Двойная тесселяция» . Математический мир .
- ^ Белл, RC (1983), «Фанорона», Книга настольных игр , Exeter Books, стр. 150–151, ISBN 0-671-06030-9
- ^ Фредериксон, Грег Н. (2006), Расчленения на фортепианных шарнирах , AK Peters, с. 144 .
- ^ Библия квилтинга , Creative Publishing International, 1997, стр. 55, ISBN 9780865732001 .
- ^ Зиман, Нэнси (2011), Одеяло с уверенностью , Krause Publications, стр. 66, ISBN 9781440223556 .
- ^ Фассетт, Каффе (2007), Калейдоскоп лоскутных одеял Каффе Фассетта: двадцать дизайнов от Роуэна для пэчворка и квилтинга , Taunton Press, стр. 96, ISBN 9781561589388 .
Ссылки
[ редактировать ]- Грюнбаум, Бранко и Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . (Глава 2.1: Правильные и однородные мозаики , стр. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 40. ИСБН 0-486-23729-Х .
- Кейт Кричлоу, Порядок в космосе: справочник по дизайну , 1970, стр. 77-76, узор 8