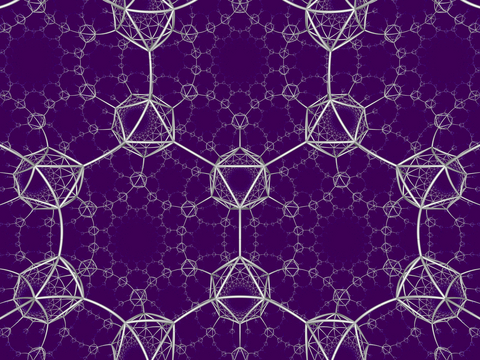
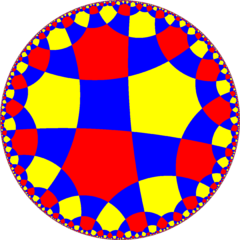
Шестиугольная плитка Орден-6 сотовая

Шестиугольная плитка Орден-6 сотовая
Перспективная проекция из центра модели диска Пуанкаре
Тип	Гиперболические обычные соты Паракомпактный однородный сотовый
Символ Шлефли	{6,3,6} {6,3 ^[3]}
Диаграмма Кокстера	↔ ↔
Клетки	{6,3}
Лица	шестигранник {6}
Краевая фигура	шестигранник {6}
Вершинная фигура	{3,6} или {3 ^[3]}
Двойной	Самодвойственный
Группа Коксетера	${\overline {Z}}_{3}$ , [6,3,6] ${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Регулярный, квазирегулярный

В области гиперболической геометрии шестиугольная черепичная сотовая структура 6-го порядка является одной из 11 правильных паракомпактных сот в трехмерном гиперболическом пространстве . Он паракомпактный, поскольку имеет ячейки с бесконечным числом граней. Каждая ячейка представляет собой шестиугольную мозаику , вершины которой лежат на орисфере : плоской плоскости в гиперболическом пространстве, приближающейся к единственной идеальной точке на бесконечности.

Символ Шлефли шестиугольных сот — {6,3,6}. Поскольку шестиугольная мозаика плоскости равна {6,3}, эта сот имеет шесть таких шестиугольных мозаик, сходящихся на каждом ребре. Поскольку символ Шлефли треугольной мозаики равен {3,6}, вершинная фигура этой соты представляет собой треугольную мозаику. Таким образом, в каждой вершине этой соты сходится бесконечно много шестиугольных мозаик. ^[1]

Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Связанные мозаики

Сота шестиугольной мозаики порядка 6 аналогична двумерной гиперболической апейрогональной мозаике бесконечного порядка , {∞, ∞}, с бесконечными апейрогональными гранями и со всеми вершинами на идеальной поверхности.

Он содержит и что плитка 2- поверхности гиперцикла , подобная паракомпактным мозаикам и ( усеченная треугольная мозаика бесконечного порядка и апейрогональная мозаика третьего порядка соответственно):

Симметрия

Шестиугольные соты 6-го порядка имеют полусимметричную конструкцию: .

У него также есть подгруппа индекса 6, [6,3 ^*,6], с несимплексной фундаментальной областью. Эта подгруппа соответствует диаграмме Коксетера с шестью ветвями третьего порядка и тремя ветвями бесконечного порядка в форме треугольной призмы: .

Связанные многогранники и соты

Шестиугольные соты 6-го порядка представляют собой обычные гиперболические соты в трехмерном пространстве и одну из одиннадцати паракомпактных сот в трехмерном пространстве.

11 паракомпактных стандартных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

[6,3,6] имеется девять однородных сот В семействе групп Кокстера , включая эту правильную форму.

[6,3,6] семейные соты
{6,3,6}	г {6,3,6}	т{6,3,6}	рр{6,3,6}	т _0,3 {6,3,6}	2т{6,3,6}	тр{6,3,6}	т _0,1,3 {6,3,6}	т _0,1,2,3 {6,3,6}

Эти соты имеют родственные чередующиеся соты, треугольные мозаичные соты , но с более низкой симметрией: ↔ .

Шестиугольные соты мозаики 6-го порядка являются частью последовательности правильных полихор и сот с треугольными фигурами вершин мозаики:

Гиперболические однородные соты : {p,3,6}
Форма	Паракомпакт				Некомпактный
Имя	{3,3,6}	{4,3,6}	{5,3,6}	{6,3,6}	{7,3,6}	{8,3,6}	... {∞,3,6}
Изображение
Клетки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Он также является частью последовательности правильных полихор и сот с шестиугольными ячейками черепицы:

{6,3,p} соты v т и
Space	H³
Form	Paracompact				Noncompact
Name	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	... {6,3,∞}
Coxeter
Image
Vertex figure {3,p}	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Он также является частью последовательности правильных полихор и сот с правильными дельтаэдрическими вершинными фигурами :

{p,3,p} обычные соты
Space	S³	Euclidean E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Ректифицированные соты шестигранной черепицы порядка 6

Ректифицированные соты шестиугольной черепицы порядка 6
Тип	Паракомпактный однородный сотовый
Символы Шлефли	г{6,3,6} или т ₁ {6,3,6}
Диаграммы Кокстера	↔ ↔ ↔ ↔
Клетки	{3,6} г{6,3}
Лица	треугольник {3} шестигранник {6}
Вершинная фигура	шестиугольная призма
Группы Кокстера	${\overline {Z}}_{3}$ , [6,3,6] ${\overline {VP}}_{3}$ , [6,3 ^[3]] ${\overline {PP}}_{3}$ , [3 ^[3,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Выпрямленные соты шестиугольной мозаики порядка 6 , t ₁ {6,3,6}, имеет треугольную мозаику и тригексагональные грани мозаики с шестиугольной призмы фигурой вершины .

его также можно рассматривать как гексагональную мозаику четверти порядка 6 , q{6,3,6}, ↔ .

Это аналогично двумерному гиперболическому апейрогональному мозаике 4-го порядка , r{∞,∞} с бесконечными апейрогональными гранями и со всеми вершинами на идеальной поверхности.

Связанные соты

Шестиугольные соты 6-го порядка являются частью серии сот с шестиугольными призматическими фигурами вершин :

г{р,3,6}
v
т
и
Космос	ЧАС ³
Форма	Паракомпакт				Некомпактный
Имя	г {3,3,6}	г {4,3,6}	г {5,3,6}	г {6,3,6}	г {7,3,6}	... г{∞,3,6}
Изображение
Клетки {3,6}	г{3,3}	г{4,3}	г{5,3}	г{6,3}	г{7,3}	г{∞,3}

Он также является частью матрицы трехмерных четвертных сот: q{2p,4,2q}

Евклидовы /гиперболические ( паракомпактные / некомпактные ) четвертьсоты q{p,3,q}
p \ q	4	6	8	... ∞
4	q{4,3,4} ↔ ↔	q{4,3,6} ↔ ↔	q{4,3,8} ↔	q{4,3,∞} ↔
6	q{6,3,4} ↔ ↔	q{6,3,6} ↔	q{6,3,8} ↔	q{6,3,∞} ↔
8	q{8,3,4} ↔	q{8,3,6} ↔	q{8,3,8} ↔	q{8,3,∞} ↔
... ∞	q{∞,3,4} ↔	q{∞,3,6} ↔	q{∞,3,8} ↔	q{∞,3,∞} ↔

Усеченные шестиугольные соты для черепицы порядка 6

Усеченные шестиугольные соты для черепицы порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т{6,3,6} или т _0,1 {6,3,6}
Диаграмма Кокстера	↔
Клетки	{3,6} т{6,3}
Лица	треугольник {3} двенадцатиугольник {12}
Вершинная фигура	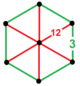шестиугольная пирамида
Группы Кокстера	${\overline {Z}}_{3}$ , [6,3,6] ${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный

Усеченные соты шестиугольной мозаики порядка 6 , t _0,1 {6,3,6}, имеет треугольную мозаику и усеченные шестиугольные грани мозаики с шестиугольной пирамиды фигурой вершины . ^[2]

Усеченные шестиугольные соты порядка 6

Усеченные шестиугольные соты порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	бт{6,3,6} или т _1,2 {6,3,6}
Диаграмма Кокстера	↔
Клетки	т{3,6}
Лица	шестигранник {6}
Вершинная фигура	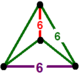тетраэдр
Группы Кокстера	$2\times {\overline {Z}}_{3}$ , [[6,3,6]] ${\overline {VP}}_{3}$ , [6,3 ^[3]] ${\overline {V}}_{3}$ , [3,3,6]
Характеристики	Обычный

Шестиугольные соты 6-го порядка с усеченными битами представляют собой конструкцию с более низкой симметрией обычных шестиугольных сот . ↔ . Он содержит шестиугольные грани мозаики с тетраэдра фигурой вершины .

Соты шестиугольной черепицы со складками порядка 6

Соты шестиугольной черепицы со складками порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	рр{6,3,6} или т _0,2 {6,3,6}
Диаграмма Кокстера	↔
Клетки	г{3,6} рр{6,3} {}x{6}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	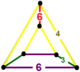клин
Группы Кокстера	${\overline {Z}}_{3}$ , [6,3,6] ${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный

Соты со смещенной шестиугольной мозаикой порядка 6 , t _0,2 {6,3,6}, имеет тригексагональную мозаику , ромбитригексагональную мозаику и ячейки шестиугольной призмы с клина фигурой вершины .

Скошенные шестиугольные соты порядка 6

Скошенные шестиугольные соты порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	тр{6,3,6} или т _0,1,2 {6,3,6}
Диаграмма Кокстера	↔
Клетки	тр{3,6} т{3,6} {}x{6}
Лица	треугольник {3} квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	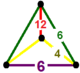зеркальная клиновидная кость
Группы Кокстера	${\overline {Z}}_{3}$ , [6,3,6] ${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный

Скошенные шестиугольные соты 6-го порядка , t _0,1,2 {6,3,6}, имеет шестиугольную мозаику , усеченную тригексагональную мозаику и ячейки шестиугольной призмы с зеркальной фигурой клиновидной вершины .

Шестиугольные соты для черепицы с прорезями порядка 6

Шестиугольные соты для черепицы с прорезями порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т _0,3 {6,3,6}
Диаграмма Кокстера	↔
Клетки	{6,3} {}×{6}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	треугольная антипризма
Группы Кокстера	$2\times {\overline {Z}}_{3}$ , [[6,3,6]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Стертые соты шестиугольной черепицы порядка 6 , t _0,3 {6,3,6}, имеет шестиугольную мозаику и ячейки шестиугольной призмы с антипризмы треугольной фигурой вершины .

Это аналогично двумерной гиперболической ромбогексагексагональной мозаике , rr{6,6}, с квадратными и шестиугольными гранями:

Усеченные шестиугольные соты порядка 6

Усеченные шестиугольные соты порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т _0,1,3 {6,3,6}
Диаграмма Кокстера
Клетки	т{6,3} рр{6,3} {}x{6} {}х{12}
Лица	треугольник {3} квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	равнобедренно-трапециевидная пирамида
Группы Кокстера	${\overline {Z}}_{3}$ , [6,3,6]
Характеристики	Вершинно-транзитивный

Усеченные соты шестиугольной черепицы порядка 6 , t _0,1,3 {6,3,6}, имеет усеченную шестиугольную черепицу , ромбитригексагональную мозаику , шестиугольную призму и ячейки двенадцатиугольной призмы с равнобедренно-трапециевидной пирамиды фигурой вершины .

Всеусеченные шестиугольные соты порядка 6

Всеусеченные шестиугольные соты порядка 6
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т _0,1,2,3 {6,3,6}
Диаграмма Кокстера
Клетки	тр{6,3} {}х{12}
Лица	квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	филлический дисфеноид
Группы Кокстера	$2\times {\overline {Z}}_{3}$ , [[6,3,6]]
Характеристики	Вершинно-транзитивный

Всеусеченные шестиугольные соты 6-го порядка , t _0,1,2,3 {6,3,6}, имеет усеченную тригексагональную мозаику и двенадцатиугольные призматические ячейки с филлической фигурой дисфеноида в вершине .

Шестиугольные соты чередующегося порядка 6

Шестиугольные соты чередующегося порядка 6
Тип	Паракомпактный однородный сотовый
Символы Шлефли	ч{6,3,6}
Диаграммы Кокстера	↔
Клетки	{3,6} {3 ^[3]}
Лица	треугольник {3}
Вершинная фигура	шестиугольная плитка
Группы Кокстера	${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Регулярный, квазирегулярный

представляют Шестиугольные соты чередующегося порядка 6 собой конструкцию с более низкой симметрией обычных треугольных сот . ↔ . Он содержит треугольные грани мозаики в шестиугольной вершине мозаики .

Шестиугольная сотовая плитка Cantic order-6

Шестиугольная сотовая плитка Cantic order-6
Тип	Паракомпактный однородный сотовый
Символы Шлефли	ч ₂ {6,3,6}
Диаграммы Кокстера	↔
Клетки	т{3,6} г{6,3} ч ₂ {6,3}
Лица	треугольник {3} шестигранник {6}
Вершинная фигура	треугольная призма
Группы Кокстера	${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

представляют Шестиугольные соты кантического порядка 6 собой конструкцию с более низкой симметрией выпрямленных треугольных сот мозаики . ↔ , с тригексагональной мозаикой и гранями шестиугольной мозаики в треугольной призмы фигуре вершины .

Шестиугольная плитка Runcic порядка 6 в сотах

Шестиугольная плитка Runcic порядка 6 в сотах
Тип	Паракомпактный однородный сотовый
Символы Шлефли	ч ₃ {6,3,6}
Диаграммы Кокстера	↔
Клетки	рр{3,6} {6,3} {3 ^[3]} {3}х{}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	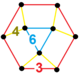треугольный купол
Группы Кокстера	${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный

Руничная шестиугольная черепица-соты , h ₃ {6,3,6}, , или , имеет шестиугольную мозаику , ромбитригексагональную мозаику , треугольную мозаику и треугольные грани призмы , с купола треугольной фигурой вершины .

Шестиугольные соты рунического порядка-6

Шестиугольные соты Runcicantic порядка 6
Тип	Паракомпактный однородный сотовый
Символы Шлефли	ч _2,3 {6,3,6}
Диаграммы Кокстера	↔
Клетки	тр{6,3} т{6,3} ч ₂ {6,3} {}х{3}
Лица	треугольник {3} квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	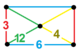прямоугольная пирамида
Группы Кокстера	${\overline {VP}}_{3}$ , [6,3 ^[3]]
Характеристики	Вершинно-транзитивный

, Шестиугольные соты ранцикантического порядка 6 h _2,3 {6,3,6}, , или , содержит усеченную тригексагональную мозаику , усеченную шестиугольную мозаику , тригексагональную мозаику и грани треугольной призмы с прямоугольной пирамиды фигурой вершины .

См. также

Ссылки

^ Коксетер Красота геометрии , 1999, Глава 10, Таблица III
^ Вращение Твиттера вокруг трехкратной оси

Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Правильные соты в гиперболическом пространстве ) Таблица III
Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN 0-8247-0709-5 (Глава 16-17: Геометрии трехмерных многообразий I, II)
Нормана Джонсона Равномерные многогранники , рукопись
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Н. В. Джонсон: Геометрии и преобразования , (2018) Глава 13: Гиперболические группы Кокстера

[1] Коксетер Красота геометрии , 1999, Глава 10, Таблица III

[2] Вращение Твиттера вокруг трехкратной оси

[1]

[2]