Заказ-3-4 Гептагональные соты
| Заказ-3-4 Гептагональные соты | |
|---|---|
| Тип | Регулярные соты |
| Символ Släfli | {7,3,4} |
| Кокситерная диаграмма | |
| Ячейки | {7,3} 
|
| Лица | Heptagon {7} |
| Вершина фигура | Октаэдрон {3,4} |
| Двойной | {4,3,7} |
| Коксетерская группа | [7,3,4] |
| Характеристики | Обычный |
В геометрии гиперболического 3-пространства , HEPT-3-4 Heptagonal Honeycomb или 7,3,4 Honeycomb, регулярная космическая тесселяция (или соты ). Каждая бесконечная клетка состоит из гептагональной плитки, чьи вершины лежат на 2-гиперцикле , каждый из которых имеет ограничивающий круг на идеальной сфере.
Геометрия
[ редактировать ]Символ Schläfli of the Order-3-4 Heptagonal Honeycomb составляет {7,3,4}, с четырьмя гептагональными привязками на каждом краю. Фигура вершины этого соты - октаэдр, {3,4}.
 Модель диска Пуанкаре (центр вершины) |
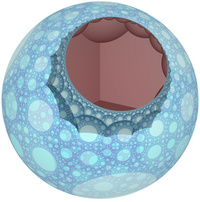 Одна гипердеальная клетка ограничивает круг на идеальной поверхности |
 Идеальная поверхность |
Связанные политопы и соты
[ редактировать ]Это часть серии обычных политопов и соты с символом {P, 3,4} Schläfli и октаэдрическими вершинами: фигуры :
| {p, 3,4} Регулярные соты |
|---|
Заказ-3-4 восьмиугольные соты
[ редактировать ]| Заказ-3-4 восьмиугольные соты | |
|---|---|
| Тип | Регулярные соты |
| Символ Släfli | {8,3,4} |
| Кокситерная диаграмма | |
| Ячейки | {8,3} 
|
| Лица | Octagon {8} |
| Вершина фигура | Октаэдрон {3,4} |
| Двойной | {4,3,8} |
| Коксетерская группа | [8,3,4] [8,3 1,1 ] |
| Характеристики | Обычный |
В геометрии гиперболического 3-пространства в восьмиугольных сотах Order -3-4 или 8,3,4 Honeycomb регулярно наполняет космические тесселяции (или соты ). Каждая бесконечная клетка состоит из восьмиугольной плитки, чьи вершины лежат на 2-гиперциклом , каждый из которых имеет ограничивающий круг на идеальной сфере.
Символ Schläfli- восьмиугольных сотовых сотов {8,3,4}, с четырьмя восьмиугольными уточнениями, встречающимися на каждом краю. Фигура вершины этого соты - октаэдр, {3,4}.
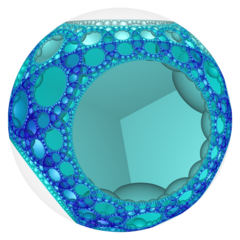 Модель диска Пуанкаре (центр вершины) |
Заказ-3-4 соты выглядят
[ редактировать ]| Заказ-3-4 соты выглядят | |
|---|---|
| Тип | Регулярные соты |
| Символ Släfli | {∞,3,4} |
| Кокситерная диаграмма | |
| Ячейки | {∞,3} 
|
| Лица | Apeirogon {∞} |
| Вершина фигура | Октаэдрон {3,4} |
| Двойной | {4,3,∞} |
| Коксетерская группа | [∞,3,4] [∞,3 1,1 ] |
| Характеристики | Обычный |
В геометрии гиперболического 3-пространства Орден -3-4 Apeironal Honeycomb или ∞, 3,4 соты- регулярное пространство, заполняющее космические тесселяции (или соты ). Каждая бесконечная клетка состоит из апейрогональной плитки Order-3, чьи вершины лежат на 2-гиперцикле , каждый из которых имеет ограниченный круг на идеальной сфере.
Символ Schläfli состоит Apeirogonal Honeycomb Order-3-4 из {∞, 3,4}, с четырьмя порядками-3 apeironal tilings, встречающимися на каждом краю. Фигура вершины этого соты - октаэдр , {3,4}.
 Модель диска Пуанкаре (центр вершины) |
 Идеальная поверхность |
Смотрите также
[ редактировать ]Ссылки
[ редактировать ]- Коксетер , обычные политопы , 3 -й. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: обычные политопы и соты, с. 294–296)
- Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Регулярные соты в гиперболическом пространстве ) Таблица III
- Джеффри Р. недели форма пространства, 2 -е издание ISBN 0-8247-0709-5 (Главы 16–17: Геометрия на трех органах I, II)
- Джордж Максвелл, Сфера упаковки и гиперболические размышления , журнал алгебры 79,78-97 (1982) [1]
- Хао Чен, Жан-Филипп Лаббе, Lorentzian Coxeter Groups и Boyd-Maxwell Ball Packings , (2013) [2]
- Визуализация гиперболических сотовых компаний Arxiv: 1511.02851 Roice Nelson, Henry Segerman (2015)
Внешние ссылки
[ редактировать ]- Джон Бэз , Visual Insights : {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Sult at Infinity (2014/08/14)
- Дэнни Калегари , Кляйнан, инструмент для визуализации кляйнских групп, геометрии и воображения 4 марта 2014 года. [3]






