Двойственность Понтрягина

2 -адические целые числа с выбранными соответствующими символами в их двойственной группе Понтрягина.

В математике двойственность Понтрягина - это двойственность между локально компактными абелевыми группами , которая позволяет обобщить преобразование Фурье на все такие группы, включая группу кругов (мультипликативную группу комплексных чисел по модулю один), конечные абелевы группы (с дискретной топологией ). и аддитивная группа целых чисел (также с дискретной топологией), действительные числа и каждое конечномерное векторное пространство над действительными числами или p -адическое поле .

локально Двойственным по Понтрягину компактной абелевой группе является локально компактная абелева топологическая группа, образованная непрерывными групповыми гомоморфизмами группы в группу окружностей с операцией поточечного умножения и топологией равномерной сходимости на компактах. Теорема о двойственности Понтрягина устанавливает двойственность Понтрягина, утверждая, что любая локально компактная абелева группа естественно изоморфна своей бидуальной группе (двойственной к ней). Теорема обращения Фурье является частным случаем этой теоремы.

Тема названа в честь Льва Понтрягина , который заложил основы теории локально компактных абелевых групп и их двойственности в своих ранних математических работах в 1934 году. Трактовка Понтрягина основывалась на второй счетности групп , компактности или дискретности. Это было улучшено для охвата общих локально компактных абелевых групп Эгбертом ван Кампеном в 1935 году и Андре Вейлем в 1940 году.

Введение

Двойственность Понтрягина помещает в единый контекст ряд наблюдений о функциях на вещественной прямой или на конечных абелевых группах:

• Подходящие регулярные комплекснозначные периодические функции на действительной прямой имеют ряды Фурье , и эти функции можно восстановить из их рядов Фурье;
• Подходящие регулярные комплекснозначные функции на действительной прямой имеют преобразования Фурье, которые также являются функциями на действительной прямой, и, как и периодические функции, эти функции могут быть восстановлены из их преобразований Фурье; и
• Комплекснозначные функции на конечной абелевой группе имеют дискретные преобразования Фурье , которые являются функциями на двойственной группе , которая является (неканонически) изоморфной группой. Более того, любую функцию конечной абелевой группы можно восстановить по ее дискретному преобразованию Фурье.

Теория, введенная Львом Понтрягиным и объединенная с мерой Хаара, введенной Джоном фон Нейманом , Андре Вейлем и другими, зависит от теории дуальной группы к локально компактной абелевой группе.

Это аналогично двойственному векторному пространству векторного пространства: конечномерное векторное пространство $V$ и его двойственное векторное пространство $V^{*}$ не являются естественно изоморфными, но алгебра эндоморфизмов (алгебра матриц) одного изоморфна противоположной алгебре эндоморфизмов другого: ${\text{End}}(V)\cong {{\text{End}}(V^{*})}^{\text{op}},$ через транспонирование. Аналогично, группа $G$ и его двойственная группа ${\widehat {G}}$ в общем случае не изоморфны, но их кольца эндоморфизмов противоположны друг другу: ${\text{End}}(G)\cong {\text{End}}({\widehat {G}})^{\text{op}}$. Если говорить более категорично, то это не просто изоморфизм алгебр эндоморфизмов, а контравариантная эквивалентность категорий – см. § Категорические соображения .

Определение

Дополнительная информация: Локально компактная абелева группа.

Топологическая группа является локально компактной группой, если лежащее в ее основе топологическое пространство локально компактно и хаусдорфово ; топологическая группа абелева, если лежащая в ее основе группа абелева .Примеры локально компактных абелевых групп включают конечные абелевы группы, целые числа (оба для дискретной топологии , которая также индуцируется обычной метрикой), действительные числа, группу окружностей T (обе с их обычной метрической топологией), а также p -адические числа (с их обычной p -адической топологией).

Для локально компактной абелевой группы $G$ является двойственной Понтрягину группа ${\widehat {G}}$ непрерывных гомоморфизмов групп из $G$ в круговую группу $T$. То есть, $${\widehat {G}}:=\operatorname {Hom} (G,T).$$Двойник Понтрягина ${\widehat {G}}$ обычно наделяется топологией , заданной равномерной сходимостью на компактах (т. е. топологией, индуцированной компактно-открытой топологией в пространстве всех непрерывных функций из $G$ к $T$).

Например, $${\widehat {\mathbb {Z} /n\mathbb {Z} }}=\mathbb {Z} /n\mathbb {Z} ,\ {\widehat {\mathbb {Z} }}=T,\ {\widehat {\mathbb {R} }}=\mathbb {R} ,\ {\widehat {T}}=\mathbb {Z} .$$

Теорема двойственности Понтрягина

Теорема — Существует канонический изоморфизм $G\cong {\widehat {\widehat {G}}}$ между любой локально компактной абелевой группой $G$ и его двойной двойной.

Канонический означает, что существует естественно определенное отображение. $\operatorname {ev} _{G}\colon G\to {\widehat {\widehat {G}}}$ ; что еще более важно, карта должна быть функториальной в $G$. Для персонажа $\chi$ группы $G$, канонический изоморфизм $\operatorname {ev} _{G}$ определяется на $x\in G$ следующее: $$\operatorname {ev} _{G}(x)(\chi )=\chi (x)\in \mathbb {T} .$$То есть, $$\operatorname {ev} _{G}(x):(\chi \mapsto \chi (x)).$$

Другими словами, каждый элемент группы $x$ идентифицируется с оценочным персонажем на двойнике. Это сильно аналогично каноническому изоморфизму между конечномерным векторным пространством и его двойным двойственным пространством : $V\cong V^{**}$, и стоит отметить, что любое векторное пространство $V$ является абелевой группой . Если $G$ — конечная абелева группа, то $G\cong {\widehat {G}}$ но этот изоморфизм не каноничен. Чтобы сделать это утверждение точным (в общем), необходимо подумать о дуализации не только групп, но и отображений между группами, чтобы рассматривать дуализацию как функтор и доказать, что тождественный функтор и функтор дуализации не являются естественным образом эквивалентными. Также из теоремы двойственности следует, что для любой группы (не обязательно конечной) функтор дуализации является точным функтором .

Двойственность Понтрягина и преобразование Фурье

Ее мера

Основная статья: Мера Хаара

Один из самых замечательных фактов о локально компактной группе $G$ заключается в том, что оно несет в себе уникальную естественную меру — меру Хаара , которая позволяет последовательно измерять «размер» достаточно регулярных подмножеств множества. $G$. Под «достаточно регулярным подмножеством» здесь понимается борелевское множество ; то есть элемент σ-алгебры, порожденный компактами . Точнее, правая мера Хаара на локально компактной группе. $G$ является счетно-аддитивной мерой µ, определенной на борелевских множествах $G$ который является правоинвариантным в том смысле, что $\mu (Ax)=\mu (A)$ для $x$ элемент $G$ и $A$ подмножество Бореля $G$ а также удовлетворяет некоторым условиям регулярности (подробно изложенным в статье о мере Хаара ). За исключением положительных коэффициентов масштабирования, мера Хаара $G$ является уникальным.

Мера Хаара $G$ позволяет нам определить понятие интеграла для ( комплексных -значных) борелевских функций, определенных на группе. В частности, можно рассмотреть различные L ^п пространства, ассоциированные с мерой Хаара $\mu$. Конкретно, $${\mathcal {L}}_{\mu }^{p}(G)=\left\{(f:G\to \mathbb {C} )\ {\Big |}\ \int _{G}|f(x)|^{p}\ d\mu (x)<\infty \right\}.$$

Заметим, что поскольку любые две меры Хаара на $G$ равны с точностью до масштабного коэффициента, это $L^{p}$-пространство не зависит от выбора меры Хаара и поэтому, возможно, может быть записано как $L^{p}(G)$. Однако $L^{p}$-норма в этом пространстве зависит от выбора меры Хаара, поэтому, если кто-то хочет говорить об изометриях, важно отслеживать используемую меру Хаара.

Преобразование Фурье и формула обращения Фурье для L ¹ -функции

Двойственная группа локально компактной абелевой группы используется в качестве основного пространства для абстрактной версии преобразования Фурье . Если $f\in L^{1}(G)$, то преобразование Фурье — это функция ${\widehat {f}}$ на ${\widehat {G}}$ определяется $${\widehat {f}}(\chi )=\int _{G}f(x){\overline {\chi (x)}}\ d\mu (x),$$где интеграл относится к мере Хаара $\mu$ на $G$. Это также обозначается $({\mathcal {F}}f)(\chi )$. Обратите внимание, что преобразование Фурье зависит от выбора меры Хаара. Нетрудно показать, что преобразование Фурье $L^{1}$ функция включена $G$ является ограниченной непрерывной функцией на ${\widehat {G}}$ который исчезает в бесконечности .

Формула обращения Фурье для $L^{1}$-Функции — для каждой меры Хаара $\mu$ на $G$ существует единственная мера Хаара $\nu$ на ${\widehat {G}}$ такое, что всякий раз, когда $f\in L^{1}(G)$ и ${\widehat {f}}\in L^{1}\left({\widehat {G}}\right)$, у нас есть $$f(x)=\int _{\widehat {G}}{\widehat {f}}(\chi )\chi (x)\ d\nu (\chi )\qquad \mu {\text{-almost everywhere}}$$Если $f$ непрерывно, то это тождество справедливо для всех $x$.

Обратное преобразование Фурье интегрируемой функции на ${\widehat {G}}$ дается $${\check {g}}(x)=\int _{\widehat {G}}g(\chi )\chi (x)\ d\nu (\chi ),$$где интеграл относится к мере Хаара $\nu$ в двойной группе ${\widehat {G}}$. Мера $\nu$ на ${\widehat {G}}$ которая появляется в формуле обращения Фурье, называется двойственной мерой к $\mu$ и может быть обозначен ${\widehat {\mu }}$.

Различные преобразования Фурье можно классифицировать с точки зрения их области определения и области преобразования (группа и двойственная группа) следующим образом (обратите внимание, что $\mathbb {T}$ ) группа кругов :

Трансформировать	Исходный домен, $G$	Преобразование домена, ${\hat {G}}$	Мера, $\mu$
Преобразование Фурье	$\mathbb {R}$	$\mathbb {R}$	${\text{Constant}}\times {\text{Lebesgue measure}}$
ряд Фурье	$\mathbb {T}$	$\mathbb {Z}$	${\text{Constant}}\times {\text{Lebesgue measure}}$
Дискретное преобразование Фурье (DTFT)	$\mathbb {Z}$	$\mathbb {T}$	${\text{Constant}}\times {\text{Counting measure}}$
Дискретное преобразование Фурье (ДПФ)	$\mathbb {Z} _{n}$	$\mathbb {Z} _{n}$	${\text{Constant}}\times {\text{Counting measure}}$

В качестве примера предположим $G=\mathbb {R} ^{n}$, чтобы мы могли подумать о ${\widehat {G}}$ как $\mathbb {R} ^{n}$ по спариванию $(\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }.$ Если $\mu$ является мерой Лебега в евклидовом пространстве, мы получаем обычное преобразование Фурье в $\mathbb {R} ^{n}$ а двойственная мера , необходимая для формулы обращения Фурье, равна ${\widehat {\mu }}=(2\pi )^{-n}\mu$. Если мы хотим получить формулу обращения Фурье с одинаковой мерой с обеих сторон (т. е. поскольку мы можем думать о $\mathbb {R} ^{n}$ как собственное двойное пространство, мы можем попросить ${\widehat {\mu }}$ равняться $\mu$) тогда нам нужно использовать $${\begin{aligned}\mu &=(2\pi )^{-{\frac {n}{2}}}\times {\text{Lebesgue measure}}\\{\widehat {\mu }}&=(2\pi )^{-{\frac {n}{2}}}\times {\text{Lebesgue measure}}\end{aligned}}$$

Однако если мы изменим способ определения $\mathbb {R} ^{n}$ с его двойной группой, используя спаривание $$(\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} },$$тогда мера Лебега на $\mathbb {R} ^{n}$ равна своей собственной двойственной мере . Это соглашение сводит к минимуму количество факторов, $2\pi$ которые появляются в разных местах при вычислении преобразований Фурье или обратных преобразований Фурье в евклидовом пространстве. (Фактически это ограничивает $2\pi$ только в показателе степени, а не в качестве предварительного множителя вне знака интеграла.) Обратите внимание, что выбор способа идентификации $\mathbb {R} ^{n}$ с ее двойственной группой влияет на смысл термина «самодуальная функция», которая представляет собой функцию на $\mathbb {R} ^{n}$ равен собственному преобразованию Фурье: используя классическое спаривание $(\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }$ функция $e^{-{\frac {1}{2}}x^{2}}$ является самодвойственным. Но используя спаривание, которое сохраняет префактор равным единице, $(\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} }$ делает $e^{-\pi x^{2}}$ вместо этого самодвойственный. Это второе определение преобразования Фурье имеет то преимущество, что оно отображает мультипликативную идентичность в идентичность свертки, что полезно как $L^{1}$ является алгеброй свертки. См. следующий раздел о групповой алгебре . Кроме того, эта форма также обязательно изометрична на $L^{2}$ пространства. См. ниже в Plancherel и L. ² Теоремы обращения Фурье .

Групповая алгебра

Основная статья: Групповая алгебра локально компактной группы

Пространство интегрируемых функций на локально компактной абелевой группе $G$ — алгебра , где умножение — это свертка: свертка двух интегрируемых функций $f$ и $g$ определяется как $$(f*g)(x)=\int _{G}f(x-y)g(y)\ d\mu (y).$$

Теорема . Банахово пространство. $L^{1}(G)$ является ассоциативной и коммутативной алгеброй относительно свертки.

Эта алгебра называется групповой алгеброй $G$. По теореме Фубини–Тонелли свертка субмультипликативна относительно $L^{1}$ норма, делая $L^{1}(G)$ алгебра Банахова . Банахова алгебра $L^{1}(G)$ имеет мультипликативный единичный элемент тогда и только тогда, когда $G$ — это дискретная группа, а именно функция, равная 1 в единице и нулю в других местах. Однако в целом он имеет приблизительное тождество : сеть (или обобщенную последовательность) $\{e_{i}\}_{i\in I}$ индексируется по направленному множеству $I$ такой, что $f*e_{i}\to f.$

Преобразование Фурье переводит свертку в умножение, т. е. является гомоморфизмом абелевых банаховых алгебр. $L^{1}(G)\to C_{0}\left({\widehat {G}}\right)$ (нормы ≤ 1): $${\mathcal {F}}(f*g)(\chi )={\mathcal {F}}(f)(\chi )\cdot {\mathcal {F}}(g)(\chi ).$$

В частности, каждому персонажу группы на $G$ соответствует уникальному мультипликативному линейному функционалу на групповой алгебре, определенному формулой $$f\mapsto {\widehat {f}}(\chi ).$$

Важным свойством групповой алгебры является то, что они исчерпывают набор нетривиальных (то есть не тождественно нулевых) мультипликативных линейных функционалов на групповой алгебре; см. раздел 34 ( Loomis 1953 ). Это означает, что преобразование Фурье является частным случаем преобразования Гельфанда .

Планшерель и Л. ² Теоремы обращения Фурье

Как мы уже говорили, двойственная группа к локально компактной абелевой группе сама по себе является локально компактной абелевой группой и, следовательно, имеет меру Хаара или, точнее, целое семейство мер Хаара, связанных с масштабом.

Теорема . Выберите меру Хаара. $\mu$ на $G$ и пусть $\nu$ быть двойной мерой ${\widehat {G}}$ как определено выше. Если $f:G\to \mathbb {C}$ непрерывен с компактным носителем, тогда ${\widehat {f}}\in L^{2}\left({\widehat {G}}\right)$ и $$\int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G}}\left|{\widehat {f}}(\chi )\right|^{2}\ d\nu (\chi ).$$В частности, преобразование Фурье $L^{2}$ изометрия комплекснозначных непрерывных функций компактного носителя на $G$ к $L^{2}$-функции на ${\widehat {G}}$ (используя $L^{2}$-норма относительно $\mu$ для функций на $G$ и $L^{2}$-норма относительно $\nu$ для функций на ${\widehat {G}}$).

Поскольку комплекснозначные непрерывные функции компактного носителя на $G$ являются $L^{2}$-плотный, существует уникальное расширение преобразования Фурье из этого пространства до унитарного оператора $${\mathcal {F}}:L_{\mu }^{2}(G)\to L_{\nu }^{2}\left({\widehat {G}}\right).$$и у нас есть формула $$\forall f\in L^{2}(G):\quad \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G}}\left|{\widehat {f}}(\chi )\right|^{2}\ d\nu (\chi ).$$

Заметим, что для некомпактных локально компактных групп $G$ пространство $L^{1}(G)$ не содержит $L^{2}(G)$, поэтому преобразование Фурье общего $L^{2}$-функции на $G$ «не» задано какой-либо формулой интегрирования (или какой-либо явной формулой). Чтобы определить $L^{2}$ При преобразовании Фурье приходится прибегать к некоторому техническому трюку, например, начинать с плотного подпространства, такого как непрерывные функции с компактным носителем, а затем расширять изометрию путем непрерывности на все пространство. Это унитарное расширение преобразования Фурье — это то, что мы подразумеваем под преобразованием Фурье в пространстве функций, интегрируемых с квадратом.

Дуальная группа также имеет собственное обратное преобразование Фурье; его можно охарактеризовать как обратное (или сопряженное, поскольку оно унитарно) $L^{2}$ Преобразование Фурье. Это содержание $L^{2}$ Формула обращения Фурье следующая.

Теорема . Сопряженным преобразованием Фурье, ограниченным непрерывными функциями с компактным носителем, является обратное преобразование Фурье. $$L_{\nu }^{2}\left({\widehat {G}}\right)\to L_{\mu }^{2}(G)$$где $\nu$ является двойной мерой $\mu$.

В случае $G=\mathbb {T}$ двойная группа ${\widehat {G}}$ естественно изоморфна группе целых чисел $\mathbb {Z}$ а преобразование Фурье специализируется на вычислении коэффициентов рядов Фурье периодических функций.

Если $G$ — конечная группа, мы восстанавливаем дискретное преобразование Фурье . Заметим, что этот случай очень легко доказать непосредственно.

Компактификация Бора и почти-периодичность

Одним из важных применений двойственности Понтрягина является следующая характеристика компактных абелевых топологических групп:

Теорема . Локально компактная абелева группа. $G$ компактна тогда и только тогда, когда дуальная группа ${\widehat {G}}$ является дискретным. Наоборот, $G$ дискретно тогда и только тогда, когда ${\widehat {G}}$ компактен.

Что $G$ компактность подразумевает ${\widehat {G}}$ дискретен или что $G$ дискретность означает, что ${\widehat {G}}$ компактна, является элементарным следствием определения компактно-открытой топологии на ${\widehat {G}}$ и не нуждается в двойственности Понтрягина. Для доказательства обратного используется двойственность Понтрягина.

Компактификация Бора определена для любой топологической группы. $G$, независимо от того, $G$ локально компактна или абелева. Одно из применений двойственности Понтрягина между компактными абелевыми группами и дискретными абелевыми группами состоит в том, чтобы охарактеризовать боровскую компактификацию произвольной абелевой локально компактной топологической группы. Бора Компактификация $B(G)$ из $G$ является ${\widehat {H}}$, где H имеет групповую структуру ${\widehat {G}}$, но с учетом дискретной топологии . Поскольку карта включения $$\iota :H\to {\widehat {G}}$$непрерывен и является гомоморфизмом, двойственный морфизм $$G\sim {\widehat {\widehat {G}}}\to {\widehat {H}}$$ является морфизмом компактной группы, который, как легко показать, удовлетворяет требуемому универсальному свойству .

Смотрите также: почти периодическая функция

Категорические соображения

Двойственность Понтрягина также может быть с пользой рассмотрена функториально . В дальнейшем LCA — категория локально компактных абелевых групп и непрерывных групповых гомоморфизмов. Дуальная групповая конструкция ${\widehat {G}}$ — контравариантный функтор LCA → LCA , представленный (в смысле представимых функторов ) группой окружностей $\mathbb {T}$ как ${\widehat {G}}={\text{Hom}}(G,\mathbb {T} ).$ В частности, двойной двойственный функтор $G\to {\widehat {\widehat {G}}}$ является ковариантным .Категорическая формулировка двойственности Понтрягина затем утверждает, что естественное преобразование между тождественным функтором на LCA и двойным двойственным функтором является изоморфизмом. Если раскрыть понятие естественной трансформации, то это означает, что карты $G\to \operatorname {Hom} (\operatorname {Hom} (G,T),T)$ являются изоморфизмами любой локально компактной абелевой группы $G$, и эти изоморфизмы функториальны в $G$. Этот изоморфизм аналогичен двойному двойственному конечномерному векторному пространству (частный случай для вещественных и комплексных векторных пространств).

Непосредственным следствием этой формулировки является еще одна распространенная категориальная формулировка двойственности Понтрягина: функтор дуальной группы представляет собой эквивалентность категорий от LCA к LCA. ^на .

Двойственность меняет местами подкатегории дискретных групп и компактных групп . Если $R$ это кольцо и $G$ это левый $R$– модуль , двойная группа ${\widehat {G}}$ станет правом $R$–модуль; таким образом мы также можем видеть, что дискретный левый $R$–модули будут двойственны Понтрягину к компактным справа $R$–модули. Кольцо ${\text{End}}(G)$ эндоморфизмов в (измените порядок умножения LCA преобразуется двойственностью в противоположное ему кольцо на другой порядок). Например, если $G$ — бесконечная циклическая дискретная группа, ${\widehat {G}}$ представляет собой круговую группу: первая имеет ${\text{End}}(G)=\mathbb {Z}$ то же самое относится и к последнему.

Обобщения

Обобщения двойственности Понтрягина строятся в двух основных направлениях: для коммутативных топологических групп , не являющихся локально компактными , и для некоммутативных топологических групп. Теории в этих двух случаях очень разные.

Двойственности для коммутативных топологических групп

Когда $G$ является хаусдорфовой абелевой топологической группой, группа ${\widehat {G}}$ с компактно-открытой топологией является хаусдорфовой абелевой топологической группой и естественным отображением из $G$ к его двойственному ${\widehat {\widehat {G}}}$ имеет смысл. Если это отображение является изоморфизмом, то говорят, что $G$ удовлетворяет двойственности Понтрягина (или что $G$ является рефлексивной группой , или рефлексивная группа ). Это было расширено в ряде направлений, помимо случая, когда $G$ локально компактен.

В частности, Сэмюэл Каплан показал в 1948 и 1950 годах, что произвольные произведения и счетные обратные пределы локально компактных (хаусдорфовых) абелевых групп удовлетворяют двойственности Понтрягина. Заметим, что бесконечное произведение локально компактных некомпактных пространств не является локально компактным.

Позже, в 1975 году, Рангачари Венкатараман показал, среди прочего, что каждая открытая подгруппа абелевой топологической группы, удовлетворяющая двойственности Понтрягина, сама удовлетворяет двойственности Понтрягина.

Совсем недавно Серджио Арданса-Тревихано и Мария Хесус Часко. расширили упомянутые выше результаты Каплана. Они показали, что прямые и обратные пределы последовательностей абелевых групп, удовлетворяющих двойственности Понтрягина, также удовлетворяют двойственности Понтрягина, если группы метризуемы или $k_{\omega }$-пространства, но не обязательно локально компактные, если последовательности удовлетворяют некоторым дополнительным условиям.

Однако есть фундаментальный аспект, который изменится, если мы захотим рассматривать двойственность Понтрягина за пределами локально компактного случая. Елена Мартин-Пейнадор доказал в 1995 году, что если $G$ является хаусдорфовой абелевой топологической группой, которая удовлетворяет двойственности Понтрягина и естественному спариванию оценок $${\begin{cases}G\times {\widehat {G}}\to \mathbb {T} \\(x,\chi )\mapsto \chi (x)\end{cases}}$$является (совместно) непрерывным, затем $G$ локально компактен. Как следствие, все нелокально компактные примеры двойственности Понтрягина являются группами, в которых спаривание $G\times {\widehat {G}}\to \mathbb {T}$ не является (совместно) непрерывным.

Другой способ обобщить двойственность Понтрягина на более широкие классы коммутативных топологических групп — это наделить двойственную группу ${\widehat {G}}$ с немного другой топологией, а именно топологией равномерной сходимости на вполне ограниченных множествах . Группы, удовлетворяющие тождеству $G\cong {\widehat {\widehat {G}}}$ при этом предположении называются стереотипными группами . Этот класс также очень широк (и содержит локально компактные абелевы группы), но уже, чем класс рефлексивных групп.

Двойственность Понтрягина для топологических векторных пространств

В 1952 году Марианна Ф. Смит. заметил, что банаховы пространства и рефлексивные пространства , рассматриваемые как топологические группы (с аддитивной групповой операцией), удовлетворяют двойственности Понтрягина. Позже Б.С. Брудовский, Уильям К. Уотерхаус и К. Браунер показал, что этот результат может быть распространен на класс всех квазиполных бочечных пространств (в частности, на все пространства Фреше ). В 1990-е годы Сергей Акбаров дал описание класса топологических векторных пространств, удовлетворяющих более сильному свойству, чем классическая рефлексивность Понтрягина, а именно тождеству $$(X^{\star })^{\star }\cong X$$ где $X^{\star }$ означает пространство всех линейных непрерывных функционалов $f\colon X\to \mathbb {C}$ наделенный топологией равномерной сходимости на вполне ограниченных множествах в $X$ (и $(X^{\star })^{\star }$ означает двойственное к $X^{\star }$ в том же смысле). Пространства этого класса называются пространствами стереотипов , и соответствующая теория нашла ряд приложений в функциональном анализе и геометрии, включая обобщение двойственности Понтрягина для некоммутативных топологических групп.

Двойственности для некоммутативных топологических групп

Для некоммутативных локально компактных групп $G$ классическая конструкция Понтрягина перестает работать по разным причинам, в частности, потому, что персонажи не всегда разделяют точки зрения. $G$, и неприводимые представления $G$ не всегда одномерны. В то же время неясно, как ввести умножение на множестве неприводимых унитарных представлений $G$, и даже не ясно, подойдет ли этот набор на роль двойственного объекта для $G$. Так что проблема построения двойственности в данной ситуации требует полного переосмысления.

Построенные к настоящему времени теории делятся на две основные группы: теории, в которых дуальный объект имеет ту же природу, что и исходный (как в самой дуальности Понтрягина), и теории, в которых исходный объект и его двойственный объект столь радикально отличаются друг от друга. что их нельзя считать объектами одного класса.

Теории второго типа исторически были первыми: вскоре после работы Понтрягина Тадао Таннака (1938) и Марк Крейн (1949) построили теорию двойственности для произвольных компактных групп, известную сейчас как двойственность Таннаки–Крейна . В этой теории двойственный объект для группы $G$ это не группа, а категория ее представлений $\Pi (G)$.

Двойственность для конечных групп.

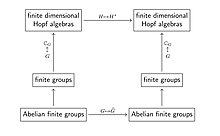
Теории первого типа появились позже, и ключевым примером для них была теория двойственности конечных групп. В этой теории категория конечных групп вкладывается операцией $G\mapsto \mathbb {C} _{G}$ изучения групповой алгебры $\mathbb {C} _{G}$ (над $\mathbb {C}$) в категорию конечномерных алгебр Хопфа , так что функтор двойственности Понтрягина $G\mapsto {\widehat {G}}$ превращается в операцию $H\mapsto H^{*}$ взятия двойственного векторного пространства (которое является функтором двойственности в категории конечномерных алгебр Хопфа).

В 1973 году Леонид Вайнерман , Джордж Кац , Мишель Инок и Жан-Мари Шварц построили общую теорию этого типа для всех локально компактных групп. С 1980-х годов исследования в этой области возобновились после открытия квантовых групп , на которые стали активно переносить построенные теории. Эти теории сформулированы на языке С*-алгебр , или алгебр фон Неймана , и одним из ее вариантов является недавняя теория локально компактных квантовых групп .

Однако одним из недостатков этих общих теорий является то, что в них объекты, обобщающие понятие группы, не являются алгебрами Хопфа в обычном алгебраическом смысле. Этот недостаток можно исправить (для некоторых классов групп) в рамках теорий двойственности, построенных на основе понятия оболочки топологической алгебры.

См. также

• Теорема Питера – Вейля
• Двойственность Картье
• Стереотипное пространство

Ссылки

• Акбаров, С.С. (2003). «Двойственность Понтрягина в теории топологических векторных пространств и в топологической алгебре» . Журнал математических наук . 113 (2): 179–349. дои : 10.1023/А:1020929201133 . S2CID   115297067 .
• Акбаров Сергей С.; Шавгулидзе, Евгений Т. (2003). «О двух классах рефлексивных по Понтрягину пространств» . Математический сборник . 194 (10): 3–26.
• Акбаров, Сергей С. (2009). «Голоморфные функции экспоненциального типа и двойственности для групп Штейна с алгебраической связной составляющей единицы». Журнал математических наук . 162 (4): 459–586. arXiv : 0806.3205 . дои : 10.1007/s10958-009-9646-1 . S2CID   115153766 .
• Акбаров, Сергей С. (2017a). «Непрерывные и гладкие оболочки топологических алгебр. Часть 1». Журнал математических наук . 227 (5): 531–668. arXiv : 1303.2424 . дои : 10.1007/s10958-017-3599-6 . МР   3790317 . S2CID   126018582 .
• Акбаров, Сергей С. (2017b). «Непрерывные и гладкие оболочки топологических алгебр. Часть 2». Журнал математических наук . 227 (6): 669–789. arXiv : 1303.2424 . дои : 10.1007/s10958-017-3600-4 . МР   3796205 . S2CID   128246373 .
• Браунер, Кальман (1973). «Двойственные пространства Фреше и обобщение теоремы Банаха – Дьедонне». Математический журнал Дьюка . 40 (4): 845–855. дои : 10.1215/S0012-7094-73-04078-7 .
• Брудовский, Б.С. (1967). «О k- и c-рефлексивности локально выпуклых векторных пространств» . Литовский математический журнал . 7 (1): 17–21. дои : 10.15388/LMJ.1967.19927 .
• Диксмье, Жак (1969). C*-алгебры и их представления . Готье-Виллар. ISBN  978-2-87647-013-2 .
• Энок, Мишель; Шварц, Жан-Мари (1992). Алгебры Каца и двойственность локально компактных групп . С предисловием Алена Конна. С постфейсом Адриана Окняну. Берлин: Springer-Verlag. дои : 10.1007/978-3-662-02813-1 . ISBN  978-3-540-54745-7 . МР   1215933 .
• Хьюитт, Эдвин; Росс, Кеннет А. (1963). Абстрактный гармонический анализ. Том I: Структура топологических групп. Теория интеграции, представления групп . Основные положения математических наук. Том 115. Берлин-Геттинген-Гейдельберг: Springer-Verlag. ISBN  978-0-387-94190-5 . МР   0156915 .
• Хьюитт, Эдвин; Росс, Кеннет А. (1970). Абстрактный гармонический анализ . Том. 2. Спрингер. ISBN  978-3-662-24595-8 . МР   0262773 .
• Кириллов, Александр А. (1976) [1972]. Элементы теории представлений . Основные принципы математических наук. Том 220. Берлин, Нью-Йорк: Springer-Verlag . ISBN  978-0-387-07476-4 . МР   0412321 .
• Лумис, Линн Х. (1953). Введение в абстрактный гармонический анализ . компании Д. ван Ностранда ISBN  978-0486481234 .
• Моррис, Ю.А. (1977). Двойственность Понтрягина и строение локально компактных абелевых групп . Издательство Кембриджского университета . ISBN  978-0521215435 .
• Онищик, А.Л. (1984), «Двойственность Понтрягина» , Энциклопедия математики , 4 : 481–482, ISBN  978-1402006098
• Райтер, Ганс (1968). Классический гармонический анализ и локально компактные группы . Кларендон Пресс. ISBN  978-0198511892 .
• Рудин, Вальтер (1962). Анализ Фурье на группах . компании Д. ван Ностранда ISBN  978-0471523642 .
• Тиммерманн, Т. (2008). Приглашение к квантовым группам и двойственности - от алгебр Хопфа к мультипликативным унитариям и не только . Учебники EMS по математике, Европейское математическое общество. ISBN  978-3-03719-043-2 .
• Кустерманс, Дж.; Ваес, С. (2000). «Локально компактные квантовые группы» . Научные анналы Высшей нормальной школы . 33 (6): 837–934. дои : 10.1016/s0012-9593(00)01055-7 .
• Арданса-Тревихано, Серджио; Часко, Мария Хесус (2005). «Двойственность Понтрягина последовательных пределов топологических абелевых групп». Журнал чистой и прикладной алгебры . 202 (1–3): 11–21. дои : 10.1016/j.jpaa.2005.02.006 . hdl : 10171/1586 . МР   2163398 .
• Часко, Мария Хесус; Дикранжан, Дикран; Мартин-Пейнадор, Елена (2012). «Обзор рефлексивности абелевых топологических групп» . Топология и ее приложения . 159 (9): 2290–2309. дои : 10.1016/j.topol.2012.04.012 . МР   2921819 .
• Каплан, Сэмюэл (1948). «Расширения двойственности Понтрягина. Часть I: бесконечные произведения». Математический журнал Дьюка . 15 : 649–658. дои : 10.1215/S0012-7094-48-01557-9 . МР   0026999 .
• Каплан, Сэмюэл (1950). «Расширения двойственности Понтрягина. Часть II: прямые и обратные пределы». Математический журнал Дьюка . 17 : 419–435. дои : 10.1215/S0012-7094-50-01737-6 . МР   0049906 .
• Венкатараман, Рангачари (1975). «Расширения дуальности Понтрягина». Математический журнал . 143 (2): 105–112. дои : 10.1007/BF01187051 . S2CID   123627326 .
• Мартин-Пейнадор, Елена (1995). «Рефлексивная допустимая топологическая группа должна быть локально компактной». Труды Американского математического общества . 123 (11): 3563–3566. дои : 10.2307/2161108 . hdl : 10338.dmlcz/127641 . JSTOR   2161108 .
• Редер, Дэвид В. (1974). «Теория категорий в применении к двойственности Понтрягина» . Тихоокеанский математический журнал . 52 (2): 519–527. дои : 10.2140/pjm.1974.52.519 .
• Смит, Марианна Ф. (1952). «Теорема двойственности Понтрягина в линейных пространствах». Анналы математики . 56 (2): 248–253. дои : 10.2307/1969798 . JSTOR   1969798 . МР   0049479 .
• Уотерхаус, Уильям К. (1968). «Двойственные группы векторных пространств» . Тихоокеанский математический журнал . 26 (1): 193–196. дои : 10.2140/pjm.1968.26.193 .