Законы диффузии Фика

О технике измерения сердечного выброса см. Принцип Фика .

Молекулярная диффузия с микроскопической и макроскопической точки зрения. Первоначально на левой стороне барьера (фиолетовая линия) есть молекулы растворенного вещества , а справа нет. Барьер удаляется, и растворенное вещество диффундирует, заполняя весь контейнер. Вверху : одна молекула движется хаотично. Середина : при большем количестве молекул наблюдается четкая тенденция к тому, что растворенное вещество заполняет контейнер все более и более равномерно. Внизу : при огромном количестве молекул растворенного вещества случайность становится необнаружимой: кажется, что растворенное вещество плавно и систематически перемещается из областей с высокой концентрацией в области с низкой концентрацией. Это плавное течение описывается законами Фика.

Законы диффузии Фика описывают диффузию и были впервые сформулированы Адольфом Фиком в 1855 году на основе преимущественно экспериментальных результатов. Их можно использовать для определения диффузии коэффициента D . Первый закон Фика можно использовать для вывода второго закона, который, в свою очередь, идентичен уравнению диффузии .

Первый закон Фика : движение частиц от высокой концентрации к низкой (диффузионный поток) прямо пропорционально градиенту концентрации частиц.

Второй закон Фика : предсказание изменения градиента концентрации со временем из-за диффузии.

Процесс диффузии, подчиняющийся законам Фика, называется нормальной или фиковской диффузией; в противном случае это называется аномальной диффузией или нефиковской диффузией.

История

Впервые об этом сообщил физиолог Адольф Фик в 1855 году. его теперь хорошо известные законы, управляющие переносом массы диффузионным путем. Работа Фика была вдохновлена ​​более ранними экспериментами Томаса Грэма , которые не смогли предложить фундаментальные законы, благодаря которым Фик прославился. Закон Фика аналогичен закономерностям, открытым в ту же эпоху другими выдающимися учеными: закону Дарси (гидравлический поток), закону Ома (перенос заряда) и закону Фурье (перенос тепла).

Эксперименты Фика (по образцу Грэма) касались измерения концентрации и потоков соли, диффундирующей между двумя резервуарами через трубки с водой. Примечательно, что работа Фика в первую очередь касалась диффузии в жидкостях, поскольку в то время диффузия в твердых телах вообще не считалась возможной. Сегодня законы Фика составляют основу нашего понимания диффузии в твердых телах, жидкостях и газах (при отсутствии движения объемной жидкости в последних двух случаях). Когда процесс диффузии не подчиняется законам Фика (что происходит, среди прочего, в случаях диффузии через пористые среды и диффузии набухающих пенетрантов), его называют нефикианским .

Первый закон Фика

Первый закон Фика связывает диффузионный поток с градиентом концентрации. Он постулирует, что поток идет из областей с высокой концентрацией в области с низкой концентрацией, с величиной, которая пропорциональна градиенту концентрации (пространственная производная), или, проще говоря, концепция, согласно которой растворенное вещество будет перемещаться из области с высокой концентрацией в область с высокой концентрацией. область низкой концентрации поперек градиента концентрации. В одном (пространственном) измерении закон может быть записан в различных формах, причем наиболее распространенной формой (см. ) находится в молярной основе:

$J=-D{\frac {d\varphi }{dx}}$

где

• J — диффузионный поток которого , размерность — количество вещества на единицу площади в единицу времени. J измеряет количество вещества, которое пройдет через единицу площади за единицу времени.
• D — коэффициент диффузии или коэффициент диффузии . Его размерность — площадь в единицу времени.
• ${\frac {d\varphi }{dx}}$ градиент концентрации
• φ (для идеальных смесей) — концентрация, имеющая размерность количества вещества в единице объема.
• x — позиция, размерность которой — длина.

D пропорционален квадрату скорости диффундирующих частиц, который зависит от температуры, вязкости жидкости и размера частиц согласно соотношению Стокса-Эйнштейна . В разбавленных водных растворах коэффициенты диффузии большинства ионов близки и имеют значения, которые при комнатной температуре находятся в диапазоне (0,6–2) × 10. ⁻⁹ м ² /с . Для биологических молекул коэффициенты диффузии обычно находятся в диапазоне от 10 ⁻¹⁰ до 10 ⁻¹¹ м ² /с.

В двух или более измерениях мы должны использовать ∇ , оператор del или градиента , который обобщает первую производную, получая

$\mathbf {J} =-D\nabla \varphi$

где J обозначает вектор диффузионного потока.

Движущей силой одномерной диффузии является величина — ⁠ ∂ φ / ∂ x ⁠ , что для идеальных смесей является градиентом концентрации.

Варианты первого закона

Другая форма первого закона — записать его с основной переменной как массовая доля ( y _i , заданная, например, в кг/кг), тогда уравнение изменится на:

$\mathbf {J} _{i}=-{\frac {\rho D}{M_{i}}}\nabla y_{i}$

где

• индекс i обозначает i- й вид,
• J _i — вектор диффузионного потока го i- вещества (например, в моль/м ² -с),
• Mi _— молярная масса го вида i- , а
• ρ смеси — плотность (например, в кг/м ³ ).

The $\rho$ находится вне оператора градиента . Это потому, что:

$y_{i}={\frac {\rho _{si}}{\rho }}$

где ρ _si — парциальная плотность i- го вида.

Помимо этого, в химических системах, отличных от идеальных растворов или смесей, движущей силой диффузии каждого вида является градиент химического потенциала этого вида. Тогда первый закон Фика (одномерный случай) можно записать

$J_{i}=-{\frac {Dc_{i}}{RT}}{\frac {\partial \mu _{i}}{\partial x}}$

где

• индекс i обозначает i- й вид
• c — концентрация (моль/м ³ )
• R — универсальная газовая постоянная (Дж/К/моль).
• T — абсолютная температура (К)
• μ — химический потенциал (Дж/моль).

Движущую силу закона Фика можно выразить как разность летучести :

$J_{i}=-{\frac {D}{RT}}{\frac {\partial f_{i}}{\partial x}}$

Летучесть $f_{i}$ имеет единицы Па. $f_{i}$ - парциальное давление компонента i в паре $f_{i}^{\text{G}}$ или жидкость $f_{i}^{\text{L}}$ фаза. При равновесии пар-жидкость поток испарения равен нулю, поскольку $f_{i}^{\text{G}}=f_{i}^{\text{L}}$.

Вывод первого закона Фика для газов.

Ниже приведены четыре варианта закона Фика для бинарных газовых смесей. Они предполагают: термодиффузия незначительна; объемная сила на единицу массы одинакова у обоих видов; и либо давление постоянно, либо оба вещества имеют одинаковую молярную массу. В этих условиях см. подробно показано, как уравнение диффузии из кинетической теории газов сводится к этой версии закона Фика: $$\mathbf {V_{i}} =-D\nabla \ln y_{i},$$где V _i — скорость диффузии вида i . С точки зрения потока видов это $$\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla y_{i}.$$

Если, кроме того, $\nabla \rho =0$, это сводится к наиболее распространенной форме закона Фика: $$\mathbf {J_{i}} =-D\nabla \varphi .$$

Если (вместо или в дополнение к $\nabla \rho =0$) оба вида имеют одинаковую молярную массу, закон Фика принимает вид $$\mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla x_{i},$$где $x_{i}$ — мольная доля вида i .

Второй закон Фика

Второй закон Фика предсказывает, как диффузия вызывает изменение концентрации во времени. Это уравнение в частных производных , которое в одном измерении гласит:

${\frac {\partial \varphi }{\partial t}}=D\,{\frac {\partial ^{2}\varphi }{\partial x^{2}}}$

где

• φ — концентрация в размерах $[{\mathsf {N}}{\mathsf {L}}^{-3}]$, пример моль/м ³ ; φ = φ ( x , t ) — функция, которая зависит от местоположения x и времени t
• t — время, пример с
• D – коэффициент диффузии в размерах $[{\mathsf {L}}^{2}{\mathsf {T}}^{-1}]$, пример м ² /с
• x — позиция, пример m

В двух или более измерениях мы должны использовать лапласиан Δ = ∇ ² , которое обобщает вторую производную, получая уравнение

${\frac {\partial \varphi }{\partial t}}=D\Delta \varphi$

Второй закон Фика имеет ту же математическую форму, что и уравнение теплопроводности , и его фундаментальное решение такое же, как и ядро ​​теплопроводности , за исключением переключения теплопроводности. $k$ с коэффициентом диффузии $D$: $$\varphi (x,t)={\frac {1}{\sqrt {4\pi Dt}}}\exp \left(-{\frac {x^{2}}{4Dt}}\right).$$

Вывод второго закона Фика.

Второй закон Фика можно вывести из первого закона Фика и закона сохранения массы в отсутствие каких-либо химических реакций:

${\frac {\partial \varphi }{\partial t}}+{\frac {\partial }{\partial x}}J=0\Rightarrow {\frac {\partial \varphi }{\partial t}}-{\frac {\partial }{\partial x}}\left(D{\frac {\partial }{\partial x}}\varphi \right)\,=0$

Полагая коэффициент диффузии D постоянным, можно поменять местами порядки дифференцирования и умножить на константу:

${\frac {\partial }{\partial x}}\left(D{\frac {\partial }{\partial x}}\varphi \right)=D{\frac {\partial }{\partial x}}{\frac {\partial }{\partial x}}\varphi =D{\frac {\partial ^{2}\varphi }{\partial x^{2}}}$

и, таким образом, примут вид уравнений Фика, как указано выше.

Для случая диффузии в двух или более измерениях второй закон Фика принимает вид

${\frac {\partial \varphi }{\partial t}}=D\,\nabla ^{2}\varphi ,$

что аналогично уравнению теплопроводности .

Если коэффициент диффузии не является константой, а зависит от координаты или концентрации, второй закон Фика дает

${\frac {\partial \varphi }{\partial t}}=\nabla \cdot (D\,\nabla \varphi ).$

Важным примером является случай, когда φ находится в устойчивом состоянии, т.е. концентрация не меняется со временем, так что левая часть приведенного выше уравнения равна тождественному нулю. В одном измерении с постоянной D решение для концентрации будет линейным изменением концентрации вдоль x . В двух или более измерениях мы получаем

$\nabla ^{2}\varphi =0,$

которое представляет собой уравнение Лапласа , решения которого математики называют гармоническими функциями .

Примеры решений и обобщение

Второй закон Фика представляет собой частный случай уравнения конвекции-диффузии , в котором нет ни адвективного потока , ни чистого объемного источника. Его можно получить из уравнения непрерывности :

${\frac {\partial \varphi }{\partial t}}+\nabla \cdot \mathbf {j} =R,$

где j — общий поток , а R — чистый объемный источник для φ . Предполагается, что единственным источником потока в этой ситуации является диффузионный поток :

$\mathbf {j} _{\text{diffusion}}=-D\nabla \varphi$

Подключая определение диффузионного потока к уравнению непрерывности и предполагая отсутствие источника ( R = 0 ), мы приходим ко второму закону Фика:

${\frac {\partial \varphi }{\partial t}}=D{\frac {\partial ^{2}\varphi }{\partial x^{2}}}$

Если бы поток был результатом как диффузионного потока, так и адвективного потока , уравнение конвекции-диффузии результатом было бы .

Пример решения 1: источник постоянной концентрации и длина диффузии

Простой случай диффузии со временем t в одном измерении (взятом за ось x ) от границы, расположенной в положении x = 0 , где концентрация поддерживается на уровне n ₀ :

$n\left(x,t\right)=n_{0}\operatorname {erfc} \left({\frac {x}{2{\sqrt {Dt}}}}\right).$

где erfc — дополнительная функция ошибок . Это тот случай, когда коррозионные газы диффундируют через окислительный слой к поверхности металла (если предположить, что концентрация газов в среде постоянна, а диффузионное пространство – то есть слой продуктов коррозии – полубесконечно , начиная с 0 на поверхности и распространяется бесконечно глубоко в материале). Если, в свою очередь, диффузионное пространство бесконечно (проходит как через слой с n ( x , 0) = 0 , x > 0 , так и через слой с n ( x , 0) = n ₀ , x ≤ 0 ), то решение дополняется только коэффициентом ⁠ 1/2 . ( ⁠ перед n ₀ так как диффузия теперь происходит в обоих направлениях) Этот случай справедлив, когда некоторый раствор с концентрацией n = ₀ контактирует со слоем чистого растворителя. (Бокштейн, 2005) Длина 2 √ Dt называется диффузионной длиной и является мерой того, насколько далеко концентрация распространилась в направлении x за счет диффузии за время t (Bird, 1976).

В качестве быстрого приближения функции ошибок первые два члена ряда Тейлора можно использовать :

$n(x,t)=n_{0}\left[1-2\left({\frac {x}{2{\sqrt {Dt\pi }}}}\right)\right]$

Если D зависит от времени, длина диффузии становится

$2{\sqrt {\int _{0}^{t}D(\tau )\,d\tau }}.$

Эта идея полезна для оценки длины диффузии в цикле нагрева и охлаждения, где D меняется в зависимости от температуры.

Пример решения 2: Броуновская частица и среднеквадратичное смещение

Другой простой случай диффузии — броуновское движение одной частицы. частицы Среднеквадратичное смещение от исходного положения равно: $${\text{MSD}}\equiv \langle (\mathbf {x} -\mathbf {x_{0}} )^{2}\rangle =2nDt$$где $n$ - размерность броуновского движения частицы. Например, диффузия молекулы через клеточную мембрану толщиной 8 нм является одномерной диффузией из-за сферической симметрии; Однако диффузия молекулы от мембраны к центру эукариотической клетки представляет собой трехмерную диффузию. Для цилиндрического кактуса диффузия от фотосинтезирующих клеток на его поверхности к его центру (оси его цилиндрической симметрии) является двумерной диффузией.

Квадратный корень из MSD, ${\sqrt {2nDt}}$, часто используется как характеристика того, насколько далеко частица переместилась с течением времени. $t$ истекло. MSD симметрично распределен в 1D, 2D и 3D пространстве. Таким образом, распределение вероятностей величины MSD в 1D является гауссовым, а в 3D — распределением Максвелла-Больцмана.

Обобщения

• В неоднородных средах коэффициент диффузии меняется в пространстве D = D ( x ) . Эта зависимость не влияет на первый закон Фика, но меняется второй закон: $${\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=D(x)\Delta \varphi (x,t)+\sum _{i=1}^{3}{\frac {\partial D(x)}{\partial x_{i}}}{\frac {\partial \varphi (x,t)}{\partial x_{i}}}$$
• В анизотропных средах коэффициент диффузии зависит от направления. Это симметричный тензор D _ji = D _ij . Первый закон Фика меняется на $$J=-D\nabla \varphi ,$$ это произведение тензора и вектора: $$J_{i}=-\sum _{j=1}^{3}D_{ij}{\frac {\partial \varphi }{\partial x_{j}}}.$$ Для уравнения диффузии эта формула дает $${\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D\nabla \varphi (x,t){\bigr )}=\sum _{i=1}^{3}\sum _{j=1}^{3}D_{ij}{\frac {\partial ^{2}\varphi (x,t)}{\partial x_{i}\partial x_{j}}}.$$ Симметричная матрица коэффициентов диффузии D _ij должна быть положительно определенной . Это необходимо для того, чтобы правый оператор стал эллиптическим .
• Для неоднородных анизотропных сред эти две формы уравнения диффузии следует объединить в $${\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=\sum _{i,j=1}^{3}\left(D_{ij}(x){\frac {\partial ^{2}\varphi (x,t)}{\partial x_{i}\partial x_{j}}}+{\frac {\partial D_{ij}(x)}{\partial x_{i}}}{\frac {\partial \varphi (x,t)}{\partial x_{i}}}\right).$$
• Подход, основанный на подвижности Эйнштейна и формуле Теорелла, дает следующее обобщение уравнения Фика для многокомпонентной диффузии идеальных компонентов: $${\frac {\partial \varphi _{i}}{\partial t}}=\sum _{j}\nabla \cdot \left(D_{ij}{\frac {\varphi _{i}}{\varphi _{j}}}\nabla \,\varphi _{j}\right).$$ где φ _i — концентрации компонентов, а D _ij — матрица коэффициентов. Здесь индексы i и j относятся к различным компонентам, а не к пространственным координатам.

Точно такие же члены входят в формулы Чепмена –Энскога для диффузии в газах . Эти физические модели диффузии отличаются от тестовых моделей ∂ _t φ _i = Σ _j D _ij Δ φ _j , которые справедливы для очень малых отклонений от равномерного равновесия. Ранее такие члены были введены в уравнение диффузии Максвелла–Стефана .

анизотропных коэффициентов многокомпонентной диффузии нужен тензор четвертого ранга, например Dij _{Для , αβ} , где i , j относятся к компонентам, а α , β = 1, 2, 3 соответствуют пространственным координатам.

Приложения

Уравнения, основанные на законе Фика, обычно используются для моделирования транспортных процессов в пищевых продуктах, нейронах , биополимерах , фармацевтических препаратах , пористых почвах , динамике населения , ядерных материалах, физике плазмы и процессах легирования полупроводников . Теория вольтамперометрических методов основана на решениях уравнения Фика. С другой стороны, в некоторых случаях «фикиан» (другое распространенное приближение уравнения переноса - это приближение теории диффузии) «Описание недостаточно. Например, в науке о полимерах и пищевой промышленности требуется более общий подход для описания переноса компонентов в материалах, подвергающихся стеклованию . Еще одна общая основа - это диффузии Максвелла – Стефана. уравнения многокомпонентного массопереноса , из которого можно получить закон Фика как предельный случай, когда смесь чрезвычайно разбавлена ​​и каждая химическая частица взаимодействует только с основной смесью, а не с другими частицами. Для учета присутствия нескольких веществ в неразбавленной смеси используются несколько вариантов уравнений Максвелла-Стефана. См. также недиагональные связанные транспортные процессы ( Онзагера отношения ).

Течение Фика в жидкостях

Когда две смешивающиеся жидкости приводятся в контакт и происходит диффузия, макроскопическая (или средняя) концентрация развивается по закону Фика. В мезоскопическом масштабе, то есть между макроскопическим масштабом, описываемым законом Фика, и молекулярным масштабом, где имеют место молекулярные случайные блуждания , флуктуациями пренебрегать нельзя. Такие ситуации можно успешно смоделировать с помощью флуктуационной гидродинамики Ландау-Лифшица. В этой теоретической структуре диффузия обусловлена ​​флуктуациями, размеры которых варьируются от молекулярного до макроскопического масштаба.

В частности, флуктуационные гидродинамические уравнения включают член потока Фика с заданным коэффициентом диффузии, а также уравнения гидродинамики и стохастические члены, описывающие флуктуации. При расчете флуктуаций пертурбативным подходом приближением нулевого порядка является закон Фика. Первый порядок дает флуктуации, и получается, что флуктуации способствуют диффузии. Это представляет собой в некотором роде тавтологию , поскольку явления, описываемые низшим приближением, являются результатом более высокого приближения: эта проблема решается только путем перенормировки уравнений флуктуационной гидродинамики.

Скорость сорбции и частота столкновений разбавленного растворенного вещества

Адсорбция, абсорбция и столкновение молекул, частиц и поверхностей являются важными проблемами во многих областях. Эти фундаментальные процессы регулируют химические, биологические реакции и реакции окружающей среды. Их скорость можно рассчитать, используя константу диффузии и законы диффузии Фика, особенно когда эти взаимодействия происходят в разбавленных растворах.

Обычно константу диффузии молекул и частиц, определенную уравнением Фика, можно рассчитать с помощью уравнения Стокса-Эйнштейна . В сверхкоротком времени, порядка времени диффузии a ² / D , где a — радиус частицы, диффузия описывается уравнением Ланжевена . При более длительном времени уравнение Ланжевена переходит в уравнение Стокса–Эйнштейна . Последнее подходит для условий разбавленного раствора, когда рассматривается дальняя диффузия. Согласно теореме о флуктуации-диссипации, основанной на уравнении Ланжевена, в долгосрочном пределе и когда частица значительно плотнее окружающей жидкости, константа диффузии, зависящая от времени, равна:

$D(t)=\mu \,k_{\rm {B}}T\left(1-e^{-t/(m\mu )}\right)$

где (все в единицах СИ)

• k _B — постоянная Больцмана
• Т — абсолютная температура
• μ — подвижность частицы в жидкости или газе, которую можно рассчитать с помощью соотношения Эйнштейна (кинетическая теория)
• m - масса частицы
• т это время.

Для одной молекулы, такой как органические молекулы или биомолекулы (например, белки) в воде, экспоненциальный член пренебрежимо мал из-за небольшого произведения mμ в сверхбыстрой пикосекундной области, что не имеет отношения к относительно более медленной адсорбции разбавленного растворенного вещества.

Схема молекулярной диффузии в растворе. Оранжевые точки — это молекулы растворенного вещества, молекулы растворителя не нарисованы, черная стрелка — пример траектории случайного блуждания, а красная кривая — функция вероятности диффузионного гауссовского уширения из закона диффузии Фика. ^{:Инжир. 9}

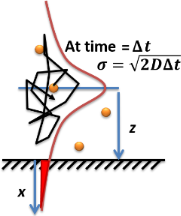
Скорость адсорбции или абсорбции разбавленного растворенного вещества на поверхности или границе раздела в растворе (газе или жидкости) можно рассчитать с использованием законов диффузии Фика. Накопленное количество молекул, адсорбированных на поверхности, выражается уравнением Ленгмюра-Шефера путем интегрирования уравнения диффузионного потока во времени, как показано в моделируемой молекулярной диффузии в первом разделе этой страницы:

$\Gamma =2AC_{b}{\sqrt {\frac {Dt}{\pi }}}$

• A — площадь поверхности (м ² ).
• $C_{b}$ - числовая концентрация молекул адсорбера (растворенного вещества) в объемном растворе (#/м ³ ).
• D – коэффициент диффузии адсорбера (м ² /с).
• t — прошедшее время (с).
• $\Gamma$ - накопленное количество молекул в единице # молекул, адсорбированных за время $t$.

Уравнение названо в честь американских химиков Ирвинга Ленгмюра и Винсента Шефера .

Кратко, как описано в профиль градиента концентрации вблизи вновь созданного (из $t=0$) поглощающая поверхность (расположена на $x=0$) в некогда однородном объемном растворе решается в приведенных выше разделах из уравнения Фика,

${\frac {\partial C}{\partial x}}={\frac {C_{b}}{\sqrt {\pi Dt}}}{\text{exp}}(-{\frac {x^{2}}{4Dt}})$

• C – численная концентрация молекул адсорбера при $x,t$ (#/м ³ ).

Градиент концентрации в недрах при $x=0$ упрощается до предэкспоненциального коэффициента распределения

$({\frac {\partial C}{\partial x}})_{x=0}={\frac {C_{b}}{\sqrt {\pi Dt}}}$

А скорость диффузии (потока) по площади $A$ самолета

$({\frac {\partial \Gamma }{\partial t}})_{x=0}=-{\frac {DAC_{b}}{\sqrt {\pi Dt}}}$

Интегрируясь с течением времени,

$\Gamma =\int _{0}^{t}({\frac {\partial \Gamma }{\partial t}})_{x=0}=2AC_{b}{\sqrt {\frac {Dt}{\pi }}}$

Уравнение Ленгмюра-Шефера можно расширить до уравнения Уорда-Тордаи, чтобы учесть «обратную диффузию» отброшенных молекул с поверхности:

$\Gamma =2A{C_{\text{b}}}{\sqrt {\frac {Dt}{\pi }}}-A{\sqrt {\frac {D}{\pi }}}\int _{0}^{\sqrt {t}}{\frac {C(\tau )}{\sqrt {t-\tau }}}\,d\tau$

где $C_{b}$ - объемная концентрация, $C$ - подповерхностная концентрация (которая является функцией времени в зависимости от модели реакции адсорбции), и $\tau$ является фиктивной переменной.

Моделирование Монте-Карло показывает, что эти два уравнения работают для прогнозирования скорости адсорбции систем, которые образуют предсказуемые градиенты концентрации вблизи поверхности, но имеют проблемы для систем без или с непредсказуемыми градиентами концентрации, таких как типичные биосенсорные системы или когда поток и конвекция значительны.

Краткая история теорий диффузионной адсорбции.

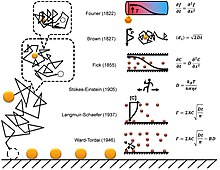
Краткая история диффузной адсорбции показана на рисунке справа. Заметной проблемой понимания диффузионной адсорбции на уровне одиночных молекул является фрактальная природа диффузии. Большинство компьютерных симуляций выбирают временной шаг для диффузии, игнорируя тот факт, что на каждом этапе существуют самоподобные более мелкие события диффузии (фракталы). Моделирование фрактальной диффузии показывает, что в результат моделирования адсорбции с фиксированным шагом по времени следует ввести поправку в два раза, чтобы привести его в соответствие с двумя приведенными выше уравнениями.

Более проблематичный результат приведенных выше уравнений заключается в том, что они предсказывают нижний предел адсорбции в идеальных ситуациях, но очень трудно предсказать фактическую скорость адсорбции. Уравнения получены в долгосрочном условии, когда вблизи поверхности формируется устойчивый градиент концентрации. Но реальная адсорбция часто происходит гораздо быстрее, чем этот бесконечный лимит времени, т. е. градиент концентрации, затухание концентрации в недрах, формируется лишь частично до того, как поверхность насыщается или включается поток для поддержания определенного градиента, таким образом измеренная скорость адсорбции почти всегда выше, чем предсказывают уравнения для адсорбции с низким энергетическим барьером или без него (если только не существует значительного энергетического барьера адсорбции, который значительно замедляет поглощение), например, в тысячи или миллионы раз быстрее при самосборке монослоев на границах раздела вода-воздух или вода-подложка. Таким образом, для практических приложений необходимо рассчитать эволюцию градиента концентрации вблизи поверхности и найти подходящее время, чтобы остановить воображаемую бесконечную эволюцию. Хотя трудно предсказать, когда остановиться, но достаточно легко вычислить самое короткое время, которое имеет значение, критическое время, когда первый ближайший сосед от поверхности подложки почувствует нарастание градиента концентрации. Это дает верхний предел скорости адсорбции в идеальной ситуации, когда нет никаких других факторов, кроме диффузии, влияющих на динамику поглотителя:

$\langle r\rangle ={\frac {4}{\pi }}Ac_{b}^{4/3}D$

• $\langle r\rangle$ — скорость адсорбции в условиях безбарьерной энергии адсорбции, в единицах #/с.
• $A$ - площадь интересующей поверхности на «бесконечной и плоской» подложке (м ² ).
• $C_{b}$ – концентрация молекулы поглотителя в объемном растворе (#/м ³ ).
• $D$ – константа диффузии поглотителя (растворенного вещества) в растворе (м ² /s), определяемый законом Фика.
• Габаритный анализ этих агрегатов выполнен.

Это уравнение можно использовать для прогнозирования начальной скорости адсорбции любой системы; Его можно использовать для прогнозирования стационарной скорости адсорбции типичной биосенсорной системы, когда место связывания составляет лишь очень небольшую часть поверхности подложки и приповерхностный градиент концентрации никогда не формируется; Его также можно использовать для прогнозирования скорости адсорбции молекул на поверхности, когда существует значительный поток, который очень мелко смещает градиент концентрации в недрах.

Это критическое время существенно отличается от времени прибытия первого пассажира или среднего времени свободного пробега. Использование среднего времени первого пассажира и закона диффузии Фика для оценки средней скорости связывания приведет к значительному завышению оценки градиента концентрации, поскольку первый пассажир обычно приходит из многих слоев соседей, удаленных от цели, поэтому время его прибытия значительно больше, чем время диффузии ближайшего соседа. Использование среднего времени свободного пробега плюс уравнение Ленгмюра вызовет искусственный градиент концентрации между начальным местоположением первого пассажира и целевой поверхностью, поскольку другие соседние слои еще не изменились, что значительно занижает оценку фактического времени связывания, т. е. Фактическое время прибытия первого пассажира, обратное указанной выше скорости, рассчитать сложно. Если систему можно упростить до одномерной диффузии, то среднее время первого пассажира можно рассчитать, используя то же критическое время диффузии ближайшего соседа, чтобы расстояние до первого соседа было MSD,

$L={\sqrt {2Dt}}$

• $L~=C_{b}^{-1/3}$ (единица м) — среднее расстояние до ближайшего соседа, аппроксимированное кубической упаковкой, где $C_{b}$ - концентрация растворенного вещества в объемном растворе (ед. # молекула/м ³ ).
• $D$ - коэффициент диффузии, определяемый уравнением Фика (единица м ² /с).
• $t$ – критическое время (ед. с).

В это критическое время маловероятно, что первый пассажир прибыл и адсорбировался. Но он задает скорость прибытия слоев соседей. На этой скорости с градиентом концентрации, который останавливается вокруг первого соседнего слоя, градиент практически не проявляется в течение более длительного времени, когда прибывает фактический первый пассажир. Таким образом, средняя скорость прибытия первого пассажира (количество молекул/с) для этой трехмерной диффузии упрощена в одномерной задаче:

$<r>=a/t=2aC_{b}^{2/3}D$

• $a$ является фактором преобразования трехмерной задачи диффузионной адсорбции в одномерную задачу диффузии, значение которой зависит от системы, например, доли площади адсорбции $A$ над растворенной площадью поверхности сферы ближайшего соседа $4\pi L^{2}/4$ предполагая кубическую упаковку, каждая единица имеет 8 соседей, общих с другими единицами. Этот пример фракции сходится результат к трехмерному решению диффузионной адсорбции, показанному выше, с небольшой разницей в предварительном коэффициенте из-за различных предположений об упаковке и игнорирования других соседей.

Когда область интереса имеет размер молекулы (в частности, длинной цилиндрической молекулы, такой как ДНК), уравнение скорости адсорбции представляет частоту столкновений двух молекул в разбавленном растворе, при этом одна молекула имеет определенную сторону, а другая - нестерическую. зависимость, т. е. молекула (случайная ориентация) ударяется одной стороной о другую. Константу диффузии необходимо обновить до относительной константы диффузии между двумя диффундирующими молекулами. Эта оценка особенно полезна при изучении взаимодействия между небольшой молекулой и более крупной молекулой, такой как белок. В эффективной константе диффузии преобладает меньшая константа диффузии, вместо которой можно использовать константу диффузии.

Приведенное выше уравнение скорости попадания также полезно для прогнозирования кинетики самосборки молекул на поверхности. Молекулы в объеме раствора ориентированы хаотично. Предполагая, что 1/6 молекул имеет правильную ориентацию по отношению к поверхностным местам связывания, т.е. 1/2 направления z в трех измерениях x, y, z, таким образом, интересующая концентрация составляет всего 1/6 от объемной концентрации. Подставив это значение в уравнение, вы сможете рассчитать теоретическую кинетическую кривую адсорбции, используя модель адсорбции Ленгмюра . В более жесткой картине 1/6 можно заменить стерическим фактором геометрии связывания.

Сравнение теории столкновений и теории диффузионных столкновений.

Частота бимолекулярных столкновений, связанная со многими реакциями, включая коагуляцию/агрегацию белков, первоначально описывается уравнением коагуляции Смолуховского , предложенным Марианом Смолуховским в плодотворной публикации 1916 года: выведено из броуновского движения и законов диффузии Фика. В идеализированных условиях реакции для продукта A + B → в разбавленном растворе Смолуховский предположил, что молекулярный поток в бесконечном временном пределе может быть рассчитан на основе законов диффузии Фика, что дает фиксированный / стабильный градиент концентрации от целевой молекулы, например, B равен молекула-мишень удерживается относительно фиксированной, а A - это движущаяся молекула, которая создает градиент концентрации вблизи молекулы-мишени B из-за реакции коагуляции между A и B. Смолуховский рассчитал частоту столкновений между A и B в растворе с единицей #/с. /м ³ :

$Z_{AB}=4{\pi }RD_{r}C_{A}C_{B}$

где,

• $R$ это радиус столкновения
• $D_{r}=D_{A}+D_{B}$ - относительная константа диффузии между A и B (м ² /с)
• $C_{A}$ и $C_{B}$ - числовые концентрации A и B соответственно (#/м ³ ).

Порядок этой бимолекулярной реакции равен 2, что является аналогией результата теории столкновений , когда скорость движения молекулы заменяется диффузионным потоком. В теории столкновений время прохождения между A и B пропорционально расстоянию, что представляет собой аналогичную зависимость для случая диффузии, если поток фиксирован.

Однако на практике градиент концентрации вблизи молекулы-мишени меняется с течением времени, а также развивается молекулярный поток: и в среднем поток намного больше, чем поток бесконечного срока, предложенный Смолуховским. До прибытия первого пассажира уравнение Фика предсказывает градиент концентрации с течением времени, который в действительности еще не накапливается. Таким образом, эта частота Смолуховского представляет собой нижний предел реальной частоты столкновений.

В 2022 году Чен вычисляет верхний предел частоты столкновений между A и B в растворе, предполагая, что объемная концентрация движущейся молекулы фиксирована после первого ближайшего соседа целевой молекулы. Таким образом, эволюция градиента концентрации останавливается на первом ближайшем соседнем слое, учитывая время остановки для расчета фактического потока. Он назвал это время критическим и вывел частоту диффузных столкновений в единицах #/с/м. ³ :

$Z_{AB}={\frac {8}{\pi }}{\sigma }D_{r}C_{A}C_{B}{\sqrt[{3}]{C_{A}+C_{B}}}$

где,

• ${\sigma }$ – площадь поперечного сечения столкновения (м ² ).
• $D_{r}=D_{A}+D_{B}$ - относительная константа диффузии между A и B (м ² /с).
• $C_{A}$ и $C_{B}$ - числовые концентрации A и B соответственно (#/м ³ ).

В этом уравнении предполагается, что верхний предел частоты диффузионных столкновений между A и B наступает тогда, когда первый соседний слой начинает ощущать эволюцию градиента концентрации, порядок реакции которого равен ⁠2 + 1/3 СИ . ⁠ вместо 2. И уравнение Смолуховского, и уравнение Дж.Чена удовлетворяют проверкам размерностей с единицами Но первое зависит от радиуса, а второе — от площади сферы столкновения. В результате анализа размеров получится уравнение, зависящее от объема сферы столкновения, но в конечном итоге все уравнения должны сходиться к одной и той же числовой скорости столкновения, которую можно измерить экспериментально. Фактический порядок реакции для реакции бимолекулярной единицы может составлять от 2 до ⁠2 + 1/3 , что имеет смысл , ⁠ поскольку время диффузионного столкновения прямо зависит от расстояния между двумя молекулами.

Биологическая перспектива

Первый закон приводит к следующей формуле:

${\text{flux}}={-P\left(c_{2}-c_{1}\right)}$

в котором

• P — проницаемость, экспериментально определенная « проводимость » мембраны для данного газа при данной температуре.
• c ₂ − c ₁ – разница концентрации газа через мембрану для направления потока (от c ₁ до c ₂ ).

Первый закон Фика также важен в уравнениях переноса излучения. Однако в этом контексте это становится неточным, когда константа диффузии мала и излучение ограничивается скоростью света, а не сопротивлением материала, через который проходит излучение. В этой ситуации можно использовать ограничитель потока .

Скорость обмена газа через жидкую мембрану можно определить, используя этот закон вместе с законом Грэма .

В условиях разбавленного раствора, когда диффузия берет на себя управление, проницаемость мембраны, упомянутая в предыдущем разделе, может быть теоретически рассчитана для растворенного вещества с использованием уравнения, упомянутого в последнем разделе (используйте с особой осторожностью, поскольку уравнение получено для плотных растворенных веществ, а биологические молекулы не плотнее воды. Кроме того, это уравнение предполагает идеальные формы градиента концентрации вблизи мембраны и развивается с течением времени):

$P=2A_{p}\eta _{tm}{\sqrt {D/(\pi t)}}$

где

• $A_{P}$ – общая площадь пор мембраны (единицы м ² ).
• $\eta _{tm}$ трансмембранная эффективность (безразмерная), которую можно рассчитать на основе стохастической теории хроматографии .
• D - константа диффузии единицы растворенного вещества м ² ⋅s ⁻¹ .
• t – единица времени с.
• концентрацию c ₂ , c ₁ следует использовать в единицах моль м ⁻³ , поэтому единицей потока становится моль с ⁻¹ .

Поток затухает в квадратном корне из времени, поскольку в идеальных условиях вблизи мембраны с течением времени создается градиент концентрации. Когда есть поток и конвекция, поток может значительно отличаться от того, который предсказывает уравнение, и показывать эффективное время t с фиксированным значением, что делает поток стабильным, а не затухающим с течением времени. Критическое время было оценено в идеализированных условиях течения, когда градиент не образуется. Эта стратегия принята в биологии, например, в области кровообращения.

Применение в производстве полупроводников

Полупроводник — это собирательный термин для ряда устройств. В основном он включает в себя три категории: двухполюсные устройства, трехполюсные устройства и четырехполюсные устройства. Комбинация полупроводников называется интегральной схемой.

Связь между законом Фика и полупроводниками: принцип полупроводника заключается в переносе химических веществ или легирующих примесей из слоя в слой. Закон Фика можно использовать для контроля и прогнозирования диффузии, если с помощью математических вычислений узнать, насколько концентрация примесей или химических веществ перемещается за метр в секунду.

Следовательно, можно изготавливать полупроводники разных типов и уровней.

Технологии изготовления интегральных схем , модельные процессы, такие как CVD, термическое окисление, мокрое окисление, легирование и т. д., используют уравнения диффузии, полученные на основе закона Фика.

CVD-метод изготовления полупроводников

Пластина представляет собой разновидность полупроводника, кремниевая подложка которого покрыта слоем полимерной цепи и пленок, созданных методом CVD. Эта пленка содержит легирующие примеси n-типа и p-типа и берет на себя ответственность за легирующую проводимость. Принцип CVD основан на химической реакции газовой фазы и газа с твердым телом для создания тонких пленок.

Режим вязкого течения при CVD обусловлен градиентом давления. CVD также включает диффузионный компонент, отличный от поверхностной диффузии адатомов. При CVD реагенты и продукты также должны диффундировать через пограничный слой застойного газа, который существует рядом с подложкой. Общее количество этапов, необходимых для роста пленки CVD, включает газофазную диффузию реагентов через пограничный слой, адсорбцию и поверхностную диффузию адатомов, реакции на подложке и газофазную диффузию продуктов через пограничный слой.

Профиль скорости потока газа: $$\delta (x)=\left({\frac {5x}{\mathrm {Re} ^{1/2}}}\right)\mathrm {Re} ={\frac {v\rho L}{\eta }}$$где

• $\delta$ это толщина
• $\mathrm {Re}$ это число Рейнольдса
• x — длина подложки
• v = 0 на любой поверхности
• $\eta$ вязкость
• $\rho$ плотность.

Интегрировав x от 0 до L , получим среднюю толщину: $$\delta ={\frac {10L}{3\mathrm {Re} ^{1/2}}}$$

Чтобы реакция была сбалансированной, реагенты должны диффундировать через застойный пограничный слой, чтобы достичь субстрата. Поэтому желателен тонкий пограничный слой. Согласно уравнениям, увеличение vo приведет к увеличению потерь реагентов. Реагенты не будут достигать подложки равномерно, если поток станет турбулентным. Другой вариант — перейти на новый газ-носитель с более низкой вязкостью или плотностью.

Первый закон Фика описывает диффузию через пограничный слой. В зависимости от давления ( P ) и температуры ( T ) в газе определяется диффузия.

$$D=D_{0}\left({\frac {P_{0}}{P}}\right)\left({\frac {T}{T_{0}}}\right)^{3/2}$$где

• $P_{0}$ это стандартное давление
• $T_{0}$ стандартная температура
• $D_{0}$ – стандартный коэффициент диффузии.

Уравнение показывает, что увеличение температуры или уменьшение давления может увеличить коэффициент диффузии.

Первый закон Фика предсказывает поток реагентов к подложке и продукта от подложки: $$J=-D_{i}\left({\frac {dc_{i}}{dx}}\right)$$где

• $x$ это толщина $\delta$
• $dc_{i}$ – концентрация первого реагента.

В законе идеального газа $PV=nRT$, концентрация газа выражается парциальным давлением.

$$J=-D_{i}\left({\frac {P_{i}-P_{0}}{\delta RT}}\right)$$где

• $R$ газовая постоянная
• ${\frac {P_{i}-P_{0}}{\delta }}$ – градиент парциального давления.

В результате первый закон Фика говорит нам, что мы можем использовать градиент парциального давления для контроля диффузии и роста тонких пленок полупроводников.

Во многих реальных ситуациях простой закон Фика не является адекватной формулировкой проблемы полупроводников. Это применимо только к определенным условиям, например, к граничным условиям полупроводника: диффузия с постоянной концентрацией источника, ограниченная концентрация источника или движущаяся граничная диффузия (когда глубина перехода продолжает перемещаться в подложку).

Недействительность фиковской диффузии

Несмотря на то, что диффузия Фика использовалась для моделирования диффузионных процессов в производстве полупроводников (включая CVD-реакторы) в первые дни, она часто не может подтвердить диффузию в современных полупроводниковых узлах (<90 нм). В основном это связано с неспособностью диффузии Фика точно моделировать диффузионные процессы на молекулярном уровне и на меньших уровнях. В передовом производстве полупроводников важно понимать движение на атомном уровне, которое невозможно осуществить при непрерывной диффузии. Сегодня большинство производителей полупроводников используют случайное блуждание для изучения и моделирования процессов диффузии. Это позволяет нам изучать эффекты диффузии дискретным образом, чтобы понять движение отдельных атомов, молекул, плазмы и т. д.

В таком процессе движения диффундирующих веществ (атомов, молекул, плазмы и т. д.) рассматриваются как дискретная сущность, следующая за случайным блужданием через CVD-реактор, пограничный слой, материальные структуры и т. д. Иногда движения могут следовать смещенной закономерности. -случайное блуждание в зависимости от условий обработки. Статистический анализ проводится, чтобы понять вариации/стохастичность, возникающие в результате случайного блуждания видов, что, в свою очередь, влияет на общий процесс и электрические вариации.

Производство продуктов питания и приготовление пищи

Формулировка первого закона Фика может объяснить множество сложных явлений в контексте продуктов питания и приготовления пищи: диффузия таких молекул, как этилен, способствует росту и созреванию растений, молекул соли и сахара способствует засолке и маринованию мяса, а молекулы воды способствуют обезвоживанию. Первый закон Фика также можно использовать для прогнозирования изменения профиля влажности спагетти-лапши по мере ее гидратации во время приготовления. Все эти явления связаны с самопроизвольным движением частиц растворенных веществ под действием градиента концентрации. В разных ситуациях существует разная диффузия, которая является постоянной.

Контролируя градиент концентрации, можно контролировать время приготовления, форму продуктов и посол.

См. также

• Адвекция
• Уравнение Черчилля – Бернштейна
• Диффузия
• Ложная диффузия
• Газообмен
• Массовый поток
• Диффузия Максвелла – Стефана
• Уравнение Нернста – Планка
• Осмос

Дальнейшее чтение

• Берг ХК (1977). Случайные блуждания по биологии . Принстон.
• Берд Р.Б., Стюарт В.Е., Лайтфут Э.Н. (1976). Транспортные явления . Джон Уайли и сыновья.
• Бокштейн Б.С., Менделев М.И., Сроловиц Д.Д., ред. (2005). Термодинамика и кинетика в материаловедении: краткий курс . Оксфорд: Издательство Оксфордского университета. стр. 167–171 .
• Кренк Дж (1980). Математика диффузии . Издательство Оксфордского университета.
• К черту А (1855). «О диффузии жидкости». Анналы физики и химии . 94 : 59. – перепечатано в Фик, Адольф (1995). «О диффузии жидкости». Журнал мембранной науки . 100 : 33–38. дои : 10.1016/0376-7388(94)00230-в .
• Смит В.Ф. (2004). Основы материаловедения и инженерии (3-е изд.). МакГроу-Хилл.

Внешние ссылки

• Уравнения Фика, преобразования Больцмана и т. д. (с рисунками и анимацией)
• Второй закон Фика об OpenStax