Специальная теория относительности

| Специальная теория относительности |
|---|
 |
В физике специальная теория относительности , или сокращенно специальная теория относительности , представляет собой научную теорию связи между пространством и временем . В трактовке Альберта Эйнштейна 1905 года теория представлена как основанная всего на двух постулатах : [стр 1] [1] [2]
- Законы физики инвариантны ( идентичны ) во всех инерциальных системах отсчета (то есть системах отсчета без ускорения ).
- Скорость света в вакууме одинакова для всех наблюдателей, независимо от движения источника света или наблюдателя.
Первый постулат впервые был сформулирован Галилео Галилеем (см. Инвариантность Галилея ).
Происхождение и значение
[ редактировать ]Специальная теория относительности была описана Альбертом Эйнштейном в статье « К электродинамике движущихся тел », опубликованной 26 сентября 1905 года. [стр 1] оказались Максвелла Уравнения электромагнетизма несовместимыми с ньютоновской механикой , а эксперимент Майкельсона-Морли не смог обнаружить движение Земли против гипотетического светоносного эфира . Это привело к разработке преобразований Лоренца , которые корректируют расстояния и время для движущихся объектов. Специальная теория относительности корректирует существовавшие до сих пор законы механики, чтобы обрабатывать ситуации, включающие все движения, особенно те, которые происходят со скоростью, близкой к скорости света (известные как релятивистские скорости ). Сегодня доказано, что специальная теория относительности является наиболее точной моделью движения на любой скорости, когда гравитационные и квантовые эффекты незначительны. [3] [4] Несмотря на это, ньютоновская модель по-прежнему актуальна как простое и точное приближение при низких скоростях (относительно скорости света), например, при повседневных движениях на Земле.
Специальная теория относительности имеет широкий спектр следствий, подтвержденных экспериментально. [5] К ним относятся относительность одновременности , сокращение длины , замедление времени , релятивистская формула сложения скоростей, релятивистский эффект Доплера , релятивистская масса , универсальный предел скорости , эквивалентность массы и энергии , скорость причинности и прецессия Томаса . [1] [2] Например, оно заменило традиционное понятие абсолютного всемирного времени понятием времени, которое зависит от системы отсчета и пространственного положения. Вместо инвариантного временного интервала между двумя событиями существует инвариантный пространственно-временной интервал . В сочетании с другими законами физики два постулата специальной теории относительности предсказывают эквивалентность массы и энергии , как это выражено в эквивалентности массы и энергии. формуле , где это скорость света в вакууме. [6] [7] Это также объясняет, как связаны явления электричества и магнетизма. [1] [2]
Определяющей особенностью специальной теории относительности является замена преобразований Галилея механики Ньютона преобразованиями Лоренца . Время и пространство не могут быть определены отдельно друг от друга (как считалось ранее). Скорее, пространство и время переплетаются в единый континуум, известный как «пространство-время» . События, происходящие одновременно для одного наблюдателя, могут происходить в разное время для другого.
До тех пор, пока несколько лет спустя Эйнштейн не разработал общую теорию относительности , которая ввела искривленное пространство-время для включения гравитации, фраза «специальная теория относительности» не использовалась. Иногда используется перевод «ограниченная теория относительности»; «Особый» на самом деле означает «особый случай». [стр. 2] [стр. 3] [стр. 4] [примечание 1] Некоторые работы Альберта Эйнштейна по специальной теории относительности основаны на более ранних работах Хендрика Лоренца и Анри Пуанкаре . Теория стала практически завершенной в 1907 году, когда появились Германа Минковского о пространстве-времени. статьи [4]
Теория является «особой» в том смысле, что она применима только в частном случае , когда пространство-время «плоское», то есть когда кривизна пространства-времени (следствие тензора энергии-импульса и представление гравитации ) незначительна. [8] [примечание 2] Чтобы правильно учесть гравитацию, Эйнштейн в 1915 году сформулировал общую теорию относительности. Специальная теория относительности, вопреки некоторым историческим описаниям, действительно учитывает как ускорения, так и ускоряющиеся системы отсчета . [9] [10]
Точно так же, как теория относительности Галилея сейчас считается приближением специальной теории относительности, справедливой для малых скоростей, специальная теория относительности считается приближением общей теории относительности, справедливой для слабых гравитационных полей , то есть в достаточно малом масштабе (например, когда приливные силы незначительны) и в условиях свободного падения . Но общая теория относительности включает неевклидову геометрию , чтобы представить гравитационные эффекты как геометрическую кривизну пространства-времени. Специальная теория относительности ограничена плоским пространством-временем, известным как пространство Минковского . Пока Вселенную можно смоделировать как псевдориманово многообразие , лоренц-инвариантную систему отсчета, которая подчиняется специальной теории относительности, можно определить для достаточно малой окрестности каждой точки в этом искривленном пространстве-времени .
Галилео Галилей уже постулировал, что не существует абсолютного и четко определенного состояния покоя (нет привилегированных систем отсчета ), принцип, который теперь называется принципом относительности Галилея . Эйнштейн расширил этот принцип так, что он объяснил постоянную скорость света. [11] явление, которое наблюдалось в эксперименте Майкельсона-Морли. Он также постулировал, что это справедливо для всех законов физики , включая законы механики и электродинамики . [12]
Традиционный подход к специальной теории относительности «двух постулатов».
[ редактировать ]«Размышления такого рода дали мне понять уже вскоре после 1900 года, т. е. вскоре после новаторской работы Планка, что ни механика, ни электродинамика не могут (за исключением предельных случаев) претендовать на точную достоверность. Постепенно я отчаялся в возможности открытия истинные законы посредством конструктивных усилий, основанных на известных фактах. Чем дольше и отчаяннее я пытался, тем больше я приходил к убеждению, что только открытие универсального формального принципа может привести нас к гарантированным результатам... Как же тогда? , можно ли найти такой универсальный принцип?»
Альберт Эйнштейн: Автобиографические заметки [стр. 5]
Эйнштейн выделил два фундаментальных положения, которые казались наиболее достоверными, независимо от точной справедливости известных (тогда) законов механики или электродинамики. Этими положениями были постоянство скорости света в вакууме и независимость физических законов (особенно постоянства скорости света) от выбора инерциальной системы. В своей первой презентации специальной теории относительности в 1905 году он выразил эти постулаты следующим образом: [стр 1]
- Принцип относительности – на законы, по которым изменяются состояния физических систем, не влияет, относятся ли эти изменения состояния к той или иной из двух систем, находящихся в равномерном поступательном движении относительно друг друга. [стр 1]
- Принцип инвариантности скорости света – «...свет всегда распространяется в пустом пространстве с определенной скоростью [скоростью] c , которая не зависит от состояния движения излучающего тела» (из предисловия). [стр 1] То есть свет в вакууме распространяется со скоростью c (фиксированной постоянной, не зависящей от направления) по крайней мере в одной системе инерциальных координат («стационарной системе»), независимо от состояния движения источника света.
Постоянство скорости света было мотивировано теорией электромагнетизма Максвелла. [13] и отсутствие доказательств существования светоносного эфира . [14] Существуют противоречивые данные о том, в какой степени на Эйнштейна повлиял нулевой результат эксперимента Майкельсона-Морли. [15] [16] В любом случае нулевой результат эксперимента Майкельсона-Морли помог идее постоянства скорости света получить широкое и быстрое признание.
Вывод специальной теории относительности зависит не только от этих двух явных постулатов, но и от нескольких неявных предположений ( сделанных почти во всех теориях физики ), включая изотропность и однородность пространства и независимость измерительных стержней и часов от их прошлой истории. [стр. 6]
После первоначального представления специальной теории относительности Эйнштейном в 1905 году было предложено множество различных наборов постулатов в различных альтернативных вариантах. [17] Но наиболее распространенным набором постулатов остаются те, которые использовал Эйнштейн в своей оригинальной статье. Более математическое изложение принципа относительности, сделанное позднее Эйнштейном и вводящее не упомянутую выше концепцию простоты, звучит так:
Специальный принцип относительности : если система координат K выбрана так, что по отношению к ней действуют физические законы в своей простейшей форме, то те же законы справедливы и по отношению к любой другой системе координат K ', движущейся равномерно поступательно относительно к К. [18]
Анри Пуанкаре обеспечил математическую основу теории относительности, доказав, что преобразования Лоренца являются подмножеством его Пуанкаре группы преобразований симметрии . Позже Эйнштейн вывел эти преобразования из своих аксиом.
Во многих статьях Эйнштейна представлены выводы преобразования Лоренца, основанные на этих двух принципах. [стр. 7]
Принцип относительности
[ редактировать ]Системы отсчета и относительное движение
[ редактировать ]
Системы отсчета играют решающую роль в теории относительности. Используемый здесь термин «система отсчета» представляет собой перспективу наблюдения в пространстве, не претерпевающую никаких изменений в движении (ускорении), из которой можно измерить положение вдоль трех пространственных осей (то есть в состоянии покоя или с постоянной скоростью). Кроме того, система отсчета имеет возможность определять измерения времени событий с помощью «часов» (любого отсчетного устройства с равномерной периодичностью).
Событие — это событие , которому можно присвоить единственный уникальный момент и местоположение в пространстве относительно системы отсчета: это «точка» в пространстве-времени . Поскольку скорость света постоянна в теории относительности независимо от системы отсчета, импульсы света можно использовать для однозначного измерения расстояний и отсчета времени, когда события произошли с часами, даже если свету требуется время, чтобы достичь часов после события. произошло.
Например, взрыв петарды можно считать «событием». Мы можем полностью определить событие по его четырем пространственно-временным координатам: время возникновения и его трехмерное пространственное положение определяют точку отсчета. Назовем эту систему S. отсчета
В теории относительности мы часто хотим вычислить координаты события из разных систем отсчета. Уравнения, связывающие измерения, выполненные в разных системах отсчета, называются уравнениями преобразования .
Стандартная конфигурация
[ редактировать ]Чтобы получить представление о том, как координаты пространства-времени, измеренные наблюдателями в разных системах отсчета, соотносятся друг с другом, полезно работать с упрощенной установкой с системами стандартной конфигурации . [19] : 107 При осторожном подходе это позволяет упростить математические расчеты без потери общности полученных выводов. На рис. 2-1 две системы отсчета Галилея (т.е. обычные трехмерные системы координат) показаны в относительном движении. Кадр S принадлежит первому наблюдателю O , а кадр S ′ (произносится как «S Prime» или «S Dash») принадлежит второму наблюдателю O ′ .
- Оси x , y , z кадра S ориентированы параллельно соответствующим осям со штрихом кадра S ' .
- Для простоты кадр S ' движется в одном направлении: в направлении x кадра S с постоянной скоростью v измеренной в кадре S. ,
- Начало кадров S и S ′ совпадает, когда время t = 0 для кадра S и t ′ = 0 для кадра S ′ .
Поскольку в теории относительности не существует абсолютной системы отсчета, понятия «движение» строго не существует, поскольку все может двигаться относительно какой-то другой системы отсчета. Вместо этого говорят, что любые два кадра, которые движутся с одинаковой скоростью в одном направлении, движутся навстречу друг другу . Следовательно, S и S ’ не движутся вместе .
Отсутствие абсолютной системы отсчета.
[ редактировать ]Принцип относительности , который утверждает, что физические законы имеют одинаковую форму в каждой инерциальной системе отсчета , восходит к Галилею и был включен в ньютоновскую физику. Но в конце 19 века существование электромагнитных волн побудило некоторых физиков предположить, что Вселенная наполнена веществом, которое они назвали « эфиром », которое, как они постулировали, должно действовать как среда, через которую распространяются эти волны или вибрации ( во многом аналогично тому, как звук распространяется в воздухе). Считалось, что эфир является абсолютной системой отсчета , относительно которой можно измерить все скорости, и его можно было считать фиксированным и неподвижным относительно Земли или какой-либо другой фиксированной точки отсчета. Эфир должен был быть достаточно эластичным, чтобы поддерживать электромагнитные волны, в то время как эти волны могли взаимодействовать с материей, не оказывая при этом сопротивления проходящим через него телам (его единственным свойством было то, что он позволял распространяться электромагнитным волнам). Результаты различных экспериментов, в том числе эксперимента Майкельсона-Морли в 1887 году (впоследствии подтвержденного более точными и новаторскими экспериментами), привели к созданию специальной теории относительности, показав, что эфира не существует. [20] Решением Эйнштейна было отказаться от понятия эфира и абсолютного состояния покоя. В теории относительности любая система отсчета, движущаяся равномерно, подчиняется одним и тем же законам физики. В частности, скорость света в вакууме всегда измеряется как c , даже если ее измеряют несколько систем, движущихся с разными (но постоянными) скоростями.
Относительность без второго постулата
[ редактировать ]Только на основе принципа относительности, не предполагая постоянства скорости света (т. е. используя изотропию пространства и симметрию, подразумеваемую принципом специальной теории относительности), можно показать , что преобразования пространства-времени между инерциальными системами отсчета являются либо евклидовыми, либо галилеевскими. , или лоренциан. В лоренцевом случае тогда можно получить сохранение релятивистского интервала и некоторую конечную предельную скорость. Эксперименты показывают, что эта скорость равна скорости света в вакууме. [стр. 8] [21]
Лоренц-инвариантность как основное ядро специальной теории относительности
[ редактировать ]Альтернативные подходы к специальной теории относительности
[ редактировать ]Эйнштейн последовательно основывал вывод лоренц-инвариантности (основного ядра специальной теории относительности) только на двух основных принципах теории относительности и инвариантности скорости света. Он написал:
Фундаментальное для специальной теории относительности положение таково: предположения относительности и инвариантности скорости света совместимы, если постулируются соотношения нового типа («преобразование Лоренца») для преобразования координат и времен событий... Универсальный принцип Специальной теории относительности содержится в постулате: Законы физики инвариантны относительно преобразований Лоренца (при переходе от одной инерциальной системы к любой другой, произвольно выбранной инерциальной системе). Это ограничивающий принцип для естественных законов... [стр. 5]
Таким образом, многие современные трактовки специальной теории относительности основывают ее на единственном постулате универсальной ковариантности Лоренца или, что то же самое, на единственном постулате пространства-времени Минковского . [стр. 9] [стр. 10]
Вместо того, чтобы рассматривать универсальную ковариацию Лоренца как производный принцип, в этой статье она рассматривается как фундаментальный постулат специальной теории относительности. Традиционный подход к специальной теории относительности, основанный на двух постулатах, представлен в бесчисленных учебниках для колледжей и популярных презентациях. [22] Учебники, начинающиеся с единственного постулата пространства-времени Минковского, включают учебники Тейлора и Уиллера. [23] и Каллахан. [24] Этому же подходу следуют статьи Википедии «Пространство-время» и «Диаграмма Минковского» .
Преобразование Лоренца и его обратное.
[ редактировать ]Определите событие , чтобы оно имело пространственно-временные координаты ( t , x , y , z ) в системе S и ( t ' , x ' , y ' , z ' ) в системе отсчета, движущейся со скоростью v по оси x относительно этот кадр, S ′ . Тогда преобразование Лоренца указывает, что эти координаты связаны следующим образом: где – фактор Лоренца , c – скорость света а скорость v S ′ в вакууме , относительно S параллельна оси x . Для простоты координаты y и z не затрагиваются; только координаты x и t преобразуются . Эти преобразования Лоренца образуют однопараметрическую группу , линейных отображений этот параметр называется быстротой .
Решение четырех приведенных выше уравнений преобразования для координат без штриха дает обратное преобразование Лоренца:
Это показывает, что кадр без штриха движется со скоростью - v , измеренной в кадре со штрихом. [25]
нет ничего особенного В оси X . Преобразование может применяться к осям y или z , или даже в любом направлении, параллельном движению (которое искривляется фактором γ ) и перпендикулярно; см. в статье «Преобразование Лоренца» Подробности .
Величина, инвариантная относительно преобразований Лоренца , известна как скаляр Лоренца .
Записывая преобразование Лоренца и обратное ему через разность координат, где одно событие имеет координаты ( x 1 , t 1 ) и ( x ′ 1 , t ′ 1 ) , другое событие имеет координаты ( x 2 , t 2 ) и ( x ′ 2 , t ′ 2 ) , а разности определяются как
- уравнение 1:
- уравнение 2:
мы получаем
- уравнение 3:
- уравнение 4:
Если вместо разностей мы возьмем дифференциалы, мы получим
- уравнение 5:
- уравнение 6:
Графическое представление преобразования Лоренца
[ редактировать ]Диаграммы пространства-времени ( диаграммы Минковского ) являются чрезвычайно полезным средством визуализации того, как преобразуются координаты между различными системами отсчета. Хотя выполнить точные вычисления с их помощью не так просто, как с прямым вызовом преобразований Лоренца, их главная сила — это способность обеспечить интуитивное понимание результатов релятивистского сценария. [21]
Чтобы нарисовать диаграмму пространства-времени, начните с рассмотрения двух систем отсчета Галилея, S и S', в стандартной конфигурации, как показано на рис. 2-1. [21] [26] : 155–199
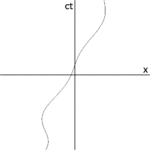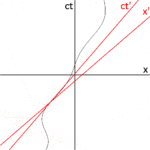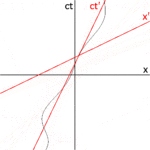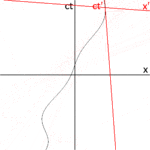
Рис. 3-1а . Нарисуйте и оси рамки S. ось горизонтальна, а (на самом деле ) ось вертикальна, что противоречит обычному соглашению в кинематике. ось масштабируется с коэффициентом так что обе оси имеют общие единицы длины. На показанной диаграмме линии сетки расположены на расстоянии одной единицы друг от друга. Диагональные линии под углом 45° представляют собой мировые линии двух фотонов, проходящих через начало координат в определенный момент времени. Наклон этих мировых линий равен 1, поскольку фотоны перемещаются в пространстве на одну единицу за единицу времени. Два события, и были нанесены на этот график, чтобы их координаты можно было сравнить в кадрах S и S'.
Рис. 3-1б . Нарисуйте и оси системы S'. Ось представляет мировую линию начала системы координат S, измеренную в системе отсчета S. На этом рисунке Оба и оси наклонены от незаштрихованных осей на угол где Оси со штрихом и без штриха имеют общее начало, поскольку кадры S и S' были настроены в стандартной конфигурации, так что когда
Рис. 3-1в . Единицы измерения на заштрихованных осях имеют другой масштаб, чем единицы измерения на незаштрихованных осях. Из преобразований Лоренца мы видим, что координаты в штрихованной системе координат преобразуются в в незаштрихованной системе координат. Так же, координаты в штрихованной системе координат преобразуются в в неосновной системе. Рисовать линии сетки параллельно ось через точки как измерено в незаштрихованной рамке, где является целым числом. Аналогичным образом нарисуйте линии сетки параллельно ось через как измерено в незаштрихованной рамке. Используя теорему Пифагора, мы наблюдаем, что расстояние между единицы равны раз больше расстояния между единиц, измеренных в системе отсчета S. Это соотношение всегда больше 1 и в конечном итоге приближается к бесконечности как
Рис. 3-1г . Поскольку скорость света является инвариантом, мировые линии двух фотонов, проходящих через начало координат в момент времени по-прежнему изображайте диагональные линии под углом 45 °. Заштрихованные координаты и связаны с координатами без штриха посредством преобразований Лоренца и могут быть приблизительно измерены по графику (при условии, что он построен достаточно точно), но настоящее достоинство диаграммы Минковского заключается в том, что она дает нам геометрическое представление о сценарии. Например, на этом рисунке мы видим, что два разделенных во времени события, которые имели разные координаты x в незаштрихованном кадре, теперь находятся в одном и том же положении в пространстве.
В то время как незаштрихованный кадр рисуется с осями пространства и времени, пересекающимися под прямыми углами, заштрихованный кадр рисуется с осями, которые пересекаются под острыми или тупыми углами. Эта асимметрия возникает из-за неизбежных искажений в том, как координаты пространства-времени отображаются на декартовой плоскости , но на самом деле системы отсчета эквивалентны.
Следствия, вытекающие из преобразования Лоренца
[ редактировать ]Следствия специальной теории относительности можно вывести из уравнений преобразования Лоренца . [27] Эти преобразования, а, следовательно, и специальная теория относительности, приводят к физическим предсказаниям, отличным от предсказаний ньютоновской механики при всех относительных скоростях, и наиболее ярко выражены, когда относительные скорости становятся сравнимыми со скоростью света. Скорость света настолько превышает все, с чем сталкивается большинство людей, что некоторые из эффектов, предсказанных теорией относительности, поначалу противоречат здравому смыслу .
Инвариантный интервал
[ редактировать ]В теории относительности Галилея длина объекта ( ) [примечание 3] и временное разделение между двумя событиями ( ) являются независимыми инвариантами, значения которых не изменяются при наблюдении из разных систем отсчета. [примечание 4] [примечание 5]
Однако в специальной теории относительности переплетение пространственных и временных координат порождает концепцию инвариантного интервала , обозначаемого как : [примечание 6]
Переплетение пространства и времени отменяет неявно принятые концепции абсолютной одновременности и синхронизации между несмежными кадрами.
Форма будучи разницей квадрата промежутка времени и квадрата пространственного расстояния, демонстрирует фундаментальное несоответствие между евклидовым и пространственно-временным расстояниями. [примечание 7] Инвариантность этого интервала является свойством общего преобразования Лоренца (также называемого преобразованием Пуанкаре ), что делает его изометрией пространства-времени. Общее преобразование Лоренца расширяет стандартное преобразование Лоренца (которое имеет дело с перемещениями без вращения, то есть усилением Лоренца в направлении x) всеми другими перемещениями , отражениями и вращениями между любой декартовой инерциальной системой отсчета. [31] : 33–34
При анализе упрощенных сценариев, таких как пространственно-временные диаграммы, часто используется форма инвариантного интервала с уменьшенной размерностью:
Продемонстрировать, что интервал инвариантен, несложно для случая пониженной размерности и с кадрами в стандартной конфигурации: [21]
Стоимость следовательно, не зависит от системы отсчета, в которой он измеряется.
Учитывая физическое значение , следует отметить три случая: [21] [32] : 25–39
- Δс 2 > 0: В этом случае два события разделены большим временем, чем пространством, и, следовательно, о них говорят, что они разделены во времениподобно . Это означает, что и учитывая преобразование Лоренца очевидно, что существует меньше, чем для чего (в частности, ). Другими словами, учитывая два события, разделенные во времени, можно найти кадр, в котором эти два события происходят в одном и том же месте. В этом кадре разделение во времени, называется собственным временем .
- Δс 2 < 0: В этом случае два события разделены большим пространством, чем временем, и поэтому говорят, что они разделены пространственноподобно . Это означает, что и учитывая преобразование Лоренца существует меньше, чем для чего (в частности, ). Другими словами, учитывая два события, разделенных пространством, можно найти кадр, в котором эти два события происходят одновременно. В этом кадре разлука в пространстве, называется правильным расстоянием или правильной длиной . Для значений больше и меньше чем знак меняется, то есть временной порядок пространственно-подобных событий меняется в зависимости от кадра, в котором события рассматриваются. Но временной порядок событий, разделенных во времениподобным образом, абсолютен, поскольку единственный способ может быть больше, чем было бы, если бы
- Δс 2 = 0: В этом случае говорят, что два события разделены светоподобно . Это означает, что и это соотношение не зависит от системы координат из-за инвариантности Отсюда мы видим, что скорость света равна в каждой инерциальной системе отсчета. Другими словами, исходя из предположения об универсальной ковариации Лоренца, постоянная скорость света является производным результатом, а не постулатом, как в формулировке специальной теории с двумя постулатами.
Относительность одновременности
[ редактировать ]
Рассмотрим два события, происходящие в двух разных местах одновременно в системе отсчета одного инерциального наблюдателя. Они могут возникнуть неодновременно в системе отсчета другого инерциального наблюдателя (отсутствие абсолютной одновременности ).
Из уравнения 3 (прямое преобразование Лоренца с точки зрения разности координат)
Ясно, что два события, которые одновременны в системе отсчета = 0 ) S (удовлетворяющие Δt , не обязательно одновременны в другой инерциальной системе отсчета ' ( удовлетворяющей Δt ' S = 0 ). Только если эти события дополнительно локальны в кадре S (удовлетворяющие Δx кадре = 0 ), они будут одновременными в другом S ' .
Эффект Саньяка можно считать проявлением относительности одновременности. [33] Поскольку относительность одновременности является эффектом первого порядка в , [21] инструменты, основанные на эффекте Саньяка для своей работы, такие как кольцевые лазерные гироскопы и волоконно-оптические гироскопы , способны достигать экстремальных уровней чувствительности. [стр. 14]
Замедление времени
[ редактировать ]Промежуток времени между двумя событиями не инвариантен от одного наблюдателя к другому, но зависит от относительных скоростей систем отсчета наблюдателей.
Предположим, что покоятся в незаштрихованной системе S. часы Тогда положение часов на двух разных тактах характеризуется Δ x = 0 . Чтобы найти связь между временем между этими тактами, измеренным в обеих системах, уравнение 3, можно использовать чтобы найти:
- для мероприятий, удовлетворяющих
Это показывает, что время (Δt ' ) между двумя тактами, как видно в кадре, в котором движутся часы ( S ' ), больше , чем время (Δt ) между этими тактами, измеренное в остальном кадре часы ( С ). Замедление времени объясняет ряд физических явлений; например, время жизни высокоскоростных мюонов , созданных при столкновении космических лучей с частицами во внешней атмосфере Земли и движущихся к поверхности, больше, чем время жизни медленно движущихся мюонов, созданных и распадающихся в лаборатории. [34]

Всякий раз, когда кто-то слышит утверждение о том, что «движущиеся часы идут медленно», ему следует представить себе инерциальную систему отсчета, густо населенную идентичными синхронизированными часами. Когда движущиеся часы проходят через этот массив, их показания в любой конкретной точке сравниваются с показаниями неподвижных часов в той же точке. [35] : 149–152
Измерения, которые мы получили бы, если бы на самом деле посмотрели на движущиеся часы, в общем, были бы совсем не теми же самыми, потому что время, которое мы видели бы, задерживалось бы из-за конечной скорости света, т.е. искажаться эффектом Доплера . Измерения релятивистских эффектов всегда следует понимать как выполненные после исключения эффектов конечной скорости света. [35] : 149–152
Световые часы Ланжевена
[ редактировать ]
Поль Ланжевен , один из первых сторонников теории относительности, много сделал для популяризации теории, несмотря на сопротивление многих физиков революционным концепциям Эйнштейна. Среди его многочисленных вкладов в основы специальной теории относительности были независимая работа по взаимосвязи массы и энергии, тщательное исследование парадокса близнецов и исследования вращающихся систем координат. Его имя часто связывают с гипотетической конструкцией, называемой «световые часы» (первоначально разработанной Льюисом и Толманом в 1909 году). [36] ), который он использовал для нового вывода преобразования Лоренца. [37]
Световые часы представляют собой коробку с идеально отражающими стенами, в которой световой сигнал отражается взад и вперед от противоположных сторон. Концепция замедления времени часто преподается с использованием световых часов, которые движутся по равномерной инерции, перпендикулярно линии, соединяющей два зеркала. [38] [39] [40] [41] (Сам Ланжевен пользовался световыми часами, ориентированными параллельно линии их движения. [37] )
Рассмотрим сценарий, показанный на рис. 4-3А. Наблюдатель А держит световые часы длиной а также электронный таймер, с помощью которого она измеряет, сколько времени требуется пульсу, чтобы пройти туда и обратно по световым часам. Хотя наблюдатель А быстро движется по поезду, с его точки зрения, испускание и получение импульса происходят в одном и том же месте, и он измеряет интервал с помощью одних часов, расположенных точно в месте этих двух событий. Для интервала между этими двумя событиями наблюдатель А находит Интервал времени, измеряемый с помощью одних часов, неподвижных в определенной системе отсчета, называется собственным интервалом времени . [42]
Рис. 4-3B иллюстрирует эти же два события с точки зрения наблюдателя B, который припарковался у путей, когда поезд проезжает со скоростью Вместо того чтобы совершать прямые движения вверх и вниз, наблюдатель Б видит, как импульсы движутся по зигзагообразной линии. Однако из-за постулата постоянства скорости света скорость импульсов вдоль этих диагональных линий одинакова это наблюдатель А видел по ее пульсу вверх и вниз. B измеряет скорость вертикальной составляющей этих импульсов как так что общее время прохождения импульсов туда и обратно равно Обратите внимание, что для наблюдателя Б испускание и получение светового импульса происходило в разных местах, и он измерял интервал с помощью двух стационарных и синхронизированных часов, расположенных в двух разных положениях его системы отсчета. Таким образом, интервал, который измерял B, не был подходящим временным интервалом, поскольку он не измерял его с помощью одних покоящихся часов. [42]
Взаимное замедление времени
[ редактировать ]В приведенном выше описании световых часов Ланжевена обозначение одного наблюдателя как неподвижного, а другого как движущегося было совершенно произвольным. С таким же успехом можно было бы представить наблюдателя Б, несущего световые часы и движущегося со скоростью влево, и в этом случае наблюдатель A будет воспринимать часы B как идущие медленнее, чем ее местные часы.
Здесь нет парадокса, потому что не существует независимого наблюдателя C, который был бы согласен и с A, и с B. Наблюдатель C обязательно производит свои измерения из своей собственной системы отсчета. Если эта система отсчета совпадает с системой отсчета A, то C будет соответствовать измерению времени A. Если система отсчета C совпадает с системой отсчета B, то C согласуется с измерением времени B. Если система отсчета C не совпадает ни с системой отсчета A, ни с системой B, то измерение времени C не будет расходиться с измерением времени как A, так и B. [43]
Парадокс близнецов
[ редактировать ]Взаимное замедление времени между двумя наблюдателями в отдельных инерциальных системах отсчета приводит к так называемому парадоксу близнецов , сформулированному в его нынешней форме Ланжевеном в 1911 году. [44] Ланжевен представлял себе авантюриста, желающего исследовать будущее Земли. Этот путешественник садится на снаряд, способный двигаться со скоростью 99,995% скорости света. Совершив путешествие туда и обратно к ближайшей звезде и обратно, продолжавшееся всего два года его собственной жизни, он возвращается на Землю, которая на двести лет старше.
Этот результат кажется загадочным, поскольку и путешественник, и наблюдатель с Земли видели бы другого движущимся, и поэтому из-за взаимного замедления времени можно было бы первоначально ожидать, что каждый из них должен был обнаружить, что другой постарел меньше. В действительности никакого парадокса вообще нет, поскольку для того, чтобы два наблюдателя могли сравнить свои собственные времена, необходимо нарушить симметрию ситуации: по крайней мере один из двух наблюдателей должен изменить свое состояние движения так, чтобы оно соответствовало состоянию движения второго наблюдателя. другой. [45]

Однако знание общего разрешения парадокса не дает сразу возможности вычислить правильные количественные результаты. Многие решения этой загадки были предложены в литературе и рассмотрены в статье «Парадокс близнецов» . Ниже мы рассмотрим одно из таких решений парадокса.
Нашей основной целью будет продемонстрировать, что после поездки оба близнеца пришли к полному согласию относительно того, кто и насколько постарел, независимо от их разного опыта. Рис. 4-4 иллюстрирует сценарий, в котором путешествующий двойник летит на расстоянии 0,6 c к звезде и от нее, находящейся на расстоянии 3 лет . Во время путешествия каждый близнец посылает друг другу ежегодные сигналы времени (измеренные в их собственном времени). После поездки совокупные значения сравниваются. На исходной фазе путешествия каждый близнец получает сигналы другого с пониженной скоростью. Первоначально ситуация совершенно симметрична: обратите внимание, что каждый близнец получает годовой сигнал другого через два года, измеренные по их собственным часам. Симметрия нарушается, когда путешествующий близнец разворачивается на отметке четырех лет, измеренной ее часами. В течение оставшихся четырех лет своего путешествия она получает сигналы с повышенной скоростью. Совершенно иначе обстоит дело со стационарным двойником. Из-за задержки со скоростью света он не видит, как его сестра обернулась, пока по его собственным часам не пройдет восемь лет. Таким образом, он получает усиленные сигналы от своей сестры лишь в течение относительно короткого периода времени. Хотя близнецы расходятся в своих измерениях общего времени, мы видим из следующей таблицы, а также путем простого наблюдения диаграммы Минковского, что каждый близнец полностью согласуется с другим относительно общего количества сигналов, отправленных от одного близнеца. другому. Следовательно, никакого парадокса нет. [35] : 152–159
| Элемент | Измерено сидеть дома | Рис. 4-4 | Измерено путешественник | Рис. 4-4 |
|---|---|---|---|---|
| Общее время поездки | 10 лет | 8 лет | ||
| Общее количество отправленных импульсов | 10 | 8 | ||
| поворот путешественника Время, когда обнаружен | 8 лет | 4 | ||
| Количество импульсов, полученных в начале ставка | | 4 | | 2 |
| Время до конца поездки | 2 года | 4 | ||
| Количество сигналов, полученных в финале ставка | 4 | 8 | ||
| Общее количество полученных импульсов | 8 | 10 | ||
| Расчет близнеца относительно того, насколько другой должен был постареть близнец | 8 лет | 10 лет |
Сокращение длины
[ редактировать ]Размеры (например, длина) объекта, измеренные одним наблюдателем, могут быть меньше, чем результаты измерений того же объекта, сделанные другим наблюдателем (например, парадокс лестницы предполагает, что длинная лестница движется со скоростью, близкой к скорости света, и удерживается в небольшом гараже).
Аналогично предположим, что измерительный стержень покоится и выровнен вдоль оси x в незаштрихованной S. системе В этой системе длина этого стержня записывается как Δx . Для измерения длины этого стержня в системе S ' , в которой стержень движется, необходимо одновременно измерить расстояния x ' до концов стержня в этой системе S ' . Другими словами, измерение характеризуется Δ t ′ = 0 , что можно объединить с уравнением 4, чтобы найти связь между длинами Δ x и Δ x ′ :
- для мероприятий, удовлетворяющих
Это показывает, что длина (Δ x ′ ) стержня, измеренная в системе отсчета, в которой он движется ( S ′ ), короче , чем его длина (Δ x ) в собственной системе отсчета покоя ( S ).
Замедление времени и сокращение длины — это не просто видимость. Замедление времени явно связано с нашим способом измерения временных интервалов между событиями, которые происходят в одном и том же месте в данной системе координат (так называемые «совместные» события). Эти временные интервалы (которые могут быть и фактически измерены экспериментально соответствующими наблюдателями) различны в другой системе координат, движущейся относительно первой, если только события, помимо того, что они колокальны, еще и одновременны. Точно так же сокращение длины связано с измеренными нами расстояниями между отдельными, но одновременными событиями в выбранной системе координат. Если эти события не локальны, а разделены расстоянием (пространством), они не будут происходить на одинаковом пространственном расстоянии друг от друга, если смотреть из другой движущейся системы координат.
Лоренц преобразование скоростей
[ редактировать ]Рассмотрим два кадра S и S ′ в стандартной конфигурации. Частица в S движется в направлении x с вектором скорости Какова его скорость в кадре S ' ?
Мы можем написать
| ( 7 ) |
| (8) |
Substituting expressions for and from Equation 5 into Equation 8, followed by straightforward mathematical manipulations and back-substitution from Equation 7 yields the Lorentz transformation of the speed to :
| (9) |
The inverse relation is obtained by interchanging the primed and unprimed symbols and replacing with
| (10) |
For not aligned along the x-axis, we write:[12]: 47–49
| (11) |
| (12) |
The forward and inverse transformations for this case are:
| (13) |
| (14) |
Equation 10 and Equation 14 can be interpreted as giving the resultant of the two velocities and and they replace the formula which is valid in Galilean relativity. Interpreted in such a fashion, they are commonly referred to as the relativistic velocity addition (or composition) formulas, valid for the three axes of S and S′ being aligned with each other (although not necessarily in standard configuration).[12]: 47–49
We note the following points:
- If an object (e.g., a photon) were moving at the speed of light in one frame (i.e., u = ±c or u′ = ±c), then it would also be moving at the speed of light in any other frame, moving at |v| < c.
- The resultant speed of two velocities with magnitude less than c is always a velocity with magnitude less than c.
- If both |u| and |v| (and then also |u′| and |v′|) are small with respect to the speed of light (that is, e.g., |u/c| ≪ 1), then the intuitive Galilean transformations are recovered from the transformation equations for special relativity
- Attaching a frame to a photon (riding a light beam like Einstein considers) requires special treatment of the transformations.
There is nothing special about the x direction in the standard configuration. The above formalism applies to any direction; and three orthogonal directions allow dealing with all directions in space by decomposing the velocity vectors to their components in these directions. See Velocity-addition formula for details.
Thomas rotation
[edit]The composition of two non-collinear Lorentz boosts (i.e., two non-collinear Lorentz transformations, neither of which involve rotation) results in a Lorentz transformation that is not a pure boost but is the composition of a boost and a rotation.
Thomas rotation results from the relativity of simultaneity. In Fig. 4-5a, a rod of length in its rest frame (i.e., having a proper length of ) rises vertically along the y-axis in the ground frame.
In Fig. 4-5b, the same rod is observed from the frame of a rocket moving at speed to the right. If we imagine two clocks situated at the left and right ends of the rod that are synchronized in the frame of the rod, relativity of simultaneity causes the observer in the rocket frame to observe (not see) the clock at the right end of the rod as being advanced in time by and the rod is correspondingly observed as tilted.[32]: 98–99
Unlike second-order relativistic effects such as length contraction or time dilation, this effect becomes quite significant even at fairly low velocities. For example, this can be seen in the spin of moving particles, where Thomas precession is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope, relating the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion.[32]: 169–174
Thomas rotation provides the resolution to the well-known "meter stick and hole paradox".[p 15][32]: 98–99
Causality and prohibition of motion faster than light
[edit]
In Fig. 4-6, the time interval between the events A (the "cause") and B (the "effect") is 'time-like'; that is, there is a frame of reference in which events A and B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames accessible by a Lorentz transformation. It is possible for matter (or information) to travel (below light speed) from the location of A, starting at the time of A, to the location of B, arriving at the time of B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like'; that is, there is a frame of reference in which events A and C occur simultaneously, separated only in space. There are also frames in which A precedes C (as shown) and frames in which C precedes A. But no frames are accessible by a Lorentz transformation, in which events A and C occur at the same location. If it were possible for a cause-and-effect relationship to exist between events A and C, paradoxes of causality would result.
For example, if signals could be sent faster than light, then signals could be sent into the sender's past (observer B in the diagrams).[46][p 16] A variety of causal paradoxes could then be constructed.
Consider the spacetime diagrams in Fig. 4-7. A and B stand alongside a railroad track, when a high-speed train passes by, with C riding in the last car of the train and D riding in the leading car. The world lines of A and B are vertical (ct), distinguishing the stationary position of these observers on the ground, while the world lines of C and D are tilted forwards (ct′), reflecting the rapid motion of the observers C and D stationary in their train, as observed from the ground.
- Fig. 4-7a. The event of "B passing a message to D", as the leading car passes by, is at the origin of D's frame. D sends the message along the train to C in the rear car, using a fictitious "instantaneous communicator". The worldline of this message is the fat red arrow along the axis, which is a line of simultaneity in the primed frames of C and D. In the (unprimed) ground frame the signal arrives earlier than it was sent.
- Fig. 4-7b. The event of "C passing the message to A", who is standing by the railroad tracks, is at the origin of their frames. Now A sends the message along the tracks to B via an "instantaneous communicator". The worldline of this message is the blue fat arrow, along the axis, which is a line of simultaneity for the frames of A and B. As seen from the spacetime diagram, B will receive the message before having sent it out, a violation of causality.[47]
It is not necessary for signals to be instantaneous to violate causality. Even if the signal from D to C were slightly shallower than the axis (and the signal from A to B slightly steeper than the axis), it would still be possible for B to receive his message before he had sent it. By increasing the speed of the train to near light speeds, the and axes can be squeezed very close to the dashed line representing the speed of light. With this modified setup, it can be demonstrated that even signals only slightly faster than the speed of light will result in causality violation.[48]
Therefore, if causality is to be preserved, one of the consequences of special relativity is that no information signal or material object can travel faster than light in vacuum.
This is not to say that all faster than light speeds are impossible. Various trivial situations can be described where some "things" (not actual matter or energy) move faster than light.[49] For example, the location where the beam of a search light hits the bottom of a cloud can move faster than light when the search light is turned rapidly (although this does not violate causality or any other relativistic phenomenon).[50][51]
Optical effects
[edit]Dragging effects
[edit]
In 1850, Hippolyte Fizeau and Léon Foucault independently established that light travels more slowly in water than in air, thus validating a prediction of Fresnel's wave theory of light and invalidating the corresponding prediction of Newton's corpuscular theory.[52] The speed of light was measured in still water. What would be the speed of light in flowing water?
In 1851, Fizeau conducted an experiment to answer this question, a simplified representation of which is illustrated in Fig. 5-1. A beam of light is divided by a beam splitter, and the split beams are passed in opposite directions through a tube of flowing water. They are recombined to form interference fringes, indicating a difference in optical path length, that an observer can view. The experiment demonstrated that dragging of the light by the flowing water caused a displacement of the fringes, showing that the motion of the water had affected the speed of the light.
According to the theories prevailing at the time, light traveling through a moving medium would be a simple sum of its speed through the medium plus the speed of the medium. Contrary to expectation, Fizeau found that although light appeared to be dragged by the water, the magnitude of the dragging was much lower than expected. If is the speed of light in still water, and is the speed of the water, and is the water-borne speed of light in the lab frame with the flow of water adding to or subtracting from the speed of light, then
Fizeau's results, although consistent with Fresnel's earlier hypothesis of partial aether dragging, were extremely disconcerting to physicists of the time. Among other things, the presence of an index of refraction term meant that, since depends on wavelength, the aether must be capable of sustaining different motions at the same time.[note 8] A variety of theoretical explanations were proposed to explain Fresnel's dragging coefficient, that were completely at odds with each other. Even before the Michelson–Morley experiment, Fizeau's experimental results were among a number of observations that created a critical situation in explaining the optics of moving bodies.[53]
From the point of view of special relativity, Fizeau's result is nothing but an approximation to Equation 10, the relativistic formula for composition of velocities.[31]
Relativistic aberration of light
[edit]
Because of the finite speed of light, if the relative motions of a source and receiver include a transverse component, then the direction from which light arrives at the receiver will be displaced from the geometric position in space of the source relative to the receiver. The classical calculation of the displacement takes two forms and makes different predictions depending on whether the receiver, the source, or both are in motion with respect to the medium. (1) If the receiver is in motion, the displacement would be the consequence of the aberration of light. The incident angle of the beam relative to the receiver would be calculable from the vector sum of the receiver's motions and the velocity of the incident light.[54] (2) If the source is in motion, the displacement would be the consequence of light-time correction. The displacement of the apparent position of the source from its geometric position would be the result of the source's motion during the time that its light takes to reach the receiver.[55]
The classical explanation failed experimental test. Since the aberration angle depends on the relationship between the velocity of the receiver and the speed of the incident light, passage of the incident light through a refractive medium should change the aberration angle. In 1810, Arago used this expected phenomenon in a failed attempt to measure the speed of light,[56] and in 1870, George Airy tested the hypothesis using a water-filled telescope, finding that, against expectation, the measured aberration was identical to the aberration measured with an air-filled telescope.[57] A "cumbrous" attempt to explain these results used the hypothesis of partial aether-drag,[58] but was incompatible with the results of the Michelson–Morley experiment, which apparently demanded complete aether-drag.[59]
Assuming inertial frames, the relativistic expression for the aberration of light is applicable to both the receiver moving and source moving cases. A variety of trigonometrically equivalent formulas have been published. Expressed in terms of the variables in Fig. 5-2, these include[31]: 57–60
- OR OR
Relativistic Doppler effect
[edit]Relativistic longitudinal Doppler effect
[edit]The classical Doppler effect depends on whether the source, receiver, or both are in motion with respect to the medium. The relativistic Doppler effect is independent of any medium. Nevertheless, relativistic Doppler shift for the longitudinal case, with source and receiver moving directly towards or away from each other, can be derived as if it were the classical phenomenon, but modified by the addition of a time dilation term, and that is the treatment described here.[60][61]
Assume the receiver and the source are moving away from each other with a relative speed as measured by an observer on the receiver or the source (The sign convention adopted here is that is negative if the receiver and the source are moving towards each other). Assume that the source is stationary in the medium. Thenwhere is the speed of sound.
For light, and with the receiver moving at relativistic speeds, clocks on the receiver are time dilated relative to clocks at the source. The receiver will measure the received frequency to bewhere
- and
- is the Lorentz factor.
An identical expression for relativistic Doppler shift is obtained when performing the analysis in the reference frame of the receiver with a moving source.[62][21]
Transverse Doppler effect
[edit]
The transverse Doppler effect is one of the main novel predictions of the special theory of relativity.
Classically, one might expect that if source and receiver are moving transversely with respect to each other with no longitudinal component to their relative motions, that there should be no Doppler shift in the light arriving at the receiver.
Special relativity predicts otherwise. Fig. 5-3 illustrates two common variants of this scenario. Both variants can be analyzed using simple time dilation arguments.[21] In Fig. 5-3a, the receiver observes light from the source as being blueshifted by a factor of . In Fig. 5-3b, the light is redshifted by the same factor.
Measurement versus visual appearance
[edit]
Time dilation and length contraction are not optical illusions, but genuine effects. Measurements of these effects are not an artifact of Doppler shift, nor are they the result of neglecting to take into account the time it takes light to travel from an event to an observer.
Scientists make a fundamental distinction between measurement or observation on the one hand, versus visual appearance, or what one sees. The measured shape of an object is a hypothetical snapshot of all of the object's points as they exist at a single moment in time. But the visual appearance of an object is affected by the varying lengths of time that light takes to travel from different points on the object to one's eye.

For many years, the distinction between the two had not been generally appreciated, and it had generally been thought that a length contracted object passing by an observer would in fact actually be seen as length contracted. In 1959, James Terrell and Roger Penrose independently pointed out that differential time lag effects in signals reaching the observer from the different parts of a moving object result in a fast moving object's visual appearance being quite different from its measured shape. For example, a receding object would appear contracted, an approaching object would appear elongated, and a passing object would have a skew appearance that has been likened to a rotation.[p 19][p 20][63][64] A sphere in motion retains the circular outline for all speeds, for any distance, and for all view angles, althoughthe surface of the sphere and the images on it will appear distorted.[65][66]

Both Fig. 5-4 and Fig. 5-5 illustrate objects moving transversely to the line of sight. In Fig. 5-4, a cube is viewed from a distance of four times the length of its sides. At high speeds, the sides of the cube that are perpendicular to the direction of motion appear hyperbolic in shape. The cube is actually not rotated. Rather, light from the rear of the cube takes longer to reach one's eyes compared with light from the front, during which time the cube has moved to the right. At high speeds, the sphere in Fig. 5-5 takes on the appearance of a flattened disk tilted up to 45° from the line of sight. If the objects' motions are not strictly transverse but instead include a longitudinal component, exaggerated distortions in perspective may be seen.[67] This illusion has come to be known as Terrell rotation or the Terrell–Penrose effect.[note 9]
Another example where visual appearance is at odds with measurement comes from the observation of apparent superluminal motion in various radio galaxies, BL Lac objects, quasars, and other astronomical objects that eject relativistic-speed jets of matter at narrow angles with respect to the viewer. An apparent optical illusion results giving the appearance of faster than light travel.[68][69][70] In Fig. 5-6, galaxy M87 streams out a high-speed jet of subatomic particles almost directly towards us, but Penrose–Terrell rotation causes the jet to appear to be moving laterally in the same manner that the appearance of the cube in Fig. 5-4 has been stretched out.[71]
Dynamics
[edit]Section Consequences derived from the Lorentz transformation dealt strictly with kinematics, the study of the motion of points, bodies, and systems of bodies without considering the forces that caused the motion. This section discusses masses, forces, energy and so forth, and as such requires consideration of physical effects beyond those encompassed by the Lorentz transformation itself.
Equivalence of mass and energy
[edit]As an object's speed approaches the speed of light from an observer's point of view, its relativistic mass increases thereby making it more and more difficult to accelerate it from within the observer's frame of reference.
The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that, in any reaction, a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy, for E = mc2.
Mass–energy equivalence is a consequence of special relativity. The energy and momentum, which are separate in Newtonian mechanics, form a four-vector in relativity, and this relates the time component (the energy) to the space components (the momentum) in a non-trivial way. For an object at rest, the energy–momentum four-vector is (E/c, 0, 0, 0): it has a time component which is the energy, and three space components which are zero. By changing frames with a Lorentz transformation in the x direction with a small value of the velocity v, the energy momentum four-vector becomes (E/c, Ev/c2, 0, 0). The momentum is equal to the energy multiplied by the velocity divided by c2. As such, the Newtonian mass of an object, which is the ratio of the momentum to the velocity for slow velocities, is equal to E/c2.
The energy and momentum are properties of matter and radiation, and it is impossible to deduce that they form a four-vector just from the two basic postulates of special relativity by themselves, because these do not talk about matter or radiation, they only talk about space and time. The derivation therefore requires some additional physical reasoning. In his 1905 paper, Einstein used the additional principles that Newtonian mechanics should hold for slow velocities, so that there is one energy scalar and one three-vector momentum at slow velocities, and that the conservation law for energy and momentum is exactly true in relativity. Furthermore, he assumed that the energy of light is transformed by the same Doppler-shift factor as its frequency, which he had previously shown to be true based on Maxwell's equations.[p 1] The first of Einstein's papers on this subject was "Does the Inertia of a Body Depend upon its Energy Content?" in 1905.[p 21] Although Einstein's argument in this paper is nearly universally accepted by physicists as correct, even self-evident, many authors over the years have suggested that it is wrong.[72] Other authors suggest that the argument was merely inconclusive because it relied on some implicit assumptions.[73]
Einstein acknowledged the controversy over his derivation in his 1907 survey paper on special relativity. There he notes that it is problematic to rely on Maxwell's equations for the heuristic mass–energy argument. The argument in his 1905 paper can be carried out with the emission of any massless particles, but the Maxwell equations are implicitly used to make it obvious that the emission of light in particular can be achieved only by doing work. To emit electromagnetic waves, all you have to do is shake a charged particle, and this is clearly doing work, so that the emission is of energy.[p 22][note 10]
Einstein's 1905 demonstration of E = mc2
[edit]In his fourth of his 1905 Annus mirabilis papers,[p 21] Einstein presented a heuristic argument for the equivalence of mass and energy. Although, as discussed above, subsequent scholarship has established that his arguments fell short of a broadly definitive proof, the conclusions that he reached in this paper have stood the test of time.
Einstein took as starting assumptions his recently discovered formula for relativistic Doppler shift, the laws of conservation of energy and conservation of momentum, and the relationship between the frequency of light and its energy as implied by Maxwell's equations.
Fig. 6-1 (top). Consider a system of plane waves of light having frequency traveling in direction relative to the x-axis of reference frame S. The frequency (and hence energy) of the waves as measured in frame S′ that is moving along the x-axis at velocity is given by the relativistic Doppler shift formula which Einstein had developed in his 1905 paper on special relativity:[p 1]
Fig. 6-1 (bottom). Consider an arbitrary body that is stationary in reference frame S. Let this body emit a pair of equal-energy light-pulses in opposite directions at angle with respect to the x-axis. Each pulse has energy . Because of conservation of momentum, the body remains stationary in S after emission of the two pulses. Let be the energy of the body before emission of the two pulses and after their emission.
Next, consider the same system observed from frame S′ that is moving along the x-axis at speed relative to frame S. In this frame, light from the forwards and reverse pulses will be relativistically Doppler-shifted. Let be the energy of the body measured in reference frame S′ before emission of the two pulses and after their emission. We obtain the following relationships:[p 21]
From the above equations, we obtain the following:
| (6-1) |
The two differences of form seen in the above equation have a straightforward physical interpretation. Since and are the energies of the arbitrary body in the moving and stationary frames, and represents the kinetic energies of the bodies before and after the emission of light (except for an additive constant that fixes the zero point of energy and is conventionally set to zero). Hence,
| (6-2) |
Taking a Taylor series expansion and neglecting higher order terms, he obtained
| (6-3) |
Comparing the above expression with the classical expression for kinetic energy, K.E. = 1/2mv2, Einstein then noted: "If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2."
Rindler has observed that Einstein's heuristic argument suggested merely that energy contributes to mass. In 1905, Einstein's cautious expression of the mass–energy relationship allowed for the possibility that "dormant" mass might exist that would remain behind after all the energy of a body was removed. By 1907, however, Einstein was ready to assert that all inertial mass represented a reserve of energy. "To equate all mass with energy required an act of aesthetic faith, very characteristic of Einstein."[12]: 81–84 Einstein's bold hypothesis has been amply confirmed in the years subsequent to his original proposal.
For a variety of reasons, Einstein's original derivation is currently seldom taught. Besides the vigorous debate that continues until this day as to the formal correctness of his original derivation, the recognition of special relativity as being what Einstein called a "principle theory" has led to a shift away from reliance on electromagnetic phenomena to purely dynamic methods of proof.[74]
How far can you travel from the Earth?
[edit]Since nothing can travel faster than light, one might conclude that a human can never travel farther from Earth than ~100 light years. You would easily think that a traveler would never be able to reach more than the few solar systems which exist within the limit of 100 light years from Earth. However, because of time dilation, a hypothetical spaceship can travel thousands of light years during a passenger's lifetime. If a spaceship could be built that accelerates at a constant 1g, it will, after one year, be travelling at almost the speed of light as seen from Earth. This is described by:where v(t) is the velocity at a time t, a is the acceleration of the spaceship and t is the coordinate time as measured by people on Earth.[p 23] Therefore, after one year of accelerating at 9.81 m/s2, the spaceship will be travelling at v = 0.712c and 0.946c after three years, relative to Earth. After three years of this acceleration, with the spaceship achieving a velocity of 94.6% of the speed of light relative to Earth, time dilation will result in each second experienced on the spaceship corresponding to 3.1 seconds back on Earth. During their journey, people on Earth will experience more time than they do - since their clocks (all physical phenomena) would really be ticking 3.1 times faster than those of the spaceship. A 5-year round trip for the traveller will take 6.5 Earth years and cover a distance of over 6 light-years. A 20-year round trip for them (5 years accelerating, 5 decelerating, twice each) will land them back on Earth having travelled for 335 Earth years and a distance of 331 light years.[75] A full 40-year trip at 1g will appear on Earth to last 58,000 years and cover a distance of 55,000 light years. A 40-year trip at 1.1g will take 148,000 Earth years and cover about 140,000 light years. A one-way 28 year (14 years accelerating, 14 decelerating as measured with the astronaut's clock) trip at 1g acceleration could reach 2,000,000 light-years to the Andromeda Galaxy.[75] This same time dilation is why a muon travelling close to c is observed to travel much farther than c times its half-life (when at rest).[76]
Elastic collisions
[edit]Examination of the collision products generated by particle accelerators around the world provides scientists evidence of the structure of the subatomic world and the natural laws governing it. Analysis of the collision products, the sum of whose masses may vastly exceed the masses of the incident particles, requires special relativity.[77]
In Newtonian mechanics, analysis of collisions involves use of the conservation laws for mass, momentum and energy. In relativistic mechanics, mass is not independently conserved, because it has been subsumed into the total relativistic energy. We illustrate the differences that arise between the Newtonian and relativistic treatments of particle collisions by examining the simple case of two perfectly elastic colliding particles of equal mass. (Inelastic collisions are discussed in Spacetime#Conservation laws. Radioactive decay may be considered a sort of time-reversed inelastic collision.[77])
Elastic scattering of charged elementary particles deviates from ideality due to the production of Bremsstrahlung radiation.[78][79]
Newtonian analysis
[edit]
Fig. 6-2 provides a demonstration of the result, familiar to billiard players, that if a stationary ball is struck elastically by another one of the same mass (assuming no sidespin, or "English"), then after collision, the diverging paths of the two balls will subtend a right angle. (a) In the stationary frame, an incident sphere traveling at 2v strikes a stationary sphere. (b) In the center of momentum frame, the two spheres approach each other symmetrically at ±v. After elastic collision, the two spheres rebound from each other with equal and opposite velocities ±u. Energy conservation requires that |u| = |v|. (c) Reverting to the stationary frame, the rebound velocities are v ± u. The dot product (v + u) ⋅ (v − u) = v2 − u2 = 0, indicating that the vectors are orthogonal.[12]: 26–27
Relativistic analysis
[edit]
Consider the elastic collision scenario in Fig. 6-3 between a moving particle colliding with an equal mass stationary particle. Unlike the Newtonian case, the angle between the two particles after collision is less than 90°, is dependent on the angle of scattering, and becomes smaller and smaller as the velocity of the incident particle approaches the speed of light:
The relativistic momentum and total relativistic energy of a particle are given by
| (6-4) |
Conservation of momentum dictates that the sum of the momenta of the incoming particle and the stationary particle (which initially has momentum = 0) equals the sum of the momenta of the emergent particles:
| (6-5) |
Likewise, the sum of the total relativistic energies of the incoming particle and the stationary particle (which initially has total energy mc2) equals the sum of the total energies of the emergent particles:
| (6-6) |
Breaking down (6-5) into its components, replacing with the dimensionless , and factoring out common terms from (6-5) and (6-6) yields the following:[p 24]
| (6-7) |
| (6-8) |
| (6-9) |
From these we obtain the following relationships:[p 24]
| (6-10) |
| (6-11) |
| (6-12) |
For the symmetrical case in which and (6-12) takes on the simpler form:[p 24]
| (6-13) |
Beyond the basics
[edit]Rapidity
[edit]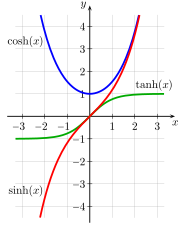
Lorentz transformations relate coordinates of events in one reference frame to those of another frame. Relativistic composition of velocities is used to add two velocities together. The formulas to perform the latter computations are nonlinear, making them more complex than the corresponding Galilean formulas.
This nonlinearity is an artifact of our choice of parameters.[80]: 47–59 We have previously noted that in an x–ct spacetime diagram, the points at some constant spacetime interval from the origin form an invariant hyperbola. We have also noted that the coordinate systems of two spacetime reference frames in standard configuration are hyperbolically rotated with respect to each other.
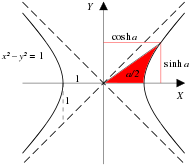
The natural functions for expressing these relationships are the hyperbolic analogs of the trigonometric functions. Fig. 7-1a shows a unit circle with sin(a) and cos(a), the only difference between this diagram and the familiar unit circle of elementary trigonometry being that a is interpreted, not as the angle between the ray and the x-axis, but as twice the area of the sector swept out by the ray from the x-axis. Numerically, the angle and 2 × area measures for the unit circle are identical. Fig. 7-1b shows a unit hyperbola with sinh(a) and cosh(a), where a is likewise interpreted as twice the tinted area.[81] Fig. 7-2 presents plots of the sinh, cosh, and tanh functions.
For the unit circle, the slope of the ray is given by
In the Cartesian plane, rotation of point (x, y) into point (x', y') by angle θ is given by
In a spacetime diagram, the velocity parameter is the analog of slope. The rapidity, φ, is defined by[21]: 96–99
where
The rapidity defined above is very useful in special relativity because many expressions take on a considerably simpler form when expressed in terms of it. For example, rapidity is simply additive in the collinear velocity-addition formula;[80]: 47–59
or in other words,
The Lorentz transformations take a simple form when expressed in terms of rapidity. The γ factor can be written as
Transformations describing relative motion with uniform velocity and without rotation of the space coordinate axes are called boosts.
Substituting γ and γβ into the transformations as previously presented and rewriting in matrix form, the Lorentz boost in the x-direction may be written as
and the inverse Lorentz boost in the x-direction may be written as
In other words, Lorentz boosts represent hyperbolic rotations in Minkowski spacetime.[21]: 96–99
The advantages of using hyperbolic functions are such that some textbooks such as the classic ones by Taylor and Wheeler introduce their use at a very early stage.[80][82][note 11]
4‑vectors
[edit]Four‑vectors have been mentioned above in context of the energy–momentum 4‑vector, but without any great emphasis. Indeed, none of the elementary derivations of special relativity require them. But once understood, 4‑vectors, and more generally tensors, greatly simplify the mathematics and conceptual understanding of special relativity. Working exclusively with such objects leads to formulas that are manifestly relativistically invariant, which is a considerable advantage in non-trivial contexts. For instance, demonstrating relativistic invariance of Maxwell's equations in their usual form is not trivial, while it is merely a routine calculation, really no more than an observation, using the field strength tensor formulation.[83]
On the other hand, general relativity, from the outset, relies heavily on 4‑vectors, and more generally tensors, representing physically relevant entities. Relating these via equations that do not rely on specific coordinates requires tensors, capable of connecting such 4‑vectors even within a curved spacetime, and not just within a flat one as in special relativity. The study of tensors is outside the scope of this article, which provides only a basic discussion of spacetime.
Definition of 4-vectors
[edit]A 4-tuple, is a "4-vector" if its component Ai transform between frames according to the Lorentz transformation.
If using coordinates, A is a 4–vector if it transforms (in the x-direction) according to
which comes from simply replacing ct with A0 and x with A1 in the earlier presentation of the Lorentz transformation.
As usual, when we write x, t, etc. we generally mean Δx, Δt etc.
The last three components of a 4–vector must be a standard vector in three-dimensional space. Therefore, a 4–vector must transform like under Lorentz transformations as well as rotations.[84]: 36–59
Properties of 4-vectors
[edit]- Closure under linear combination: If A and B are 4-vectors, then is also a 4-vector.
- Inner-product invariance: If A and B are 4-vectors, then their inner product (scalar product) is invariant, i.e. their inner product is independent of the frame in which it is calculated. Note how the calculation of inner product differs from the calculation of the inner product of a 3-vector. In the following, and are 3-vectors:
- In addition to being invariant under Lorentz transformation, the above inner product is also invariant under rotation in 3-space.
- Two vectors are said to be orthogonal if Unlike the case with 3-vectors, orthogonal 4-vectors are not necessarily at right angles with each other. The rule is that two 4-vectors are orthogonal if they are offset by equal and opposite angles from the 45° line which is the world line of a light ray. This implies that a lightlike 4-vector is orthogonal with itself.
- Invariance of the magnitude of a vector: The magnitude of a vector is the inner product of a 4-vector with itself, and is a frame-independent property. As with intervals, the magnitude may be positive, negative or zero, so that the vectors are referred to as timelike, spacelike or null (lightlike). Note that a null vector is not the same as a zero vector. A null vector is one for which while a zero vector is one whose components are all zero. Special cases illustrating the invariance of the norm include the invariant interval and the invariant length of the relativistic momentum vector [21]: 178–181 [84]: 36–59
Examples of 4-vectors
[edit]- Displacement 4-vector: Otherwise known as the spacetime separation, this is (Δt, Δx, Δy, Δz), or for infinitesimal separations, (dt, dx, dy, dz).
- Velocity 4-vector: This results when the displacement 4-vector is divided by , where is the proper time between the two events that yield dt, dx, dy, and dz.
- The 4-velocity is tangent to the world line of a particle, and has a length equal to one unit of time in the frame of the particle.
- An accelerated particle does not have an inertial frame in which it is always at rest. However, an inertial frame can always be found which is momentarily comoving with the particle. This frame, the momentarily comoving reference frame (MCRF), enables application of special relativity to the analysis of accelerated particles.
- Since photons move on null lines, for a photon, and a 4-velocity cannot be defined. There is no frame in which a photon is at rest, and no MCRF can be established along a photon's path.
- Energy–momentum 4-vector:
- As indicated before, there are varying treatments for the energy-momentum 4-vector so that one may also see it expressed as or The first component is the total energy (including mass) of the particle (or system of particles) in a given frame, while the remaining components are its spatial momentum. The energy-momentum 4-vector is a conserved quantity.
- Acceleration 4-vector: This results from taking the derivative of the velocity 4-vector with respect to
- Force 4-vector: This is the derivative of the momentum 4-vector with respect to
As expected, the final components of the above 4-vectors are all standard 3-vectors corresponding to spatial 3-momentum, 3-force etc.[21]: 178–181 [84]: 36–59
4-vectors and physical law
[edit]The first postulate of special relativity declares the equivalency of all inertial frames. A physical law holding in one frame must apply in all frames, since otherwise it would be possible to differentiate between frames. Newtonian momenta fail to behave properly under Lorentzian transformation, and Einstein preferred to change the definition of momentum to one involving 4-vectors rather than give up on conservation of momentum.
Physical laws must be based on constructs that are frame independent. This means that physical laws may take the form of equations connecting scalars, which are always frame independent. However, equations involving 4-vectors require the use of tensors with appropriate rank, which themselves can be thought of as being built up from 4-vectors.[21]: 186
Acceleration
[edit]It is a common misconception that special relativity is applicable only to inertial frames, and that it is unable to handle accelerating objects or accelerating reference frames. Actually, accelerating objects can generally be analyzed without needing to deal with accelerating frames at all. It is only when gravitation is significant that general relativity is required.[85]
Properly handling accelerating frames does require some care, however. The difference between special and general relativity is that (1) In special relativity, all velocities are relative, but acceleration is absolute. (2) In general relativity, all motion is relative, whether inertial, accelerating, or rotating. To accommodate this difference, general relativity uses curved spacetime.[85]
In this section, we analyze several scenarios involving accelerated reference frames.
Dewan–Beran–Bell spaceship paradox
[edit]The Dewan–Beran–Bell spaceship paradox (Bell's spaceship paradox) is a good example of a problem where intuitive reasoning unassisted by the geometric insight of the spacetime approach can lead to issues.

In Fig. 7-4, two identical spaceships float in space and are at rest relative to each other. They are connected by a string which is capable of only a limited amount of stretching before breaking. At a given instant in our frame, the observer frame, both spaceships accelerate in the same direction along the line between them with the same constant proper acceleration.[note 12] Will the string break?
When the paradox was new and relatively unknown, even professional physicists had difficulty working out the solution. Two lines of reasoning lead to opposite conclusions. Both arguments, which are presented below, are flawed even though one of them yields the correct answer.[21]: 106, 120–122
- To observers in the rest frame, the spaceships start a distance L apart and remain the same distance apart during acceleration. During acceleration, L is a length contracted distance of the distance L' = γL in the frame of the accelerating spaceships. After a sufficiently long time, γ will increase to a sufficiently large factor that the string must break.
- Let A and B be the rear and front spaceships. In the frame of the spaceships, each spaceship sees the other spaceship doing the same thing that it is doing. A says that B has the same acceleration that he has, and B sees that A matches her every move. So the spaceships stay the same distance apart, and the string does not break.[21]: 106, 120–122
The problem with the first argument is that there is no "frame of the spaceships." There cannot be, because the two spaceships measure a growing distance between the two. Because there is no common frame of the spaceships, the length of the string is ill-defined. Nevertheless, the conclusion is correct, and the argument is mostly right. The second argument, however, completely ignores the relativity of simultaneity.[21]: 106, 120–122
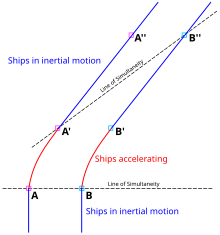
A spacetime diagram (Fig. 7-5) makes the correct solution to this paradox almost immediately evident. Two observers in Minkowski spacetime accelerate with constant magnitude acceleration for proper time (acceleration and elapsed time measured by the observers themselves, not some inertial observer). They are comoving and inertial before and after this phase. In Minkowski geometry, the length along the line of simultaneity turns out to be greater than the length along the line of simultaneity .
The length increase can be calculated with the help of the Lorentz transformation. If, as illustrated in Fig. 7-5, the acceleration is finished, the ships will remain at a constant offset in some frame If and are the ships' positions in the positions in frame are:[86]
The "paradox", as it were, comes from the way that Bell constructed his example. In the usual discussion of Lorentz contraction, the rest length is fixed and the moving length shortens as measured in frame . As shown in Fig. 7-5, Bell's example asserts the moving lengths and measured in frame to be fixed, thereby forcing the rest frame length in frame to increase.
Accelerated observer with horizon
[edit]Certain special relativity problem setups can lead to insight about phenomena normally associated with general relativity, such as event horizons. In the text accompanying Section "Invariant hyperbola" of the article Spacetime, the magenta hyperbolae represented actual paths that are tracked by a constantly accelerating traveler in spacetime. During periods of positive acceleration, the traveler's velocity just approaches the speed of light, while, measured in our frame, the traveler's acceleration constantly decreases.
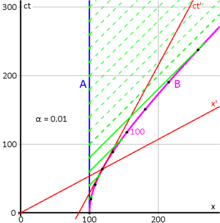
Fig. 7-6 details various features of the traveler's motions with more specificity. At any given moment, her space axis is formed by a line passing through the origin and her current position on the hyperbola, while her time axis is the tangent to the hyperbola at her position. The velocity parameter approaches a limit of one as increases. Likewise, approaches infinity.
The shape of the invariant hyperbola corresponds to a path of constant proper acceleration. This is demonstrable as follows:
- We remember that
- Since we conclude that
- From the relativistic force law,
- Substituting from step 2 and the expression for from step 3 yields which is a constant expression.[87]: 110–113
Fig. 7-6 illustrates a specific calculated scenario. Terence (A) and Stella (B) initially stand together 100 light hours from the origin. Stella lifts off at time 0, her spacecraft accelerating at 0.01 c per hour. Every twenty hours, Terence radios updates to Stella about the situation at home (solid green lines). Stella receives these regular transmissions, but the increasing distance (offset in part by time dilation) causes her to receive Terence's communications later and later as measured on her clock, and she never receives any communications from Terence after 100 hours on his clock (dashed green lines).[87]: 110–113
After 100 hours according to Terence's clock, Stella enters a dark region. She has traveled outside Terence's timelike future. On the other hand, Terence can continue to receive Stella's messages to him indefinitely. He just has to wait long enough. Spacetime has been divided into distinct regions separated by an apparent event horizon. So long as Stella continues to accelerate, she can never know what takes place behind this horizon.[87]: 110–113
Relativity and unifying electromagnetism
[edit]Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic field. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Maxwell's equations in the 3D form are already consistent with the physical content of special relativity, although they are easier to manipulate in a manifestly covariant form, that is, in the language of tensor calculus.[83]
Theories of relativity and quantum mechanics
[edit]Special relativity can be combined with quantum mechanics to form relativistic quantum mechanics and quantum electrodynamics. How general relativity and quantum mechanics can be unified is one of the unsolved problems in physics; quantum gravity and a "theory of everything", which require a unification including general relativity too, are active and ongoing areas in theoretical research.
The early Bohr–Sommerfeld atomic model explained the fine structure of alkali metal atoms using both special relativity and the preliminary knowledge on quantum mechanics of the time.[88]
In 1928, Paul Dirac constructed an influential relativistic wave equation, now known as the Dirac equation in his honour,[p 25] that is fully compatible both with special relativity and with the final version of quantum theory existing after 1926. This equation not only described the intrinsic angular momentum of the electrons called spin, it also led to the prediction of the antiparticle of the electron (the positron),[p 25][p 26] and fine structure could only be fully explained with special relativity. It was the first foundation of relativistic quantum mechanics.
On the other hand, the existence of antiparticles leads to the conclusion that relativistic quantum mechanics is not enough for a more accurate and complete theory of particle interactions. Instead, a theory of particles interpreted as quantized fields, called quantum field theory, becomes necessary; in which particles can be created and destroyed throughout space and time.
Status
[edit]Special relativity in its Minkowski spacetime is accurate only when the absolute value of the gravitational potential is much less than c2 in the region of interest.[89] In a strong gravitational field, one must use general relativity. General relativity becomes special relativity at the limit of a weak field. At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravity. But at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10−20)[90]and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.[91]
Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) – thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See classical mechanics for a more detailed discussion.
Several experiments predating Einstein's 1905 paper are now interpreted as evidence for relativity. Of these it is known Einstein was aware of the Fizeau experiment before 1905,[92] and historians have concluded that Einstein was at least aware of the Michelson–Morley experiment as early as 1899 despite claims he made in his later years that it played no role in his development of the theory.[16]
- The Fizeau experiment (1851, repeated by Michelson and Morley in 1886) measured the speed of light in moving media, with results that are consistent with relativistic addition of colinear velocities.
- The famous Michelson–Morley experiment (1881, 1887) gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
- The Trouton–Noble experiment (1903) showed that the torque on a capacitor is independent of position and inertial reference frame.
- The Experiments of Rayleigh and Brace (1902, 1904) showed that length contraction does not lead to birefringence for a co-moving observer, in accordance with the relativity principle.
Particle accelerators accelerate and measure the properties of particles moving at near the speed of light, where their behavior is consistent with relativity theory and inconsistent with the earlier Newtonian mechanics. These machines would simply not work if they were not engineered according to relativistic principles. In addition, a considerable number of modern experiments have been conducted to test special relativity. Some examples:
- Tests of relativistic energy and momentum – testing the limiting speed of particles
- Ives–Stilwell experiment – testing relativistic Doppler effect and time dilation
- Experimental testing of time dilation – relativistic effects on a fast-moving particle's half-life
- Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Hughes–Drever experiment – testing isotropy of space and mass
- Modern searches for Lorentz violation – various modern tests
- Experiments to test emission theory demonstrated that the speed of light is independent of the speed of the emitter.
- Experiments to test the aether drag hypothesis – no "aether flow obstruction".
Technical discussion of spacetime
[edit]Geometry of spacetime
[edit]Comparison between flat Euclidean space and Minkowski space
[edit]
Special relativity uses a "flat" 4-dimensional Minkowski space – an example of a spacetime. Minkowski spacetime appears to be very similar to the standard 3-dimensional Euclidean space, but there is a crucial difference with respect to time.
In 3D space, the differential of distance (line element) ds is defined bywhere dx = (dx1, dx2, dx3) are the differentials of the three spatial dimensions. In Minkowski geometry, there is an extra dimension with coordinate X0 derived from time, such that the distance differential fulfillswhere dX = (dX0, dX1, dX2, dX3) are the differentials of the four spacetime dimensions. This suggests a deep theoretical insight: special relativity is simply a rotational symmetry of our spacetime, analogous to the rotational symmetry of Euclidean space (see Fig. 10-1).[94] Just as Euclidean space uses a Euclidean metric, so spacetime uses a Minkowski metric. Basically, special relativity can be stated as the invariance of any spacetime interval (that is the 4D distance between any two events) when viewed from any inertial reference frame. All equations and effects of special relativity can be derived from this rotational symmetry (the Poincaré group) of Minkowski spacetime.
The actual form of ds above depends on the metric and on the choices for the X0 coordinate.To make the time coordinate look like the space coordinates, it can be treated as imaginary: X0 = ict (this is called a Wick rotation).According to Misner, Thorne and Wheeler (1971, §2.3), ultimately the deeper understanding of both special and general relativity will come from the study of the Minkowski metric (described below) and to take X0 = ct, rather than a "disguised" Euclidean metric using ict as the time coordinate.
Some authors use X0 = t, with factors of c elsewhere to compensate; for instance, spatial coordinates are divided by c or factors of c±2 are included in the metric tensor.[95]These numerous conventions can be superseded by using natural units where c = 1. Then space and time have equivalent units, and no factors of c appear anywhere.
3D spacetime
[edit]
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3D spacewe see that the null geodesics lie along a dual-cone (see Fig. 10-2) defined by the equation;or simplywhich is the equation of a circle of radius c dt.
4D spacetime
[edit]If we extend this to three spatial dimensions, the null geodesics are the 4-dimensional cone:so

As illustrated in Fig. 10-3, the null geodesics can be visualized as a set of continuous concentric spheres with radii = c dt.
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old", we are looking down this line of sight: a null geodesic. We are looking at an event a distance away and a time d/c in the past. For this reason the null dual cone is also known as the "light cone". (The point in the lower left of the Fig. 10-2 represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the −t region is the information that the point is "receiving", while the cone in the +t section is the information that the point is "sending".
Геометрию пространства Минковского можно изобразить с помощью диаграмм Минковского , которые также полезны для понимания многих мысленных экспериментов в специальной теории относительности.
Физика в пространстве-времени
[ редактировать ]Преобразования физических величин между системами отсчета
[ редактировать ]Выше преобразование Лоренца для временной координаты и трех пространственных координат показывает, что они переплетаются. Это верно в более общем плане: определенные пары «времяподобных» и «пространственноподобных» величин естественным образом объединяются на равных основаниях при одном и том же преобразовании Лоренца.
Преобразование Лоренца в стандартной конфигурации, указанной выше, то есть для повышения в направлении x , можно преобразовать в матричную форму следующим образом:
В ньютоновской механике величины, имеющие величину и направление, математически описываются как трехмерные векторы в евклидовом пространстве и, как правило, параметризуются временем. В специальной теории относительности это понятие расширяется за счет добавления соответствующей времениподобной величины к пространственноподобной векторной величине, и мы получаем 4D-векторы, или « четыре-векторы », в пространстве-времени Минковского. Компоненты векторов записываются с использованием тензорной индексной нотации , поскольку это имеет множество преимуществ. Обозначения проясняют, что уравнения явно ковариантны относительно группы Пуанкаре , что позволяет избежать утомительных вычислений для проверки этого факта. При построении таких уравнений мы часто обнаруживаем, что уравнения, которые раньше считались несвязанными, на самом деле тесно связаны, являясь частью одного и того же тензорного уравнения. других физических величин тензорами Признание упрощает законы их преобразования. Всюду верхние индексы (верхние индексы) являются контравариантными индексами, а не экспонентами, за исключением случаев, когда они обозначают квадрат (это должно быть ясно из контекста), а нижние индексы (нижние индексы) являются ковариантными индексами. Для простоты и согласованности с предыдущими уравнениями будут использоваться декартовы координаты.
Простейшим примером четырехвектора является положение события в пространстве-времени, которое представляет собой времяподобный компонент ct и пространственноподобный компонент x = ( x , y , z ) в контравариантном положения четырехвекторе с компонентами: где мы определяем X 0 = ct , чтобы временная координата имела ту же размерность расстояния, что и другие пространственные измерения; так что пространство и время рассматриваются одинаково. [96] [97] [98] Теперь преобразование контравариантных компонент позиционного 4-вектора можно компактно записать как: где имеется подразумеваемое суммирование по от 0 до 3, и является матрицей .
В более общем смысле, все контравариантные компоненты четырехвектора преобразовать один кадр в другой с помощью преобразования Лоренца :
Примеры других 4-векторов включают четырехскоростной определяется как производная 4-вектора положения по собственному времени : где фактор Лоренца:
Релятивистская энергия и релятивистский импульс объекта являются соответственно времениподобными и пространственноподобными компонентами контравариантного вектора четырехимпульса : где m — инвариантная масса .
Четырех -ускорение является собственной производной по времени от 4-скорости:
Правила преобразования трехмерных скоростей и ускорений очень неудобны; даже выше в стандартной конфигурации уравнения скорости весьма сложны из-за своей нелинейности. С другой стороны, преобразование четырех скоростей и четырех ускорений проще с помощью матрицы преобразования Лоренца.
Четырехградиент φ преобразуется ковариантно , скалярного поля а не контравариантно: что является транспонированием: только в декартовых координатах. Именно ковариантная производная преобразуется в явную ковариацию, в декартовых координатах это сводится к частным производным, но не в других координатах.
В более общем смысле, ковариантные компоненты 4-векторного преобразования согласно обратному преобразованию Лоренца: где является обратной матрицей .
Постулаты специальной теории относительности ограничивают точную форму, которую принимают матрицы преобразования Лоренца.
(компоненты) В более общем смысле, большинство физических величин лучше всего описать как тензоры . Итак, для преобразования из одного кадра в другой мы используем известный закон тензорного преобразования. [99] где является обратной матрицей . Все тензоры преобразуются по этому правилу.
Примером четырехмерного антисимметричного тензора второго порядка является релятивистский угловой момент , который имеет шесть компонентов: три — классический угловой момент , а остальные три связаны с усилением центра масс системы. Производная релятивистского углового момента по собственному времени — это релятивистский крутящий момент, также антисимметричный тензор второго порядка .
Тензор электромагнитного поля второго порядка — это еще один антисимметричный тензор с шестью компонентами: три для электрического поля и еще три для магнитного поля . Существует также тензор энергии-импульса для электромагнитного поля, а именно электромагнитный тензор энергии-напряжения .
Метрика
[ редактировать ]Метрический тензор позволяет определить скалярное произведение двух векторов, что, в свою очередь, позволяет присвоить вектору величину. Учитывая четырехмерную природу пространства-времени, метрика Минковского η имеет компоненты (действительные с правильно выбранными координатами), которые можно расположить в матрице 4 × 4 : который равен своему обратному значению, , в этих кадрах. Повсюду мы используем знаки, указанные выше, разные авторы используют разные соглашения - см. метрики Минковского Альтернативные знаки .
Группа Пуанкаре — наиболее общая группа преобразований, сохраняющая метрику Минковского: и это физическая симметрия, лежащая в основе специальной теории относительности.
Метрику можно использовать для повышения и понижения индексов векторов и тензоров. Инварианты могут быть построены с использованием метрики, скалярное произведение 4-вектора T с другим 4-вектором S равно:
Инвариант означает, что он принимает одно и то же значение во всех инерциальных системах отсчета, поскольку он является скаляром (тензор ранга 0), и поэтому Λ в его тривиальном преобразовании не появляется . Величина 4-вектора T представляет собой положительный квадратный корень из внутреннего произведения самого себя:
Эту идею можно распространить на тензоры более высокого порядка, для тензора второго порядка можно сформировать инварианты: аналогично для тензоров более высокого порядка. Инвариантные выражения, особенно внутренние произведения 4-векторов сами на себя, дают уравнения, полезные для вычислений, поскольку для определения инвариантов не нужно выполнять преобразования Лоренца.
Релятивистская кинематика и инвариантность
[ редактировать ]Координатные дифференциалы преобразуются также контрвариантно: поэтому квадрат длины дифференциала позиционного четырехвектора dX м построен с использованием является инвариантом. Обратите внимание, что когда элемент линии d X 2 отрицательно, что √ − d X 2 – дифференциал собственного времени , а при d X 2 положительно, √ d X 2 является дифференциалом собственного расстояния .
4-скоростной U м имеет инвариантную форму: это означает, что все четыре вектора скорости имеют величину c . Это выражение того факта, что в теории относительности не существует такого понятия, как координатный покой: по крайней мере, вы всегда движетесь вперед во времени. Дифференцирование приведенного выше уравнения по τ дает: Таким образом, в специальной теории относительности четырехвектор ускорения и четырехвектор скорости ортогональны.
Релятивистская динамика и инвариантность
[ редактировать ]Инвариантная величина 4-вектора импульса порождает соотношение энергия-импульс :
Мы можем выяснить, что представляет собой этот инвариант, сначала доказав, что, поскольку он является скаляром, не имеет значения, в какой системе отсчета мы его вычисляем, а затем преобразуя его в систему отсчета, в которой полный импульс равен нулю.
Мы видим, что энергия покоя является независимым инвариантом. Энергию покоя можно вычислить даже для частиц и систем, находящихся в движении, путем перевода в систему отсчета, в которой импульс равен нулю.
Оставшаяся энергия связана с массой согласно знаменитому уравнению, обсуждавшемуся выше:
Масса систем, измеренная в их центре системы импульса (где общий импульс равен нулю), определяется полной энергией системы в этой системе отсчета. Она может не быть равна сумме масс отдельных систем, измеренных в других системах отсчета.
Чтобы использовать третий закон движения Ньютона , обе силы должны быть определены как скорость изменения импульса относительно одной и той же временной координаты. То есть для этого требуется 3D-сила, определенная выше. К сожалению, в 4D нет тензора, который среди своих компонент содержал бы компоненты вектора 3D силы.
Если частица не движется в точке c , можно преобразовать трехмерную силу из сопутствующей системы отсчета частицы в систему отсчета наблюдателя. Это дает 4-вектор, называемый четырехсилой . Это скорость изменения указанного выше четырехвектора энергии - импульса относительно собственного времени. Ковариантная версия четырех сил:
В системе покоя объекта временная составляющая четырех сил равна нулю, если только « инвариантная масса » объекта не меняется (для этого требуется незамкнутая система, в которой энергия/масса напрямую добавляется или удаляется из системы). объекта), и в этом случае это отрицательное значение скорости изменения массы, умноженное на c . Однако в целом компоненты четырехсилы не равны компонентам трехсилы, поскольку трехсила определяется скоростью изменения импульса по отношению к координатному времени, то есть dp / dt, в то время как четырехсила определяется скоростью изменения импульса по отношению к собственному времени, то есть dp / dτ .
В сплошной среде трехмерная плотность силы объединяется с плотностью мощности, образуя ковариантный 4-вектор. Пространственная часть является результатом деления силы, действующей на маленькую ячейку (в трехмерном пространстве) на объем этой ячейки. Временная составляющая равна -1/ c, умноженной на мощность, передаваемую в эту ячейку, деленную на объем ячейки. Это будет использоваться ниже в разделе, посвященном электромагнетизму.
См. также
[ редактировать ]- Люди
- относительность
- История специальной теории относительности
- Двойная специальная теория относительности
- Бонди k-исчисление
- Синхронизация Эйнштейна
- Аргумент Ритдейка-Патнэма
- Специальная теория относительности (альтернативные формулировки)
- Спор о приоритете теории относительности
- Физика
- Мысленные эксперименты Эйнштейна
- физическая космология
- Релятивистские уравнения Эйлера
- Теория эфира Лоренца
- Проблема с движущимся магнитом и проводником
- Форма волн
- Релятивистская теплопроводность
- Релятивистский диск
- Прирожденная жесткость
- Координаты рождения
- Математика
- Философия
- Парадоксы
- Эренфест парадоксальный
- Парадокс космического корабля Белла
- Парадокс скоростной композиции
- Парадокс маяка
Примечания
[ редактировать ]- ^ Сам Эйнштейн, в «Основах общей теории относительности», Ann. Физ. 49 (1916) пишет: «Слово «специальный» означает, что принцип ограничен случаем…». См. стр. 111 «Принципа относительности», А. Эйнштейн, Х. А. Лоренц, Х. Вейль, Х. Минковский, Дуврское переиздание перевода Метуэна и компании 1923 года.]
- ^ Уолд, Общая теория относительности, с. 60: «...специальная теория относительности утверждает, что пространство-время — это многообразие с определенной на ней плоской метрикой сигнатуры Лоренца. И наоборот, все содержание специальной теории относительности... содержится в этом утверждении..."
- ^ В пространстве-времени длина движущегося твердого объекта — это пространственное расстояние между концами объекта, измеренное одновременно. В остальном кадре объекта одновременность не требуется.
- ^ Результаты эксперимента Майкельсона-Морли побудили Джорджа Фрэнсиса Фитцджеральда и Хендрика Лоренца независимо предложить явление сокращения длины . Лоренц считал, что сокращение длины представляет собой физическое сжатие атомов, составляющих объект. Он не предполагал никаких фундаментальных изменений в природе пространства и времени. [28] : 62–68
Лоренц ожидал, что сокращение длины приведет к сжимающим деформациям объекта, что должно привести к измеримым эффектам. К таким эффектам относятся оптические эффекты в прозрачных средах, такие как оптическое вращение. [стр. 11] и индукция двойного лучепреломления, [стр. 12] и индукция крутящих моментов на заряженных конденсаторах, движущихся под углом к эфиру. [стр. 12] Лоренц был озадачен такими экспериментами, как эксперимент Траутона-Нобла и экспериментами Рэлея и Брейса , которые не подтвердили его теоретические ожидания. [28] - ^ Для математической последовательности Лоренц предложил новую переменную времени, «местное время», названную так, потому что она зависела от положения движущегося тела, следуя соотношению t ′ = t − vx / c 2 . [стр. 13] Лоренц считал местное время не «реальным»; скорее, это представляло собой специальное изменение переменной. [29] : 51, 80
Впечатленный «самой гениальной идеей Лоренца», Пуанкаре увидел в местном времени нечто большее, чем просто математический трюк. Оно представляло собой фактическое время, которое будет показано на часах движущегося наблюдателя. [30] - ^ Эта концепция нелогична хотя бы потому, что, в отличие от обычных понятий расстояния , она может принимать отрицательные значения (не является положительно определенной для несовпадающих событий), а также то, что квадратное обозначение вводит в заблуждение. Этот отрицательный квадрат привел к концепции мнимого времени , которая сейчас широко не используется . Сразу видно, что отрицательное значение Δ s 2 также является инвариантом, порожденным вариантом метрической подписи пространства-времени.
- ^ Инвариантность Δ s 2 при стандартном преобразовании Лоренца аналогично инвариантности квадратов расстояний Δ r 2 при вращениях в евклидовом пространстве. Хотя пространство и время имеют равные права в теории относительности, знак минус перед пространственными терминами отмечает, что пространство и время имеют существенно разный характер. Они не одинаковы. Поскольку оно трактует время иначе, чем три пространственных измерения, пространство Минковского отличается от четырехмерного евклидова пространства .
- ^ Зависимость показателя преломления предполагаемого частичного сопротивления эфира была в конечном итоге подтверждена Питером Зееманом в 1914–1915 годах, спустя много времени после того, как специальная теория относительности была принята общепринятым направлением. Используя увеличенную версию аппарата Майкельсона, подключенную непосредственно к главному водопроводу Амстердама , Зееман смог выполнить расширенные измерения, используя монохроматический свет от фиолетового (4358 Å) до красного (6870 Å). [стр. 17] [стр. 18]
- ↑ Несмотря на то, что прошло много десятилетий с тех пор, как Террелл и Пенроуз опубликовали свои наблюдения, популярные статьи продолжают смешивать размеры и внешний вид. Например, Мичио Каку писал в «Космосе Эйнштейна» (WW Norton & Company, 2004, стр. 65): «...представьте себе, что скорость света составляет всего 20 миль в час. Если бы по улице ехала машина, она может выглядеть сжатым в направлении движения, будучи сжатым, как аккордеон, примерно до 1 дюйма в длину».
- ^ В письме Карлу Зеилигу в 1955 году Эйнштейн написал: «Ранее я уже обнаружил, что теория Максвелла не учитывает микроструктуру излучения и, следовательно, не может иметь общей достоверности», письмо Эйнштейна Карлу Зеилигу, 1955.
- ^ Быстрота возникает естественным образом как координаты чистых буст-генераторов внутри алгебры алгебры Ли группы Лоренца. Точно так же углы поворота естественным образом возникают как координаты (по модулю 2 π ) на генераторах чистого вращения в алгебре Ли. (Вместе они координируют всю алгебру Ли.) Заметное отличие состоит в том, что результирующие вращения являются периодическими по углу поворота, в то время как результирующие повышения не являются периодическими по быстроте (а скорее взаимно однозначными). Сходство между повышениями и ротациями является формальным сходством.
- ^ В теории относительности собственное ускорение — это физическое ускорение (т. е. измеримое ускорение, измеряемое акселерометром), испытываемое объектом. Таким образом, это ускорение относительно свободно падающего или инерционного наблюдателя, который на мгновение находится в состоянии покоя относительно измеряемого объекта.
Первоисточники
[ редактировать ]- ^ Jump up to: а б с д и ж г Альберт Эйнштейн (1905) « Zur Elektrodynamik bewegter Körper », Annalen der Physik 17: 891; Английский перевод Уилфрида Перретта «Об электродинамике движущихся тел» и Джорджа Баркера Джеффри (1923); Еще один английский перевод Об электродинамике движущихся тел» « Мег Над Саха (1920).
- ^ «Наука и здравый смысл», П.В. Бриджмен, The Scientific Monthly , Vol. 79, № 1 (июль 1954 г.), стр. 32–39.
- ^ Электромагнитная масса и импульс вращающегося электрона, Г. Брейт, Труды Национальной академии наук, Том. 12, с.451, 1926 г.
- ^ Кинематика электрона с осью. Фил. Маг. 3:1-22. Л. Х. Томас.]
- ^ Jump up to: а б Эйнштейн, Автобиографические заметки, 1949.
- ^ Эйнштейн, «Фундаментальные идеи и методы теории относительности», 1920 г.
- ^ Эйнштейн, О принципе относительности и выводах, сделанных на его основе, 1907; «Принцип относительности и его последствия в современной физике», 1910; «Теория относительности», 1911 г.; Рукопись по специальной теории относительности, 1912 г.; Теория относительности, 1913; Эйнштейн, «Относительность, специальная и общая теория», 1916; Основные идеи теории относительности, 1916 г.; Что такое теория относительности?, 1919; Принцип относительности (Принстонские лекции), 1921 г.; «Физика и реальность», 1936; Теория относительности, 1949.
- ^ Яаков Фридман (2004). Физическое применение однородных шариков . Прогресс математической физики. Том. 40. стр. 1–21. ISBN 978-0-8176-3339-4 .
- ^ Дас, А. (1993) Специальная теория относительности, математическое изложение , Springer, ISBN 0-387-94042-1 .
- ^ Шутц, Дж. (1997) Независимые аксиомы пространства-времени Минковского, Addison Wesley Longman Limited, ISBN 0-582-31760-6 .
- ^ Лоренц, Х.А. (1902). «Вращение плоскости поляризации в движущихся средах» (PDF) . Институт Гюйгенса — Королевская Нидерландская академия искусств и наук (KNAW) . 4 : 669–678. Бибкод : 1901KNAB....4..669L . Проверено 15 ноября 2018 г.
- ^ Jump up to: а б Лоренц, Х.А. (1904). «Электромагнитные явления в системе, движущейся со скоростью, меньшей скорости света» (PDF) . Институт Гюйгенса — Королевская Нидерландская академия искусств и наук (KNAW) . 6 : 809–831. Бибкод : 1903KNAB....6..809L . Проверено 15 ноября 2018 г.
- ^ Лоренц, Хендрик (1895). «Исследование колебаний, возбуждаемых колеблющимися ионами» . Попытка теории электрических и оптических явлений в движущихся телах . Лейден: Э. Дж. Брилл. (подраздел § 31).
- ^ Линь, Ши-Чунь; Джаллоренци, Томас Г. (1979). «Анализ чувствительности кольцевого оптоволоконного интерферометра на эффекте Саньяка». Прикладная оптика . 18 (6): 915–931. Бибкод : 1979ApOpt..18..915L . дои : 10.1364/AO.18.000915 . ПМИД 20208844 . S2CID 5343180 .
- ^ Шоу, Р. (1962). «Парадокс сокращения длины». Американский журнал физики . 30 (1): 72. Бибкод : 1962AmJPh..30...72S . дои : 10.1119/1.1941907 . S2CID 119855914 .
- ^ Г.А. Бенфорд; DL Book и WA Ньюкомб (1970). «Тахионный антителефон». Физический обзор D . 2 (2): 263–265. Бибкод : 1970PhRvD...2..263B . дои : 10.1103/PhysRevD.2.263 . S2CID 121124132 .
- ^ Зееман, Питер (1914). «Коэффициент Френеля для света разных цветов. (Первая часть)» . Учеб. Кон. акад. Ван Ветен . 17 : 445–451. Бибкод : 1914KNAB...17..445Z .
- ^ Зееман, Питер (1915). «Коэффициент Френеля для света разных цветов. (Вторая часть)» . Учеб. Мог. акад. От знания . 18 : 398–408. Стартовый код : 1915KNAB...18..398Z .
- ^ Террелл, Джеймс (15 ноября 1959 г.). «Невидимость лоренцева сокращения». Физический обзор . 116 (4): 1041–1045. Бибкод : 1959PhRv..116.1041T . дои : 10.1103/PhysRev.116.1041 .
- ^ Пенроуз, Роджер (24 октября 2008 г.). «Видимая форма релятивистски движущейся сферы». Математические труды Кембриджского философского общества . 55 (1): 137–139. Бибкод : 1959PCPS...55..137P . дои : 10.1017/S0305004100033776 . S2CID 123023118 .
- ^ Jump up to: а б с Зависит ли инерция тела от его энергетического содержания? А. Эйнштейн, Annalen der Physik . 18 :639, 1905 г. (английский перевод У. Перретта и Дж. Б. Джеффри)
- ^ Об инерции энергии, требуемой принципом относительности , А. Эйнштейн, Annalen der Physik 23 (1907): 371–384.
- ^ Бальо, Жюльен (26 мая 2007 г.). «Ускорение в специальной теории относительности: что означает «равномерно ускоренное движение»?» (PDF) . Физический факультет, ENS Cachan . Проверено 22 января 2016 г.
- ^ Jump up to: а б с Чемпион, Фрэнк Клайв (1932). «О некоторых близких столкновениях быстрых β-частиц с электронами, сфотографированных методом разложения» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 136 (830). Издательство Королевского общества: 630–637. Бибкод : 1932RSPSA.136..630C . дои : 10.1098/rspa.1932.0108 . S2CID 123018629 .
- ^ Jump up to: а б ПАМ Дирак (1930). «Теория электронов и протонов» . Труды Королевского общества . А126 (801): 360–365. Бибкод : 1930RSPSA.126..360D . дои : 10.1098/rspa.1930.0013 . JSTOR 95359 .
- ^ CD Андерсон (1933). «Положительный электрон» . Физ. Преподобный . 43 (6): 491–494. Бибкод : 1933PhRv...43..491A . дои : 10.1103/PhysRev.43.491 .
Ссылки
[ редактировать ]- ^ Jump up to: а б с Гриффитс, Дэвид Дж. (2013). «Электродинамика и относительность». Введение в электродинамику (4-е изд.). Пирсон. Глава 12. ISBN 978-0-321-85656-2 .
- ^ Jump up to: а б с Джексон, Джон Д. (1999). «Специальная теория относительности». Классическая электродинамика (3-е изд.). John Wiley & Sons, Inc. Глава 11. ISBN 0-471-30932-Х .
- ^ Гольдштейн, Герберт (1980). «Глава 7: Специальная теория относительности в классической механике». Классическая механика (2-е изд.). Издательство Аддисон-Уэсли. ISBN 0-201-02918-9 .
- ^ Jump up to: а б Ланцос, Корнелиус (1970). «Глава IX: Релятивистская механика». Вариационные принципы механики (4-е изд.). Дуврские публикации. ISBN 978-0-486-65067-8 .
- ^ Том Робертс и Зигмар Шляйф (октябрь 2007 г.). «Какова экспериментальная основа специальной теории относительности?» . Usenet Часто задаваемые вопросы по физике . Проверено 17 сентября 2008 г.
- ^ Альберт Эйнштейн (2001). Относительность: специальная и общая теория (перепечатка перевода 1920 года под ред. Роберта В. Лоусона). Рутледж. п. 48. ИСБН 978-0-415-25384-0 .
- ^ Лекции Фейнмана по физике Том. Я Ч. 15-9: Эквивалентность массы и энергии
- ^ Шон Кэрролл, Конспект лекций по общей теории относительности, гл. 1, «Специальная теория относительности и плоское пространство-время», http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html.
- ^ Кокс, Дон (2006). Исследования в области математической физики: концепции элегантного языка (иллюстрированное издание). Springer Science & Business Media. п. 234. ИСБН 978-0-387-32793-8 . Выдержка со страницы 234
- ^ Стейн, Эндрю М. (2012). Относительность стала относительно простой (иллюстрированное издание). ОУП Оксфорд. п. 226. ИСБН 978-0-19-966286-9 . Выдержка со страницы 226
- ^ Эдвин Ф. Тейлор и Джон Арчибальд Уилер (1992). Физика пространства-времени: Введение в специальную теорию относительности . У. Х. Фриман. ISBN 978-0-7167-2327-1 .
- ^ Jump up to: а б с д и Риндлер, Вольфганг (1977). Существенная теория относительности: специальная, общая и космологическая (иллюстрированное изд.). Springer Science & Business Media. п. §1,11 с. 7. ISBN 978-3-540-07970-5 .
- ^ «Джеймс Клерк Максвелл: сила физики» . Мир физики . 01.12.2006 . Проверено 22 марта 2024 г.
- ^ «Ноябрь 1887 года: Майкельсон и Морли сообщают о своей неудаче в обнаружении светоносного эфира» . www.aps.org . Проверено 22 марта 2024 г.
- ^ Майкл Поланьи (1974) Личное знание: на пути к посткритической философии , ISBN 0-226-67288-3 , сноска, стр. 10–11: Эйнштейн сообщает через доктора Н. Бальзаса в ответ на вопрос Поланьи, что «эксперимент Майкельсона-Морли не сыграл никакой роли в основании теории». и «... теория относительности вообще не была создана для объяснения ее результатов». [1]
- ^ Jump up to: а б Йерун ван Донген (2009). «О роли эксперимента Майкельсона-Морли: Эйнштейн в Чикаго». Архив истории точных наук . 63 (6): 655–663. arXiv : 0908.1545 . Бибкод : 2009arXiv0908.1545V . дои : 10.1007/s00407-009-0050-5 . S2CID 119220040 .
- ^ Обзор таких выводов см. Лукас и Ходжсон, Пространство-время и электромагнетизм, 1990.
- ^ Эйнштейн А., Лоренц Х.А., Минковский Х. и Вейль Х. (1952). Принцип относительности: сборник оригинальных мемуаров по специальной и общей теории относительности . Публикации Courier Dover. п. 111. ИСБН 978-0-486-60081-9 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Кольер, Питер (2017). Самая непостижимая вещь: заметки к очень мягкому введению в математику относительности (3-е изд.). Непонятные книги. ISBN 9780957389465 .
- ^ Стейли, Ричард (2009), «Альберт Майкельсон, скорость света и эфирный дрейф», поколение Эйнштейна. Истоки революции относительности , Чикаго: University of Chicago Press, ISBN 0-226-77057-5
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п Дэвид Морин (2007) Введение в классическую механику , Издательство Кембриджского университета, Кембридж, глава 11, Приложение I, ISBN 1-139-46837-5 .
- ^ Миллер, диджей (2010). «Конструктивный подход к специальной теории относительности». Американский журнал физики . 78 (6): 633–638. arXiv : 0907.0902 . Бибкод : 2010AmJPh..78..633M . дои : 10.1119/1.3298908 . S2CID 20444859 .
- ^ Тейлор, Эдвин; Уиллер, Джон Арчибальд (1992). Физика пространства-времени (2-е изд.). WH Freeman & Co. ISBN 978-0-7167-2327-1 .
- ^ Каллахан, Джеймс Дж. (2011). Геометрия пространства-времени: введение в специальную и общую теорию относительности . Нью-Йорк: Спрингер. ISBN 9781441931429 .
- ^ П.Г. Бергманн (1976) Введение в теорию относительности , Дуврское издание, глава IV, стр. 36 ISBN 0-486-63282-2 .
- ^ Мермин, Н. Дэвид (1968). Пространство и время в специальной теории относительности . МакГроу-Хилл. ISBN 978-0881334203 .
- ^ Роберт Резник (1968). Введение в специальную теорию относительности . Уайли. стр. 62–63. ISBN 9780471717249 .
- ^ Jump up to: а б Миллер, Артур И. (1998). Специальная теория относительности Альберта Эйнштейна: возникновение (1905 г.) и ранняя интерпретация (1905–1911 гг.) . Мью-Йорк: Springer-Verlag. ISBN 978-0-387-94870-6 .
- ^ Бернштейн, Джереми (2006). Тайны Старика: Эйнштейн, 1905 год . Книги Коперника (отпечаток Springer Science + Business Media). ISBN 978-0387-26005-1 .
- ^ Дарригол, Оливье (2005). «Происхождение теории относительности» (PDF) . Семинар Пуанкаре . 1 :1–22. Бибкод : 2006eins.book....1D . Проверено 15 ноября 2018 г.
- ^ Jump up to: а б с Риндлер, Вольфганг (1977). Существенная теория относительности (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-10090-6 .
- ^ Jump up to: а б с д Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (1966). Физика пространства-времени (1-е изд.). Сан-Франциско: WH Freeman and Company.
- ^ Эшби, Нил (2003). «Относительность в системе глобального позиционирования» . Живые обзоры в теории относительности . 6 (1): 1. Бибкод : 2003LRR.....6....1A . дои : 10.12942/lrr-2003-1 . ПМЦ 5253894 . ПМИД 28163638 .
- ^ Дэниел Клеппнер и Дэвид Коленкоу (1973). Введение в механику . МакГроу-Хилл. стр. 468–70 . ISBN 978-0-07-035048-9 .
- ^ Jump up to: а б с Французский, AP (1968). Специальная теория относительности . Нью-Йорк: WW Norton & Company. ISBN 0-393-09793-5 .
- ^ Льюис, Гилберт Ньютон; Толман, Ричард Чейз (1909). «Принцип относительности и неньютоновская механика» . Труды Американской академии искусств и наук . 44 (25): 709–726. дои : 10.2307/20022495 . JSTOR 20022495 . Проверено 22 августа 2023 г.
- ^ Jump up to: а б Кувай, Камилло (1971). «Поль Ланжейн и теория относительности» (PDF) . Японские исследования в истории науки . 10 : 113–142 . Проверено 12 июня 2023 г.
- ^ Кэссиди, Дэвид С.; Холтон, Джеральд Джеймс; Резерфорд, Флойд Джеймс (2002). Понимание физики . Спрингер-Верлаг . п. 422. ИСБН 978-0-387-98756-9 .
- ^ Катнер, Марк Лесли (2003). Астрономия, физическая перспектива . Издательство Кембриджского университета . п. 128. ИСБН 978-0-521-82196-4 .
- ^ Эллис, Джордж Ф.Р.; Уильямс, Рут М. (2000). Плоское и искривленное пространство-время (2-е изд.). Издательство Оксфордского университета . стр. 28–29. ISBN 978-0-19-850657-7 .
- ^ Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (2011). Фейнман читает лекции по физике; том I: Издание нового тысячелетия . Основные книги. п. 15-5. ISBN 978-0-465-02414-8 . Проверено 12 июня 2023 г.
- ^ Jump up to: а б Холлидей, Дэвид; Резник, Роберт (1988). Фундаментальная физика: Расширенное третье издание . Нью-Йорк: Джон Уайли и сыновья. стр. 958–959. ISBN 0-471-81995-6 .
- ^ Адамс, Стив (1997). Относительность: введение в физику пространства-времени . ЦРК Пресс . п. 54. ИСБН 978-0-7484-0621-0 .
- ^ Ланжевен, Поль (1911). «Эволюция пространства и времени» . Сциентия . 10 :31–54 . Проверено 20 июня 2023 г.
- ^ Дебс, Талал А.; Рыжий, Майкл Л.Г. (1996). «Парадокс близнецов» и условность одновременности». Американский журнал физики . 64 (4): 384–392. Бибкод : 1996AmJPh..64..384D . дои : 10.1119/1.18252 .
- ^ Толман, Ричард К. (1917). Теория относительности движения . Беркли: Издательство Калифорнийского университета. п. 54.
- ^ Такеучи, Тацу. «Конспекты лекций по специальной теории относительности - Раздел 10» . Вирджинский технологический институт . Проверено 31 октября 2018 г.
- ^ Морен, Дэвид (2017). Специальная теория относительности для начинающих энтузиастов . Независимая издательская платформа CreateSpace. стр. 90–92. ISBN 9781542323512 .
- ^ Гиббс, Филип. «Возможны ли путешествия или связь со скоростью, превышающей скорость света?» . Часто задаваемые вопросы по физике . Департамент математики Калифорнийского университета в Риверсайде . Проверено 31 октября 2018 г.
- ^ Гинзбург, Дэвид (1989). Приложения электродинамики в теоретической физике и астрофизике (иллюстрированное изд.). ЦРК Пресс. п. 206. Бибкод : 1989aetp.book.....G . ISBN 978-2-88124-719-4 . Выдержка со страницы 206
- ^ Уэсли К. Салмон (2006). Четыре десятилетия научных объяснений . Университет Питтсбурга. п. 107. ИСБН 978-0-8229-5926-7 . , раздел 3.7 стр. 107
- ^ Логини, П. (2004). «Измерение скорости света: зачем? Скорость чего?» (PDF) . Материалы Пятой Международной конференции по истории науки в естественнонаучном образовании . Архивировано из оригинала (PDF) 4 июля 2015 года . Проверено 3 июля 2015 г.
- ^ Стэчел, Дж. (2005). «Коэффициент Френеля (перетаскивания) как вызов оптике движущихся тел XIX века» . В Коксе, Эй Джей; Эйзенштадт, Дж (ред.). Вселенная общей теории относительности . Бостон: Биркхойзер. стр. 1–13. ISBN 978-0-8176-4380-5 . Проверено 17 апреля 2012 г.
- ^ Ричард А. Молд (2001). Основная теория относительности (2-е изд.). Спрингер. п. 8. ISBN 978-0-387-95210-9 .
- ^ Зайдельманн, П. Кеннет, изд. (1992). Пояснительное приложение к Астрономическому альманаху . Ил-Вэлли, Калифорния: Университетские научные книги. п. 393. ИСБН 978-0-935702-68-2 .
- ^ Ферраро, Рафаэль; Сфорца, Дэниел М. (2005). «Логотип Европейского физического общества Араго (1810 г.): первый результат эксперимента с эфиром». Европейский журнал физики . 26 (1): 195–204. arXiv : физика/0412055 . Бибкод : 2005EJPh...26..195F . дои : 10.1088/0143-0807/26/1/020 . S2CID 119528074 .
- ^ Долан, Грэм. «Водный телескоп Эйри (1870 г.)» . Королевская обсерватория Гринвич . Проверено 20 ноября 2018 г.
- ^ Холлис, HP (1937). «Водный телескоп Эйри» . Обсерватория . 60 : 103–107. Бибкод : 1937Obs....60..103H . Проверено 20 ноября 2018 г.
- ^ Янссен, Мишель; Стэйчел, Джон (2004). «Оптика и электродинамика движущихся тел» (PDF) . В Стэчеле, Джон (ред.). Становимся критическими . Спрингер. ISBN 978-1-4020-1308-9 .
- ^ Шер, Д. (1968). «Релятивистский эффект Доплера» . Журнал Королевского астрономического общества Канады . 62 : 105–111. Бибкод : 1968JRASC..62..105S . Проверено 11 октября 2018 г.
- ^ Гилл, Т.П. (1965). Эффект Доплера . Лондон: Logos Press Limited. стр. 6–9. ОЛ 5947329М .
- ^ Фейнман, Ричард П .; Лейтон, Роберт Б .; Сэндс, Мэтью (февраль 1977 г.). «Релятивистские эффекты в радиации» . Фейнмановские лекции по физике: Том 1 . Ридинг, Массачусетс: Аддисон-Уэсли . стр. 34–7 ф. ISBN 9780201021165 . LCCN 2010938208 .
- ^ Кук, Хелен. «Релятивистское искажение» . Математический факультет Университета Британской Колумбии . Проверено 12 апреля 2017 г.
- ^ Сигнелл, Питер. «Появления на релятивистских скоростях» (PDF) . Проект ФИЗНЕТ . Университет штата Мичиган, Ист-Лансинг, Мичиган. Архивировано из оригинала (PDF) 13 апреля 2017 года . Проверено 12 апреля 2017 г.
- ^ Краус, Уте. «Мяч круглый» . Путешествие в пространстве и времени: визуализация теории относительности . Институт физики университета Хильдесхайма. Архивировано из оригинала 12 мая 2017 года . Проверено 16 апреля 2017 г.
- ^ Боас, Мэри Л. (1961). «Видимая форма крупных объектов на релятивистских скоростях». Американский журнал физики . 29 (5): 283. Бибкод : 1961AmJPh..29..283B . дои : 10.1119/1.1937751 .
- ^ Мюллер, Томас; Боблест, Себастьян (2014). «Визуальный вид каркасных объектов в специальной теории относительности». Европейский журнал физики . 35 (6): 065025. arXiv : 1410.4583 . Бибкод : 2014EJPh...35f5025M . дои : 10.1088/0143-0807/35/6/065025 . S2CID 118498333 .
- ^ Зенсус, Дж. Антон; Пирсон, Тимоти Дж. (1987). Сверхсветовые радиоисточники (1-е изд.). Кембридж, Нью-Йорк: Издательство Кембриджского университета. п. 3. ISBN 9780521345606 .
- ^ Чейз, Скотт И. «Кажущаяся сверхсветовая скорость галактик» . Оригинальный FAQ по физике Usenet . Департамент математики Калифорнийского университета в Риверсайде . Проверено 12 апреля 2017 г.
- ^ Ричмонд, Майкл. « Сверхсветовые» движения в астрономических источниках» . Физика 200 Конспект лекций . Школа физики и астрономии Рочестерского технологического института. Архивировано из оригинала 16 февраля 2017 года . Проверено 20 апреля 2017 г.
- ^ Кил, Билл. «Джетсы, сверхсветовое движение и гамма-всплески» . Галактики и Вселенная — Конспекты курса WWW . Кафедра физики и астрономии Университета Алабамы. Архивировано из оригинала 1 марта 2017 года . Проверено 29 апреля 2017 г.
- ^ Макс Джаммер (1997). Понятия массы в классической и современной физике . Публикации Courier Dover. стр. 177–178. ISBN 978-0-486-29998-3 .
- ^ Джон Дж. Стэчел (2002). Эйнштейн Б до Я. от Спрингер. п. 221. ИСБН 978-0-8176-4143-6 .
- ^ Фернфлорес, Франциско (2018). Уравнение массы-энергии Эйнштейна, том I: Ранняя история и философские основы . Нью-Йорк: Momentum Pres. ISBN 978-1-60650-857-2 .
- ^ Jump up to: а б Филип Гиббс и Дон Кокс. «Релятивистская ракета» . Проверено 30 августа 2012 г.
- ^ Специальная теория относительности показывает, что на время и пространство влияет движение. Архивировано 21 октября 2012 г. в Wayback Machine . Library.thinkquest.org. Проверено 24 апреля 2013 г.
- ^ Jump up to: а б Идема, Тимон (17 апреля 2019 г.). «Механика и относительность. Глава 14: Релятивистские столкновения» . LibreTexts Физика . Программа доступных решений для обучения Калифорнийского государственного университета . Проверено 2 января 2023 г.
- ^ Накель, Вернер (1994). «Элементарный процесс тормозного излучения». Отчеты по физике . 243 (6): 317–353. Бибкод : 1994PhR...243..317N . дои : 10.1016/0370-1573(94)00068-9 .
- ^ Халберт, ML (1972). «Обзор экспериментов по тормозному излучению нуклон-нуклон». В Остине, С.М.; Кроули, генеральный директор (ред.). Двухчастичная сила в ядрах . Бостон, Массачусетс: Спрингер.
- ^ Jump up to: а б с Ошибка цитирования: именованная ссылка
Taylorбыл вызван, но так и не был определен (см. страницу справки ). - ^ Томас, Джордж Б.; Вейр, Морис Д.; Хасс, Джоэл; Джордано, Фрэнк Р. (2008). Исчисление Томаса: ранние трансценденталии (одиннадцатое изд.). Бостон: Pearson Education, Inc., с. 533. ИСБН 978-0-321-49575-4 .
- ^ Тейлор, Эдвин Ф.; Уиллер, Джон Арчибальд (1992). Физика пространства-времени (2-е изд.). У. Х. Фриман. ISBN 0-7167-2327-1 .
- ^ Jump up to: а б Э.Дж. Пост (1962). Формальная структура электромагнетизма: общая ковариация и электромагнетизм . Dover Publications Inc. ISBN 978-0-486-65427-0 .
- ^ Jump up to: а б с Шютц, Бернард Ф. (1985). Первый курс общей теории относительности . Кембридж, Великобритания: Издательство Кембриджского университета. п. 26. ISBN 0521277035 .
- ^ Jump up to: а б Гиббс, Филип. «Может ли специальная теория относительности справиться с ускорением?» . Часто задаваемые вопросы по физике и теории относительности . math.ucr.edu. Архивировано из оригинала 7 июня 2017 года . Проверено 28 мая 2017 г.
- ^ Франклин, Джерролд (2010). «Лоренцево сокращение, космические корабли Белла и движение твердого тела в специальной теории относительности». Европейский журнал физики . 31 (2): 291–298. arXiv : 0906.1919 . Бибкод : 2010EJPh...31..291F . дои : 10.1088/0143-0807/31/2/006 . S2CID 18059490 .
- ^ Jump up to: а б с Ошибка цитирования: именованная ссылка
Baisбыл вызван, но так и не был определен (см. страницу справки ). - ^ Р. Резник; Р. Айсберг (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Джон Уайли и сыновья. стр. 114–116 . ISBN 978-0-471-87373-0 .
- ^ Ойвинд Грён и Сигбьёрн Хервик (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии . Спрингер. стр. 195. ISBN 978-0-387-69199-2 . Отрывок со страницы 195 (с единицами измерения, где c = 1)
- ^ Количество работ огромно, см. пример:
Сидни Коулман; Шелдон Л. Глэшоу (1997). «Космические лучи и нейтринные тесты специальной теории относительности». Буквы по физике Б. 405 (3–4): 249–252. arXiv : hep-ph/9703240 . Бибкод : 1997PhLB..405..249C . дои : 10.1016/S0370-2693(97)00638-2 . S2CID 17286330 .
Обзор можно найти на этой странице - ^ Робертс, Том; Шлейф, Зигмар. «Эксперименты, которые явно НЕ согласуются с SR/GR» . Какова экспериментальная основа специальной теории относительности? . Калифорнийский университет в Риверсайде . Проверено 10 июля 2024 г.
- ^ Джон Д. Нортон, Джон Д. (2004). «Исследования Эйнштейном галилеевой ковариантной электродинамики до 1905 года» . Архив истории точных наук . 59 (1): 45–105. Бибкод : 2004AHES...59...45N . дои : 10.1007/s00407-004-0085-6 . S2CID 17459755 .
- ^ Дж. А. Уилер; К. Миснер; К. С. Торн (1973). Гравитация . WH Freeman & Co. с. 58. ИСБН 978-0-7167-0344-0 .
- ^ Дж. Р. Форшоу; А.Г. Смит (2009). Динамика и относительность . Уайли. п. 247. ИСБН 978-0-470-01460-8 .
- ^ Р. Пенроуз (2007). Дорога к реальности . Винтажные книги. ISBN 978-0-679-77631-4 .
- ^ Жан-Бернар Зубер и Клод Ицыксон, Квантовая теория поля , стр. 5, ISBN 0-07-032071-3
- ^ Чарльз В. Миснер , Кип С. Торн и Джон А. Уилер , Гравитация , стр. 51, ISBN 0-7167-0344-0
- ^ Джордж Стерман , Введение в квантовую теорию поля , стр. 4, ISBN 0-521-31132-2
- ^ Шон М. Кэрролл (2004). Пространство-время и геометрия: введение в общую теорию относительности . Эддисон Уэсли. п. 22. ISBN 978-0-8053-8732-2 .
Дальнейшее чтение
[ редактировать ]Тексты Эйнштейна и тексты по истории специальной теории относительности
[ редактировать ]- Эйнштейн, Альберт (1920). Теория относительности: специальная и общая теория .
- Эйнштейн, Альберт (1996). Смысл относительности . Тонкие коммуникации. ISBN 1-56731-136-9
- Логунов, Анатолий А. (2005). Анри Пуанкаре и теория относительности (пер. с русского Г. Понтокорво и В. О. Соловьева под редакцией В. А. Петрова). Наука, Москва.
Учебники
[ редактировать ]- Чарльз Миснер , Кип Торн и Джон Арчибальд Уилер (1971) Гравитация . WH Фриман и Ко. ISBN 0-7167-0334-3
- Пост, EJ, 1997 (1962) Формальная структура электромагнетизма: общая ковариация и электромагнетизм . Дуврские публикации.
- Вольфганг Риндлер (1991). Введение в специальную теорию относительности (2-е изд.), Oxford University Press. ISBN 978-0-19-853952-0 ; ISBN 0-19-853952-5
- Харви Р. Браун (2005). Физическая относительность: структура пространства-времени с динамической точки зрения, Oxford University Press, ISBN 0-19-927583-1 ; ISBN 978-0-19-927583-0
- Кадир, Асгар (1989). Теория относительности: введение в специальную теорию . Сингапур: Мировые научные публикации . п. 128. Бибкод : 1989rist.book.....Q . ISBN 978-9971-5-0612-4 .
- Французский, AP (1968). Специальная теория относительности (Вводная физика Массачусетского технологического института) (1-е изд.). WW Нортон и компания. ISBN 978-0393097931 .
- Зильберштейн, Людвик (1914). Теория относительности .
- Лоуренс Склар (1977). Пространство, время и пространство-время . Издательство Калифорнийского университета. ISBN 978-0-520-03174-6 .
- Лоуренс Склар (1992). Философия физики . Вествью Пресс. ISBN 978-0-8133-0625-4 .
- Sergey Stepanov (2018). Relativistic World . De Gruyter. ISBN 9783110515879 .
- Тейлор, Эдвин и Джон Арчибальд Уиллер (1992). Физика пространства-времени (2-е изд.). WH Фриман и Ко. ISBN 0-7167-2327-1 .
- Типлер, Пол, и Ллевеллин, Ральф (2002). Современная физика (4-е изд.). WH Фриман и Ко. ISBN 0-7167-4345-0 .
Журнальные статьи
[ редактировать ]- Альвагер, Т.; Фарли, FJM; Кьельман, Дж.; Валлин, Л.; и др. (1964). «Проверка второго постулата специальной теории относительности в области ГэВ». Письма по физике . 12 (3): 260–262. Бибкод : 1964PhL....12..260A . дои : 10.1016/0031-9163(64)91095-9 .
- Дарригол, Оливье (2004). «Тайна связи Пуанкаре-Эйнштейна». Исида . 95 (4): 614–26. дои : 10.1086/430652 . ПМИД 16011297 . S2CID 26997100 .
- Вольф, Питер; Пети, Жерар (1997). «Спутниковое испытание специальной теории относительности с использованием системы глобального позиционирования». Физический обзор А. 56 (6): 4405–09. Бибкод : 1997PhRvA..56.4405W . дои : 10.1103/PhysRevA.56.4405 .
- Специальная стипендия теории относительности
- Риндлер, Вольфганг (2011). «Специальная теория относительности: Кинематика» . Схоларпедия . 6 (2): 8520. Бибкод : 2011SchpJ...6.8520R . doi : 10.4249/scholarpedia.8520 .
Внешние ссылки
[ редактировать ]Оригинальные работы
[ редактировать ]- Об электродинамике движущихся тел Оригинальная работа Эйнштейна на немецком языке «Анналы физики» , Берн , 1905 г.
- Английский перевод «К электродинамике движущихся тел» , опубликованный в книге « Принцип относительности» 1923 года .
Специальная теория относительности для широкой аудитории (математические знания не требуются)
[ редактировать ]- Einstein Light . Отмеченное наградами нетехническое введение (видеоклипы и демонстрации), подкрепленное десятками страниц дальнейших объяснений и анимаций на уровнях с математикой или без нее
- Эйнштейн, онлайн- архив. Архивировано 1 февраля 2010 г. в Wayback Machine. Введение в теорию относительности, Институт гравитационной физики Макса Планка.
- Аудио: Каин/Гей (2006) – Астрономический состав . Специальная теория относительности Эйнштейна
Объяснение специальной теории относительности (с использованием простой или более сложной математики)
[ редактировать ]- Bondi K-Calculus – Простое введение в специальную теорию относительности.
- Грега Игана. Фонды Архивировано 25 апреля 2013 г. в Wayback Machine .
- Заметки Хогга по специальной теории относительности. Хорошее введение в специальную теорию относительности на уровне бакалавриата с использованием математического анализа.
- Калькулятор относительности: Специальная теория относительности. Архивировано 21 марта 2013 г. на Wayback Machine . Вывод алгебраического и интегрального исчисления для E = mc. 2 .
- MathPages – Размышления об относительности Полная онлайн-книга по теории относительности с обширной библиографией.
- Специальная теория относительности. Введение в специальную теорию относительности на уровне бакалавриата.
- Относительность: специальная и общая теория в проекте «Гутенберг» , Альберт Эйнштейн
- Конспекты лекций по специальной теории относительности — это стандартное введение в специальную теорию относительности, содержащее иллюстративные пояснения, основанные на рисунках и диаграммах пространства-времени, полученных в Политехническом институте Вирджинии и Государственном университете.
- Понимание специальной теории относительности. Специальная теория относительности в доступной для понимания форме.
- «Введение в специальную теорию относительности» (1964) Роберта Каца, «введение… которое доступно любому студенту, знакомому с общей физикой и имеющему некоторое представление о математическом анализе» (130 стр.; формат pdf) .
- Конспект лекций по специальной теории относительности Дж. Д. Крессера, факультет физики Университета Маккуори.
- SpecialRelativity.net – обзор с визуализацией и минимальной математикой.
- Относительность 4-когда-нибудь? В занимательной форме обсуждается проблема сверхсветового движения.
Визуализация
[ редактировать ]- Программное обеспечение специальной теории относительности для трассировки лучей, визуализирующее несколько сценариев под влиянием специальной теории относительности.
- Относительность в реальном времени. Архивировано 8 мая 2013 г. в Wayback Machine , Австралийский национальный университет. Релятивистские визуальные эффекты, наблюдаемые с помощью интерактивной программы.
- Путешествие в пространстве-времени. Разнообразные визуализации релятивистских эффектов, от релятивистского движения до черных дыр.
- Глазами Эйнштейна. Архивировано 14 мая 2013 г. в Wayback Machine , Австралийский национальный университет. Релятивистские визуальные эффекты, объясненные с помощью фильмов и изображений.
- Специальный симулятор относительности Warp Компьютерная программа, демонстрирующая эффекты путешествий со скоростью, близкой к скорости света.
- Анимационный клип на YouTube, визуализирующий преобразование Лоренца.
- Оригинальные интерактивные FLASH-анимации Джона де Пиллиса, иллюстрирующие системы Лоренца и Галилея, парадокс поезда и туннеля, парадокс близнецов, распространение волн, синхронизацию часов и т. д.
- Lightspeed Программа на основе OpenGL, разработанная для иллюстрации влияния специальной теории относительности на внешний вид движущихся объектов.
- Анимация, показывающая звезды вблизи Земли, как видно с космического корабля, быстро разгоняющегося до скорости света.
















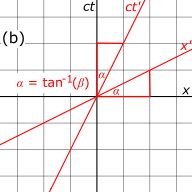

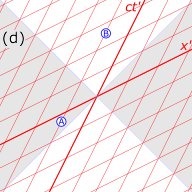









































































































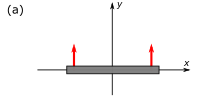


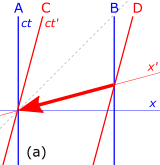












![{\displaystyle \sin \theta '={\frac {\sin \theta }{\gamma [1+(v/c)\cos \theta ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b1d959a5aa9840f249611011e804cba5079e53)


















![{\displaystyle {\begin{aligned}E_{0}&=E_{1}+{\tfrac {1}{2}}L+{\tfrac {1}{2}}L=E_{1}+L\\[5mu]H_{0}&=H_{1}+{\tfrac {1}{2}}L{\frac {1-(v/c)\cos {\phi }}{\sqrt {1-v^{2}/c^{2}}}}+{\tfrac {1}{2}}L{\frac {1+(v/c)\cos {\phi }}{\sqrt {1-v^{2}/c^{2}}}}=H_{1}+{\frac {L}{\sqrt {1-v^{2}/c^{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/343ffb26e1d6fe9149832c6e8b3f2ef79fecad0c)