Аффинное соединение

Аффинная связность на сфере перекатывает аффинную касательную плоскость из одной точки в другую. При этом точка контакта очерчивает кривую на плоскости: развитие .

В дифференциальной геометрии аффинная связность Это геометрический объект на гладком многообразии , который соединяет близлежащие касательные пространства , поэтому он позволяет касательные векторные поля, дифференцировать как если бы они были функциями на многообразии со значениями в фиксированном векторном пространстве . Связности — один из простейших способов задания дифференцирования сечений расслоений векторных .

Понятие аффинной связи уходит корнями в геометрию и тензорное исчисление XIX века , но не было полностью разработано до начала 1920-х годов Эли Картаном (как часть его общей теории связей ) и Германом Вейлем (который использовал это понятие как часть его основ общей теории относительности ). Терминология принадлежит Картану. и берет свое начало в идентификации касательных пространств в евклидовом пространстве R ^н в переводе: идея состоит в том, что выбор аффинной связности делает многообразие бесконечно похожим на евклидово пространство не просто гладко, а как аффинное пространство .

На любом многообразии положительной размерности имеется бесконечное число аффинных связностей. Если многообразие дополнительно наделено метрическим тензором, то существует естественный выбор аффинной связности, называемой связностью Леви-Чивита . Выбор аффинной связности эквивалентен предписанию способа дифференцирования векторных полей, удовлетворяющего нескольким разумным свойствам ( линейности и правилу Лейбница ). Это дает возможное определение аффинной связности как ковариантной производной или (линейной) связности на касательном расслоении . Выбор аффинной связи также эквивалентен понятию параллельного транспорта , который представляет собой метод транспортировки касательных векторов вдоль кривых. Это также определяет параллельную транспортировку пакета кадров . Бесконечно малый параллельный транспорт в пакете кадров дает другое описание аффинного соединения: либо как соединение Картана для аффинной группы , либо как основное соединение в пакете кадров.

Основными инвариантами аффинной связности являются ее кручение и кривизна . Кручение измеряет, насколько точно скобка Ли векторных полей может быть восстановлена ​​из аффинной связности. Аффинные связи также могут использоваться для определения (аффинных) геодезических на многообразии, обобщая прямые линии евклидова пространства, хотя геометрия этих прямых может сильно отличаться от обычной евклидовой геометрии ; основные различия заключены в кривизне соединения.

Мотивация и история

Гладкое многообразие — это математический объект, который локально выглядит как гладкая деформация евклидова пространства R. ^н : например, гладкая кривая или поверхность локально выглядит как плавная деформация линии или плоскости. Гладкие функции и векторные поля можно определить на многообразиях так же, как и в евклидовом пространстве, а скалярные функции на многообразиях можно дифференцировать естественным образом. Однако дифференцирование векторных полей менее прямолинейно: это простой вопрос в евклидовом пространстве, потому что касательное пространство базовых векторов в точке p может быть отождествлено естественным образом (путем перевода) с касательным пространством в соседней точке q . На общем многообразии нет такой естественной идентификации между близлежащими касательными пространствами, и поэтому касательные векторы в соседних точках нельзя сравнивать четко определенным образом. Понятие аффинной связности было введено, чтобы решить эту проблему путем соединения близлежащих касательных пространств. Истоки этой идеи можно проследить до двух основных источников: теории поверхностей и тензорного исчисления .

поверхностной

См. Также: Картановское соединение.

Рассмотрим гладкую поверхность S в трехмерном евклидовом пространстве. Вблизи любой точки S можно аппроксимировать касательной плоскостью в этой точке, которая является аффинным подпространством евклидова пространства. Дифференциальные геометры XIX века интересовались идеей развития , при которой одна поверхность катилась по другой, без скольжения и скручивания . В частности, касательную плоскость к точке S можно катить по S : это легко представить, когда S представляет собой поверхность, подобную 2-сфере, которая является гладкой границей выпуклой области . Когда касательная плоскость катится по S , точка контакта очерчивает кривую S. на есть кривая И наоборот, если на S , касательная плоскость может катиться вдоль этой кривой. Это дает возможность идентифицировать касательные плоскости в разных точках кривой: в частности, касательный вектор в касательном пространстве в одной точке кривой отождествляется с уникальным касательным вектором в любой другой точке кривой. Эти отождествления всегда задаются аффинными преобразованиями. из одной касательной плоскости в другую.

Это представление о параллельном переносе касательных векторов посредством аффинных преобразований вдоль кривой имеет характерную особенность: точка контакта касательной плоскости с поверхностью всегда движется вместе с кривой при параллельном переносе (т. е. когда касательная плоскость катится вдоль поверхность, точка контакта движется). Это родовое состояние характерно для связей Картана . В более современных подходах точка контакта рассматривается как начало координат в касательной плоскости (которая в этом случае является векторным пространством), а движение начала координат корректируется перемещением, так что параллельный перенос является линейным, а не аффинным.

Однако с точки зрения связностей Картана аффинные подпространства евклидова пространства являются модельными поверхностями — они являются простейшими поверхностями в евклидовом 3-пространстве и однородны относительно аффинной группы плоскости — и каждая гладкая поверхность имеет уникальную поверхность модели, касательная к ней в каждой точке. Эти поверхности модели являются геометриями Клейна в смысле Феликса Кляйна программы Эрлангена . В более общем смысле, n -мерное аффинное пространство — это геометрия Клейна для аффинной группы Aff( n ) , стабилизатором точки является общая линейная группа GL( n ) . Тогда аффинное n- многообразие — это многообразие, которое бесконечно похоже на n -мерное аффинное пространство.

Мотивация

Смотрите также: Ковариантная производная

Исторически люди использовали ковариантную производную (или связь Леви-Чивита, определяемую метрикой) для описания скорости изменения вектора вдоль направления другого вектора. Здесь, в проколотом двумерном евклидовом пространстве, синее векторное поле X переводит одноформенную форму d r повсюду в 0,07. Красное векторное поле Y переводит одну форму r d θ в 0,5 r повсюду. Подтверждено метрикой d s ² = д р ² + р ² буду я ² , связность Леви-Чивита ∇ _Y X везде равна 0, что указывает на то, что X не изменяется вдоль Y . Другими словами, X параллельно перемещается по каждой концентрической окружности. ∇ _X Y = Y / r повсюду, что приводит к тому, что r d θ везде становится равным 0,5, подразумевая, что Y имеет «постоянную» скорость изменения в радиальном направлении.

Вторая мотивация аффинных связей исходит из понятия ковариантной производной векторных полей. До появления координатно-независимых методов необходимо было работать с векторными полями, встраивая соответствующие им евклидовы векторы в атлас . Эти компоненты можно дифференцировать, но производные не преобразуются управляемым образом при изменении координат. Поправочные члены были введены Элвином Бруно Кристоффелем (следуя идеям Бернхарда Римана ) в 1870-х годах, так что (скорректированная) производная одного векторного поля вдоль другого трансформировалась ковариантно при преобразованиях координат — эти поправочные члены впоследствии стали известны как символы Кристоффеля .

Эта идея была развита в теорию абсолютного дифференциального исчисления (теперь известного как тензорное исчисление ) Грегорио Риччи-Курбастро и его учеником Туллио Леви-Чивита между 1880 годом и началом 20-го века.

Однако тензорное исчисление действительно ожило с появлением Альберта Эйнштейна общей теории относительности в 1915 году. Через несколько лет после этого Леви-Чивита формализовал уникальную связь, связанную с римановой метрикой, теперь известную как Леви -Чивита. связь . Более общие аффинные связи были затем изучены примерно в 1920 году Германом Вейлем . разработавший детальное математическое обоснование общей теории относительности, и Эли Картан , который установил связь с геометрическими идеями, исходящими из теории поверхностей.

Подходы

Сложная история привела к развитию самых разных подходов и обобщений концепции аффинной связи.

Самым популярным подходом, вероятно, является определение, основанное на ковариантных производных. С одной стороны, идеи Вейля были подхвачены физиками в виде калибровочной теории и калибровочных ковариантных производных . С другой стороны, понятие ковариантной дифференциации было абстрагировано Жаном-Луи Кошулем , который определил (линейные или Кошуля) связи на векторных расслоениях . На этом языке аффинная связность — это просто ковариантная производная или (линейная) связность на касательном расслоении .

Однако этот подход не объясняет ни геометрию аффинных связей, ни то, как они получили свое название. Этот термин действительно имеет свое происхождение от идентификации касательных пространств в евклидовом пространстве путем перевода: это свойство означает, что евклидово n -пространство является аффинным пространством . (Альтернативно евклидово пространство — это главное однородное пространство или торсор группы переводов, которая является подгруппой аффинной группы.) Как упоминалось во введении, есть несколько способов уточнить это: один использует тот факт, что аффинная группа Связь определяет понятие параллельного переноса векторных полей вдоль кривой. Это также определяет параллельную транспортировку пакета кадров . Инфинитезимальный параллельный транспорт в пакете кадров дает другое описание аффинного соединения: либо как соединение Картана для аффинной группы Aff( n ) , либо как основное соединение GL( n ) в пакете кадров.

как дифференциальный

См. также: Ковариантная производная и Соединение (векторное расслоение).

Пусть M гладкое многообразие и Γ(TM ) — пространство векторных полей на M , т. е. пространство гладких сечений касательного расслоения TM — . Тогда аффинная связность на M является билинейным отображением

${\begin{aligned}\Gamma (\mathrm {T} M)\times \Gamma (\mathrm {T} M)&\rightarrow \Gamma (\mathrm {T} M)\\(X,Y)&\mapsto \nabla _{X}Y\,,\end{aligned}}$

такая, что для всех f из множества гладких функций на M , записанных C ^∞ ( M , R ) и все векторные поля X , Y на M :

1. ∇ _fX Y = f ∇ _X Y , то есть ∇ есть C ^∞ ( M , R ) - линейная по первой переменной;
2. ∇ _X ( fY ) = (∂ _X   f ) Y + f ∇ _X Y , где ∂ _X обозначает производную по направлению ; то есть ∇ удовлетворяет правилу Лейбница по второй переменной.

Элементарные свойства

• Из свойства 1 выше следует, что значение ∇ _X Y в точке x ∈ M зависит только от значения X в точке x , а не от значения X в M − { x } . Из свойства 2 выше также следует, что значение ∇ _X Y в точке x ∈ M зависит только от значения Y в окрестности точки x .
• Если ∇ ¹ , ∇ ² то значение ∇ в x точке являются аффинными связями , ¹
  _Икс Y - ∇ ²
  _X Y может быть записано как Γ _x ( X _x , Y _x ) , где
  $$\Gamma _{x}:\mathrm {T} _{x}M\times \mathrm {T} _{x}M\to \mathrm {T} _{x}M$$
  билинейно и гладко зависит от x (т. е. определяет гладкий гомоморфизм расслоения ). Обратно, если ∇ — аффинная связность, а Γ — такой гладкий билинейный гомоморфизм расслоения (называемый формой связности на M ), то ∇ + Γ — аффинная связность.
• Если M — открытое подмножество R ^н , то касательное расслоение к M — это тривиальное расслоение M × R ^н . В этой ситуации существует каноническая аффинная связность d на M : любое векторное поле Y задается гладкой функцией V от M до R. ^н ; тогда d _X Y — векторное поле, соответствующее гладкой функции d V ( X ) = ∂ _X Y от M до R ^н . Поэтому любую другую аффинную связность ∇ на M можно записать ∇ = d + Γ , где — форма связности на M. Γ
• В более общем смысле, локальная тривиализация касательного расслоения — это изоморфизм расслоения между ограничением TM × открытое подмножество U в M и U на R ^н . Тогда ограничение аффинной связности ∇ на U можно записать в виде d + Γ , где Γ — форма связности на U .

Параллельный транспорт для аффинных соединений

См. также: Параллельный транспорт

Параллельный перенос касательного вектора по кривой на сфере.

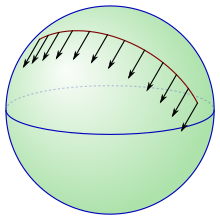
Сравнение касательных векторов в разных точках многообразия обычно не является четко определенным процессом. Аффинное соединение предоставляет один из способов исправить эту ситуацию, используя понятие параллельной транспортировки , и его действительно можно использовать для определения аффинного соединения.

Пусть M — многообразие с аффинной связностью ∇ . Тогда векторное поле X называется параллельным, если ∇ X = 0, в том смысле, что для любого векторного поля ∇ Y Y _X = 0 . Интуитивно говоря, все производные параллельных векторов равны нулю и поэтому в некотором смысле являются постоянными . Оценивая параллельное векторное поле в двух точках x и y идентификацию между касательным вектором в точке x и вектором в точке y , можно получить . Такие касательные векторы называются параллельными переносами друг друга.

Ненулевые параллельные векторные поля, вообще говоря, не существуют, поскольку уравнение ∇ X 0 представляет собой частных производных переопределенное уравнение в : условием интегрируемости этого уравнения является обращение в нуль кривизны ∇ = (см. ниже). Однако если это уравнение ограничить кривой от x до y , оно станет обыкновенным дифференциальным уравнением . Тогда существует единственное решение для любого начального значения X в точке x .

Точнее, если γ : I → M — гладкая кривая , параметризованная интервалом [ a , b ] и ξ ∈ T _x M , где x = γ ( a ) , то векторное поле X вдоль γ (и, в частности, значение этого векторного поля в точке y = γ ( b ) ) называется параллельным переносом ξ вдоль γ , если

1. ∇ _{γ′ ( т )} Икс знак равно 0 , для всех т € [ а , б ]
2. Икс _{γ ( а )} знак равно ξ .

Формально первое условие означает, что X параллельно относительно обратного соединения на расслоении обратного образа γ ∗ TM . Однако в локальной тривиализации это система линейных обыкновенных дифференциальных уравнений первого порядка , которая имеет единственное решение для любого начального условия, заданного вторым условием (например, теоремой Пикара–Линделёфа ).

Таким образом, параллельная транспортировка обеспечивает способ перемещения касательных векторов вдоль кривой с использованием аффинной связи, чтобы они интуитивно оставались «указывающими в одном направлении», и это обеспечивает линейный изоморфизм между касательными пространствами на двух концах кривой. Полученный таким образом изоморфизм, вообще говоря, будет зависеть от выбора кривой: если это не так, то параллельный транспорт вдоль каждой кривой можно использовать для определения параллельных векторных полей на M , что может произойти только в том случае, если кривизна ∇ равна нулю. .

Линейный изоморфизм определяется его действием на упорядоченный базис или фрейм . Следовательно, параллельную транспортировку можно также охарактеризовать как способ транспортировки элементов (касательного) пакета кадров GL( M ) вдоль кривой. Другими словами, аффинная связность обеспечивает подъем любой кривой γ в M до кривой γ̃ в GL( M ) .

Формальное определение комплекта рамок

См. также: Подключение (основной пакет)

Аффинная связность также может быть определена как главная GL( ) ω связность на расслоении реперов F M или GL( M ) многообразия M. n Более подробно, ω — гладкое отображение касательного расслоения T(F M ) расслоения реперов в пространство матриц размера n × n (которое является алгеброй Ли gl ( n ) группы Ли GL( n ) обратимых матрицы размера n × n ), удовлетворяющие двум свойствам:

1. ω эквивариантно n относительно действия GL( ) на T ( FM ) и gl ( n ) ;
2. ω ( X _ξ ) = ξ для любого ξ в gl ( n ) , где X _ξ — векторное поле на F M , соответствующее ξ .

Такая связность ω сразу определяет ковариантную производную не только на касательном расслоении, но и на векторных расслоениях , ассоциированных с любым групповым представлением GL ( n ) , включая расслоения тензоров и тензорных плотностей . И наоборот, аффинная связность на касательном расслоении определяет аффинную связность на расслоении фреймов, например, требуя, чтобы ω обращалась в нуль на касательных векторах к подъемам кривых к расслоению фреймов, определенному параллельным переносом.

В комплект рамы также входит пайка формы θ : T(F M ) → R ^н который горизонтален в том смысле, что он обращается в нуль на вертикальных векторах , таких как точечные значения векторных полей X _ξ : Действительно, θ определяется сначала путем проецирования касательного вектора (к F M в системе отсчета f ) на M , а затем путем взятия компоненты этого касательного вектора на M относительно системы отсчета f . Обратите внимание, что θ также GL( n ) -эквивариантен (где GL( n ) действует на R ^н путем матричного умножения).

Пара ( θ , ω ) определяет изоморфизм расслоения T (F M ) тривиальным расслоением F M × aff ( n ) , где aff ( n ) — декартово произведение R с ^н и gl ( n ) (рассматривается как алгебра Ли аффинной группы, которая на самом деле является полупрямым произведением – см. ниже).

Аффинные соединения

См. Также: Картановское соединение.

Аффинные соединения могут быть определены в рамках общей структуры Картана. В современном подходе это тесно связано с определением аффинных связностей на связке фреймов. Действительно, в одной формулировке связность Картана — это абсолютный параллелизм главного расслоения, удовлетворяющего подходящим свойствам. С этой точки зрения aff ( n ) -значная однозначная форма ( θ , ω ) : T(F M ) → aff ( n ) на расслоении реперов (аффинного многообразия ) является связностью Картана. Однако первоначальный подход Картана отличался от этого во многих отношениях:

• понятия пакетов фреймов или основных пакетов не существовало;
• связь рассматривалась как параллельный транспорт между бесконечно близкими точками;
• этот параллельный транспорт был аффинным, а не линейным;
• перевозимые объекты были не касательными векторами в современном понимании, а элементами аффинного пространства с отмеченной точкой, которую картановская связь в конечном итоге отождествляет с касательным пространством.

Объяснения и историческая интуиция

Только что поднятые вопросы легче всего объяснить наоборот, исходя из мотивации, обеспечиваемой теорией поверхности. В этой ситуации, хотя плоскости, катящиеся по поверхности, в наивном смысле являются касательными плоскостями, понятие касательного пространства на самом деле является бесконечно малым понятием. тогда как плоскости как аффинные подпространства в R ³ , бесконечны по протяженности. Однако все эти аффинные плоскости имеют отмеченную точку, точку контакта с поверхностью, и в этой точке они касаются поверхности. Таким образом, возникает путаница, поскольку аффинное пространство с отмеченной точкой можно отождествить с касательным пространством в этой точке. Однако параллельный перенос, определяемый прокаткой, не фиксирует это происхождение: он скорее аффинный , чем линейный; линейный параллельный транспорт можно восстановить, применив трансляцию.

Абстрагируя эту идею, аффинное многообразие, следовательно, должно быть с аффинным пространством Ax размерности _n n , прикрепленным к каждому x ∈ M в отмеченной точке ax _M ∈ Ax _{-многообразием} вместе с методом транспортировки элементов эти аффинные пространства вдоль любой кривой C в M . Этот метод должен удовлетворять нескольким свойствам:

1. для любых двух точек x , y на C параллельный транспорт — это аффинное преобразование из A _x в A _y ;
2. параллельный транспорт определяется бесконечно малым в том смысле, что он дифференцируем в любой точке C и зависит только от касательного вектора к C в этой точке;
3. производная параллельного переноса в точке x определяет линейный изоморфизм от T _x M до T _{a x} A _x .

Эти последние два пункта довольно сложно уточнить, поэтому аффинные связи чаще определяются бесконечно малыми. Чтобы обосновать это, достаточно рассмотреть, как аффинные системы отсчета трансформируются бесконечно мало по отношению к параллельной транспортировке. (Это источник метода перемещения кадров .) Аффинный кадр в точке состоит из списка ( p , e ₁ ,… en _{Картана} ) , где p ∈ A _x и e _i образуют основу T _p ( A _x ) . Тогда аффинная связность символически задается дифференциальной системой первого порядка.

$(*){\begin{cases}\mathrm {d} {p}&=\theta ^{1}\mathbf {e} _{1}+\cdots +\theta ^{n}\mathbf {e} _{n}\\\mathrm {d} \mathbf {e} _{i}&=\omega _{i}^{1}\mathbf {e} _{1}+\cdots +\omega _{i}^{n}\mathbf {e} _{n}\end{cases}}\quad i=1,2,\ldots ,n$

определяется набором одноформ ( θ ^дж , ой ^дж
_я ) . Геометрически аффинная система отсчета претерпевает перемещение вдоль кривой γ от γ ( t ) до γ ( t + δt ) , заданное (приблизительно или бесконечно мало) формулой

${\begin{aligned}p(\gamma (t+\delta t))-p(\gamma (t))&=\left(\theta ^{1}\left(\gamma '(t)\right)\mathbf {e} _{1}+\cdots +\theta ^{n}\left(\gamma '(t)\right)\mathbf {e} _{n}\right)\mathrm {\delta } t\\\mathbf {e} _{i}(\gamma (t+\delta t))-\mathbf {e} _{i}(\gamma (t))&=\left(\omega _{i}^{1}\left(\gamma '(t)\right)\mathbf {e} _{1}+\cdots +\omega _{i}^{n}\left(\gamma '(t)\right)\mathbf {e} _{n}\right)\delta t\,.\end{aligned}}$

Более того, аффинные пространства A _x должны касаться M в неформальном смысле, что смещение x _точке вдоль γ можно отождествить (приблизительно или бесконечно мало) с вектором касания γ ′( t ) к γ в x = γ ( t ) (что является бесконечно малым смещением x ). С

$a_{x}(\gamma (t+\delta t))-a_{x}(\gamma (t))=\theta \left(\gamma '(t)\right)\delta t\,,$

где θ определяется формулой θ ( X ) = θ ¹ ( Икс ) е ₁ + … + я ^н ( X ) en _θ , это отождествление задается θ , поэтому требование состоит в том, чтобы был линейным изоморфизмом в каждой точке.

касательное аффинное пространство A _x интуитивно отождествляется с бесконечно малой аффинной окрестностью x Таким образом , .

Современная точка зрения уточняет всю эту интуицию с помощью главных расслоений (основная идея состоит в том, чтобы заменить фрейм или переменный фрейм пространством всех фреймов и функций на этом пространстве). Он также черпает вдохновение из Феликса Кляйна в программы Эрлангене . в котором геометрия определяется как однородное пространство . В этом смысле аффинное пространство является геометрией и снабжено плоской связностью Картана. Таким образом, общее аффинное многообразие рассматривается как искривленная деформация геометрии плоской модели аффинного пространства.

Аффинное пространство как геометрия плоской модели

Определение аффинного пространства

Неформально аффинное пространство — это векторное пространство без фиксированного выбора начала координат . Он описывает геометрию точек и свободных векторов в пространстве. Из-за отсутствия начала координат точки в аффинном пространстве не могут быть сложены вместе, поскольку для этого требуется выбор начала координат, с помощью которого можно сформировать закон параллелограмма для сложения векторов. Однако вектор v можно добавить к точке p , поместив начальную точку вектора в точку p и затем перенеся p в конечную точку. Описанная таким образом операция p → p + v представляет сдвиг p собой вдоль v . С технической точки зрения аффинное n -пространство — это множество A ^н снабжено свободным транзитивным действием векторной группы R ^н на нем посредством этой операции перевода точек: А ^н таким образом, является главным однородным пространством для векторной группы R ^н .

Общая линейная группа GL( n ) — это преобразований R группа ^н сохраняющие структуру R линейную ^н в том смысле, что Т ( av + bw ) = aT ( v ) + bT ( w ) . По аналогии, аффинная группа Aff( n ) — это группа преобразований A ^н сохраняя аффинную структуру . Таким образом, φ ∈ Aff( n ) должна сохранять сдвиги в том смысле, что

$\varphi (p+v)=\varphi (p)+T(v)$

где T — общее линейное преобразование. Отображение, переводящее φ ∈ Aff( n ) в T ∈ GL( n ), является групповым гомоморфизмом . Его ядром является группа переводов R ^н . любой Таким образом , стабилизатор точки p в A можно отождествить с GL( n ) с помощью этой проекции: это реализует аффинную группу как полупрямое произведение GL ( n ) и R ^н , а аффинное пространство — как однородное пространство Aff( n )/GL( n ) .

Аффинные фреймы и плоское аффинное соединение

Аффинная шкала для A состоит из точки p ∈ A базиса ( e ₁ ,… en _и ) векторного пространства T _p A = R ^н . Общая линейная группа GL( n ) свободно действует на множестве F A всех аффинных фреймов, фиксируя и преобразуя базис ( e1 _p … en _, ) обычным способом, а отображение π отправляет аффинный фрейм ( p ; e ₁ ,… en _- ) в p — это фактор отображение . Таким образом, A является главным GL ( n ) -расслоением над A. F Действие GL( n ) до свободного транзитивного действия аффинной группы Aff( n ) на F A , так что F A является Aff( n ) -торсором A , а выбор системы отсчета идентифицирует F естественным образом продолжается → A с главным расслоением Aff( n ) → Aff( n )/GL( n ) .

На F A существует набор из n + 1 функций, определяемых формулами

$\pi (p;\mathbf {e} _{1},\dots ,\mathbf {e} _{n})=p$

(как и раньше) и

$\varepsilon _{i}(p;\mathbf {e} _{1},\dots ,\mathbf {e} _{n})=\mathbf {e} _{i}\,.$

После выбора базовой точки для A все это функции со значениями в R. ^н , поэтому можно взять их внешние производные для получения дифференциальных 1-форм со значениями в R ^н . Поскольку функции ε _i дают базис для R ^н в каждой точке F A эти 1-формы должны быть выразимы в виде сумм вида

${\begin{aligned}\mathrm {d} \pi &=\theta ^{1}\varepsilon _{1}+\cdots +\theta ^{n}\varepsilon _{n}\\\mathrm {d} \varepsilon _{i}&=\omega _{i}^{1}\varepsilon _{1}+\cdots +\omega _{i}^{n}\varepsilon _{n}\end{aligned}}$

для некоторого набора ( θ ^я , ой ^к
_j ) _{1 ⩽ i , j , k ⩽ n} вещественных одноформ на Aff( n ) . Эта система одноформ на главном расслоении F A → A определяет аффинную связность на A .

Взяв внешнюю производную второй раз и воспользовавшись тем фактом, что d ² = 0 а также линейной независимости ε , _i получены следующие соотношения:

${\begin{aligned}\mathrm {d} \theta ^{j}-\sum _{i}\omega _{i}^{j}\wedge \theta ^{i}&=0\\\mathrm {d} \omega _{i}^{j}-\sum _{k}\omega _{k}^{j}\wedge \omega _{i}^{k}&=0\,.\end{aligned}}$

Это уравнения Маурера–Картана для группы Ли Aff( n ) (отождествляемой с F A выбором системы отсчета). Более того:

• система Пфаффа θ ^дж = 0 (для всех ) интегрируемо , а его целочисленные многообразия являются слоями главного расслоения Aff( n ) → A. j
• система Пфаффа ω ^дж
  _i = 0 (для всех , j ) также интегрируемо, и его интегральные многообразия определяют параллельный перенос в F A. i

Таким образом, формы ( ω ^дж
_i ) определить плоскую главную на F A → A. связность

Для строгого сравнения с мотивацией фактически следует определить параллельный транспорт в главном ( n ) -расслоении над A. Aff Это можно сделать, назад отведя F A по гладкому отображению φ : R ^н × A → A определяется переводом. Тогда композиция φ ′ ∗ F A → F A → A является главным Aff( n ) -расслоением над A и формы ( θ ^я , ой ^к
_j ) откатиться назад , чтобы получить плоскую главную Aff( n ) -связность на этом расслоении.

аффинные геометрии:

Аффинное пространство, как и любая гладкая геометрия Клейна , представляет собой многообразие, снабженное плоской связностью Картана. Более общие аффинные многообразия или аффинные геометрии легко получить, отбросив условие плоскостности, выраженное уравнениями Маурера-Картана. Существует несколько подходов к этому определению, и будут даны два. Оба определения облегчаются осознанием того, что 1-формы ( θ ^я , ой ^к
_j ) в плоской модели совмещаются, образуя 1-форму со значениями в алгебре Ли aff ( n ) аффинной группы Aff( n ) .

В этих определениях M — гладкое n -многообразие, а A = Aff( n )/GL( n ) — аффинное пространство той же размерности.

абсолютный

Пусть M — многообразие, а P главное GL( n ) -расслоение над M. — Тогда аффинная связность — это 1-форма η на P со значениями в aff ( n ) , удовлетворяющая следующим свойствам

1. η эквивариантно относительно действия GL( n ) на P и aff ( n ) ;
2. η ( X _ξ ) = ξ для всех ξ в алгебре Ли gl ( n ) всех матриц размера n × n ;
3. η — линейный изоморфизм каждого касательного пространства к P с aff ( n ) .

Последнее условие означает, что η является абсолютным параллелизмом на P , т. е. отождествляет касательное расслоение к P с тривиальным расслоением (в данном случае P × aff ( n ) ). Пара ( P , η ) определяет структуру аффинной геометрии на M , превращая ее в аффинное многообразие .

Аффинная алгебра Ли aff ( n ) распадается как полупрямое произведение R ^н и gl ( n ) , поэтому η можно записать в виде пары ( θ , ω ) , где θ принимает значения в R ^н и ω принимает значения в gl ( n ) . Условия 1 и 2 эквивалентны тому, ω является главной GL( n ) -связностью и θ является горизонтальной эквивариантной 1-формой, которая индуцирует гомоморфизм расслоения из TM что в ассоциированное расслоение P × _{GL( n )} R ^н . Условие 3 эквивалентно тому, что этот гомоморфизм расслоения является изоморфизмом. (Однако это разложение является следствием весьма специфической структуры аффинной группы.) Поскольку P — реперов расслоение P × _{GL( n )} R ^н , отсюда следует, что θ обеспечивает изоморфизм расслоения между P и расслоением фреймов F M из M ; восстанавливает определение аффинной связи как основной GL( n ) -связности на FM это .

1-формы, возникающие в плоской модели, представляют собой не что иное, как компоненты θ и ω .

Определение как главное аффинное соединение

Аффинная связность на M — это главное Aff( n ) -расслоение Q над M вместе с главным GL( n ) -подрасслоением P Q Aff и главным ( n ) -связностью α (1-форма на Q со значениями в aff ( n ) ), который удовлетворяет следующему (общему) условию Картана . Р ​ ^н Компонент обратного образа α в P определяет гомоморфизм расслоения из TM является горизонтальной эквивариантной 1-формой и, таким образом , в P × _{GL( n )} R ^н : это должно быть изоморфизмом.

Отношение к мотивации

Поскольку Aff( n ) действует на A , существует связанное с главным расслоением Q расслоение A = Q × _{Aff( n )} A , которое является расслоением над M , слой которого в точке x в M является аффинным пространством A _x . Сечение множества a A ) (определяющее отмеченную точку a _x в A _x для каждого M x ∈ определяет главное GL( n ) -подрасслоение P множества Q (как расслоение стабилизаторов этих отмеченных точек) и наоборот. Основное соединение α определяет соединение Эресмана на этом расслоении, отсюда и понятие параллельного транспорта. Условие Картана гарантирует, что выделенный участок a всегда движется параллельно.

Дальнейшие свойства

Кривизна и кручение

Кривизна и кручение — основные инварианты аффинной связности. Поскольку существует множество эквивалентных способов определения понятия аффинной связности, существует множество различных способов определения кривизны и кручения.

С точки зрения связи Картана, кривизна - это неспособность аффинной связи η удовлетворять уравнению Маурера – Картана.

$\mathrm {d} \eta +{\tfrac {1}{2}}[\eta \wedge \eta ]=0,$

где второй член в левой части — это клиновое произведение, использующее скобку Ли в aff ( n ) для сжатия значений. Разлагая η в пару ( θ , ω ) и используя структуру алгебры Ли aff ( n ) , эту левую часть можно разложить до двух формул:

$\mathrm {d} \theta +\omega \wedge \theta \quad {\text{and}}\quad \mathrm {d} \omega +\omega \wedge \omega \,,$

где произведения клина оцениваются с помощью матричного умножения. Первое выражение называется кручением связи, а второе еще называется кривизной.

Эти выражения являются дифференциальными 2-формами на всем пространстве расслоения реперов. Однако они горизонтальны и эквивариантны и, следовательно, определяют тензорные объекты. Их можно определить непосредственно из индуцированной ковариантной производной на TM следующим ∇ образом.

Кручение определяется формулой

$T^{\nabla }(X,Y)=\nabla _{X}Y-\nabla _{Y}X-[X,Y].$

Если кручение исчезает, то связь называется без кручения или симметричной .

Кривизна определяется формулой

$R_{X,Y}^{\nabla }Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z.$

Обратите внимание, что [ X , Y ] — скобка Ли векторных полей.

$[X,Y]=\left(X^{j}\partial _{j}Y^{i}-Y^{j}\partial _{j}X^{i}\right)\partial _{i}$

в обозначениях Эйнштейна . Это не зависит от выбора системы координат и

$\partial _{i}=\left({\frac {\partial }{\partial \xi ^{i}}}\right)_{p}\,,$

касательный вектор в точке p й i- координатной кривой . ∂i являются _X естественным базисом касательного пространства в точке p а , ^я соответствующие координаты векторного поля X = X ^я ∂ _i .

Когда и кривизна, и кручение исчезают, связность определяет структуру пре-алгебры Ли в пространстве глобальных сечений касательного расслоения.

Связь Леви-Чивита

Если ( M , g ) — риманово многообразие , то существует единственная аффинная связность ∇ на M со следующими двумя свойствами:

• соединение без кручения, т. е. T ^∇ равен нулю, так что ∇ _X Y − ∇ _Y X = [ X , Y ] ;
• параллельный транспорт является изометрией, т.е. скалярные произведения (определенные с помощью g ) между касательными векторами сохраняются.

Эта связь называется связью Леви-Чивита .

Термин «симметричный» часто используется вместо термина «без кручения» для первого свойства. Второе условие означает, что связность является метрической связностью в том смысле, что риманова метрика g параллельна: ∇ g = 0 . Для соединения без кручения условие эквивалентно тождеству X g ( Y , Z ) = g (∇ _X Y , Z ) + g ( Y , ∇ _X Z ) «совместимость с метрикой». В локальных координатах компоненты формы называются символами Кристоффеля : из-за единственности связи Леви-Чивиты существует формула для этих компонентов через компоненты g .

Геодезика

Поскольку прямые линии являются концепцией аффинной геометрии, аффинные связи определяют обобщенное понятие (параметризованных) прямых линий на любом аффинном многообразии, называемое аффинными геодезическими. Абстрактно, параметрическая кривая γ : I → M является прямой линией, если ее касательный вектор остается параллельным и равносильным самому себе при перемещении вдоль γ . С линейной точки зрения аффинная связность M отличает аффинные геодезические следующим образом: гладкая кривая γ : I → M является аффинной геодезической , если ${\dot {\gamma }}$ параллельно транспортируется вдоль γ , т.е.

$\tau _{t}^{s}{\dot {\gamma }}(s)={\dot {\gamma }}(t)$

где τ ^с
_t : T _{γ s} M → T _{γ t} M — карта параллельного транспорта, определяющая соединение.

В терминах бесконечно малой связи ∇ производная этого уравнения влечет за собой

$\nabla _{{\dot {\gamma }}(t)}{\dot {\gamma }}(t)=0$

для t ∈ I. всех

И наоборот, любое решение этого дифференциального уравнения дает кривую, касательный вектор которой параллельно перемещается вдоль кривой. Для каждого x ∈ M и каждого X ∈ T _x M существует единственная аффинная геодезическая γ : I → M такая, что γ (0) = x и γ̇ (0) = X , и где I — максимальный открытый интервал в R , содержащий 0, на котором определена геодезическая. Это следует из теоремы Пикара–Линделёфа и позволяет определить экспоненциальное отображение , связанное с аффинной связностью.

В частности, когда M — ( псевдо- ) риманово многообразие и ∇ — связность Леви-Чивита , то аффинные геодезические являются обычными геодезическими римановой геометрии и являются кривыми, минимизирующими локальное расстояние.

Определенные здесь геодезические иногда называют аффинно параметризованными , так как данная прямая в M определяет параметрическую кривую γ через прямую с точностью до выбора аффинной перепараметризации γ ( t ) → γ ( at + b ) , где a и b — константы . Касательный вектор к аффинной геодезической параллелен и равнополезен вдоль себя. Непараметризованная геодезическая или геодезическая, которая просто параллельна сама себе, но не обязательно является равноправной, должна только удовлетворять

$\nabla _{\dot {\gamma }}{\dot {\gamma }}=k{\dot {\gamma }}$

для некоторой функции k, определенной вдоль γ . Непараметрические геодезические часто изучаются с точки зрения проективных связностей .

Развитие

Аффинная связность определяет понятие развития кривых. Интуитивно, развитие отражает идею о том, что если x _t — кривая в M , то аффинное касательное пространство в точке x ₀ можно катить вдоль кривой. При этом отмеченная точка контакта между касательным пространством и многообразием очерчивает кривую в _Ct развитие xt _. этом аффинном пространстве :

Формально, пусть τ ⁰
_t : T _{x t} M → T _{x 0} M — линейно-параллельная транспортная карта, связанная с аффинным соединением. Тогда развитие C _t - кривая в T _{x 0} M начинается в 0 и параллельна касательной x _t в течение всего времени t :

${\dot {C}}_{t}=\tau _{t}^{0}{\dot {x}}_{t}\,,\quad C_{0}=0.$

В частности, x _t является геодезической тогда и только тогда, когда ее развертка представляет собой аффинно параметризованную прямую в T _{x 0} M .

поверхности

Если M — поверхность в R ³ , легко видеть, что M имеет естественную аффинную связность. С точки зрения линейной связи, ковариантная производная векторного поля определяется путем дифференцирования векторного поля, рассматриваемого как отображение от M до R. ³ , а затем ортогонально проецируем результат обратно на касательные пространства к M . Легко видеть, что эта аффинная связность не имеет кручения. Более того, это метрическая связность относительно римановой метрики на M , индуцированной скалярным произведением на R ³ , следовательно, это связность Леви-Чивита этой метрики.

Пример: единичная сфера в евклидовом пространстве

Пусть ⟨ , ⟩ — обычное скалярное произведение на R ³ , и пусть S ² быть единичной сферой. Касательное пространство к S ² в точке x естественным образом отождествляется с векторным подпространством R ³ состоящий из всех векторов, ортогональных x . Отсюда следует, что векторное поле Y на S ² можно рассматривать как карту Y : S ² → Р ³ который удовлетворяет

$\langle Y_{x},x\rangle =0\,,\quad \forall x\in \mathbf {S} ^{2}.$

Обозначим d Y дифференциал (матрицу Якобиана) такого отображения. Тогда у нас есть:

Лемма . Формула

$(\nabla _{Z}Y)_{x}=\mathrm {d} Y_{x}(Z_{x})+\langle Z_{x},Y_{x}\rangle x$

определяет аффинную связность на S ² с исчезающим кручением.

Доказательство . Непосредственно доказывается, что ∇ удовлетворяет тождеству Лейбница и является C ^∞ ( С ² ) линейный по первой переменной. Итак, все, что здесь нужно доказать, это то, что приведенная выше карта действительно определяет касательное векторное поле. То есть нам нужно доказать, что для всех x из S ²

${\bigl \langle }(\nabla _{Z}Y)_{x},x{\bigr \rangle }=0\,.\qquad {\text{(Eq.1)}}$

Рассмотрите карту

${\begin{aligned}f:\mathbf {S} ^{2}&\to \mathbf {R} \\x&\mapsto \langle Y_{x},x\rangle \,.\end{aligned}}$

Отображение f постоянно, следовательно, его дифференциал равен нулю. В частности

$\mathrm {d} f_{x}(Z_{x})={\bigl \langle }(\mathrm {d} Y)_{x}(Z_{x}),x(\gamma '(t)){\bigr \rangle }+\langle Y_{x},Z_{x}\rangle =0\,.$

Далее следует уравнение 1, приведенное выше. КЭД

См. также

• Атлас (топология)
• Связь (математика)
• Соединение (волоконный коллектор)
• Соединение (аффинный пакет)
• Дифференцируемое многообразие
• Дифференциальная геометрия
• Введение в математику общей теории относительности
• Связь Леви-Чивита
• Список формул римановой геометрии
• Риманова геометрия

Ссылки

• Акивис, Массачусетс; Розенфельд, Борис (1993). Элайджа Картон (1869–1951) . Перевод Гольдберга АМС В.В. ISBN  978-0-8218-5355-9 .
• Ли, Джон М. (1997). Римановы многообразия: введение в кривизну . Тексты для аспирантов по математике . Том. 176. Нью-Йорк: Springer-Verlag . ISBN  978-0-387-98322-6 . OCLC   54850593 .
• Ли, Джон М. (2018). Введение в римановы многообразия . Тексты для аспирантов по математике. Том. 176 (2-е изд.). Спрингер Издательство дои : 10.1007/978-3-319-91755-9 . ISBN  978-3-319-91755-9 .

Библиография

Основные исторические ссылки

• Кристоффель, Элвин Бруно (1869), «О преобразовании однородных дифференциальных выражений второй степени» , Журнал чистой и прикладной математики , 1869 (70): 46–70, doi : 10.1515/crll.1869.70.46 , S2CID   122999847
• Леви-Чивита, Туллио (1917), «Понятие параллелизма в любом многообразии и последующая геометрическая спецификация римановой кривизны» , Ренд. Цирк. Мэтт. Палермо , 42 : 173–205, номер документа : 10.1007/bf03014898 , S2CID   122088291.
• Картан, Эли (1923), «О многообразиях с аффинной связностью и теории обобщенной относительности (первая часть)», Annales Scientifiques de l'École Normale Supérieure , 40 : 325–412, doi : 10.24033/asens.751
• Картан, Эли (1924), «О многообразиях с аффинной связностью и теории обобщенной относительности (первая часть) (продолжение)», Annales Scientifiques de l'École Normale Supérieure , 41 : 1–25, doi : 10.24033/asens. 753
• Картан, Эли (1986), О многообразиях с аффинной связностью и общей теории относительности , Humanities Press

Рассмотрение Картаном аффинных связей мотивировано изучением теории относительности. Включает подробное обсуждение физики систем отсчета и того, как эта связь отражает физическое понятие транспорта по мировой линии .

• Картан, Эли (1926), «Пространства с аффинной, проективной и конформной связностью», Acta Math. , 48 :1–42, doi : 10.1007/BF02629755

Более математически мотивированное описание аффинных связей.

• Картан, Эли (1951), с приложениями Роберта Германа (ред.), Геометрия римановых пространств (перевод Джеймса Глейзбрука из лекций по геометрии римановых пространств , 2-е изд.), Math Sci Press, Массачусетс (опубликовано в 1983 г.), ISBN  978-0-915692-34-7 .

Аффинные связности с точки зрения римановой геометрии . В приложениях Роберта Германа обсуждаются мотивы теории поверхностей, а также понятие аффинных связей в современном смысле Кошуля. Он развивает основные свойства дифференциального оператора ∇ и связывает их с классическими аффинными связностями в смысле Картана.

• Вейль, Герман (1918), Raum, Zeit, Materie (5 изданий до 1922 г., с примечаниями Юргена Элерса (1980), перевод 4-го издания « Пространство, время, материя» Генри Броза, 1922 г. (Метуэн, переиздано в 1952 г. Дувром) изд. ), Шпрингер, Берлин, ISBN  0-486-60267-2

Вторичные ссылки

• Кобаяши, Шошичи; Номидзу, Кацуми (1996), Основы дифференциальной геометрии, Vols. 1 и 2 (новое издание), Wiley-Interscience, ISBN  0-471-15733-3 .

Это основная ссылка на технические детали статьи. Глава III тома 1 дает подробное описание аффинных связностей с точки зрения главных расслоений на многообразии, параллельного переноса, развития, геодезических и связанных с ними дифференциальных операторов. В главе VI тома 1 излагаются аффинные преобразования, кручение и общая теория аффинной геодезии. Во втором томе представлен ряд приложений аффинных связностей к однородным пространствам и комплексным многообразиям , а также к другим темам.

• Лумисте, Юло (2001a) [1994], «Аффинная связь» , в Хазевинкеле, Майкле (редактор), Энциклопедия математики , EMS Press , ISBN  978-1-55608-010-4 .
• Лумисте, Юло (2001b) [1994], «Соединения на многообразии» , в Хазевинкеле, Михеле (редактор), Энциклопедия математики , EMS Press , ISBN  978-1-55608-010-4 .

Две статьи Лумисте, дающие точные условия на параллельных транспортных картах для определения аффинных связей. Они также рассматривают кривизну, кручение и другие стандартные темы с классической точки зрения (неглавного расслоения).

• Шарп, RW (1997), Дифференциальная геометрия: обобщение Картаном программы Эрлангена Кляйна , Springer-Verlag, Нью-Йорк, ISBN  0-387-94732-9 .

Это дополняет некоторые исторические детали и дает более удобное для читателя элементарное описание связей Картана в целом. Приложение А поясняет взаимосвязь между точками зрения принципиальной связи и абсолютного параллелизма. Приложение B устраняет разрыв между классической «скользящей» моделью аффинных связностей и современной моделью, основанной на главных расслоениях и дифференциальных операторах.