Подключение (основной пакет)

В математике , и особенно в дифференциальной геометрии и калибровочной теории , соединение — это устройство, определяющее понятие параллельного переноса на связке; то есть способ «соединить» или идентифицировать волокна в близлежащих точках. Основная -связность G на главном G-расслоении $P$ над гладким многообразием $M$ это особый тип связи, который совместим с действием группы $G$ .

Основное соединение можно рассматривать как частный случай понятия соединения Эресмана , и его иногда называют основным соединением Эресмана . Это приводит к появлению (Эресмановских) связей на любом пучке волокон , связанном с $P$ через связанную конструкцию пучка . В частности, на любом ассоциированном векторном расслоении главная связь индуцирует ковариантную производную — оператор, который может дифференцировать секции этого расслоения по касательным направлениям в базовом многообразии. Главные связности обобщают на произвольные главные расслоения понятие линейной связности на расслоении реперов гладкого многообразия .

Формальное определение [ править ]

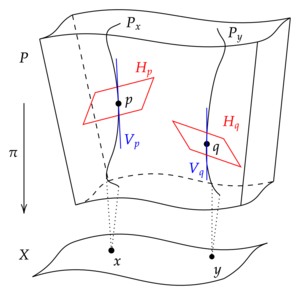
Позволять $\pi :P\to M$ — гладкое главное G -расслоение над гладким многообразием $M$ . Тогда директор $G$ -подключение включено $P$ является дифференциальной 1-формой на $P$ со значениями в алгебре Ли ${\mathfrak {g}}$ из $G$ который $G$ -эквивариантен и воспроизводит генераторы алгебры Ли фундаментальных векторных полей на $P$ .

Другими словами, это элемент ω из $\Omega ^{1}(P,{\mathfrak {g}})\cong C^{\infty }(P,T^{*}P\otimes {\mathfrak {g}})$ такой, что

${\hbox{Ad}}_{g}(R_{g}^{*}\omega )=\omega$ где $R_{g}$ обозначает правильное умножение на $g$ , и $\operatorname {Ad} _{g}$ является присоединенным представлением на ${\mathfrak {g}}$ (явно, $\operatorname {Ad} _{g}X={\frac {d}{dt}}g\exp(tX)g^{-1}{\bigl |}_{t=0}$ );
если $\xi \in {\mathfrak {g}}$ и $X_{\xi }$ — векторное поле на P, связанное с ξ путем дифференцирования действия G на P , тогда $\omega (X_{\xi })=\xi$ (идентично на $P$ ).

Иногда термин « принципал» $G$ -соединение относится к паре $(P,\omega )$ и $\omega$ сама называется формой связи или 1-формой связи главной связи.

Замечания по расчетам [ править ]

Наиболее известные нетривиальные вычисления принципала $G$ -связности осуществляются с однородными пространствами из-за тривиальности (ко)касательного расслоения. (Например, пусть $G\to H\to H/G$ , быть директором $G$ -связывать $H/G$ ) Это означает, что 1-формы на тотальном пространстве канонически изоморфны $C^{\infty }(H,{\mathfrak {g}}^{*})$ , где ${\mathfrak {g}}^{*}$ является двойственной алгеброй Ли, следовательно $G$ -связности находятся в биекции с $C^{\infty }(H,{\mathfrak {g}}^{*}\otimes {\mathfrak {g}})^{G}$ .

Связь с Ehresmann связями

Директор $G$ -связь $\omega$ на $P$ определяет связность Эресмана на $P$ следующим образом. Прежде всего отметим, что фундаментальные векторные поля, генерирующие $G$ действие по $P$ обеспечить изоморфизм расслоения (покрывающий тождество $P$ ) из комплекта $V$ к $P\times {\mathfrak {g}}$ , где $V=\ker(d\pi )$ является ядром касательного отображения ${\mathrm {d} }\pi \colon TP\to TM$ который называется вертикальным расслоением $P$ . Следует, что $\omega$ однозначно определяет карту пакета $v:TP\rightarrow V$ какая идентичность на $V$ . Такая проекция $v$ однозначно определяется своим ядром, которое представляет собой гладкое подрасслоение $H$ из $TP$ (называемый горизонтальным расслоением ) такой, что $TP=V\oplus H$ . Это связь Эресмана.

И наоборот, связность Эресмана $H\subset TP$ (или $v:TP\rightarrow V$ ) на $P$ определяет принципала $G$ -связь $\omega$ тогда и только тогда, когда это $G$ -эквивариантны в том смысле, что $H_{pg}=\mathrm {d} (R_{g})_{p}(H_{p})$ .

Отступите через раздел тривиализации [ править ]

Тривиализирующее сечение главного расслоения $P$ разделом s задается $P$ над открытым подмножеством $U$ из $M$ . Тогда откат s ^*ω главной связности является 1-формой на $U$ со значениями в ${\mathfrak {g}}$ . Если раздел s заменяется новым разделом sg , определяемым формулой ( sg )( x ) = s ( x ) g ( x ), где g : M → G — гладкое отображение, то $(sg)^{*}\omega =\operatorname {Ad} (g)^{-1}s^{*}\omega +g^{-1}dg$ . Основная связь однозначно определяется этим семейством ${\mathfrak {g}}$ -значные 1-формы, и эти 1-формы также называются формами соединения или 1-формами соединения , особенно в старой или более ориентированной на физику литературе.

Пакет основных соединений [ править ]

Группа $G$ действует на касательном расслоении $TP$ при правильном переводе. Факторпространство которое TP / G также является многообразием и наследует структуру расслоения над TM , будет обозначаться dπ : TP / G → TM . Пусть ρ: TP / G → M — проекция M. на Слои расслоения TP / G под проекцией ρ несут аддитивную структуру.

Расслоение TP / G называется расслоением главных связностей ( Кобаяши, 1957 ). Сечение такое , Γ dπ: TP / G → TM что Γ : TM → TP / G является линейным морфизмом векторных расслоений над M , можно отождествить с главной связностью в P . И наоборот, главная связь, определенная выше, порождает такое сечение Γ в TP / G .

Наконец, пусть Г — главная связность в этом смысле. Пусть q : TP → TP / G — фактор-отображение. Горизонтальное распределение связи – это пучок

H=q^{-1}\Gamma (TM)\subset TP.

Мы снова видим связь с горизонтальным расслоением и, следовательно, связность Эресмана.

Аффинное свойство [ править ]

Если ω и ω ′ — главные связности на главном расслоении P , то разность ω ′ − ω является ${\mathfrak {g}}$ -значная 1-форма на P , которая не только G -эквивариантна, но и горизонтальна в том смысле, что она обращается в нуль на любом сечении вертикального расслоения V поля P . Следовательно, он базовый и, следовательно, определяется 1-формой на M со значениями в присоединенном расслоении

{\mathfrak {g}}_{P}:=P\times ^{G}{\mathfrak {g}}.

И наоборот, любая такая форма определяет (посредством обратного образа) G -эквивариантную горизонтальную 1-форму на P , а пространство главных G -связностей является аффинным пространством для этого пространства 1-форм.

Примеры [ править ]

Связь Маурера-Картана [ править ]

Для тривиального принципала $G$ -пучок $\pi :E\to X$ где $E=G\times X$ , существует каноническая связь ^[1]^{стр. 49}

$\omega _{MC}\in \Omega ^{1}(E,{\mathfrak {g}})$

называется связью Маурера-Картана. Оно определяется следующим образом: для точки $(g,x)\in G\times X$ определять

$(\omega _{MC})_{(g,x)}=(L_{g^{-1}}\circ \pi _{1})_{*}$ для $x\in X,g\in G$

что представляет собой композиция

$T_{(g,x)}E\xrightarrow {\pi _{1*}} T_{g}G\xrightarrow {(L_{g^{-1}})_{*}} T_{e}G={\mathfrak {g}}$

определение 1-формы. Обратите внимание, что

$\omega _{0}=(L_{g^{-1}})_{*}:T_{g}G\to T_{e}G={\mathfrak {g}}$

является формой Маурера-Картана на группе Ли. $G$ и $\omega _{MC}=\pi _{1}^{*}\omega _{0}$ .

Тривиальный комплект [ править ]

Для тривиального принципала $G$ -пучок $\pi :E\to X$ , раздел личности $i:X\to G\times X$ данный $i(x)=i(e,x)$ определяет соответствие 1-1

$i^{*}:\Omega ^{1}(E,{\mathfrak {g}})\to \Omega ^{1}(X,{\mathfrak {g}})$

между соединениями на $E$ и ${\mathfrak {g}}$ -значные 1-формы на $X$ ^[1]^{стр. 53}. Для ${\mathfrak {g}}$ -значная 1-форма $A$ на $X$ , существует единственная 1-форма ${\tilde {A}}$ на $E$ такой, что

${\tilde {A}}(X)=0$ для $X\in T_{x}E$ вертикальный вектор
$R_{g}^{*}{\tilde {A}}={\text{Ad}}(g^{-1})\circ {\tilde {A}}$ для любого $g\in G$

Тогда, учитывая эту 1-форму, связность на $E$ можно построить, взяв сумму

$\omega _{MC}+{\tilde {A}}$

обеспечивая реальную связь на $E$ . Эту уникальную 1-форму можно построить, сначала рассматривая ее ограниченной $(e,x)$ для $x\in X$ . Затем, ${\tilde {A}}_{(e,x)}$ определяется $A$ потому что $T_{(x,e)}E=ker(\pi _{*})\oplus i_{*}T_{x}X$ и мы можем получить ${\tilde {A}}_{(g,x)}$ принимая

${\tilde {A}}_{(g,x)}=R_{g}^{*}{\tilde {A}}_{(e,x)}={\text{Ad}}(g^{-1})\circ {\tilde {A}}_{(e,x)}$

Аналогично, форма

${\tilde {A}}_{(x,g)}={\text{Ad}}(g^{-1})\circ A_{x}\circ \pi _{*}:T_{(x,g)}E\to {\mathfrak {g}}$

определяет 1-форму, дающую свойства 1 и 2, перечисленные выше.

Распространение этого на нетривиальные пакеты [ править ]

Это утверждение можно уточнить ^[1]^{стр. 55} еще дальше для нетривиальных расслоений $E\to X$ рассматривая открытое покрытие ${\mathcal {U}}=\{U_{a}\}_{a\in I}$ из $X$ с тривиализациями $\{\phi _{a}\}_{a\in I}$ и функции перехода $\{g_{ab}\}_{a,b\in I}$ . Тогда существует соответствие 1-1 между соединениями на $E$ и коллекции 1-форм

$\{A_{a}\in \Omega _{1}(U_{a},{\mathfrak {g}})\}_{a\in I}$

которые удовлетворяют

$A_{b}=Ad(g_{ab}^{-1})\circ A_{a}+g_{ab}^{*}\omega _{0}$

на перекрестках $U_{ab}$ для $\omega _{0}$ форма Маурера -Картана на $G$ , $\omega _{0}=g^{-1}dg$ в матричной форме.

Глобальная переформулировка пространства связей [ править ]

Для директора $G$ пучок $\pi :E\to M$ совокупность связей в $E$ это аффинное пространство ^[1]^{стр. 57} для векторного пространства $\Omega ^{1}(M,E_{\mathfrak {g}})$ где $E_{\mathfrak {g}}$ — ассоциированное векторное расслоение. Это означает, что для любых двух связей $\omega _{0},\omega _{1}$ существует форма $A\in \Omega ^{1}(M,E_{\mathfrak {g}})$ такой, что

$\omega _{0}=\omega _{1}+A$

Обозначим множество связей как ${\mathcal {A}}(E)$ , или просто ${\mathcal {A}}$ если контекст ясен.

Связь на комплексном расслоении Хопфа [ править ]

Мы ^[1]^{стр. 94} может построить $\mathbb {CP} ^{n}$ в качестве директора $\mathbb {C} ^{*}$ -пучок $\gamma :H_{\mathbb {C} }\to \mathbb {CP} ^{n}$ где $H_{\mathbb {C} }=\mathbb {C} ^{n+1}-\{0\}$ и $\gamma$ это карта проекции

$\gamma (z_{0},\ldots ,z_{n})=[z_{0},\ldots ,z_{n}]$

Обратите внимание на алгебру Ли $\mathbb {C} ^{*}=GL(1,\mathbb {C} )$ это просто сложная плоскость. 1-форма $\omega \in \Omega ^{1}(H_{\mathbb {C} },\mathbb {C} )$ определяется как

${\begin{aligned}\omega &={\frac {{\overline {z}}^{t}dz}{|z|^{2}}}\\&=\sum _{i=0}^{n}{\frac {{\overline {z}}_{i}}{|z|^{2}}}dz_{i}\end{aligned}}$

образует соединение, которое можно проверить, проверив определение. Для любого фиксированного $\lambda \in \mathbb {C} ^{*}$ у нас есть

${\begin{aligned}R_{\lambda }^{*}\omega &={\frac {{\overline {(z\lambda )}}^{t}d(z\lambda )}{|z\lambda |^{2}}}\\&={\frac {{\overline {\lambda }}\lambda {\overline {z}}^{t}dz}{|\lambda |^{2}\cdot |z|^{2}}}\end{aligned}}$

и с тех пор $|\lambda |^{2}={\overline {\lambda }}{\lambda }$ , у нас есть $\mathbb {C} ^{*}$ -инвариантность. Это связано с тем, что присоединенное действие тривиально, поскольку алгебра Ли абелева. Для построения разбиения обратите внимание на любое $z\in H_{\mathbb {C} }$ у нас есть короткая точная последовательность

$0\to \mathbb {C} \xrightarrow {v_{z}} T_{z}H_{\mathbb {Z} }\xrightarrow {\gamma _{*}} T_{[z]}\mathbb {CP} ^{n}\to 0$

где $v_{z}$ определяется как

$v_{z}(\lambda )=z\cdot \lambda$

поэтому он действует как масштабирование в волокне (что ограничивается соответствующим $\mathbb {C} ^{*}$ -действие). принимая $\omega _{z}\circ v_{z}(\lambda )$ мы получаем

${\begin{aligned}\omega _{z}\circ v_{z}(\lambda )&={\frac {{\overline {z}}dz}{|z|^{2}}}(z\lambda )\\&={\frac {{\overline {z}}z\lambda }{|z|^{2}}}\\&=\lambda \end{aligned}}$

откуда следует второе равенство, поскольку мы рассматриваем $z\lambda$ вертикальный касательный вектор и $dz(z\lambda )=z\lambda$ . Обозначения несколько сбивают с толку, но если мы расширим каждый термин

${\begin{aligned}dz&=dz_{0}+\cdots +dz_{n}\\z&=a_{0}z_{0}+\cdots +a_{n}z_{n}\\dz(z)&=a_{0}+\cdots +a_{n}\\dz(\lambda z)&=\lambda \cdot (a_{0}+\cdots +a_{n})\\{\overline {z}}&={\overline {a_{0}}}+\cdots +{\overline {a_{n}}}\end{aligned}}$

становится понятнее (где $a_{i}\in \mathbb {C}$ ).

ковариантные и внешние Индуцированные производные

Для любого линейного представления W группы G существует ассоциированное векторное расслоение $P\times ^{G}W$ над M , и главная связность индуцирует ковариантную производную на любом таком векторном расслоении. Эту ковариантную производную можно определить, используя тот факт, что пространство сечений $P\times ^{G}W$ над M изоморфно пространству G -эквивариантных W -значных функций на P . В более общем смысле, пространство k -форм со значениями в $P\times ^{G}W$ отождествляется с пространством G -эквивариантных и горизонтальных W -значных k -форм на P . Если α — такая k ее внешняя производная dα -форма, то , хотя и G -эквивариантна, уже не горизонтальна. Однако комбинация d α + ω Λ α такова. Это определяет внешнюю ковариантную производную d ^ой от $P\times ^{G}W$ -значные k -формы на M в $P\times ^{G}W$ -значные ( k +1)-формы на M . В частности, при k =0 мы получаем ковариантную производную по $P\times ^{G}W$ .

Форма кривизны [ править ]

Формой кривизны главной G -связности ω является ${\mathfrak {g}}$ -значная 2-форма Ω, определенная формулой

\Omega =d\omega +{\tfrac {1}{2}}[\omega \wedge \omega ].

Он G -эквивариантен и горизонтален, следовательно, соответствует 2-форме на M со значениями в ${\mathfrak {g}}_{P}$ . Отождествление кривизны с этой величиной иногда называют вторым структурным уравнением (Картана) . ^[2]Исторически появление структурных уравнений связано с развитием связи Картана . При переносе в контекст групп Ли структурные уравнения известны как уравнения Маурера-Картана : это одни и те же уравнения, но в другой настройке и обозначениях.

Плоские связи и характеристика жгутов с плоскими связями [ править ]

Мы говорим, что связь $\omega$ является плоским , если его форма кривизны $\Omega =0$ . Есть полезная характеристика главных расслоений с плоскими связностями; то есть главный $G$ -пучок $\pi :E\to X$ имеет плоское соединение ^[1]^{стр. 68} тогда и только тогда, когда существует открытое покрытие $\{U_{a}\}_{a\in I}$ с тривиализациями $\left\{\phi _{a}\right\}_{a\in I}$ такие, что все функции перехода

$g_{ab}:U_{a}\cap U_{b}\to G$

постоянны. Это полезно, поскольку дает рецепт построения плоского принципала. $G$ -расслоения на гладких многообразиях; а именно взять открытое покрытие и определить тривиализации с постоянными функциями перехода.

Соединения на связках рамы и кручение [ править ]

Если главный расслоение Р является каркасным расслоением или (более обобщенно) если оно имеет форму пайки , то соединение является примером аффинного соединения , и кривизна не является единственным инвариантом, поскольку дополнительная структура пайки образует θ , который является эквивариантом R ^н-значную 1-форму на P . В частности, форма кручения на P , является R ^н-значная 2-форма Θ, определенная формулой

\Theta =\mathrm {d} \theta +\omega \wedge \theta .

Θ G -эквивариантен и горизонтален, поэтому он спускается к касательной 2-форме на M , называемой кручением . Это уравнение иногда называют первым структурным уравнением (Картана) .

Определение в алгебраической геометрии [ править ]

Если X — это схема (или, в более общем смысле, стек, производный стек или даже предстек), мы можем связать с ним его так называемый стек де Рама , обозначаемый X _dR . Это свойство заключается в том, что главное расслоение G над X _dR — это то же самое, что и G с *плоской* связностью над X. расслоение

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж Дюпон, Йохан (август 2003 г.). «Пучки волокон и теория Черна-Вейля» (PDF) . Архивировано из оригинала (PDF) 31 марта 2022 года.
^ Эгучи, Тору; Гилки, Питер Б.; Хэнсон, Эндрю Дж. (1980). «Гравитация, калибровочные теории и дифференциальная геометрия» . Отчеты по физике . 66 (6): 213–393. Бибкод : 1980PhR....66..213E . дои : 10.1016/0370-1573(80)90130-1 .

Кобаяши, Шошичи (1957), «Теория связей», Ann. Мат. Приложение Пура. , 43 : 119–194, doi : 10.1007/BF02411907 , S2CID 120972987
Кобаяши, Шошичи; Номидзу, Кацуми (1996), Основы дифференциальной геометрии , том. 1 (Новое издание), Wiley Interscience , ISBN 0-471-15733-3
Коларж, Иван; Михор, Питер; Словак, Январь (1993), Естественные операции в дифференциальной геометрии (PDF) , Springer-Verlag, заархивировано из оригинала (PDF) 30 марта 2017 г. , получено 25 марта 2008 г.

[:0-1] Перейти обратно: ^а ^б ^с ^д ^Это ^ж Дюпон, Йохан (август 2003 г.). «Пучки волокон и теория Черна-Вейля» (PDF) . Архивировано из оригинала (PDF) 31 марта 2022 года.

[2] Эгучи, Тору; Гилки, Питер Б.; Хэнсон, Эндрю Дж. (1980). «Гравитация, калибровочные теории и дифференциальная геометрия» . Отчеты по физике . 66 (6): 213–393. Бибкод : 1980PhR....66..213E . дои : 10.1016/0370-1573(80)90130-1 .

[1]

[2]