Соединение (векторный пакет)

Эта статья о связях на векторных расслоениях. О других видах связей в математике см. Связь (математика) .

В математике , и особенно в дифференциальной геометрии и калибровочной теории , соединение на расслоении — это устройство, которое определяет понятие параллельного переноса на расслоении; то есть способ «соединить» или идентифицировать волокна в близлежащих точках. Наиболее распространенным случаем является линейное соединение векторного расслоения , для которого понятие параллельного транспорта должно быть линейным . Линейная связь эквивалентно задается ковариантной производной , оператором, который дифференцирует секции расслоения по касательным направлениям в базовом многообразии таким образом, что параллельные секции имеют нулевую производную. Линейные связи обобщают на произвольные векторные расслоения связность Леви-Чивита на касательном расслоении псевдориманова многообразия , что дает стандартный способ дифференцирования векторных полей. Нелинейные связи обобщают эту концепцию на расслоения, слои которых не обязательно линейны.

Линейные связи также называются связями Кошуля в честь Жана-Луи Кошуля , который дал алгебраическую основу для их описания ( Кошул 1950 ).

В этой статье определяется соединение векторного расслоения с использованием общепринятых математических обозначений, в которых координатам не уделяется должного внимания. Однако регулярно используются и другие обозначения: в общей теории относительности вычисления векторных расслоений обычно записываются с использованием индексированных тензоров; в калибровочной теории подчеркиваются эндоморфизмы слоев векторного пространства. Различные обозначения эквивалентны, как обсуждалось в статье о метрических связях (комментарии там относятся ко всем векторным расслоениям).

Мотивация

Пусть M — дифференцируемое многообразие , такое как евклидово пространство . Вектор-функция $M\to \mathbb {R} ^{n}$ можно рассматривать как сечение тривиального векторного расслоения $M\times \mathbb {R} ^{n}\to M.$ Можно рассматривать сечение общего дифференцируемого векторного расслоения, и поэтому естественно задаться вопросом, возможно ли дифференцировать сечение как обобщение того, как дифференцируют функцию на M .

Сечение расслоения можно рассматривать как обобщенную функцию от базы к слоям векторного расслоения. Это можно наглядно представить графиком сечения, как на рисунке выше.

Модельный случай – дифференцировать функцию $X:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ в евклидовом пространстве $\mathbb {R} ^{n}$. В этом случае производная $dX$ в какой-то момент $x\in \mathbb {R} ^{n}$ в направлении $v\in \mathbb {R} ^{n}$ может быть определен по стандартной формуле

$dX(v)(x)=\lim _{t\to 0}{\frac {X(x+tv)-X(x)}{t}}.$

Для каждого $x\in \mathbb {R} ^{n}$, это определяет новый вектор $dX(v)(x)\in \mathbb {R} ^{m}.$

При переходе в раздел $X$ векторного расслоения $E$ над многообразием $M$, в этом определении возникают две ключевые проблемы. Во-первых, поскольку многообразие не имеет линейной структуры, член $x+tv$ не имеет смысла $M$. Вместо этого человек идет по пути $\gamma :(-1,1)\to M$ такой, что $\gamma (0)=x,\gamma '(0)=v$ и вычисляет

$dX(v)(x)=\lim _{t\to 0}{\frac {X(\gamma (t))-X(\gamma (0))}{t}}.$

Однако это все еще не имеет смысла, поскольку $X(\gamma (t))$ и $X(\gamma (0))$ являются элементами различных векторных пространств $E_{\gamma (t)}$ и $E_{x}.$ Это означает, что вычитание этих двух членов не определено естественным образом.

Проблема решается введением дополнительной структуры связности в векторное расслоение . Есть по крайней мере три точки зрения, с которых можно понять связи. Если точно сформулировать, все три точки зрения эквивалентны.

1. ( Параллельная транспортировка ) Соединение можно рассматривать как присвоение каждому дифференцируемому пути. $\gamma$ изоморфизм линейный $P_{t}^{\gamma }:E_{\gamma (t)}\to E_{x}$ для всех $t.$ Используя этот изоморфизм, можно транспортировать $X(\gamma (t))$ к волокну $E_{x}$а затем возьмем разницу; явно,
   $$\nabla _{v}X=\lim _{t\to 0}{\frac {P_{t}^{\gamma }X(\gamma (t))-X(\gamma (0))}{t}}.$$
   Чтобы это зависело только от $v,$ и не по пути $\gamma$ расширение $v,$ необходимо наложить ограничения (в определении) на зависимость $P_{t}^{\gamma }$ на $\gamma .$Это непросто сформулировать, поэтому понятие «параллельной транспортировки» обычно возникает как побочный продукт других способов определения соединений. Фактически, следующее понятие «связности Эресмана» представляет собой не что иное, как бесконечно малую формулировку параллельного транспорта.
2. ( подключение Ehresmann ) Раздел $X$ можно рассматривать как гладкое отображение гладкого многообразия $M$ к гладкому многообразию $E.$ Таким образом, можно рассмотреть возможность продвижения вперед. $dX(v),$ который является элементом касательного пространства $T_{X(x)}E.$ В формулировке связи Эресманном каждый выбирает способ присвоения каждому $x$ и каждый $e\in E_{x},$ разложение в прямую сумму $T_{X(x)}E$ на два линейных подпространства, одно из которых является естественным вложением $E_{x}.$ С помощью этих дополнительных данных можно определить $\nabla _{v}X$ проецируя $dX(v)$ цениться в $E_{x}.$ Чтобы соблюдать линейную структуру векторного расслоения, накладываются дополнительные ограничения на то, как разложение в прямую сумму $T_{e}E$ движется при изменении e по волокну.
3. ( Ковариантная производная ) Стандартная производная $dX(v)$ в евклидовом контексте удовлетворяет определенным зависимостям от $X$ и $v,$самым фундаментальным из них является линейность. Ковариантной производной называется любая операция $(v,X)\mapsto \nabla _{v}X$ который имитирует эти свойства вместе с формой правила продукта .

Если база не является нульмерной, на данном дифференцируемом векторном расслоении всегда существует бесконечно много связей, и поэтому всегда существует соответствующий выбор того, как дифференцировать сечения. В зависимости от контекста могут быть различные варианты, например те, которые определяются путем решения определенных уравнений в частных производных . В случае касательного расслоения любая псевдориманова метрика (и, в частности, любая риманова метрика ) определяет каноническую связность, называемую связностью Леви-Чивита .

Формальное определение

Позволять $E\to M$ быть гладким действительным векторным расслоением над гладким многообразием $M$. Обозначим пространство участков гладких $E\to M$ к $\Gamma (E)$. Ковариантная производная от $E\to M$ представляет собой одну из следующих эквивалентных структур:

1. а $\mathbb {R}$- линейная карта $\nabla :\Gamma (E)\to \Gamma (T^{*}M\otimes E)$ такое, что правило произведения
   $$\nabla (fs)=df\otimes s+f\nabla s$$
   справедливо для всех гладких функций $f$ на $M$ и все гладкие участки $s$ из $E.$
2. присваивание любому гладкому сечению и каждому $x\in M$, из $\mathbb {R}$-линейная карта $(\nabla s)_{x}:T_{x}M\to E_{x}$ которая гладко зависит от x и такая, что
   $$\nabla (a_{1}s_{1}+a_{2}s_{2})=a_{1}\nabla s_{1}+a_{2}\nabla s_{2}$$
   для любых двух гладких участков $s_{1},s_{2}$ и любые действительные числа $a_{1},a_{2},$ и такой, что для любой гладкой функции $f$, $\nabla (fs)$ относится к $\nabla s$ к
   $${\big (}\nabla (fs){\big )}_{x}(v)=df(v)s(x)+f(x)(\nabla s)_{x}(v)$$
   для любого $x\in M$ и $v\in T_{x}M.$

Помимо использования канонической идентификации между векторным пространством $T_{x}^{\ast }M\otimes E_{x}$ и векторное пространство линейных отображений $T_{x}M\to E_{x},$ эти два определения идентичны и различаются только используемым языком.

Характерно обозначать $(\nabla s)_{x}(v)$ к $\nabla _{v}s,$ с $x$ будучи неявным в $v.$ С такими обозначениями правило произведения во второй версии приведенного выше определения записывается

$\nabla _{v}(fs)=df(v)s+f\nabla _{v}s.$

Замечание. В случае комплексного векторного расслоения приведенное выше определение по-прежнему имеет смысл, но обычно его модифицируют путем замены «реальных» и «реальных». $\mathbb {R}$"везде они кажутся "сложными" и " $\mathbb {C} .$«Это накладывает дополнительные ограничения, поскольку не каждое вещественно-линейное отображение между комплексными векторными пространствами является комплексно-линейным. В этом различии есть некоторая двусмысленность, поскольку комплексное векторное расслоение также можно рассматривать как вещественное векторное расслоение.

Индуцированные связи

Учитывая векторное расслоение $E\to M$, существует множество связанных пакетов для $E$ которое может быть построено, например, двойственное векторное расслоение $E^{*}$, тензорные степени $E^{\otimes k}$, симметричные и антисимметричные тензорные степени $S^{k}E,\Lambda ^{k}E$, а прямые суммы $E^{\oplus k}$. Соединение включено $E$индуцирует соединение в любом из этих связанных расслоений. Легкость перехода между связями в ассоциированных расслоениях более элегантно фиксируется теорией главных связей расслоений , но здесь мы представляем некоторые основные индуцированные связи.

Двойное соединение

Данный $\nabla$ соединение на $E$, индуцированная двойственная связность $\nabla ^{*}$ на $E^{*}$ определяется неявно

$d(\langle \xi ,s\rangle )(X)=\langle \nabla _{X}^{*}\xi ,s\rangle +\langle \xi ,\nabla _{X}s\rangle .$

Здесь $X\in \Gamma (TM)$ — гладкое векторное поле, $s\in \Gamma (E)$ это раздел $E$, и $\xi \in \Gamma (E^{*})$ часть двойного пучка, и $\langle \cdot ,\cdot \rangle$ естественное спаривание векторного пространства и его двойника (происходящее на каждом слое между $E$ и $E^{*}$), то есть, $\langle \xi ,s\rangle :=\xi (s)$. Обратите внимание, что это определение, по сути, подтверждает, что $\nabla ^{*}$ быть связью $E^{*}$ правило натурального продукта так что для спаривания соблюдается $\langle \cdot ,\cdot \rangle$.

Подключение тензорного продукта

Данный $\nabla ^{E},\nabla ^{F}$ связи на двух векторных расслоениях $E,F\to M$, определим связь тензорного произведения по формуле

$(\nabla ^{E}\otimes \nabla ^{F})_{X}(s\otimes t)=\nabla _{X}^{E}(s)\otimes t+s\otimes \nabla _{X}^{F}(t).$

Здесь у нас есть $s\in \Gamma (E),t\in \Gamma (F),X\in \Gamma (TM)$. Еще раз заметьте, что это естественный способ объединения $\nabla ^{E},\nabla ^{F}$чтобы обеспечить соблюдение правила произведения для соединения тензорного произведения. Путем повторного применения приведенной выше конструкции к тензорному произведению $E^{\otimes k}=(E^{\otimes (k-1)})\otimes E$, также получается тензорная степенная связность на $E^{\otimes k}$ для любого $k\geq 1$ и векторное расслоение $E$.

Прямое соединение суммы

Связь прямой суммы определяется формулой

$(\nabla ^{E}\oplus \nabla ^{F})_{X}(s\oplus t)=\nabla _{X}^{E}(s)\oplus \nabla _{X}^{F}(t),$

где $s\oplus t\in \Gamma (E\oplus F)$.

подключения питания

Поскольку симметричную степень и внешнюю степень векторного расслоения можно естественным образом рассматривать как подпространства тензорной степени, $S^{k}E,\Lambda ^{k}E\subset E^{\otimes k}$, определение связи тензорного произведения напрямую применимо к этой настройке. Действительно, поскольку симметрическая и внешняя алгебры находятся внутри тензорной алгебры как прямые слагаемые, и связь $\nabla$ соблюдая это естественное разделение, можно просто ограничить $\nabla$к этим слагаемым. Явно определите симметричное соединение продукта с помощью

$\nabla _{X}^{\odot 2}(s\cdot t)=\nabla _{X}s\odot t+s\odot \nabla _{X}t$

и внешнее соединение продукта с помощью

$\nabla _{X}^{\wedge 2}(s\wedge t)=\nabla _{X}s\wedge t+s\wedge \nabla _{X}t$

для всех $s,t\in \Gamma (E),X\in \Gamma (TM)$. Повторное применение этих продуктов обеспечивает наведенную симметричную мощность и внешние силовые соединения на $S^{k}E$ и $\Lambda ^{k}E$ соответственно.

эндоморфизма

Наконец, можно определить индуцированную связь $\nabla ^{\operatorname {End} {E}}$ на векторном расслоении эндоморфизмов $\operatorname {End} (E)=E^{*}\otimes E$, эндоморфизм связи . Это просто тензорное произведение двойной связи. $\nabla ^{*}$ на $E^{*}$ и $\nabla$ на $E$. Если $s\in \Gamma (E)$ и $u\in \Gamma (\operatorname {End} (E))$, так что композиция $u(s)\in \Gamma (E)$ кроме того, для связи эндоморфизма справедливо следующее правило произведения:

$\nabla _{X}(u(s))=\nabla _{X}^{\operatorname {End} (E)}(u)(s)+u(\nabla _{X}(s)).$

Обращая это уравнение, можно определить связь эндоморфизма как уникальную связь, удовлетворяющую

$\nabla _{X}^{\operatorname {End} (E)}(u)(s)=\nabla _{X}(u(s))-u(\nabla _{X}(s))$

для любого $u,s,X$, что позволяет избежать необходимости сначала определять двойную связь и связь тензорного произведения.

Любой связанный пакет

См. также: Подключение (основной пакет)

Учитывая векторное расслоение $E$ ранга $r$и любое представление $\rho :\mathrm {GL} (r,\mathbb {K} )\to G$ в линейную группу $G\subset \mathrm {GL} (V)$, на ассоциированном векторном расслоении существует индуцированная связность $F=E\times _{\rho }V$. Эту теорию наиболее кратко можно выразить, перейдя к связности главного расслоения на расслоении фреймов $E$и используя теорию главных расслоений. Каждый из приведенных выше примеров можно рассматривать как частный случай этой конструкции: двойственное расслоение соответствует обратному транспонированному (или обратному присоединенному) представлению, тензорное произведение — представлению тензорного произведения, прямая сумма — представлению прямой суммы и, таким образом, на.

векторнозначные

См. Также: Внешняя ковариантная производная.

Позволять $E\to M$быть векторным расслоением. Ан $E$-значная дифференциальная форма степени $r$ — это часть пакета тензорных произведений :

$\bigwedge ^{r}T^{*}M\otimes E.$

Пространство таких форм обозначается

$\Omega ^{r}(E)=\Omega ^{r}(M;E)=\Gamma \left(\bigwedge ^{r}T^{*}M\otimes E\right)=\Omega ^{r}(M)\otimes _{C^{\infty }(M)}\Gamma (E),$

где последнее тензорное произведение обозначает тензорное произведение модулей по кольцу гладких функций на $M$.

Ан $E$-значная 0-форма — это всего лишь часть расслоения $E$. То есть,

$\Omega ^{0}(E)=\Gamma (E).$

В этих обозначениях связь на $E\to M$ это линейная карта

$\nabla :\Omega ^{0}(E)\to \Omega ^{1}(E).$

Тогда связь можно рассматривать как обобщение внешней производной на формы со значениями векторного расслоения. Действительно, учитывая связь $\nabla$ на $E$ есть уникальный способ продлить $\nabla$ к внешней ковариантной производной

$d_{\nabla }:\Omega ^{r}(E)\to \Omega ^{r+1}(E).$

Эта внешняя ковариантная производная определяется следующим правилом Лейбница, которое указано для простых тензоров вида $\omega \otimes s$ и продолжено линейно:

$d_{\nabla }(\omega \otimes s)=d\omega \otimes s+(-1)^{\deg \omega }\omega \wedge \nabla s$

где $\omega \in \Omega ^{r}(M)$ так что $\deg \omega =r$, $s\in \Gamma (E)$ это раздел, и $\omega \wedge \nabla s$ обозначает $(r+1)$-форма со значениями в $E$ определяется расклиниванием $\omega$ с одноформной частью $\nabla s$. Обратите внимание, что для $E$-значные 0-формы, это восстанавливает нормальное правило Лейбница для связи $\nabla$.

В отличие от обычной внешней производной, обычно имеется $d_{\nabla }^{2}\neq 0$. Фактически, $d_{\nabla }^{2}$ напрямую связано с кривизной соединения $\nabla$ (см. ниже ).

Аффинные свойства набора связей

Каждое векторное расслоение над многообразием допускает связность, которую можно доказать с помощью разбиений единицы . Однако связи не уникальны. Если $\nabla _{1}$ и $\nabla _{2}$ есть два соединения $E\to M$ тогда их разница $C^{\infty }(M)$-линейный оператор. То есть,

$(\nabla _{1}-\nabla _{2})(fs)=f(\nabla _{1}s-\nabla _{2}s)$

для всех плавных функций $f$ на $M$ и все гладкие участки $s$ из $E$. Отсюда следует, что разница $\nabla _{1}-\nabla _{2}$ может быть однозначно идентифицирован с помощью одной формы на $M$ со значениями в расслоении эндоморфизмов $\operatorname {End} (E)=E^{*}\otimes E$:

$\nabla _{1}-\nabla _{2}\in \Omega ^{1}(M;\mathrm {End} \,E).$

И наоборот, если $\nabla$ это соединение на $E$ и $A$ представляет собой одну форму на $M$ со значениями в $\operatorname {End} (E)$, затем $\nabla +A$ это соединение на $E$.

Другими словами, пространство связей на $E$ является аффинным пространством для $\Omega ^{1}(\operatorname {End} (E))$. Это аффинное пространство обычно обозначается ${\mathcal {A}}$.

Отношение к принципалу и

Позволять $E\to M$ быть векторным расслоением ранга $k$ и разреши ${\mathcal {F}}(E)$ быть кадров набором $E$. Тогда (главное) соединение на ${\mathcal {F}}(E)$ вызывает связь на $E$. Прежде всего отметим, что разделы $E$ находятся во взаимно однозначном соответствии с правоэквивариантными отображениями ${\mathcal {F}}(E)\to \mathbb {R} ^{k}$. рассматривая откат (Это можно увидеть , $E$ над ${\mathcal {F}}(E)\to M$, изоморфное тривиальному расслоению ${\mathcal {F}}(E)\times \mathbb {R} ^{k}$.) Учитывая раздел $s$ из $E$ пусть соответствующее эквивариантное отображение будет $\psi (s)$. Ковариантная производная по $E$ затем дается

$\psi (\nabla _{X}s)=X^{H}(\psi (s))$

где $X^{H}$ это подъем горизонтальный $X$ от $M$ к ${\mathcal {F}}(E)$. (Напомним, что горизонтальный подъем определяется соединением на ${\mathcal {F}}(E)$.)

И наоборот, соединение на $E$ определяет соединение на ${\mathcal {F}}(E)$, и эти две конструкции взаимно обратны.

Соединение включено $E$ также определяется эквивалентно линейной связностью Эресмана на $E$. Это предоставляет один метод для создания связанного основного соединения.

Индуцированные соединения, обсуждаемые в разделе #Индуцированные соединения, могут быть построены как соединения других связанных пакетов с пакетом кадров $E$, используя представления, отличные от стандартного представления, использованного выше. Например, если $\rho$ обозначает стандартное представление $\operatorname {GL} (k,\mathbb {R} )$ на $\mathbb {R} ^{k}$, то соответствующий расслоение представлению $\rho \oplus \rho$ из $\operatorname {GL} (k,\mathbb {R} )$ на $\mathbb {R} ^{k}\oplus \mathbb {R} ^{k}$ это расслоение прямой суммы $E\oplus E$, а индуцированная связь – это именно та, которая была описана выше.

Местное выражение

Позволять $E\to M$ быть векторным расслоением ранга $k$, и разреши $U$ быть открытым подмножеством $M$ в течение которого $E$упрощает. Поэтому за множество $U$, $E$ допускает локальный гладкий каркас сечений

$\mathbf {e} =(e_{1},\dots ,e_{k});\quad e_{i}:U\to \left.E\right|_{U}.$

Начиная с кадра $\mathbf {e}$ определяет основу волокна $E_{x}$ для любого $x\in U$, можно расширить любой локальный раздел $s:U\to \left.E\right|_{U}$ в кадре как

$s=\sum _{i=1}^{k}s^{i}e_{i}$

для набора гладких функций $s^{1},\dots ,s^{k}:U\to \mathbb {R}$.

Учитывая связь $\nabla$ на $E$, можно выразить $\nabla$ над $U$в рамках локального каркаса разделов, используя для связи правило характеристического произведения. Для любого раздела базы $e_{i}$, количество $\nabla (e_{i})\in \Omega ^{1}(U)\otimes \Gamma (U,E)$ может быть расширен в локальном фрейме $\mathbf {e}$ как

$\nabla (e_{i})=\sum _{j=1}^{k}A_{i}^{\ j}\otimes e_{j},$

где $A_{i}^{\ j}\in \Omega ^{1}(U);\,j=1,\dots ,k$представляют собой совокупность локальных одноформ. Эти формы можно поместить в матрицу одноформ, определяемую формулой

$A={\begin{pmatrix}A_{1}^{\ 1}&\cdots &A_{k}^{\ 1}\\\vdots &\ddots &\vdots \\A_{1}^{\ k}&\cdots &A_{k}^{\ k}\end{pmatrix}}\in \Omega ^{1}(U,\operatorname {End} (\left.E\right|_{U}))$

называется формой локального соединения $\nabla$ над $U$. Действие $\nabla$ в любом разделе $s:U\to \left.E\right|_{U}$ можно вычислить с точки зрения $A$ используя правило продукта как

$\nabla (s)=\sum _{j=1}^{k}\left(ds^{j}+\sum _{i=1}^{k}A_{i}^{\ j}s^{i}\right)\otimes e_{j}.$

Если локальный раздел $s$ также записывается в матричной записи как вектор-столбец с использованием локальной системы отсчета $\mathbf {e}$ в качестве основы,

$s={\begin{pmatrix}s^{1}\\\vdots \\s^{k}\end{pmatrix}},$

тогда, используя обычное матричное умножение, можно написать

$\nabla (s)=ds+As$

где $ds$ это сокращение для применения внешней производной $d$ каждому компоненту $s$как вектор-столбец. В этих обозначениях локально часто пишут, что $\left.\nabla \right|_{U}=d+A$. В этом смысле соединение локально полностью определяется своей одной формой соединения в некоторой тривиализации.

Как объяснено в разделе #Аффинные свойства набора соединений , любое соединение отличается от другого одной формой со значением эндоморфизма. С этой точки зрения связь одноформная $A$ есть в точности одноформа со значениями эндоморфизмов такая, что связность $\left.\nabla \right|_{U}$ на $\left.E\right|_{U}$ отличается от тривиальной связи $d$ на $\left.E\right|_{U}$, который существует потому, что $U$ является тривиализирующим множеством для $E$.

символами

В псевдоримановой геометрии связь Леви -Чивита часто записывают в терминах символов Кристоффеля. $\Gamma _{ij}^{\ \ k}$ вместо соединения одноформовое $A$. Символы Кристоффеля для связности можно определить на любом векторном расслоении, а не только на касательном расслоении псевдориманова многообразия. Для этого предположим, что помимо $U$ будучи тривиализирующим открытым подмножеством векторного расслоения $E\to M$, что $U$ также является локальной картой многообразия $M$, допуская локальные координаты $\mathbf {x} =(x^{1},\dots ,x^{n});\quad x^{i}:U\to \mathbb {R}$.

В такой локальной карте существует выделенная локальная система отсчета для дифференциальных форм, заданная формулой $(dx^{1},\dots ,dx^{n})$, а единица локальной связи $A_{i}^{j}$ можно расширить на этой основе как

$A_{i}^{\ j}=\sum _{\ell =1}^{n}\Gamma _{\ell i}^{\ \ j}dx^{\ell }$

для набора локальных гладких функций $\Gamma _{\ell i}^{\ \ j}:U\to \mathbb {R}$, называемые Кристоффеля символами $\nabla$ над $U$. В случае, когда $E=TM$ и $\nabla$ является связью Леви-Чивита, эти символы точно согласуются с символами Кристоффеля из псевдоримановой геометрии.

Выражение о том, как $\nabla$ действия в локальных координатах могут быть дополнительно расширены с точки зрения локальной карты $U$ и символы Кристоффеля, которые будут заданы

$\nabla (s)=\sum _{i,j=1}^{k}\sum _{\ell =1}^{n}\left({\frac {\partial s^{j}}{\partial x^{\ell }}}+\Gamma _{\ell i}^{\ \ j}s^{i}\right)dx^{\ell }\otimes e_{j}.$

Сокращение этого выражения с помощью касательного вектора локальной координаты ${\frac {\partial }{\partial x^{\ell }}}$ приводит к

$\nabla _{\frac {\partial }{\partial x^{\ell }}}(s)=\sum _{i,j=1}^{k}\left({\frac {\partial s^{j}}{\partial x^{\ell }}}+\Gamma _{\ell i}^{\ \ j}s^{i}\right)e_{j}.$

Это определяет набор $n$ локально определенные операторы

$\nabla _{\ell }:\Gamma (U,E)\to \Gamma (U,E);\quad \nabla _{\ell }(s):=\sum _{i,j=1}^{k}\left({\frac {\partial s^{j}}{\partial x^{\ell }}}+\Gamma _{\ell i}^{\ \ j}s^{i}\right)e_{j},$

с имуществом, которое

$\nabla (s)=\sum _{\ell =1}^{n}dx^{\ell }\otimes \nabla _{\ell }(s).$

Изменение локальной тривиализации

Предполагать $\mathbf {e'}$ это другой выбор локального фрейма на том же тривиализирующем множестве $U$, так что существует матрица $g=(g_{i}^{\ j})$ гладких функций, касающихся $\mathbf {e}$ и $\mathbf {e'}$, определяется

$e_{i}=\sum _{j=1}^{k}g_{i}^{\ j}e'_{j}.$

Трассировка через построение формы локального подключения $A$ для рамки $\mathbf {e}$, обнаруживается, что связь имеет одну форму $A'$ для $\mathbf {e'}$ дан кем-то

${A'}_{i}^{\ j}=\sum _{p,q=1}^{k}g_{p}^{\ j}A_{q}^{\ p}{(g^{-1})}_{i}^{\ q}-\sum _{p=1}^{k}(dg)_{p}^{\ j}{(g^{-1})}_{i}^{\ p}$

где $g^{-1}=\left({(g^{-1})}_{i}^{\ j}\right)$ обозначает обратную матрицу к $g$. В матричной записи это можно записать

$A'=gAg^{-1}-(dg)g^{-1}$

где $dg$ - матрица одноформ, заданная путем взятия внешней производной матрицы $g$ покомпонентно.

В случае, когда $E=TM$ представляет собой касательное расслоение и $g$ является якобианом координатного преобразования $M$, длинные формулы преобразования символов Кристоффеля связи Леви-Чивита могут быть восстановлены из более кратких законов преобразования формы связи, приведенной выше.

транспорт

Связь $\nabla$ на векторном расслоении $E\to M$ определяет понятие параллельного транспорта на $E$ по кривой в $M$. Позволять $\gamma :[0,1]\to M$ быть гладким путем в $M$. Секция $s$ из $E$ вдоль $\gamma$ называется параллельным , если

$\nabla _{{\dot {\gamma }}(t)}s=0$

для всех $t\in [0,1]$. Эквивалентно можно рассмотреть расслоение откатов $\gamma ^{*}E$ из $E$ к $\gamma$. Это векторное расслоение над $[0,1]$ с волокном $E_{\gamma (t)}$ над $t\in [0,1]$. Связь $\nabla$ на $E$ возвращается к соединению $\gamma ^{*}E$. Секция $s$ из $\gamma ^{*}E$ параллельно тогда и только тогда, когда $\gamma ^{*}\nabla (s)=0$.

Предполагать $\gamma$ это путь из $x$ к $y$ в $M$. Приведенное выше уравнение, определяющее параллельные секции, представляет собой обыкновенное дифференциальное уравнение первого порядка (см. Локальное выражение выше) и поэтому имеет единственное решение для каждого возможного начального условия. То есть для каждого вектора $v$ в $E_{x}$ существует уникальный параллельный участок $s$ из $\gamma ^{*}E$ с $s(0)=v$. Определить параллельную транспортную карту

$\tau _{\gamma }:E_{x}\to E_{y}\,$

к $\tau _{\gamma }(v)=s(1)$. Можно показать, что $\tau _{\gamma }$ является линейным изоморфизмом , обратный путь которого задается той же процедурой, что и обратный путь $\gamma ^{-}$ от $y$ к $x$.

Как восстановить ковариантную производную соединения из его параллельного транспорта. Ценности $s(\gamma (t))$ раздела $s\in \Gamma (E)$ параллельно транспортируются по пути $\gamma$ вернуться к $\gamma (0)=x$, а затем ковариантная производная берется в фиксированном векторном пространстве, слое $E_{x}$ над $x$.

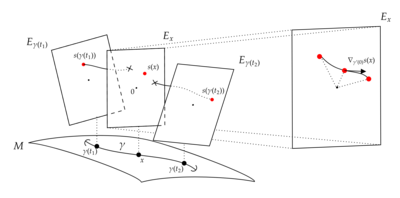
Параллельная транспортировка может использоваться для определения группы голономии соединения. $\nabla$ основанный на точке $x$ в $M$. Это подгруппа $\operatorname {GL} (E_{x})$ состоящий из всех параллельных транспортных карт, поступающих из циклов , основанных на $x$:

$\mathrm {Hol} _{x}=\{\tau _{\gamma }:\gamma {\text{ is a loop based at }}x\}.\,$

Группа голономии связи тесно связана с кривизной связи ( AmbroseSinger 1953 ).

Соединение можно восстановить от его параллельных транспортных операторов следующим образом. Если $X\in \Gamma (TM)$ является векторным полем и $s\in \Gamma (E)$ раздел, в какой-то момент $x\in M$ выбрать интегральную кривую $\gamma :(-\varepsilon ,\varepsilon )\to M$ для $X$ в $x$. Для каждого $t\in (-\varepsilon ,\varepsilon )$ мы напишем $\tau _{t}:E_{\gamma (t)}\to E_{x}$ для параллельной транспортной карты, идущей по $\gamma$ от $t$ к $0$. В частности, для каждого $t\in (-\varepsilon ,\varepsilon )$, у нас есть $\tau _{t}s(\gamma (t))\in E_{x}$. Затем $t\mapsto \tau _{t}s(\gamma (t))$ определяет кривую в векторном пространстве $E_{x}$, которые можно дифференцировать. Ковариантная производная восстанавливается как

$\nabla _{X}s(x)={\frac {d}{dt}}\left(\tau _{t}s(\gamma (t))\right)_{t=0}.$

Это демонстрирует, что эквивалентное определение соединения дается путем указания всех параллельных транспортных изоморфизмов. $\tau _{\gamma }$ между волокнами $E$ и принимая приведенное выше выражение в качестве определения $\nabla$.

Кривизна

См. Также: Форма кривизны.

Кривизна ​ соединения $\nabla$ на $E\to M$ это 2-форма $F_{\nabla }$ на $M$ со значениями в расслоении эндоморфизмов $\operatorname {End} (E)=E^{*}\otimes E$. То есть,

$F_{\nabla }\in \Omega ^{2}(\mathrm {End} (E))=\Gamma (\Lambda ^{2}T^{*}M\otimes \mathrm {End} (E)).$

Оно определяется выражением

$F_{\nabla }(X,Y)(s)=\nabla _{X}\nabla _{Y}s-\nabla _{Y}\nabla _{X}s-\nabla _{[X,Y]}s$

где $X$ и $Y$ являются касательными векторными полями на $M$ и $s$ это раздел $E$. Это надо проверить $F_{\nabla }$ является $C^{\infty }(M)$-линейный в обоих случаях $X$ и $Y$ и что он фактически определяет эндоморфизм расслоения $E$.

Как упоминалось выше , ковариантная внешняя производная $d_{\nabla }$ не обязательно приводить к нулю при воздействии на $E$-значные формы. Оператор $d_{\nabla }^{2}$ однако является строго тензорным (т.е. $C^{\infty }(M)$-линейный). Это означает, что оно индуцировано из 2-формы со значениями в $\operatorname {End} (E)$. Эта 2-форма представляет собой в точности форму кривизны, приведенную выше. Для $E$-значная форма $\sigma$ у нас есть

$(d_{\nabla })^{2}\sigma =F_{\nabla }\wedge \sigma .$

Плоское соединение — это соединение, форма кривизны которого тождественно равна нулю.

Картана

Форма кривизны имеет локальное описание, называемое структурным уравнением Картана . Если $\nabla$ имеет локальную форму $A$ на некотором тривиализирующем открытом подмножестве $U\subset M$ для $E$, затем

$F_{\nabla }=dA+A\wedge A$

на $U$. Для пояснения этого обозначения заметим, что $A$является одноформой со значением эндоморфизма и поэтому в локальных координатах принимает форму матрицы одноформ. Операция $d$ применяет внешнюю производную покомпонентно к этой матрице и $A\wedge A$ обозначает матричное умножение, при котором компоненты объединяются, а не умножаются.

В местных координатах $\mathbf {x} =(x^{1},\dots ,x^{n})$ на $M$ над $U$, если в форме подключения написано $A=A_{\ell }dx^{\ell }=(\Gamma _{\ell i}^{\ \ j})dx^{\ell }$ для набора локальных эндоморфизмов $A_{\ell }=(\Gamma _{\ell i}^{\ \ j})$, то есть

$F_{\nabla }=\sum _{p,q=1}^{n}{\frac {1}{2}}\left({\frac {\partial A_{q}}{\partial x^{p}}}-{\frac {\partial A_{p}}{\partial x^{q}}}+[A_{p},A_{q}]\right)dx^{p}\wedge dx^{q}.$

Дальнейшее расширение этого с точки зрения символов Кристоффеля. $\Gamma _{\ell i}^{\ \ j}$дает знакомое выражение из римановой геометрии. А именно, если $s=s^{i}e_{i}$ это раздел $E$ над $U$, затем

$F_{\nabla }(s)=\sum _{i,j=1}^{k}\sum _{p,q=1}^{n}{\frac {1}{2}}\left({\frac {\partial \Gamma _{qi}^{\ \ j}}{\partial x^{p}}}-{\frac {\partial \Gamma _{pi}^{\ \ j}}{\partial x^{q}}}+\Gamma _{pr}^{\ \ j}\Gamma _{qi}^{\ \ r}-\Gamma _{qr}^{\ \ j}\Gamma _{pi}^{\ \ r}\right)s^{i}dx^{p}\wedge dx^{q}\otimes e_{j}=\sum _{i,j=1}^{k}\sum _{p,q=1}^{n}R_{pqi}^{\ \ \ j}s^{i}dx^{p}\wedge dx^{q}\otimes e_{j}.$

Здесь $R=(R_{pqi}^{\ \ \ j})$ полной кривизны тензор $F_{\nabla }$, а в римановой геометрии будет отождествляться с тензором римановой кривизны .

Можно проверить, что если мы определим $[A,A]$ быть клиновым произведением форм, но коммутатором эндоморфизмов, а не композицией, тогда $A\wedge A={\frac {1}{2}}[A,A]$, и в этих альтернативных обозначениях структурное уравнение Картана принимает форму

$F_{\nabla }=dA+{\frac {1}{2}}[A,A].$

Это альтернативное обозначение обычно используется в теории основных связностей расслоений, где вместо этого мы используем форму соединения $\omega$, -значная однозначная форма алгебры Ли , для которой нет понятия композиции (в отличие от случая эндоморфизмов), но есть понятие скобки Ли.

В некоторых источниках (см., например, ( MadsenTornehave1997 )) уравнение структуры Картана может быть записано со знаком минус:

$F_{\nabla }=dA-A\wedge A.$

В этом другом соглашении используется порядок умножения матриц, отличный от стандартной записи Эйнштейна в клиновом произведении матричных единых форм.

Личность Бьянки

Версия второго (дифференциального) тождества Бьянки из римановой геометрии справедлива для связности на любом векторном расслоении. Напомним, что связь $\nabla$ на векторном расслоении $E\to M$ индуцирует эндоморфизм-связность на $\operatorname {End} (E)$. Эта связность эндоморфизма сама по себе имеет внешнюю ковариантную производную, которую мы неоднозначно называем $d_{\nabla }$. Поскольку кривизна является глобально определенной $\operatorname {End} (E)$-значной двухформе, к ней можно применить внешнюю ковариантную производную. Личность Бьянки говорит, что

$d_{\nabla }F_{\nabla }=0$.

Это кратко отражает сложные тензорные формулы тождества Бьянки в случае римановых многообразий, и это уравнение можно перевести к стандартным тождествам Бьянки, расширив связность и кривизну в локальных координатах.

В целом не существует аналога первого ( алгебраического) тождества Бьянки для общей связности, поскольку оно использует специальные симметрии связности Леви-Чивита. А именно, можно использовать тот факт, что индексы векторных расслоений $E=TM$ в тензоре кривизны $R$ можно поменять местами с индексами котангенса расслоения, полученными из $T^{*}M$после использования метрики для понижения или повышения индексов. Например, это позволяет выполнить условие отсутствия кручения $\Gamma _{\ell i}^{\ \ j}=\Gamma _{i\ell }^{\ \ j}$ должно быть определено для связности Леви-Чивита, но для общего векторного расслоения $\ell$-index относится к локальной базе координат $T^{*}M$и $i,j$-индексы локальной системы координат $E$ и $E^{*}$ исходящий из разделения $\mathrm {End} (E)=E^{*}\otimes E$. Однако в особых обстоятельствах, например, когда ранг $E$ равен размерности $M$ и форма припоя выбрана, можно использовать пайку для замены индексов и определения понятия кручения для аффинных соединений, не являющихся связями Леви-Чивита.

Калибровочные преобразования

См. также: Группа датчиков (математика)

Учитывая две связи $\nabla _{1},\nabla _{2}$ на векторном расслоении $E\to M$, естественно задаться вопросом, когда их можно считать эквивалентными. Существует четко определенное понятие автоморфизма векторного расслоения. $E\to M$. Секция $u\in \Gamma (\operatorname {End} (E))$ является автоморфизмом, если $u(x)\in \operatorname {End} (E_{x})$ обратим в каждой точке $x\in M$. Такой автоморфизм называется преобразованием калибровочным $E$, а группа всех автоморфизмов называется калибровочной группой , часто обозначаемой ${\mathcal {G}}$ или $\operatorname {Aut} (E)$. Группу калибровочных преобразований можно четко охарактеризовать как пространство сечений присоединенного расслоения капитала. $\operatorname {Ad} ({\mathcal {F}}(E))$ векторного расслоения кадров расслоения $E$. Не следует путать это слово с строчной буквой. присоединенным расслоением, записанным $\operatorname {ad} ({\mathcal {F}}(E))$, что естественным образом отождествляется с $\operatorname {End} (E)$сам. Пакет $\operatorname {Ad} {\mathcal {F}}(E)$ является ассоциированным расслоением с расслоением главного фрейма с помощью представления сопряжения $G=\operatorname {GL} (r)$ на себе, $g\mapsto ghg^{-1}$, и имеет слой одной и той же общей линейной группы $\operatorname {GL} (r)$ где $\operatorname {rank} (E)=r$. Обратите внимание, что, несмотря на то же волокно, что и в пакете рамок, ${\mathcal {F}}(E)$ и будучи связанным с ним, $\operatorname {Ad} ({\mathcal {F}}(E))$не равен ни пакету фреймов, ни даже самому главному пакету. Калибровочную группу можно эквивалентно охарактеризовать как ${\mathcal {G}}=\Gamma (\operatorname {Ad} {\mathcal {F}}(E)).$

Калибровочное преобразование $u$ из $E$ действует на разделы $s\in \Gamma (E)$, и, следовательно, действует на соединения сопряжением. Явно, если $\nabla$ это соединение на $E$, то определяют $u\cdot \nabla$ к

$(u\cdot \nabla )_{X}(s)=u(\nabla _{X}(u^{-1}(s))$

для $s\in \Gamma (E),X\in \Gamma (TM)$. Чтобы проверить это $u\cdot \nabla$ это соединение, проверяется правило продукта

${\begin{aligned}u\cdot \nabla (fs)&=u(\nabla (u^{-1}(fs)))\\&=u(\nabla (fu^{-1}(s)))\\&=u(df\otimes u^{-1}(s))+u(f\nabla (u^{-1}(s)))\\&=df\otimes s+fu\cdot \nabla (s).\end{aligned}}$

Можно проверить, что это определяет левое групповое действие ${\mathcal {G}}$ на аффинном пространстве всех связностей ${\mathcal {A}}$.

С ${\mathcal {A}}$ представляет собой аффинное пространство, смоделированное по $\Omega ^{1}(M,\operatorname {End} (E))$, должна существовать некоторая эндоморфизмозначная одноформа $A_{u}\in \Omega ^{1}(M,\operatorname {End} (E))$ такой, что $u\cdot \nabla =\nabla +A_{u}$. Используя определение связи эндоморфизмов $\nabla ^{\operatorname {End} (E)}$ индуцированный $\nabla$, видно, что

$u\cdot \nabla =\nabla -d^{\nabla }(u)u^{-1}$

то есть $A_{u}=-d^{\nabla }(u)u^{-1}$.

Две связности называются калибровочно эквивалентными, если они различаются действием калибровочной группы и фактор-пространства ${\mathcal {B}}={\mathcal {A}}/{\mathcal {G}}$ — пространство модулей всех связностей на $E$. В общем, это топологическое пространство не является ни гладким многообразием, ни даже хаусдорфовым пространством , но содержит внутри себя пространство модулей связностей Янга–Миллса на $E$, что представляет значительный интерес в калибровочной теории и физике .

Примеры

• Классическая ковариантная производная или аффинная связность определяет связь на касательном расслоении к M или, в более общем плане, на любом тензорном расслоении , образованном путем взятия тензорных произведений касательного расслоения на себя и на двойственное ему расслоение.
• Соединение включено $\pi :\mathbb {R} ^{2}\times \mathbb {R} \to \mathbb {R}$ можно явно описать как оператор

$\nabla =d+{\begin{bmatrix}f_{11}(x)&f_{12}(x)\\f_{21}(x)&f_{22}(x)\end{bmatrix}}dx$

где $d$ - внешняя производная, вычисляемая на векторнозначных гладких функциях и $f_{ij}(x)$гладкие. Секция $a\in \Gamma (\pi )$ можно узнать по карте

${\begin{cases}\mathbb {R} \to \mathbb {R} ^{2}\\x\mapsto (a_{1}(x),a_{2}(x))\end{cases}}$

а потом

$\nabla (a)=\nabla {\begin{bmatrix}a_{1}(x)\\a_{2}(x)\end{bmatrix}}={\begin{bmatrix}{\frac {da_{1}(x)}{dx}}+f_{11}(x)a_{1}(x)+f_{12}(x)a_{2}(x)\\{\frac {da_{2}(x)}{dx}}+f_{21}(x)a_{1}(x)+f_{22}(x)a_{2}(x)\end{bmatrix}}dx$

• Если расслоение наделено метрикой расслоения , скалярным произведением на его слоях векторного пространства, метрическое соединение определяется как соединение, совместимое с метрикой расслоения.
• Связь Янга-Миллса — это специальная метрическая связь , удовлетворяющая Янга-Миллса . уравнениям движения
• Риманова связность — это метрическая связность на касательном расслоении риманова многообразия .
• Связность Леви-Чивита — это специальная риманова связность: метрически совместимая связность на касательном расслоении, которая также не имеет кручения . Оно уникально в том смысле, что для любой римановой связности всегда можно найти одну и только одну эквивалентную связность без кручения. «Эквивалент» означает, что он совместим с одной и той же метрикой, хотя тензоры кривизны могут быть разными; см. телепараллелизм . Разница между римановой связью и соответствующей связью Леви-Чивита определяется тензором искривления .
• Внешняя производная представляет собой плоскую связь на $E=M\times \mathbb {R}$ (тривиальное линейное расслоение над M ).
• В более общем смысле, существует каноническая плоская связность на любом плоском векторном расслоении (т. е. векторном расслоении, все функции перехода которого постоянны), которое задается внешней производной в любой тривиализации.

См. также

• D-модуль
• Связь (математика)

Ссылки

• Черн, Шиинг-Шен (1951), Темы дифференциальной геометрии , Институт перспективных исследований, конспекты лекций, отпечатанные на мимеографе.
• Дарлинг, RWR (1994), Дифференциальные формы и связи , Кембридж, Великобритания: Издательство Кембриджского университета, Бибкод : 1994dfc..book.....D , ISBN  0-521-46800-0
• Кобаяши, Шошичи; Номидзу, Кацуми (1996) [1963], Основы дифференциальной геометрии, Том. 1 , Библиотека классики Wiley, Нью-Йорк: Wiley Interscience , ISBN  0-471-15733-3
• Кошул, Дж. Л. (1950), «Гомологии и когомологии алгебр Ли», Бюллетень Математического общества , 78 : 65–127, doi : 10.24033/bsmf.1410
• Уэллс, Р.О. (1973), Дифференциальный анализ комплексных многообразий , Springer-Verlag, ISBN  0-387-90419-0
• Эмброуз, В.; Сингер, И.М. (1953), «Теорема о голономии», Труды Американского математического общества , 75 (3): 428–443, doi : 10.2307/1990721 , JSTOR   1990721

• Дональдсон С.К. и Кронхаймер П.Б., 1997. Геометрия четырехмногообразий. Издательство Оксфордского университета.

• Ту, Л.В., 2017. Дифференциальная геометрия: связности, кривизна и характеристические классы (т. 275). Спрингер.

• Таубес, CH, 2011. Дифференциальная геометрия: расслоения, связности, метрика и кривизна (том 23). ОУП Оксфорд.

• Ли, Дж. М., 2018. Введение в римановы многообразия. Международное издательство Спрингер.
• Мэдсен, Айдахо; Торнехейв, Дж. (1997), От исчисления к когомологиям: когомологии де Рама и характеристические классы , Cambridge University Press