Координаты Риндлера

Координаты Риндлера — это система координат, используемая в контексте специальной теории относительности для описания гиперболического ускорения равномерно ускоряющейся системы отсчета в плоском пространстве-времени. В релятивистской физике координаты гиперболически ускоренной системы отсчета. представляют собой важную и полезную карту координат, представляющую часть плоского пространства-времени Минковского . В специальной теории относительности равномерно ускоряющаяся частица испытывает гиперболическое движение , для чего можно выбрать равномерно ускоряющуюся систему отсчета , в которой она покоится в качестве собственной системы отсчета . Явления в этой гиперболически ускоренной системе отсчета можно сравнить с эффектами, возникающими в однородном гравитационном поле . Общий обзор ускорений в плоском пространстве-времени см. в разделах « Ускорение (специальная теория относительности)» и «Правильная система отсчета (плоское пространство-время)» .

В этой статье скорость света определяется как c = 1 , координаты инерциальные ( X , Y , Z , T ) , а гиперболические координаты ( x , y , z , t ) . Эти гиперболические координаты можно разделить на два основных варианта в зависимости от положения ускоренного наблюдателя: если наблюдатель находится в момент времени T = 0 в положении X = 1/α (где α является постоянным собственным ускорением, измеряемым сопутствующим акселерометром ), то гиперболические координаты часто называют координатами Риндлера с соответствующей метрикой Риндлера . Если наблюдатель находится в момент времени T = 0 в позиции X = 0 , то гиперболические координаты иногда называют координатами Мёллера. или координаты Коттлера–Мёллера с соответствующей метрикой Коттлера–Мёллера . Альтернативная карта, часто связанная с наблюдателями в гиперболическом движении, получается с использованием радиолокационных координат. которые иногда называют координатами Ласса . Как координаты Коттлера – Мёллера, так и координаты Ласса также обозначаются как координаты Риндлера.

Что касается истории, то такие координаты были введены вскоре после появления специальной теории относительности, когда они изучались (полностью или частично) наряду с концепцией гиперболического движения: По отношению к плоскому пространству-времени Минковского Альбертом Эйнштейном (1907, 1912), Макс Борн (1909), Арнольд Зоммерфельд (1910), Макс фон Лауэ (1911), Хендрик Лоренц (1913), Фридрих Коттлер (1914), Вольфганг Паули (1921), Карл Боллерт (1922), Степан Мохоровичич (1922), Жорж Леметр (1924), Эйнштейн и Натан Розен (1935), Кристиан Мёллер (1943, 1952), Фриц Рорлих (1963), Гарри Ласс (1963), и в отношении плоского и искривленного пространства-времени Вольфганга общей теории относительности Риндлера ( 1960, 1966). Подробности и источники см. в § История .

Характеристики системы Риндлера

Диаграмма Риндлера, для $\alpha =0.5$ в уравнении ( 1a ), построенном на диаграмме Минковского. Пунктирные линии — горизонты Риндлера.

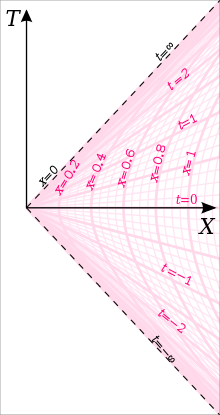
тела Мировая линия , находящегося в гиперболическом движении с постоянным собственным ускорением. $\alpha$ в $X$-направление как функция собственного времени $\tau$ и быстрота $\alpha \tau$ может быть предоставлено

$T=x\sinh(\alpha \tau ),\quad X=x\cosh(\alpha \tau )$

где $x=1/\alpha$ является постоянным и $\alpha \tau$ переменная, мировая линия напоминает гиперболу $X^{2}-T^{2}=x^{2}$. Летнее поле показал, что уравнения можно переинтерпретировать, определив $x$ как переменная и $\alpha \tau$ как постоянная, так что она представляет собой одновременную «форму покоя» тела, находящегося в гиперболическом движении, измеренную сопровождающим его наблюдателем. Используя собственное время наблюдателя как время всей гиперболически ускоренной системы отсчета, установив $\tau =t$, формулы преобразования между инерциальными координатами и гиперболическими координатами, следовательно, таковы:

$T=x\sinh(\alpha t),\quad X=x\cosh(\alpha t),\quad Y=y,\quad Z=z$ ( 1а )

с обратным

$t={\frac {1}{\alpha }}\operatorname {artanh} \left({\frac {T}{X}}\right),\quad x={\sqrt {X^{2}-T^{2}}},\quad y=Y,\quad z=Z$

Дифференцируем и вставляем в метрику Минковского.

$\mathrm {d} s^{2}=-\mathrm {d} T^{2}+\mathrm {d} X^{2}+\mathrm {d} Y^{2}+\mathrm {d} Z^{2},$

метрика вид в гиперболически ускоренной системе отсчета имеет

$\mathrm {d} s^{2}=-(\alpha x)^{2}\mathrm {d} t^{2}+\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}.$ ( 1б )

Эти преобразования определяют наблюдателя Риндлера как наблюдателя, который «покоится» в координатах Риндлера, т. е. поддерживает постоянные x , y , z и меняет только t с течением времени. Координаты действительны в регионе. $0<X<\infty ,\;-X<T<X$, который часто называют клином Риндлера , если $\alpha$ представляет собственное ускорение (вдоль гиперболы $x=1/\alpha$) наблюдателя Риндлера, собственное время которого определено равным координатному времени Риндлера. Чтобы поддерживать эту мировую линию, наблюдатель должен ускоряться с постоянным собственным ускорением, причем наблюдатели Риндлера находятся ближе к $x=0$ ( горизонт Риндлера ), имеющий большее собственное ускорение. Все наблюдатели Риндлера мгновенно покоятся в момент времени. $T=0$ в инерциальной системе отсчета, а в это время наблюдатель Риндлера с собственным ускорением $\alpha _{i}$ будет на позиции $X=1/\alpha _{i}$ (Действительно $X=c^{2}/\alpha _{i}$, но мы предполагаем единицы, где $c=1$), что также является постоянным расстоянием наблюдателя от горизонта Риндлера в координатах Риндлера. Если все наблюдатели Риндлера установят свои часы на ноль в $T=0$, то при определении системы координат Риндлера у нас есть выбор, какое собственное время наблюдателя Риндлера будет равно координатному времени $t$ в координатах Риндлера, и собственное ускорение этого наблюдателя определяет значение $\alpha$ выше (для других наблюдателей Риндлера на разных расстояниях от горизонта Риндлера координатное время будет равно некоторому постоянному кратному их собственному времени). Обычно систему координат Риндлера определяют так, чтобы наблюдатель Риндлера, собственное время которого совпадает с координатным временем, имел правильное ускорение. $\alpha =1$, так что $\alpha$ можно исключить из уравнений.

Приведенное выше уравнение было упрощено для $c=1$. Неупрощенное уравнение более удобно для нахождения расстояния до горизонта Риндлера, учитывая ускорение $\alpha$.

${\begin{aligned}&t={\frac {c}{\alpha }}\operatorname {artanh} \left({\frac {cT}{X}}\right)\;{\overset {X\,\gg \,cT}{\approx }}\;{\frac {c^{2}T}{\alpha X}}\\&\Rightarrow X\approx {\frac {c^{2}T}{\alpha t}}\;{\overset {T\,\approx \,t}{\approx }}\;{\frac {c^{2}}{\alpha }}\end{aligned}}$

Оставшаяся часть статьи будет следовать соглашению об установке обоих $\alpha =1$ и $c=1$, поэтому единицы для $X$ и $x$ будет 1 единица $=c^{2}/\alpha =1$. Помните, что настройка $\alpha =1$ световая секунда/секунда ² сильно отличается от настройки $\alpha =1$ световой год/год ² . Даже если мы выберем единицы, где $c=1$, величина собственного ускорения $\alpha$ будет зависеть от нашего выбора единиц измерения: например, если мы используем единицы светового года для измерения расстояния ( $X$ или $x$) и годы для времени, ( $T$ или $t$), это будет означать $\alpha =1$ световой год/год ² , равная примерно 9,5 метра в секунду ² , а если для измерения расстояния использовать единицы световых секунд, ( $X$ или $x$) и секунды для времени ( $T$ или $t$), это будет означать $\alpha =1$ световая секунда/секунда ² , или 299 792 458 метров в секунду ² ).

Варианты формул преобразования

Приведен более общий вывод формул преобразования, когда соответствующая тетрада Ферми – Уокера формулируется координаты Ферми или собственные координаты . , из которой могут быть получены В зависимости от выбора начала координат этих координат можно вывести метрику - замедление времени между временем в начале координат. $dt_{0}$ и $dt$ в точку $x$, а координата скорости света $|dx|/|dt|$ (эта переменная скорость света не противоречит специальной теории относительности, поскольку является лишь артефактом используемых ускоренных координат, тогда как в инерциальных координатах она остается постоянной). Вместо координат Ферми могут использоваться также Радарные координаты, которые получаются путем определения расстояния с помощью световых сигналов (см. раздел Понятия о расстоянии ), благодаря чему метрика, замедление времени и скорость света больше не зависят от координат – в частности , координатная скорость света остается такой же, как и скорость света. $(c=1)$ в инерциальных системах отсчета:

$X$ в $T=0$	Преобразование, метрика, замедление времени и координатная скорость света.
$X=0$	Координаты Коттлера – Мёллера
	${\begin{array}{c|c}{\begin{aligned}T&=\left(x+{\frac {1}{\alpha }}\right)\sinh(\alpha t)\\X&=\left(x+{\frac {1}{\alpha }}\right)\cosh(\alpha t)-{\frac {1}{\alpha }}\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} \left({\frac {T}{X+{\frac {1}{\alpha }}}}\right)\\x&={\sqrt {\left(X+{\frac {1}{\alpha }}\right)^{2}-T^{2}}}-{\frac {1}{\alpha }}\\y&=Y\\z&=Z\end{aligned}}\end{array}}$ ( 2а ) $ds^{2}=-(1+\alpha x){}^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}$ ( 2б ) $dt=(1+\alpha x)dt_{0},\qquad {\frac {|dx|}{|dt|}}=1+\alpha x$ ( 2с )
	Координаты Риндлера
$X={\frac {1}{\alpha }}$	${\begin{array}{c|c}{\begin{aligned}T&=x\sinh(\alpha t)\\X&=x\cosh(\alpha t)\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} {\frac {T}{X}}\\x&={\sqrt {X^{2}-T^{2}}}\\y&=Y\\z&=Z\end{aligned}}\end{array}}$ ( 2д ) $ds^{2}=-(\alpha x)^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}$ ( 2е ) $dt=\alpha x\ dt_{0},\qquad {\frac {|dx|}{|dt|}}=\alpha x$ ( 2ф )
	Радарные координаты (координаты Ласса)
$X={\frac {1}{\alpha }}$	${\begin{array}{c|c}{\begin{aligned}T&={\frac {1}{\alpha }}e^{\alpha x}\sinh(\alpha t)\\X&={\frac {1}{\alpha }}e^{\alpha x}\cosh(\alpha t)\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} {\frac {T}{X}}\\x&={\frac {1}{2\alpha }}\ln \left[\alpha {}^{2}\left(X^{2}-T^{2}\right)\right]\\y&=Y\\z&=Z\end{aligned}}\end{array}}$ ( 2г )
	$ds^{2}=e^{2\alpha x}\left(-dt^{2}+dx^{2}\right)+dy^{2}+dz^{2}$ ( 2 часа ) $dt=e^{\alpha x}dt_{0},\qquad {\frac {|dx|}{|dt|}}=1$ ( 2и )

Наблюдатели Риндлера

На новой диаграмме ( 1а ) с $c=1$ и $\alpha =1$, естественно взять поле кофрейма

$d\sigma ^{0}=x\,dt,\;\;d\sigma ^{1}=dx,\;\;d\sigma ^{2}=dy,\;\;d\sigma ^{3}=dz$

который имеет двойное поле кадра

${\vec {e}}_{0}={\frac {1}{x}}\partial _{t},\;\;{\vec {e}}_{1}=\partial _{x},\;\;{\vec {e}}_{2}=\partial _{y},\;\;{\vec {e}}_{3}=\partial _{z}$

Это определяет локальную систему Лоренца в касательном пространстве в каждом событии (в области, охватываемой нашей диаграммой Риндлера, а именно в клине Риндлера). Интегральные кривые времениподобного поля единичного векторного ${\vec {e}}_{0}$ дают времениподобное сравнение , состоящее из мировых линий семейства наблюдателей, называемых наблюдателями Риндлера . На диаграмме Риндлера эти мировые линии отображаются как вертикальные координатные линии. $x=x_{0},\;y=y_{0},\;z=z_{0}$. Используя приведенное выше преобразование координат, мы обнаруживаем, что они соответствуют гиперболическим дугам в исходной декартовой карте.

Некоторые типичные наблюдатели Риндлера (темно-синие гиперболические дуги) изображены с использованием декартовой карты. Красные линии под углом 45 градусов от вертикали представляют горизонт Риндлера; система координат Риндлера определена только справа от этой границы.

Как и любое времяподобное сравнение в любом лоренцевом многообразии, это сравнение имеет кинематическое разложение (см. уравнение Райчаудхури ). В этом случае расширение и завихренность конгруэнции наблюдателей Риндлера исчезают . Исчезновение тензора расширения означает, что каждый из наших наблюдателей сохраняет постоянное расстояние до своих соседей . Исчезновение тензора завихренности означает, что мировые линии наших наблюдателей не закручиваются друг вокруг друга; это своего рода локальное отсутствие «закрутки».

Вектор ускорения каждого наблюдателя задается ковариантной производной

$\nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}={\frac {1}{x}}{\vec {e}}_{1}$

То есть каждый наблюдатель Риндлера ускоряется в $\partial _{x}$ направление. Говоря индивидуально, каждый наблюдатель фактически ускоряется с постоянной величиной в этом направлении, поэтому их мировые линии являются лоренцевыми аналогами окружностей, которые являются кривыми постоянной кривизны пути в евклидовой геометрии.

Поскольку наблюдатели Риндлера не имеют завихренности , они также ортогональны гиперповерхности . Ортогональные пространственные гиперсрезы $t=t_{0}$; они выглядят как горизонтальные полуплоскости на диаграмме Риндлера и как полуплоскости, проходящие через $T=X=0$ в декартовой карте (см. рисунок выше). Параметр $dt=0$ в линейном элементе мы видим, что они имеют обычную евклидову геометрию, $d\sigma ^{2}=dx^{2}+dy^{2}+dz^{2},\;\forall x>0,\forall y,z$. Таким образом, пространственные координаты на карте Риндлера имеют очень простую интерпретацию, согласующуюся с утверждением о взаимной стационарности наблюдателей Риндлера. Мы вернемся к этому свойству жесткости наблюдателей Риндлера чуть позже в этой статье.

«Парадоксальное» свойство

Обратите внимание, что наблюдателям Риндлера с меньшей постоянной координатой x сложнее успевать за ускорением. Это может показаться удивительным, поскольку в ньютоновской физике наблюдатели, сохраняющие постоянное относительное расстояние, должны иметь одинаковое ускорение. Но в релятивистской физике мы видим, что задний конец стержня, который ускоряется какой-то внешней силой (параллельной его оси симметрии), должен ускоряться немного сильнее, чем ведущий конец, иначе он должен в конечном итоге сломаться. Это проявление лоренцева сокращения . По мере ускорения стержня его скорость увеличивается, а длина уменьшается. Поскольку он становится короче, задняя часть должна ускоряться сильнее, чем передняя. Другой взгляд на это таков: серверная часть должна достичь такого же изменения скорости за более короткий период времени. Это приводит к дифференциальному уравнению, показывающему, что на некотором расстоянии ускорение заднего конца расходится, в результате чего образуется горизонт Риндлера .

Это явление лежит в основе хорошо известного «парадокса» — парадокса космического корабля Белла . Однако это простое следствие релятивистской кинематики. Один из способов убедиться в этом — заметить, что величина вектора ускорения — это всего лишь кривизна траектории соответствующей мировой линии. Но мировые линии наших наблюдателей Риндлера являются аналогами семейства концентрических окружностей в евклидовой плоскости, поэтому мы просто имеем дело с лоренцевым аналогом факта, знакомого конькобежцам: в семействе концентрических окружностей внутренние окружности должны изгибаться быстрее (на единицу длины дуги), чем внешние .

Наблюдатели Минковского

Репрезентативный наблюдатель Минковского (темно-синяя гиперболическая секущая кривая), изображенный с использованием диаграммы Риндлера. Горизонт Риндлера показан красным.

Целесообразно также ввести альтернативную систему координат, заданную в таблице Минковского естественным выбором.

${\vec {f}}_{0}=\partial _{T},\;{\vec {f}}_{1}=\partial _{X},\;{\vec {f}}_{2}=\partial _{Y},\;{\vec {f}}_{3}=\partial _{Z}$

Преобразовав эти векторные поля с помощью приведенного выше преобразования координат, мы обнаружим, что в карте Риндлера (в клине Риндера) эта система координат принимает вид

${\begin{aligned}{\vec {f}}_{0}&={\frac {1}{x}}\cosh(t)\,\partial _{t}-\sinh(t)\,\partial _{x}\\{\vec {f}}_{1}&=-{\frac {1}{x}}\sinh(t)\,\partial _{t}+\cosh(t)\,\partial _{x}\\{\vec {f}}_{2}&=\partial _{y},\;{\vec {f}}_{3}=\partial _{z}\end{aligned}}$

Вычисление кинематического разложения времениподобного сравнения, определяемого временемподобным полем единичного вектора ${\vec {f}}_{0}$, мы обнаруживаем, что расширение и завихренность снова исчезают, а кроме того, исчезает и вектор ускорения: $\nabla _{{\vec {f}}_{0}}{\vec {f}}_{0}=0$. Другими словами, это геодезическое соответствие ; соответствующие наблюдатели находятся в состоянии инерционного движения . В исходной декартовой карте эти наблюдатели, которых мы будем называть наблюдателями Минковского , находятся в состоянии покоя.

На карте Риндлера мировые линии наблюдателей Минковского выглядят как гиперболические секущие кривые, асимптотические относительно координатной плоскости. $x=0$. В частности, в координатах Риндлера мировая линия наблюдателя Минковского, проходящая через событие $t=t_{0},\;x=x_{0},\;y=y_{0},\;z=z_{0}$ является

${\begin{aligned}t&=\operatorname {artanh} \left({\frac {s}{x_{0}}}\right),\;-x_{0}<s<x_{0}\\x&={\sqrt {x_{0}^{2}-s^{2}}},\;-x_{0}<s<x_{0}\\y&=y_{0}\\z&=z_{0}\end{aligned}}$

где $s$ это собственное время этого наблюдателя Минковского. Обратите внимание, что карта Риндлера охватывает лишь небольшую часть его истории. Это ясно показывает, почему карта Риндлера не является геодезически полной ; времениподобные геодезические проходят за пределами области, покрытой картой, за конечное собственное время. Конечно, мы уже знали, что карта Риндлера не может быть геодезически полной, поскольку она охватывает лишь часть исходной декартовой карты, которая является геодезически полной картой.

В случае, изображенном на рисунке, $x_{0}=1$ и мы нарисовали (правильно масштабировали и увеличили) световые конусы на $s\in \left\{-{\frac {1}{2}},\;0,\;{\frac {1}{2}}\right\}$.

Горизонт

Координатная карта Риндлера имеет координатную особенность в точке x = 0, где метрический тензор (выраженный в координатах Риндлера) имеет исчезающий определитель . Это происходит потому, что при x → 0 ускорение наблюдателей Риндлера расходится. Как видно из рисунка, иллюстрирующего клин Риндлера, локус x = 0 в диаграмме Риндлера соответствует локусу T ² = Х ² , X > 0 в декартовой карте, которая состоит из двух нулевых полуплоскостей, каждая из которых управляется нулевой геодезической конгруэнцией.

На данный момент мы просто рассматриваем горизонт Риндлера как границу координат Риндлера. Если рассматривать совокупность ускоряющихся наблюдателей, имеющих постоянное положение в координатах Риндлера, то ни один из них никогда не сможет получить световые сигналы от событий с T ≥ X или слева от нее (на диаграмме это будут события на линии T = ). X , вдоль которого лежит верхний красный горизонт; однако эти наблюдатели могли бы получать сигналы от событий с T ≥ X , если бы они прекратили ускорение и сами пересекли эту линию), и они никогда не могли бы посылать сигналы событиям с T ≤ − X (события на или левее линии T = − X , вдоль которой лежит нижний красный горизонт, эти события лежат вне всех будущих световых конусов своей прошлой мировой линии); Кроме того, если мы рассмотрим членов этого набора ускоряющихся наблюдателей все ближе и ближе к горизонту, в пределе, когда расстояние до горизонта приближается к нулю, постоянное собственное ускорение, испытываемое наблюдателем на этом расстоянии (которое также будет G- сила, испытываемая таким наблюдателем) приближалась бы к бесконечности. Оба эти факта также были бы верны, если бы мы рассматривали группу наблюдателей, парящих за пределами Горизонт событий черной дыры , где каждый наблюдатель зависает на постоянном радиусе в координатах Шварцшильда . Фактически, в непосредственной близости от черной дыры геометрия, близкая к горизонту событий, может быть описана в координатах Риндлера. Излучение Хокинга в случае ускоряющейся системы отсчета называется излучением Унру . Связь представляет собой эквивалентность ускорения гравитации.

Геодезика

Уравнения геодезических на карте Риндлера легко получаются из геодезического лагранжиана ; они есть

${\ddot {t}}+{\frac {2}{x}}\,{\dot {x}}\,{\dot {t}}=0,\;{\ddot {x}}+x\,{\dot {t}}^{2}=0,\;{\ddot {y}}=0,\;{\ddot {z}}=0$

Конечно, в исходной декартовой карте геодезические линии выглядят как прямые линии, поэтому мы могли бы легко получить их на карте Риндлера, используя наше преобразование координат. Однако полезно получить и изучить их независимо от исходной карты, и мы сделаем это в этом разделе.

Некоторые репрезентативные нулевые геодезические (черные гиперболические полукруги), проецируемые в пространственный гиперсрез t = 0 наблюдателей Риндлера. Горизонт Риндлера показан пурпурной плоскостью.

Из первого, третьего и четвертого сразу получаем первые интегралы

${\dot {t}}={\frac {E}{x^{2}}},\;\;{\dot {y}}=P,\;\;{\dot {z}}=Q$

Но из линейного элемента мы имеем $\varepsilon =-x^{2}\,{\dot {t}}^{2}+{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}$ где $\varepsilon \in \left\{-1,\,0,\,1\right\}$ для времениподобных, нулевых и пространственноподобных геодезических соответственно. Это дает четвертый первый интеграл, а именно

${\dot {x}}^{2}=\left(\varepsilon +{\frac {E^{2}}{x^{2}}}\right)-P^{2}-Q^{2}$.

Этого достаточно, чтобы дать полное решение уравнений геодезических.

В случае нулевых геодезических из ${\frac {E^{2}}{x^{2}}}\,-\,P^{2}\,-\,Q^{2}$ с ненулевым $E$, мы видим, что координата x изменяется в интервале

$0\,<\,x\,<\,{\frac {E}{\sqrt {P^{2}\,+\,Q^{2}}}}$.

Полное семейство из семи параметров, дающее любую нулевую геодезическую через любое событие в клине Риндлера, равно

${\begin{aligned}t-t_{0}&=\operatorname {artanh} \left({\frac {1}{E}}\left[s\left(P^{2}+Q^{2}\right)-{\sqrt {E^{2}-\left(P^{2}+Q^{2}\right)x_{0}^{2}}}\right]\right)+\\&\qquad \operatorname {artanh} \left({\frac {1}{E}}{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}\right)\\x&={\sqrt {x_{0}^{2}+2s{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}-s^{2}(P^{2}+Q^{2})}}\\y-y_{0}&=Ps;\;\;z-z_{0}=Qs\end{aligned}}$

Построение траекторий некоторых репрезентативных нулевых геодезических через данное событие (то есть проецирование на гиперсрез $t=0$), получаем картину, подозрительно похожую на совокупность всех полукругов, проходящих через точку и ортогональных горизонту Риндлера (см. рисунок).

Метрика Ферма

Тот факт, что в карте Риндлера проекции нулевых геодезических на любой пространственный гиперсрез для наблюдателей Риндлера представляют собой просто полукруглые дуги, можно проверить непосредственно из только что данного общего решения, но есть очень простой способ убедиться в этом. Статическое пространство-время свободное от завихренности времяподобное векторное поле Киллинга — это пространство, в котором можно найти . В этом случае мы имеем однозначно определенное семейство (идентичных) пространственных гиперсрезов, ортогональных соответствующим статическим наблюдателям (которые не обязательно должны быть инерционными наблюдателями). Это позволяет нам определить новую метрику на любом из этих гиперсрезов, которая конформно связана с исходной метрикой, унаследованной от пространства-времени, но со свойством, что геодезические в новой метрике (обратите внимание, что это риманова метрика на римановом трехмерном многообразии) являются в точности проекциями нулевых геодезических пространства-времени. Эта новая метрика называется метрикой Ферма , и в статическом пространстве-времени наделена координатной картой, в которой линейный элемент имеет вид

$ds^{2}=g_{00}\,dt^{2}+g_{jk}\,dx^{j}\,dx^{k},\;\;j,\;k\in \{1,2,3\}$

метрика Ферма на $t=0$ это просто

$d\rho ^{2}={\frac {1}{-g_{00}}}\left(g_{jk}\,dx^{j}\,dx^{k}\right)$

(где под метрическими коэффициентами понимаются значения, $t=0$).

В диаграмме Риндлера времяподобный перевод $\partial _{t}$ — такое векторное поле Киллинга, поэтому это статическое пространство-время (неудивительно, поскольку пространство-время Минковского, конечно, тривиально является статическим вакуумным решением уравнения поля Эйнштейна ). Поэтому мы можем сразу записать метрику Ферма для наблюдателей Риндлера:

$d\rho ^{2}={\frac {1}{x^{2}}}\left(dx^{2}+dy^{2}+dz^{2}\right),\;\;\forall x>0,\;\;\forall y,z$

Но это хорошо известный линейный элемент гиперболического трехмерного пространства H ³ в верхнем полупространстве диаграммы . Это очень похоже на хорошо известную диаграмму верхней полуплоскости гиперболической плоскости H. ² , которая знакома поколениям изучающих комплексный анализ в связи с задачами конформного отображения (и многим другим), и многие читатели с математическим складом ума уже знают, что геодезические H ² в модели верхней полуплоскости это просто полукруги (ортогональные окружности на бесконечности, представленной действительной осью).

Симметрии

Поскольку карта Риндлера является координатной картой пространства-времени Минковского, мы ожидаем найти десять линейно независимых векторных полей Киллинга. Действительно, в декартовой диаграмме мы можем легко найти десять линейно независимых векторных полей Киллинга, генерирующих соответственно однопараметрические подгруппы перевода времени , три пространственных пространства, три вращения и три повышения. Вместе они порождают (собственно изохронную) группу Пуанкаре, группу симметрии пространства-времени Минковского.

Однако поучительно записать и решить векторные уравнения Киллинга непосредственно. Мы получаем четыре знакомых векторных поля Киллинга.

$\partial _{t},\;\;\partial _{y},\;\;\partial _{z},\;\;-z\,\partial _{y}+y\,\partial _{z}$

(перенос во времени, пространственный сдвиг, ортогональный направлению ускорения, и пространственное вращение, ортогональное направлению ускорения) плюс еще шесть:

${\begin{aligned}&\exp(\pm t)\,\left({\frac {y}{x}}\,\partial _{t}\pm \left[y\,\partial _{x}-x\,\partial _{y}\right]\right)\\&\exp(\pm t)\,\left({\frac {z}{x}}\,\partial _{t}\pm \left[z\,\partial _{x}-x\,\partial _{z}\right]\right)\\&\exp(\pm t)\,\left({\frac {1}{x}}\,\partial _{t}\pm \partial _{x}\right)\end{aligned}}$

(где знаки выбраны последовательно + или -). Мы оставим это в качестве упражнения, чтобы выяснить, как они связаны со стандартными генераторами; здесь мы хотим отметить, что мы должны быть в состоянии получить генераторы, эквивалентные $\partial _{T}$ в декартовой карте, однако клин Риндлера явно не инвариантен при таком переносе. Как такое может быть? Ответ заключается в том, что, как и все, что определяется системой уравнений в частных производных на гладком многообразии, уравнение Киллинга, как правило, будет иметь локально определенные решения, но они могут не существовать глобально. То есть при соответствующих ограничениях на групповой параметр поток Киллинга всегда можно определить в подходящей локальной окрестности , но поток не может быть четко определен глобально . Это не имеет ничего общего с лоренцевыми многообразиями как таковыми, поскольку тот же вопрос возникает при изучении общих гладких многообразий .

Понятия расстояния

Один из многих ценных уроков, которые можно извлечь из изучения карты Риндлера, заключается в том, что на самом деле существует несколько различных (но разумных) понятий расстояния , которые могут использовать наблюдатели Риндлера.

Операционное значение радиолокационного расстояния между двумя наблюдателями Риндлера (темно-синие вертикальные линии). Горизонт Риндлера показан слева (красная вертикальная линия). Также изображена мировая линия радиолокационного импульса вместе со световыми конусами (правильно масштабированными) в событиях A, B, C.

Первый из них мы молчаливо использовали выше: индуцированная риманова метрика на пространственных гиперсрезах. $t=t_{0}$. Мы назовем это расстоянием линейки, поскольку оно соответствует этой индуцированной римановой метрике, но его рабочий смысл может быть не сразу очевиден.

С точки зрения физических измерений более естественным понятием расстояния между двумя мировыми линиями является радиолокационное расстояние . Это вычисляется путем отправки нулевой геодезической линии от мировой линии нашего наблюдателя (событие A) к мировой линии некоторого небольшого объекта, после чего она отражается (событие B) и возвращается к наблюдателю (событие C). Радиолокационное расстояние затем получается путем деления времени прохождения туда и обратно, измеренного идеальными часами, которые носит наш наблюдатель.

(К счастью, в пространстве-времени Минковского мы можем игнорировать возможность существования множественных нулевых геодезических путей между двумя мировыми линиями, но в космологических моделях и других приложениях все не так просто. Нам также следует предостеречь от предположения, что это понятие расстояния между двумя наблюдателями дает понятие, которое является симметричным при перестановке наблюдателей.)

В частности, рассмотрим пару наблюдателей Риндлера с координатами $x=x_{0},\;y=0,\;z=0$ и $x=x_{0}+h,\;y=0,\;z=0$ соответственно. (Обратите внимание, что первый из них, ведомый наблюдатель, ускоряется немного сильнее, чтобы не отставать от ведущего наблюдателя). Параметр $dy=dz=0$ в элементе линии Риндлера легко получаем уравнение нулевых геодезических, движущихся в направлении ускорения:

$t-t_{0}=\log \left({\frac {x}{x_{0}}}\right)$

Следовательно, радиолокационное расстояние между этими двумя наблюдателями определяется выражением

$x_{0}\,\log \left(1+{\frac {h}{x_{0}}}\right)=h-{\frac {h^{2}}{2\,x_{0}}}+O\left(h^{3}\right)$

Это немного меньше расстояния линейки, но для наблюдателей, находящихся рядом, расхождение незначительно.

Третье возможное понятие расстояния таково: наш наблюдатель измеряет угол , образованный единичным диском, помещенным на какой-то объект (не точечный объект), каким он кажется из его местоположения. Мы называем это расстоянием оптического диаметра . Благодаря простому характеру нулевых геодезических в пространстве-времени Минковского мы можем легко определить оптическое расстояние между нашей парой наблюдателей Риндлера (выровненных по направлению ускорения). Из эскиза должно быть правдоподобно, что расстояние оптического диаметра масштабируется как ${\textstyle h+{\frac {1}{x_{0}}}+O\left(h^{3}\right)}$. Следовательно, в случае, когда следящий наблюдатель оценивает расстояние до ведущего наблюдателя (случай $h>0$), оптическое расстояние немного больше расстояния линейки, которое немного больше расстояния радара. Теперь читателю следует рассмотреть случай, когда ведущий наблюдатель оценивает расстояние до идущего за ним наблюдателя.

Существуют и другие понятия расстояния, но главное ясно: хотя значения этих различных понятий в целом не совпадают для данной пары наблюдателей Риндлера, все они согласны с тем, что каждая пара наблюдателей Риндлера поддерживает постоянное расстояние . Тот факт, что очень близкие наблюдатели Риндлера взаимно стационарны, следует из отмеченного выше факта, что тензор разложения сравнения Риндлера тождественно обращается в нуль. Однако здесь мы показали, что в различных смыслах это свойство жесткости сохраняется и в более крупных масштабах. Это действительно замечательное свойство жесткости, учитывая хорошо известный факт, что в релятивистской физике ни один стержень не может быть жестко ускорен (и ни один диск не может жестко раскручиваться ) — по крайней мере, без воздействия неоднородных напряжений. Самый простой способ убедиться в этом — заметить, что в ньютоновской физике, если мы «пнем» твердое тело, все элементы материи в теле немедленно изменят свое состояние движения. Это, конечно, несовместимо с релятивистским принципом, согласно которому никакая информация, имеющая какой-либо физический эффект, не может передаваться со скоростью, превышающей скорость света.

Из этого следует, что если стержень ускоряется какой-то внешней силой, приложенной где-либо по его длине, элементы материи в различных местах стержня не могут все чувствовать одинаковую величину ускорения, если стержень не должен расширяться без ограничений и в конечном итоге сломаться. Другими словами, ускоренный стержень, который не ломается, должен выдерживать напряжения, изменяющиеся по его длине. Более того, в любом мысленном эксперименте с изменяющимися во времени силами, «пинаем» ли мы объект или пытаемся постепенно его ускорить, мы не можем избежать проблемы избежания механических моделей, несовместимых с релятивистской кинематикой (поскольку удаленные части тела реагируют слишком быстро к приложенной силе).

Возвращаясь к вопросу об эксплуатационном значении расстояния линейки, мы видим, что это должно быть то расстояние, которое получат наши наблюдатели, если очень медленно передадут из рук в руки небольшую линейку, неоднократно поставленную впритык. Но для детального обоснования этой интерпретации потребуется какая-то материальная модель.

Обобщение на искривленное пространство-время

Координаты Риндлера, описанные выше, могут быть обобщены на искривленное пространство-время как нормальные координаты Ферми . Суть обобщения заключается в построении соответствующей ортонормированной тетрады и последующей ее транспортировке по заданной траектории с использованием правила переноса Ферми-Уокера . Подробности см. в статье Ни и Циммермана в ссылках ниже. Такое обобщение фактически позволяет изучать инерционные и гравитационные эффекты в наземной лаборатории, а также более интересные связанные инерционно-гравитационные эффекты.

История

Обзор

Координаты Коттлера-Мёллера и Риндлера

Альберт Эйнштейн (1907) изучил эффекты в равномерно ускоренной системе отсчета, получив уравнения для координатно-зависимого замедления времени и скорости света, эквивалентные ( 2c ), и чтобы сделать формулы независимыми от начала координат наблюдателя, он получил замедление времени ( 2i ) в формальном согласии с Координаты радара. Вводя понятие жесткости Борна , Макс Борн (1909) отметил, что формулы гиперболического движения можно использовать в качестве преобразований в «гиперболически ускоренную систему отсчета» ( нем . Hyperbolisch beschleunigtes Bezugsystem ), эквивалентную ( 2d ). Работа Борна была развита Арнольдом Зоммерфельдом (1910). и Макс фон Лауэ (1911) оба получили ( 2d ), используя мнимые числа, которые были резюмированы Вольфгангом Паули (1921) который помимо координат ( 2d ) получил еще и метрику ( 2e ), используя мнимые числа. Эйнштейн (1912) изучил статическое гравитационное поле и получил метрику Коттлера-Мёллера ( 2b ), а также аппроксимации формул ( 2a ), используя координатно-зависимую скорость света. Хендрик Лоренц (1913) получил координаты, подобные ( 2d , 2e , 2f Эйнштейна ), при изучении принципа эквивалентности и однородного гравитационного поля.

Подробное описание дал Фридрих Коттлер (1914). который сформулировал соответствующую ортонормированную тетраду , формулы преобразования и метрику ( 2а , 2б ). Также Карл Боллерт (1922) получил метрику ( 2b ) в своем исследовании однородного ускорения и однородных гравитационных полей. В статье, посвященной жесткости Борна, Жорж Леметр (1924) полученные координаты и метрика ( 2a , 2b ). Альберт Эйнштейн и Натан Розен (1935) описали ( 2d , 2e ) как «хорошо известные» выражения для однородного гравитационного поля. По мотивам Кристиана Моллера (1943) полученные ( 2a , 2b ) в качестве исследования, связанного с однородными гравитационными полями, он (1952) а также Миснер, Торн и Уиллер (1973). использовал транспорт Ферми – Уокера, чтобы получить те же уравнения.

Хотя эти исследования касались плоского пространства-времени, Вольфганг Риндлер (1960) проанализировал гиперболическое движение в искривленном пространстве-времени и показал (1966) аналогия между гиперболическими координатами ( 2d , 2e ) в плоском пространстве-времени с координатами Краскала в пространстве Шварцшильда . Это повлияло на последующих авторов в их формулировке излучения Унру, измеряемого наблюдателем в гиперболическом движении, что аналогично описанию излучения Хокинга черных дыр .

Горизонт

Борн (1909) показал, что внутренние точки борновского твердого тела, находящегося в гиперболическом движении, могут находиться только в области $X/\left(X^{2}-T^{2}\right)>0$. Зоммерфельд (1910) определил, что координаты, допускающие преобразование между инерциальными и гиперболическими координатами, должны удовлетворять $T<X$. Коттлер (1914) определил этот регион как $X^{2}-T^{2}>0$, и указал на существование «пограничного самолета» ( нем . Grenzebene ) $c^{2}/\alpha +x$, за пределами которого никакой сигнал не может достичь наблюдателя при гиперболическом движении. назвал это «горизонтом наблюдателя» ( нем . Horizont des Beobachters ). Боллерт (1922) Риндлер (1966) продемонстрировал связь между таким горизонтом и горизонтом в координатах Краскала.

Координаты радара

Используя формализм Боллерта, Степан Мохоровичич (1922) сделал другой выбор для некоторого параметра и получил метрику ( 2h ) с ошибкой печати, которая была исправлена ​​Боллертом (1922b) с другой ошибкой печати, пока Мохоровичич (1923) не предоставил версию без ошибки печати. Вдобавок Мохоровичич ошибочно утверждал, что метрика ( 2b , теперь называемая метрикой Коттлера-Мёллера) неверна, что было опровергнуто Боллертом (1922). Метрика ( 2 часа ) была заново открыта Гарри Лассом (1963). который также дал соответствующие координаты ( 2g ), которые иногда называют «координатами Ласса». Метрика ( 2h ), как и ( 2a , 2b ), также была выведена Фрицем Рорлихом (1963). В конце концов, координаты Ласса ( 2g , 2h ) были отождествлены с координатами радара Desloge & Philpott (1987).

Таблица с историческими формулами

Эйнштейн (1907) ${\scriptstyle {\begin{matrix}\sigma =\tau \left(1+{\frac {\gamma \xi }{c^{2}}}\right)\\\sigma =\tau e^{\gamma \xi /c^{2}}\\c\left(1+{\frac {\gamma \xi }{c^{2}}}\right)\end{matrix}}}$ Родился (1909 г.) ${\scriptstyle {\begin{matrix}x=-q\xi ,\ y=\eta ,\ z=\zeta ,\ t={\frac {p}{c^{2}}}\xi \\\left(p=x_{\tau },\ q=-t_{\tau }={\sqrt {1+p^{2}/c^{2}}}\right)\\{\boldsymbol {\downarrow }}\\x^{2}-c^{2}t^{2}=\xi ^{2}\end{matrix}}}$ Херглотц (1909) ${\scriptstyle {\begin{matrix}{\begin{aligned}x&=x'\\y&=y'\\t-z&=(t'-z')e^{\vartheta }\\t+z&=(t'+z')e^{-\vartheta }\end{aligned}}\\{\boldsymbol {\downarrow }}\\x=x_{0},\quad y=y_{0},\quad z={\sqrt {z_{0}^{2}+t^{2}}}\end{matrix}}}$ Летнее поле (1910) $\scriptstyle {\begin{aligned}x&=r\cos \varphi \\y&=y'\\z&=z'\\l&=r\sin \varphi \\\varphi &=i\psi ,\ l=ict\end{aligned}}$ Лауэ (1911) $\scriptstyle {\begin{aligned}X&=R\cos \varphi \\L&=R\sin \varphi \\R^{2}&=X^{2}+L^{2}\\\tan \varphi &={\frac {L}{X}}\end{aligned}}$ Эйнштейн (1912) ${\scriptstyle {\begin{matrix}d\xi ^{2}-d\tau ^{2}=dx^{2}-c^{2}dt^{2}\\{\boldsymbol {\downarrow }}\\c=c_{0}+ax\\{\boldsymbol {\downarrow }}\\{\begin{aligned}\xi &=x+{\frac {ac}{2}}t^{2}\\\eta &=y\\\zeta &=z\\\tau &=ct\end{aligned}}\end{matrix}}}$ Коттлер (1912) ${\scriptstyle {\begin{aligned}x^{(1)}&=x_{0}^{(1)}\\x^{(2)}&=x_{0}^{(2)}\\x^{(3)}&=b\cos i\varphi \\x^{(4)}&=b\sin i\varphi \end{aligned}}}$ Лоренц (1913) ${\scriptstyle {\begin{matrix}dc={\frac {g}{c}}dz\\\hline {\begin{aligned}z&=a\left(z'-z_{0}^{\prime }\right)\\ct&=b\left(z'-z_{0}^{\prime }\right)\\a&={\frac {1}{2}}\left(e^{kt'}+e^{-kt}\right)\\b&={\frac {1}{2}}\left(e^{kt'}-e^{-kt}\right)\end{aligned}}\\{\boldsymbol {\downarrow }}\\c'=k\left(z'-z_{0}^{\prime }\right),\ z'-z_{0}^{\prime }={\frac {c^{2}}{g}}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}&dx^{2}+dy^{2}+dz^{2}-c^{2}dt\\&=dx^{\prime 2}+dy^{\prime 2}+dz^{\prime 2}-c^{\prime 2}dt^{\prime 2}\end{aligned}}\end{matrix}}}$

Коттлер (1914а) ${\scriptstyle {\begin{matrix}{\begin{aligned}x^{(1)}&=x_{0}^{(1)}\\x^{(2)}&=x_{0}^{(2)}\\x^{(3)}&=b\cos iu\\x^{(4)}&=b\sin iu\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-c^{2}d\tau ^{2}=b^{2}(du)^{2}\\{\boldsymbol {\downarrow }}\\{\begin{matrix}c_{1}^{(1)}=0,&&c_{1}^{(2)}=0,&&c_{1}^{(3)}=-\sin iu,&&c_{1}^{(4)}=\cos iu,\\c_{2}^{(1)}=0,&&c_{2}^{(2)}=0,&&c_{2}^{(3)}=-\cos iu,&&c_{2}^{(4)}=-\sin iu,\end{matrix}}\\{\boldsymbol {\downarrow }}\\dS^{2}=(dX')^{2}+(dY')^{2}+(dZ')^{2}-\left(c+{\frac {Z'c}{b}}\right)^{2}dT'\\{\boldsymbol {\downarrow }}\\c'=c+{\frac {Z'c^{2}}{b}}\cdot {\frac {1}{c}}\end{matrix}}}$ Коттлер (1914б) $\scriptstyle {\begin{matrix}{\begin{matrix}c_{1}^{(1)}=0,&&c_{1}^{(2)}=0,&&c_{1}^{(3)}={\frac {1}{i}}\sinh u,&&c_{1}^{(4)}=\cosh u,\\c_{2}^{(1)}=0,&&c_{2}^{(2)}=0,&&c_{2}^{(3)}={\frac {1}{i}}\cosh u,&&c_{2}^{(4)}=-\sinh u,\\c_{3}^{(1)}=1,&&c_{3}^{(2)}=0,&&c_{3}^{(3)}=0,&&c_{3}^{(4)}=0,\\c_{4}^{(1)}=0,&&c_{4}^{(2)}=1,&&c_{4}^{(3)}=0,&&c_{4}^{(4)}=0,\end{matrix}}\\{\boldsymbol {\downarrow }}\\X=x+\Delta ^{(2)}c_{2}+\Delta ^{(3)}c_{3}+\Delta ^{(4)}c_{4}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&=x_{0}+{\mathfrak {X}}'\\Y&=y_{0}+{\mathfrak {Y}}'\\Z&=\left(b+{\mathfrak {Z}}'\right)\cosh {\mathfrak {u}}\\cT&=\left(b+{\mathfrak {Z}}'\right)\sinh {\mathfrak {u}}\end{aligned}}\\\left(\Delta ^{(2)}={\mathfrak {X}}',\ \Delta ^{(3)}={\mathfrak {Y}}',\ \Delta ^{(4)}={\mathfrak {Z}}'\right)\\{\boldsymbol {\downarrow }}\\{\begin{aligned}{\mathfrak {X}}'&=X_{0}-x_{0}+q_{x}T\\{\mathfrak {Y}}'&=Y_{0}-y_{0}+q_{y}T\\b+{\mathfrak {Z}}'&={\sqrt {\left(Z_{0}+q_{x}T\right)^{2}-c^{2}T^{2}}}\\c{\mathfrak {T}}'&=b\operatorname {artanh} {\frac {cT}{Z_{0}+q_{x}T}}\end{aligned}}\\\left(X=X_{0}+q_{x}T,\ Y=Y_{0}+q_{y}T,\ Z=Z_{0}+q_{x}T\right)\\{\boldsymbol {\downarrow }}\\dS^{2}=(d{\mathfrak {X}}')^{2}+(d{\mathfrak {Y}}')^{2}+(d{\mathfrak {Z}}')^{2}-c^{2}\left({\frac {b+{\mathfrak {Z}}'}{b^{2}}}\right)^{2}(d{\mathfrak {T}}')^{2}\end{matrix}}$ Коттлер (1916, 1918) $\scriptstyle {\begin{matrix}{\begin{aligned}x&=x'\\y&=y'\\{\frac {c^{2}}{\gamma }}+z&=\left({\frac {c^{2}}{\gamma }}+z'\right)\cosh {\frac {\gamma t'}{c}}\\ct&=\left({\frac {c^{2}}{\gamma }}+z'\right)\sinh {\frac {\gamma t'}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{\prime 2}+dy^{\prime 2}+dz^{\prime 2}-\left(c+{\frac {\gamma }{c}}z'\right){}^{2}dt^{\prime 2}\end{matrix}}$

Паули (1921) $\scriptstyle {\begin{matrix}{\begin{aligned}x^{1}&=\varrho \cos \varphi \\x^{4}&=\varrho \sin \varphi \end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=\left(d\xi ^{1}\right)^{2}+\left(d\xi ^{2}\right)^{2}+\left(d\xi ^{3}\right)^{2}+\left(\xi ^{1}\right)^{2}\left(d\xi ^{4}\right)^{2}\\\left(\xi ^{(1)}=\varrho ,\ \xi ^{(2)}=x^{(2)},\ \xi ^{(3)}=x^{(3)},\ \xi ^{(4)}=\varphi \right)\end{matrix}}$ Боллард (1922) ${\scriptstyle {\begin{matrix}ds^{2}=c^{2}\left(1+{\frac {\gamma _{0}x}{c^{2}}}\right)d\tau ^{2}-dx^{2}-dy^{2}-dz^{2}\\\hline ds^{2}=g_{44}dx_{4}^{2}+g_{11}dx_{1}^{2}+g_{22}\left(dx_{2}^{2}+dx_{3}^{2}\right)\\{\boldsymbol {\downarrow }}\\V''-{\frac {g_{11}}{2g_{11}}}V'=0\\\left(g_{22}=-1,\ g_{11}=-1,\ V''=0,\ V=ax+b\right)\\{\boldsymbol {\downarrow }}\\ds^{2}=dx_{4}^{2}(ax+b)^{2}-dx^{2}-dy^{2}-dz^{2}\end{matrix}}}$ Мохоровичич (1922, 1923); Боллерт (1922b) ${\scriptstyle {\begin{matrix}{\text{Mohorovičić (1922):}}\\g_{11}=g_{44}=V^{2},\ VV''-V'^{2}=0,\ V\left(x_{1}\right)=e^{ax_{1}}\\{\boldsymbol {\downarrow }}\\ds^{2}=e^{2a}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\\\\{\text{corrected by Bollert (1922b):}}\\ds^{2}=e^{2ax}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\\\\{\text{final correction by Mohorovičić (1923):}}\\ds^{2}=e^{2ax_{1}}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\end{matrix}}}$ Леметр (1924) ${\scriptstyle {\begin{matrix}{\begin{aligned}1+g\xi =&(1+gx)\cosh gt\\g\tau =&(1+gx)\sinh gt\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx^{2}-dy^{2}-dz^{2}+(1+gx)^{2}dt^{2}\end{matrix}}}$ Эйнштейн и Розен (1935) $\scriptstyle {\begin{matrix}{\begin{aligned}\xi _{1}&=x_{1}\cosh \alpha x_{4}\\\xi _{2}&=x_{2}\\\xi _{3}&=x_{3}\\\xi _{4}&=x_{1}\sinh \alpha x_{4}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx_{1}^{2}-dx_{2}^{2}-dx_{3}^{2}+\alpha {}^{2}x_{1}^{2}dx_{4}^{2}\end{matrix}}$ Моллер (1952) $\scriptstyle {\begin{matrix}\alpha _{ik}=\left({\begin{matrix}U_{4}/ic&0&0&iU_{1}/c\\0&1&0&0\\0&0&1&0\\U_{1}/ic&0&0&U_{4}/ic\end{matrix}}\right)\\U_{i}=\left(c\sinh {\frac {g\tau }{c}},\ 0,0,\ ig\cosh {\frac {g\tau }{c}}\right)\\{\boldsymbol {\downarrow }}\\X_{i}=\mathbf {f} _{i}(t)+x^{\prime \kappa }\alpha _{\kappa i}(\tau )\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&={\frac {c^{2}}{g}}\left(\cosh {\frac {gt}{c}}-1\right)+x\cosh {\frac {gt}{c}}\\Y&=y\\Z&=z\\T&={\frac {c}{g}}\sinh {\frac {gt}{c}}+x{\frac {\sinh {\frac {gt}{c}}}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}\left(1+gx/c^{2}\right)^{2}\\\\\end{matrix}}$

См. также

• Парадокс космического корабля Белла — иногда спорный вопрос, который часто изучается с использованием координат Риндлера.
• Координаты Борна — еще одна важная система координат, адаптированная к движению некоторых ускоренных наблюдателей в пространстве-времени Минковского .
• Конгруэнтность (общая теория относительности)
• Парадокс Эренфеста , иногда спорный предмет, который часто изучается с использованием координат Борна.
• Поля кадра в общей теории относительности
• Ресурсы по общей теории относительности
• Модель Милна
• Уравнение Райчаудхури
• Эффект Унру

Дальнейшее чтение

Полезный фон:

• Бутби, Уильям М. (1986). Введение в дифференцируемые многообразия и риманову геометрию . Нью-Йорк: Академическая пресса. ISBN  0-12-116052-1 . См. главу 4 для получения дополнительной информации о векторных полях на гладких многообразиях.
• Франкель, Теодор (1979). Гравитационная кривизна: введение в теорию Эйнштейна . Сан-Франциско: WH Freeman. ISBN  0-7167-1062-5 . См. главу 8 для вывода метрики Ферма.

Координаты Риндлера:

• Риндлер, Вольфганг (1969). Основная теория относительности . Нью-Йорк, Ван Ностранд Рейнхольд Ко. doi : 10.1007/978-1-4757-1135-6 . ISBN  978-0-387-90201-2 .

• Миснер, Чарльз; Торн, Кип С. и Уилер, Джон Арчибальд (1973). Гравитация . Сан-Франциско: WH Freeman. ISBN  0-7167-0344-0 . См. раздел 6.6 .
• Риндлер, Вольфганг (2001). Относительность: специальная, общая и космологическая . Оксфорд: Издательство Оксфордского университета. ISBN  0-19-850836-0 .
• Ни, Вэй-Тоу; Циммерманн, Марк (1978). «Инерционные и гравитационные эффекты в собственной системе отсчета ускоренного вращающегося наблюдателя». Физический обзор D . 17 (6): 1473–1476. Бибкод : 1978PhRvD..17.1473N . дои : 10.1103/PhysRevD.17.1473 .

Горизонт Риндлера:

• Джейкобсон, Тед и Паренти, Рено (2003). «Энтропия горизонта». Найденный. Физ . 33 (2): 323–348. arXiv : gr-qc/0302099 . Бибкод : 2003FoPh...33..323J . дои : 10.1023/A:1023785123428 . S2CID   16826867 . электронная версия
• Барсело, Карлос; Либерати, Стефано и Виссер, Мэтт (2005). «Аналоговая гравитация» . Живые обзоры в теории относительности . 8 (1): 12. arXiv : gr-qc/0505065 . Бибкод : 2005LRR.....8...12B . дои : 10.12942/lrr-2005-12 . ПМЦ   5255570 . ПМИД   28179871 .