Гиперболическое движение (относительность)

Гиперболическое движение можно представить на диаграмме Минковского, где движение ускоряющейся частицы происходит вдоль $X$ -ось. Каждая гипербола определяется $x=\pm c^{2}/\alpha$ и $\eta =\alpha \tau /c$ (с $c=1,\alpha =1$ ) в уравнении ( 2 ).

Гиперболическое движение — это движение объекта с постоянным собственным ускорением в специальной теории относительности . Это называется гиперболическим движением, потому что уравнение, описывающее путь объекта в пространстве-времени, представляет собой гиперболу , что можно увидеть, если нанести его на диаграмму Минковского, координаты которой представляют подходящую инерциальную (неускоренную) систему отсчета. можно обогнать, Это движение имеет несколько интересных особенностей, в том числе то, что фотон если дать ему достаточную фору, как можно заключить из диаграммы. ^[1]

История

Герман Минковский (1908) показал связь между точкой на мировой линии и величиной четырехкратного ускорения и «гиперболой кривизны» ( нем . Krümmungshyperbel ). ^[2] В контексте жесткости борновской Макс Борн (1909) впоследствии ввел термин «гиперболическое движение» ( нем . Hyperbelbewegung ) для случая постоянной величины четырехкратного ускорения, затем дал подробное описание заряженных частиц в гиперболическом движении и ввел соответствующая «гиперболически ускоренная система отсчета» ( нем . Hyperbolisch beschleunigtes Bezugsystem ). ^[3] Формулы Борна были упрощены и расширены Арнольдом Зоммерфельдом (1910). ^[4] Ранние обзоры см. в учебниках Макса фон Лауэ (1911, 1921). ^[5] или Вольфганг Паули (1921). ^[6] См. также Галерею (2015). ^[7] или Гургульон (2013), ^[8] и ускорение (специальная теория относительности)#История .

Мировая линия

Правильное ускорение $\alpha$ частицы определяется как ускорение , которое частица «чувствует» при ускорении от одной инерциальной системы отсчета к другой. Если собственное ускорение направлено параллельно линии движения, оно относится к обычному тройному ускорению в специальной теории относительности. $a=du/dT$ к

\alpha =\gamma ^{3}a={\frac {1}{\left(1-u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},

где $u$ - мгновенная скорость частицы, $\gamma$ фактор Лоренца , $c$ это скорость света , а $T$ это координатное время. Решение уравнения движения дает искомые формулы, которые можно выразить через координатное время. $T$ а также подходящее время $\tau$ . Для упрощения все начальные значения времени, местоположения и скорости можно установить равными 0, таким образом: ^[5]^[6]^[9]^[10]^[11]

{\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {\alpha T}{\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}}\\&=c\tanh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)\\X(T)&={\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}-1\right)\\&={\frac {c^{2}}{\alpha }}\left(\cosh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)-1\right)\\c\tau (T)&={\frac {c^{2}}{\alpha }}\ln \left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}+{\frac {\alpha T}{c}}\right)\\&={\frac {c^{2}}{\alpha }}\operatorname {arsinh} {\frac {\alpha T}{c}}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh {\frac {\alpha \tau }{c}}\\\\X(\tau )&={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)\\\\cT(\tau )&={\frac {c^{2}}{\alpha }}\sinh {\frac {\alpha \tau }{c}}\\\\\\\end{aligned}}\end{array}}

( 1 )

Это дает $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ , которая является гиперболой во времени T и переменной пространственного положения $X$ . В этом случае ускоряемый объект находится в точке $X=0$ во время $T=0$ . Если вместо этого имеются начальные значения, отличные от нуля, формулы гиперболического движения принимают вид: ^[12]^[13]^[14]

{\scriptstyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}

Быстрота

Мировую линию гиперболического движения (которая в дальнейшем будет записываться как функция собственного времени) можно упростить несколькими способами. Например, выражение

X={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)

может быть подвергнут пространственному сдвигу суммы $c^{2}/\alpha$ , таким образом

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

, ^[15]

при котором наблюдатель находится в положении $X=c^{2}/\alpha$ во время $T=0$ . Кроме того, установив $x=c^{2}/\alpha$ и введение быстроты $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ , ^[14] уравнения гиперболического движения сводятся к ^[4]^[16]

cT=x\sinh \eta ,\quad X=x\cosh \eta

( 2 )

с гиперболой $X^{2}-c^{2}T^{2}=x^{2}$ .

Заряженные частицы в гиперболическом движении

Родился (1909 г.), ^[3] Летнее поле (1910), ^[4] Лауэ (1911), ^[5] Паули (1921) ^[6] также сформулировал уравнения электромагнитного поля заряженных частиц , находящихся в гиперболическом движении. ^[7] Это было расширено Германом Бонди и Томасом Голдом (1955). ^[17] и Фултон и Рорлих (1960) ^[18]^[19]

{\begin{aligned}E_{\rho '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime 3}}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\\\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^{2}+\left(2\rho '/\alpha \right)^{2}}}\end{aligned}}

Это связано со спорным ^[20]^[21] обсуждаемый вопрос, излучают ли заряды в вечном гиперболическом движении или нет, и соответствует ли это принципу эквивалентности – хотя речь идет об идеальной ситуации, поскольку вечное гиперболическое движение невозможно. В то время как ранние авторы, такие как Борн (1909) или Паули (1921), утверждали, что радиация не возникает, более поздние авторы, такие как Бонди и Голд ^[17] и Фултон и Рорлих ^[18]^[19] показало, что радиация действительно возникает.

Правильная система отсчета

Путь света через E отмечает видимый горизонт событий наблюдателя P в гиперболическом движении.

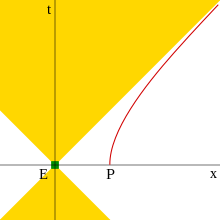
В уравнении ( 2 ) для гиперболического движения выражение $x$ была постоянной, тогда как быстрота $\eta$ был переменным. Однако, как отметил Зоммерфельд, ^[16] можно определить $x$ в качестве переменной, делая $\eta$ постоянный. Это означает, что уравнения становятся преобразованиями, указывающими на одновременную форму покоя ускоренного тела с гиперболическими координатами. $(x,y,z,\eta )$ как видит идущий наблюдатель

cT=x\sinh \eta ,\quad X=x\cosh \eta ,\quad Y=y,\quad Z=z

Посредством этого преобразования собственное время становится временем гиперболически ускоренной системы отсчета. Эти координаты, которые обычно называются координатами Риндлера (подобные варианты называются координатами Коттлера-Мёллера или координатами Ласса ), можно рассматривать как частный случай координат Ферми или собственных координат и часто используются в связи с эффектом Унру . Используя эти координаты, оказывается, что наблюдатели, движущиеся по гиперболическому принципу, обладают кажущимся горизонтом событий , за которым ни один сигнал не может их достичь.

Специальное конформное преобразование

Менее известный метод определения системы отсчета в гиперболическом движении — это использование специального конформного преобразования , состоящего из инверсии , перевода и еще одной инверсии. ^[22] Его обычно интерпретируют как калибровочное преобразование в пространстве Минковского, хотя некоторые авторы альтернативно используют его как преобразование ускорения (критический исторический обзор см. в Каструпе). ^[23] Он имеет форму

X^{\mu }={\frac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}x^{2}}}

Использование только одного пространственного измерения путем $x^{\mu }=(t,x)$ и дальнейшее упрощение, установив $x=0$ , и используя ускорение $a^{\mu }=(0,-\alpha /2)$ , следует ^[24]

T={\frac {t}{1-{\frac {1}{4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {}^{2}t^{2}\right)}}

с гиперболой $\left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}$ . Оказывается, в $t=\pm (x+2/\alpha )$ время становится сингулярным, к чему Фултон, Рорлих и Виттен ^[24] отмечают, что нужно держаться подальше от этого предела, а Каструп ^[23] (который очень критично относится к интерпретации ускорения) отмечает, что это один из странных результатов этой интерпретации.

Примечания

^ Миснер, Торн и Уилер 1973 , Глава 6.
^ Минковский, Герман (1909). «Пространство и время. Лекция, прочитанная на 80-м собрании естествоиспытателей в Кёльне 21 сентября 1908 года» [перевод из Wikisource: Пространство и время ]. Годовой отчет Немецкой ассоциации математиков . Лейпциг.
^ Перейти обратно: ^а ^б Родился Макс (1909). «Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips» [перевод из Wikisource: Теория твердого электрона в кинематике принципа относительности ]. Аннален дер Физик . 335 (11): 1–56. Бибкод : 1909АнП...335....1Б . дои : 10.1002/andp.19093351102 .
^ Перейти обратно: ^а ^б ^с Зоммерфельд, Арнольд (1910). «К теории относительности II: Четырехмерный векторный анализ» [перевод из Wikisource: К теории относительности II: Четырехмерный векторный анализ ]. Анналы физики . 338 (14): 649–689. Бибкод : 1910АнП...338..649С . дои : 10.1002/andp.19103381402 .
^ Перейти обратно: ^а ^б ^с фон Лауэ, М. (1921). Теория относительности, Том 1 (четвертое издание «Принципа относительности» под ред.). Посмотретьег. стр. 89–90 , 155–166. ; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.
^ Перейти обратно: ^а ^б ^с Паули, Вольфганг (1921), «Теория относительности» , Энциклопедия математических наук , 5 (2): 539–776.
По-английски: Паули, В. (1981) [1921]. Теория относительности . Том. 165. Дуврские публикации. ISBN 0-486-64152-Х . {{cite book}}: |journal= игнорируется ( помогите )
^ Перейти обратно: ^а ^б Галериу, К. (2017) [2015]. «Электрический заряд в гиперболическом движении: ранняя история». Архив истории точных наук . 71 (4): 1–16. arXiv : 1509.02504 . дои : 10.1007/s00407-017-0191-x . S2CID 118510589 .
^ Гургульон, Э. (2013). Специальная теория относительности в общих рамках: от частиц к астрофизике . Спрингер. п. 396. ИСБН 978-3642372766 .
^ Мёллер, К. (1955). Теория относительности . Оксфорд Кларендон Пресс. стр. 74–75 .
^ Риндлер, В. (1977). Основная теория относительности . Спрингер. стр. 49–50 . ISBN 354007970X .
^ PhysicsFAQ (2016), «Релятивистская ракета», см. внешние ссылки.
^ Галлант, Дж. (2012). Занятие физикой с помощью научной тетради: подход к решению проблем . Джон Уайли и сыновья. стр. 437–441. ISBN 978-0470665978 .
^ Мюллер Т., Кинг А. и Адис Д. (2006). «Путешествие на край Вселенной и парадокс близнецов ». Американский журнал физики . 76 (4): 360–373. arXiv : физика/0612126 . Бибкод : 2008AmJPh..76..360M . дои : 10.1119/1.2830528 . S2CID 42983285 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Фраундорф, П. (2012). «Введение в кинематику, ориентированное на путешественника»: IV – B. arXiv : 1206.2877 . Бибкод : 2012arXiv1206.2877F . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Паули (1921), с. 628, использовались обозначения $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ где $a={\frac {c^{2}}{b}}$
^ Перейти обратно: ^а ^б Зоммерфельд (1910), стр. 670-671 использует форму $x=r\cos(\varphi )$ и $l=r\sin(\varphi )$ с воображаемым углом $i\psi$ и воображаемое время $l=ict$ .
^ Перейти обратно: ^а ^б Бонди Х. и Голд Т. (1955). «Поле равномерно ускоренного заряда с особым упором на проблему гравитационного ускорения». Труды Лондонского королевского общества . 229 (1178): 416–424. Бибкод : 1955RSPSA.229..416B . дои : 10.1098/rspa.1955.0098 . S2CID 121563673 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Фултон, Томас; Рорлих, Фриц (1960). «Классическое излучение равномерно ускоренного заряда». Анналы физики . 9 (4): 499–517. Бибкод : 1960AnPhy...9..499F . дои : 10.1016/0003-4916(60)90105-6 .
^ Перейти обратно: ^а ^б Рорлих, Фриц (1963). «Принцип эквивалентности». Анналы физики . 22 (2): 169–191. Бибкод : 1963AnPhy..22..169R . дои : 10.1016/0003-4916(63)90051-4 .
^ Стивен Лайл (2008). Равномерно ускоряющиеся заряженные частицы: угроза принципу эквивалентности . Спрингер. ISBN 978-3540684770 .
^ Ойвинд Грён (2012). «Обзорная статья: Электродинамика излучающих зарядов» . Достижения математической физики . 2012 : 528631. doi : 10.1155/2012/528631 . hdl : 10642/1380 .
^ Галериу, Колин (2019) «Электрический заряд в гиперболическом движении: специальное конформное решение», Европейский журнал физики 40 (6) дои : 10.1088/1361-6404/ab3df6
^ Перейти обратно: ^а ^б Каструп, Х.А. (2008). «О достижениях конформных преобразований и связанных с ними симметрий в геометрии и теоретической физике». Аннален дер Физик . 520 (9–10): 631–690. arXiv : 0808.2730 . Бибкод : 2008АнП...520..631К . дои : 10.1002/andp.200810324 . S2CID 12020510 .
^ Перейти обратно: ^а ^б Фултон Т., Рорлих Ф. и Виттен Л. (1962). «Физические последствия преобразования координат в равномерно ускоряющуюся систему отсчета». Иль Нуово Чименто . 26 (4): 652–671. Бибкод : 1962NCim...26..652F . дои : 10.1007/BF02781794 . S2CID 121467786 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

Ссылки

Ли Пейдж (февраль 1936 г.). «Новая теория относительности. Статья I. Фундаментальные принципы и преобразования между ускоренными системами». Физический обзор . 49 (3): 254–268. Бибкод : 1936PhRv...49..254P . дои : 10.1103/PhysRev.49.254 .
Ли Пейдж и Норман И. Адамс (март 1936 г.). «Новая теория относительности. Статья II. Преобразование электромагнитного поля между ускоренными системами и уравнение силы». Физический обзор . 49 (6): 466–469. Бибкод : 1936PhRv...49..466P . дои : 10.1103/PhysRev.49.466 .
Миснер, Чарльз В .; Торн, Кип. С .; Уилер, Джон А. (1973), Гравитация , WH Freeman, глава 6, ISBN 0-7167-0344-0
Риндлер Вольфганг (1960). «Гиперболическое движение в искривленном пространстве-времени». Физический обзор . 119 (6): 2082–2089. Бибкод : 1960PhRv..119.2082R . дои : 10.1103/PhysRev.119.2082 .
Людвик Зильберштейн (1914): Теория относительности , стр. 190.
Набер, Грегори Л., Геометрия пространства-времени Минковского , Springer-Verlag, Нью-Йорк, 1992. ISBN 0-387-97848-8 (твердый переплет), ISBN 0-486-43235-1 (Дуврское издание в мягкой обложке). стр. 58–60.

Внешние ссылки

Часто задаваемые вопросы по физике: Релятивистская ракета
Mathpages: ускоренные путешествия , излучает ли равномерно ускоряющийся заряд?

[1] Миснер, Торн и Уилер 1973 , Глава 6.

[2] Минковский, Герман (1909). «Пространство и время. Лекция, прочитанная на 80-м собрании естествоиспытателей в Кёльне 21 сентября 1908 года» [перевод из Wikisource: Пространство и время ]. Годовой отчет Немецкой ассоциации математиков . Лейпциг.

[born-3] Перейти обратно: ^а ^б Родился Макс (1909). «Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips» [перевод из Wikisource: Теория твердого электрона в кинематике принципа относительности ]. Аннален дер Физик . 335 (11): 1–56. Бибкод : 1909АнП...335....1Б . дои : 10.1002/andp.19093351102 .

[sommerfeld-4] Перейти обратно: ^а ^б ^с Зоммерфельд, Арнольд (1910). «К теории относительности II: Четырехмерный векторный анализ» [перевод из Wikisource: К теории относительности II: Четырехмерный векторный анализ ]. Анналы физики . 338 (14): 649–689. Бибкод : 1910АнП...338..649С . дои : 10.1002/andp.19103381402 .

[laue-5] Перейти обратно: ^а ^б ^с фон Лауэ, М. (1921). Теория относительности, Том 1 (четвертое издание «Принципа относительности» под ред.). Посмотретьег. стр. 89–90 , 155–166. ; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.

[pauli-6] Перейти обратно: ^а ^б ^с Паули, Вольфганг (1921), «Теория относительности» , Энциклопедия математических наук , 5 (2): 539–776.
По-английски: Паули, В. (1981) [1921]. Теория относительности . Том. 165. Дуврские публикации. ISBN 0-486-64152-Х . {{cite book}}: |journal= игнорируется ( помогите )

[Galeriu-7] Перейти обратно: ^а ^б Галериу, К. (2017) [2015]. «Электрический заряд в гиперболическом движении: ранняя история». Архив истории точных наук . 71 (4): 1–16. arXiv : 1509.02504 . дои : 10.1007/s00407-017-0191-x . S2CID 118510589 .

[8] Гургульон, Э. (2013). Специальная теория относительности в общих рамках: от частиц к астрофизике . Спрингер. п. 396. ИСБН 978-3642372766 .

[9] Мёллер, К. (1955). Теория относительности . Оксфорд Кларендон Пресс. стр. 74–75 .

[10] Риндлер, В. (1977). Основная теория относительности . Спрингер. стр. 49–50 . ISBN 354007970X .

[11] PhysicsFAQ (2016), «Релятивистская ракета», см. внешние ссылки.

[12] Галлант, Дж. (2012). Занятие физикой с помощью научной тетради: подход к решению проблем . Джон Уайли и сыновья. стр. 437–441. ISBN 978-0470665978 .

[13] Мюллер Т., Кинг А. и Адис Д. (2006). «Путешествие на край Вселенной и парадокс близнецов ». Американский журнал физики . 76 (4): 360–373. arXiv : физика/0612126 . Бибкод : 2008AmJPh..76..360M . дои : 10.1119/1.2830528 . S2CID 42983285 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[fraundorf-14] Перейти обратно: ^а ^б Фраундорф, П. (2012). «Введение в кинематику, ориентированное на путешественника»: IV – B. arXiv : 1206.2877 . Бибкод : 2012arXiv1206.2877F . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[15] Паули (1921), с. 628, использовались обозначения $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ где $a={\frac {c^{2}}{b}}$

[sommerfeld2-16] Перейти обратно: ^а ^б Зоммерфельд (1910), стр. 670-671 использует форму $x=r\cos(\varphi )$ и $l=r\sin(\varphi )$ с воображаемым углом $i\psi$ и воображаемое время $l=ict$ .

[Bondi-17] Перейти обратно: ^а ^б Бонди Х. и Голд Т. (1955). «Поле равномерно ускоренного заряда с особым упором на проблему гравитационного ускорения». Труды Лондонского королевского общества . 229 (1178): 416–424. Бибкод : 1955RSPSA.229..416B . дои : 10.1098/rspa.1955.0098 . S2CID 121563673 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[Fulton-18] Перейти обратно: ^а ^б Фултон, Томас; Рорлих, Фриц (1960). «Классическое излучение равномерно ускоренного заряда». Анналы физики . 9 (4): 499–517. Бибкод : 1960AnPhy...9..499F . дои : 10.1016/0003-4916(60)90105-6 .

[Rohrlich-19] Перейти обратно: ^а ^б Рорлих, Фриц (1963). «Принцип эквивалентности». Анналы физики . 22 (2): 169–191. Бибкод : 1963AnPhy..22..169R . дои : 10.1016/0003-4916(63)90051-4 .

[Lyle-20] Стивен Лайл (2008). Равномерно ускоряющиеся заряженные частицы: угроза принципу эквивалентности . Спрингер. ISBN 978-3540684770 .

[Gron3-21] Ойвинд Грён (2012). «Обзорная статья: Электродинамика излучающих зарядов» . Достижения математической физики . 2012 : 528631. doi : 10.1155/2012/528631 . hdl : 10642/1380 .

[22] Галериу, Колин (2019) «Электрический заряд в гиперболическом движении: специальное конформное решение», Европейский журнал физики 40 (6) дои : 10.1088/1361-6404/ab3df6

[kastrup-23] Перейти обратно: ^а ^б Каструп, Х.А. (2008). «О достижениях конформных преобразований и связанных с ними симметрий в геометрии и теоретической физике». Аннален дер Физик . 520 (9–10): 631–690. arXiv : 0808.2730 . Бибкод : 2008АнП...520..631К . дои : 10.1002/andp.200810324 . S2CID 12020510 .

[Fulton2-24] Перейти обратно: ^а ^б Фултон Т., Рорлих Ф. и Виттен Л. (1962). «Физические последствия преобразования координат в равномерно ускоряющуюся систему отсчета». Иль Нуово Чименто . 26 (4): 652–671. Бибкод : 1962NCim...26..652F . дои : 10.1007/BF02781794 . S2CID 121467786 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]