Инерциальная система отсчета

В классической физике система отсчета ( и специальной теории относительности инерциальная также называемая инерциальным пространством или системой отсчета Галилея ) — это стационарная или равномерно движущаяся система отсчета . С этой точки зрения объекты покоятся до тех пор, пока на них не воздействуют внешние силы, и законы природы можно наблюдать без необходимости коррекции ускорения.

Все системы отсчета с нулевым ускорением находятся в состоянии постоянного прямолинейного движения (прямолинейного движения) относительно друг друга. В такой системе отсчета объект с нулевой результирующей силой, действующей на него, воспринимается как движущийся с постоянной скоростью или, что то же самое, соблюдается первый закон движения Ньютона . Это системы, называемые инерциальными. Первоначально некоторые физики, такие как Исаак Ньютон, считали, что одна из этих систем отсчета является абсолютной — той, которая аппроксимируется неподвижными звездами . Однако для определения это не требуется, и теперь известно, что эти звезды на самом деле движутся.

Согласно специальному принципу относительности , все физические законы выглядят одинаково во всех инерциальных системах отсчета, и ни одна инерциальная система не имеет преимущества перед другой. Измерения объектов в одной инерциальной системе отсчета можно преобразовать в измерения в другой с помощью простого преобразования — преобразования Галилея в физике Ньютона или преобразования Лоренца (в сочетании со сдвигом) в специальной теории относительности ; они примерно совпадают, когда относительная скорость кадров низкая, но различаются по мере приближения к скорости света .

Напротив, неинерциальная система отсчета имеет ненулевое ускорение. В такой системе отсчета взаимодействие между физическими объектами варьируется в зависимости от ускорения этой системы отсчета по отношению к инерциальной системе отсчета. С точки зрения классической механики и специальной теории относительности «обычные» физические силы, вызванные взаимодействием объектов, должны быть дополнены фиктивными силами, вызванными инерцией . С точки зрения общей теории относительности , инерционные (т.е. фиктивные) силы приписываются геодезическому движению в пространстве-времени .

Из-за вращения Земли ее поверхность не является инерциальной системой отсчета. Эффект Кориолиса может отклонять определенные формы движения, наблюдаемые с Земли , а центробежная сила уменьшит эффективную гравитацию на экваторе . Тем не менее, Земля является хорошим приближением инерциальной системы отсчета, подходящей для многих приложений.

Введение

Движение тела можно описать только относительно чего-то другого — других тел, наблюдателей или набора пространственно-временных координат. Это так называемые системы отсчета . Согласно первому постулату специальной теории относительности , все физические законы принимают простейшую форму в инерциальной системе отсчета, и существует множество инерциальных систем отсчета, связанных между собой равномерным перемещением :

Специальный принцип относительности: если система координат K выбрана так, что по отношению к ней действуют физические законы в своей простейшей форме, то те же законы справедливы и по отношению к любой другой системе координат K', движущейся равномерно поступательно относительно к К.

- Альберт Эйнштейн: Основы общей теории относительности , Раздел A, §1.

Эта простота проявляется в том, что инерциальные системы отсчета имеют самодостаточную физику без необходимости внешних причин, тогда как физика в неинерциальных системах отсчета имеет внешние причины. Принцип простоты можно использовать как в ньютоновской физике, так и в специальной теории относительности:

Законы ньютоновской механики не всегда выполняются в своей простейшей форме... Если, например, наблюдателя поместить на диск, вращающийся относительно Земли, он/она почувствует «силу», толкающую его/ее к периферии. диска, не вызванное каким-либо взаимодействием с другими телами. Здесь ускорение является следствием не обычной силы, а так называемой силы инерции. Законы Ньютона в своей простейшей форме справедливы только в семействе систем отсчета, называемых инерциальными системами отсчета. Этот факт отражает суть принципа относительности Галилея:
Законы механики имеют одинаковую форму во всех инерциальных системах отсчета.

- Милутин Благоевич: Гравитация и калибровочные симметрии , стр. 4.

Однако считается, что это определение инерциальной системы отсчета применимо в ньютоновской сфере и игнорирует релятивистские эффекты.

На практике эквивалентность инерциальных систем отсчета означает, что ученые внутри коробки, движущейся с постоянной абсолютной скоростью, не могут определить эту скорость каким-либо экспериментом. В противном случае различия создали бы абсолютную стандартную систему отсчета. Согласно этому определению, дополненному постоянством скорости света, инерциальные системы отсчета преобразуются между собой по группе преобразований симметрии Пуанкаре которой являются преобразования Лоренца . , подгруппой В механике Ньютона инерциальные системы отсчета связаны группой Галилея симметрий .

Инерциальная система отсчета Ньютона

Абсолютное пространство

Основная статья: Абсолютное пространство и время

Ньютон постулировал, что абсолютное пространство считается хорошо аппроксимируемым системой отсчета, стационарной относительно неподвижных звезд . Инерциальная система отсчета тогда находилась в равномерном перемещении относительно абсолютного пространства. Однако некоторые «релятивисты», даже во времена Ньютона считал, что абсолютное пространство является дефектом формулировки и его следует заменить.

Выражение «инерциальная система отсчета» ( нем . Inertialsystem ) было придумано Людвигом Ланге в 1885 году, чтобы заменить определения Ньютона «абсолютного пространства и времени» более оперативным определением :

Система отсчета, в которой массовая точка, брошенная из одной и той же точки в трех разных (некомпланарных) направлениях, каждый раз при броске следует по прямолинейным траекториям, называется инерциальной системой отсчета.

Неадекватность понятия «абсолютного пространства» в механике Ньютона подчеркивает Благоевич:

• Существование абсолютного пространства противоречит внутренней логике классической механики, поскольку, согласно принципу относительности Галилея, ни одна из инерциальных систем отсчета не может быть выделена.
• Абсолютное пространство не объясняет силы инерции, поскольку они связаны с ускорением по отношению к любой из инерциальных систем отсчета.
• Абсолютное пространство действует на физические объекты, вызывая их сопротивление ускорению, но на него невозможно воздействовать.

- Милутин Благоевич: Гравитация и калибровочные симметрии , стр. 5.

Полезность операционных определений получила гораздо большее развитие в специальной теории относительности. Некоторая историческая справка, включая определение Ланге, предоставлена ​​ДиСалле, который вкратце говорит:

Исходный вопрос: «Относительно какой системы отсчета действуют законы движения?» оказывается неправильно поставленным. Законы движения по существу определяют класс систем отсчета и (в принципе) процедуру их построения.

- Роберт ДиСалле Пространство и время: инерциальные системы отсчета

Ньютоновская механика

Классические теории, использующие преобразование Галилея, постулируют эквивалентность всех инерциальных систем отсчета. Преобразование Галилея преобразует координаты из одной инерциальной системы отсчета, $\mathbf {s}$, другому, $\mathbf {s} ^{\prime }$, простым сложением или вычитанием координат:

$\mathbf {r} ^{\prime }=\mathbf {r} -\mathbf {r} _{0}-\mathbf {v} t$

$t^{\prime }=t-t_{0}$

где r ₀ и t ₀ представляют собой сдвиги в начале координат пространства и времени, а v - относительная скорость двух инерциальных систем отсчета. При преобразованиях Галилея время t ₂ − t ₁ между двумя событиями одинаково для всех систем отсчета, а расстояние между двумя одновременными событиями (или, что то же самое, длина любого объекта | r ₂ − r ₁ |) также является такой же.

Рисунок 1 : Две системы отсчета, движущиеся с относительной скоростью. ${\stackrel {\vec {v}}{}}$. Кадр S' но фиксированное вращение относительно кадра S. имеет произвольное , Обе системы являются инерциальными , если кажется, что тело, на которое не действуют силы, движется по прямой. Если это движение видно в одном кадре, оно будет таким же и в другом.

В сфере ньютоновской механики инерциальная система отсчета или инерциальная система отсчета — это система, в которой первый закон движения Ньютона . действует Однако принцип специальной теории относительности обобщает понятие инерциальной системы отсчета, включив в него все физические законы, а не только первый закон Ньютона.

Ньютон считал, что первый закон действует в любой системе отсчета, которая находится в равномерном движении (не вращающемся и не ускоряющемся) относительно абсолютного пространства ; на практике «абсолютным пространством» считались неподвижные звезды. В теории относительности отбрасывается понятие абсолютного пространства или привилегированной системы отсчета , а инерциальная система отсчета в области классической механики определяется как:

Инерциальная система отсчета — это система, в которой движение частицы, не подверженной действию сил, происходит по прямой линии с постоянной скоростью.

Следовательно, относительно инерциальной системы отсчета объект или тело ускоряется физическая сила только тогда, когда приложена , и (следуя первому закону движения Ньютона ) в отсутствие чистой силы тело, находящееся в состоянии покоя, останется в покое, а тело, находящееся в движении, будет продолжать двигаться равномерно, то есть прямолинейно и с постоянной скоростью . Ньютоновские инерциальные системы отсчета преобразуются между собой согласно группе симметрий Галилея .

Если это правило интерпретируется как говорящее, что прямолинейное движение является показателем нулевой результирующей силы, это правило не идентифицирует инерциальные системы отсчета, поскольку прямолинейное движение можно наблюдать в различных кадрах. Если правило интерпретируется как определение инерциальной системы координат, то решающее значение имеет возможность определить, когда применяется нулевая чистая сила. Эту проблему резюмировал Эйнштейн:

Слабость принципа инерции состоит в том, что он предполагает рассуждение по кругу: масса движется без ускорения, если она находится достаточно далеко от других тел; мы знаем, что оно достаточно далеко от других тел только потому, что оно движется без ускорения.

- Альберт Эйнштейн: Значение теории относительности , с. 58

Существует несколько подходов к этому вопросу. Один из подходов состоит в том, чтобы утверждать, что все реальные силы известным образом спадают с расстоянием от своих источников, поэтому необходимо только, чтобы тело находилось достаточно далеко от всех источников, чтобы гарантировать отсутствие силы. Возможная проблема с этим подходом заключается в исторически давнем представлении о том, что далекая Вселенная может влиять на ситуацию ( принцип Маха ). Другой подход заключается в выявлении всех реальных источников реальных сил и их учете. Возможная проблема с этим подходом — возможность что-то упустить или неправильно учесть их влияние, возможно, опять же, из-за принципа Маха и неполного понимания Вселенной. Третий подход состоит в том, чтобы посмотреть, как трансформируются силы при сдвиге системы отсчета. Фиктивные силы, возникающие вследствие ускорения системы отсчета, исчезают в инерциальных системах отсчета и в общих случаях имеют сложные правила преобразования. Ввиду универсальности физических законов и требования к системам, в которых законы выражаются наиболее просто, инерционные системы отличаются отсутствием таких фиктивных сил.

Ньютон сам сформулировал принцип относительности в одном из своих следствий из законов движения:

Движения тел, входящих в данное пространство, одинаковы между собой, независимо от того, покоится ли это пространство или движется равномерно вперед по прямой.

- Исаак Ньютон: Начала , следствие V, с. 88 в переводе Эндрю Мотта

Этот принцип отличается от специального принципа в двух отношениях: во-первых, он ограничивается механикой, а во-вторых, в нем не упоминается простота. Он разделяет особый принцип инвариантности формы описания среди взаимопереводящих систем отсчета. Роль фиктивных сил в классификации систем отсчета рассматривается ниже.

Специальная теория относительности

Основная статья: Специальная теория относительности

Эйнштейна Специальная теория относительности , как и механика Ньютона, постулирует эквивалентность всех инерциальных систем отсчета. Однако, поскольку специальная теория относительности постулирует, что света в свободном пространстве инвариантна скорость , преобразование между инерциальными системами отсчета является преобразованием Лоренца , а не преобразованием Галилея , которое используется в механике Ньютона.

Инвариантность скорости света приводит к парадоксальным явлениям, таким как замедление времени , сокращение длины и относительность одновременности . Предсказания специальной теории относительности были тщательно проверены экспериментально. Преобразование Лоренца сводится к преобразованию Галилея, когда скорость света приближается к бесконечности или когда относительная скорость между кадрами приближается к нулю.

Примеры

Простой пример

Рисунок 1 : Два автомобиля, движущиеся с разными, но постоянными скоростями, наблюдаемые из неподвижной инерциальной системы S, прикрепленной к дороге, и движущейся инерционной системы S', прикрепленной к первой машине.

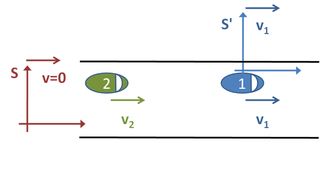
Рассмотрим ситуацию, распространенную в повседневной жизни. Два автомобиля едут по дороге, причем оба движутся с постоянной скоростью. См. рисунок 1. В какой-то конкретный момент их разделяют 200 метров. Автомобиль впереди движется со скоростью 22 метра в секунду, а автомобиль сзади — со скоростью 30 метров в секунду. Если мы хотим узнать, сколько времени понадобится второй машине, чтобы догнать первую, мы можем выбрать три очевидные «системы отсчета».

Сначала мы могли наблюдать за двумя машинами со стороны дороги. Мы определяем нашу «систему отсчета» S следующим образом. Мы стоим на обочине дороги и запускаем секундомер именно в тот момент, когда нас проезжает вторая машина, а это происходит, когда они находятся на расстоянии d = 200 м друг от друга. Поскольку ни один из автомобилей не ускоряется, мы можем определить их положение по следующим формулам, где $x_{1}(t)$ - положение автомобиля в метрах после времени t в секундах и $x_{2}(t)$ — положение второго автомобиля по истечении времени t .

$x_{1}(t)=d+v_{1}t=200+22t,\quad x_{2}(t)=v_{2}t=30t.$

Обратите внимание, что эти формулы предсказывают, что в момент времени t = 0 с первая машина находится в 200 м по дороге, а вторая машина, как и ожидалось, находится рядом с нами. Мы хотим найти время, в которое $x_{1}=x_{2}$. Поэтому мы установили $x_{1}=x_{2}$ и решить для $t$, то есть:

$200+22t=30t,$

$8t=200,$

$t=25\ \mathrm {seconds} .$

В качестве альтернативы мы могли бы выбрать систему отсчета S', расположенную в первом автомобиле. В этом случае первый автомобиль стоит, а второй приближается сзади со скоростью v ₂ − v ₁ = 8 м/с . Чтобы догнать первую машину, потребуется время ⁠ d / v ₂ - v ₁ ⁠ знак равно ⁠ 200/8 . ⁠ с , то есть 25 секунд, как и раньше Обратите внимание, насколько проще становится проблема, если выбрать подходящую систему отсчета. Третья возможная система отсчета будет прикреплена ко второй машине. Этот пример напоминает только что рассмотренный случай, за исключением того, что второй автомобиль стоит на месте, а первый движется назад к нему со скоростью 8 м/с .

Можно было бы выбрать вращающуюся, ускоряющуюся систему отсчета, движущуюся сложным образом, но это излишне усложнило бы задачу. Также необходимо отметить, что можно преобразовать измерения, выполненные в одной системе координат, в другую. Например, предположим, что ваши часы идут на пять минут быстрее по сравнению с местным стандартным временем. Если вы знаете, что это так, то когда кто-то спрашивает вас, сколько сейчас времени, вы можете вычесть пять минут из времени, отображаемого на ваших часах, чтобы получить правильное время. Таким образом, измерения, которые наблюдатель производит в отношении системы, зависят от системы отсчета наблюдателя (вы можете сказать, что автобус прибыл в 5 минут четвертого, хотя на самом деле он прибыл в три).

Дополнительный пример

Рисунок 2. Простой пример системы отсчета.

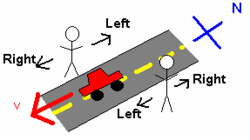
В качестве простого примера, включающего только ориентацию двух наблюдателей, рассмотрим двух человек, стоящих лицом друг к другу по обе стороны улицы, идущей с севера на юг. См. рисунок 2. Мимо них проезжает машина, направляясь на юг. Для человека, смотрящего на восток, машина двигалась вправо. Однако для человека, смотрящего на запад, машина двигалась влево. Это несоответствие связано с тем, что эти два человека использовали две разные системы координат для исследования этой системы.

В качестве более сложного примера, включающего наблюдателей в относительном движении, рассмотрим Альфреда, который стоит на обочине дороги и наблюдает, как мимо него слева направо проезжает машина. В своей системе отсчета Альфред определяет место, где он стоит, как начало координат, дорогу как ось X , а направление перед ним как положительную Y. ось По его мнению, автомобиль движется вдоль оси x с некоторой скоростью v в положительном направлении x . Система отсчета Альфреда считается инерциальной, потому что он не ускоряется и игнорирует такие эффекты, как вращение Земли и гравитация.

Теперь рассмотрим Бетси, человека, который ведет машину. Бетси, выбирая систему отсчета, определяет свое местоположение как начало координат, направление вправо от нее — как положительную ось X , а направление перед ней — как положительную Y. ось В этой системе отсчета Бетси неподвижна, а мир вокруг нее движется - например, проезжая мимо Альфреда, она наблюдает, как он движется со скоростью v в отрицательном направлении y . Если она едет на север, то север — это положительное направление по оси Y ; если она повернется на восток, восток станет положительным Y. направлением

Наконец, в качестве примера неинерциальных наблюдателей предположим, что Кэндис ускоряет свою машину. Когда она проходит мимо него, Альфред измеряет ее ускорение и обнаруживает, что оно направлено в отрицательном направлении x . Если предположить, что ускорение Кэндис постоянно, какое ускорение измеряет Бетси? Бетси Если скорость v постоянна, она находится в инерциальной системе отсчета и обнаружит, что ускорение такое же, как у Альфреда в ее системе отсчета, а в отрицательном направлении y . Однако, если она ускоряется со скоростью A в отрицательном направлении y (другими словами, замедляется), она обнаружит, что ускорение Кэндис равно a' = a - A в отрицательном направлении y - меньшее значение, чем у Альфреда. измерено. Точно так же, если она ускоряется со скоростью A в положительном направлении y (ускорение), она будет наблюдать ускорение Кэндис как a ' = a + A в отрицательном направлении y - большее значение, чем измерение Альфреда.

Неинерциальные рамки

Основные статьи: Фиктивная сила , Неинерциальная система отсчета и Вращающаяся система отсчета.

Здесь рассматривается соотношение между инерциальными и неинерциальными системами отсчета. Основное различие между этими системами координат заключается в необходимости использования в неинерциальных системах фиктивных сил, как описано ниже.

Общая теория относительности

Основные статьи: Общая теория относительности и Введение в общую теорию относительности.

Смотрите также: Принцип эквивалентности и эксперимент Этвеша.

Общая теория относительности основана на принципе эквивалентности:

Наблюдатели не могут провести эксперимент, чтобы определить, возникает ли ускорение из-за гравитационной силы или из-за того, что их система отсчета ускоряется.

- Дуглас К. Джанколи, Физика для ученых и инженеров с современной физикой , с. 155.

Эта идея была представлена ​​в статье Эйнштейна 1907 года «Принцип относительности и гравитации» и позже развита в 1911 году. Подтверждение этому принципу находится в эксперименте Этвёша , который определяет, одинаково ли соотношение инертной и гравитационной массы для всех тел, независимо от размера и состава. На сегодняшний день не обнаружено различий для нескольких частей из 10. ¹¹ . Некоторое обсуждение тонкостей эксперимента Этвёша, таких как локальное распределение массы вокруг экспериментальной площадки (включая шутку о массе самого Этвёша), см. у Франклина.

Эйнштейна Общая теория изменяет различие между номинально «инерционными» и «неинерциальными» эффектами, заменяя «плоское» пространство Минковского специальной теории относительности метрикой, которая создает ненулевую кривизну. В общей теории относительности принцип инерции заменяется принципом геодезического движения , согласно которому объекты движутся в соответствии с кривизной пространства-времени. Вследствие этой кривизны в общей теории относительности не является данностью, что инерционные объекты, движущиеся с определенной скоростью относительно друг друга, будут продолжать это делать. Это явление геодезического отклонения означает, что инерциальные системы отсчета не существуют глобально, как в механике Ньютона и специальной теории относительности.

Однако общая теория сводится к специальной теории в достаточно малых областях пространства-времени, где эффекты кривизны становятся менее важными и более ранние аргументы об инерциальной системе отсчета могут вернуться в игру. Следовательно, современную специальную теорию относительности теперь иногда называют всего лишь «локальной теорией». «Местное» может охватывать, например, всю галактику Млечный Путь: астроном Карл Шварцшильд наблюдал движение пар звезд, вращающихся вокруг друг друга. Он обнаружил, что две орбиты звезд такой системы лежат в плоскости, а перигелий орбит двух звезд остается направленным в одном направлении по отношению к Солнечной системе . Шварцшильд указывал, что это наблюдалось неизменно: направление момента количества движения всех наблюдаемых двойных звездных систем остается фиксированным по отношению к направлению момента количества движения Солнечной системы. Эти наблюдения позволили ему сделать вывод, что инерциальные системы отсчета внутри галактики не вращаются относительно друг друга и что пространство Млечного Пути примерно галилеевское или минковское.

Инерциальные системы отсчета и вращение

В инерциальной системе отсчета первый закон Ньютона , закон инерции : любое свободное движение имеет постоянную величину и направление. соблюдается Второй закон Ньютона для частицы имеет вид:

$\mathbf {F} =m\mathbf {a} \ ,$

где F - чистая сила ( вектор ), m - масса частицы и a - частицы ускорение (также вектор), которое будет измерено наблюдателем, покоящимся в системе отсчета. Сила F представляет собой векторную сумму всех «реальных» сил, действующих на частицу, таких как контактные силы , электромагнитные, гравитационные и ядерные силы.

Напротив, второй закон Ньютона во вращающейся системе отсчета ( неинерциальной системе отсчета ), вращающейся с угловой скоростью Ω вокруг оси, принимает форму:

$\mathbf {F} '=m\mathbf {a} \ ,$

которое выглядит так же, как и в инерциальной системе отсчета, но теперь сила F ′ является равнодействующей не только F , но и дополнительных слагаемых (в абзаце, следующем за этим уравнением, представлены основные моменты без подробной математики):

$\mathbf {F} '=\mathbf {F} -2m\mathbf {\Omega } \times \mathbf {v} _{B}-m\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {x} _{B})-m{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {x} _{B}\ ,$

где угловое вращение системы координат выражается вектором Ω, направленным в направлении оси вращения, и с величиной, равной угловой скорости вращения Ω , символ × обозначает векторное векторное произведение , вектор x _B определяет местоположение тела и вектор v _B — скорость тела по мнению вращающегося наблюдателя (отличная от скорости, которую видит инерциальный наблюдатель).

Дополнительные члены в силе F ′ являются «фиктивными» силами для этой системы отсчета, причины которых являются внешними по отношению к системе в системе отсчета. Первый дополнительный член — это сила Кориолиса , второй — центробежная сила , а третий — сила Эйлера . Все эти члены обладают следующими свойствами: они исчезают, когда Ω = 0; то есть они равны нулю для инерциальной системы отсчета (которая, конечно, не вращается); они принимают разную величину и направление в каждой вращающейся системе отсчета, в зависимости от ее конкретного значения Ω ; они повсеместно распространены во вращающейся системе отсчета (воздействуют на каждую частицу независимо от обстоятельств); и у них нет очевидного источника в идентифицируемых физических источниках, в частности, в материи . Кроме того, фиктивные силы не спадают с расстоянием (в отличие, например, от ядерных или электрических сил ). Например, центробежная сила, которая исходит от оси вращения во вращающейся системе отсчета, увеличивается с расстоянием от оси.

Все наблюдатели согласны с реальными силами F ; фиктивные силы нужны только неинерционным наблюдателям. Законы физики в инерциальной системе отсчета проще, поскольку нет ненужных сил.

Во времена Ньютона неподвижные звезды использовались в качестве системы отсчета, предположительно покоящейся относительно абсолютного пространства . В системах отсчета, которые либо находились в покое относительно неподвижных звезд, либо находились в равномерном перемещении относительно этих звезд, законы движения Ньютона должны были соблюдаться . Напротив, в системах с ускорением относительно неподвижных звезд (важным случаем являются системы, вращающиеся относительно неподвижных звезд), законы движения не выполнялись в своей простейшей форме, а должны были быть дополнены добавлением фиктивных сил , поскольку Например, сила Кориолиса и центробежная сила . Два эксперимента были предложены Ньютоном, чтобы продемонстрировать, как можно обнаружить эти силы, открыв тем самым наблюдателю, что они не находятся в инерциальной системе отсчета: пример натяжения шнура, соединяющего две сферы, вращающиеся вокруг своего центра тяжести, и пример кривизны поверхности воды во вращающемся ведре . В обоих случаях применение второго закона Ньютона не будет работать для вращающегося наблюдателя без привлечения центробежных сил и сил Кориолиса для объяснения их наблюдений (натяжение в случае сфер; параболическая поверхность воды в случае вращающегося ведра).

Как теперь известно, неподвижные звезды не являются фиксированными. Те, что находятся в Млечном Пути, вращаются вместе с галактикой, демонстрируя собственные движения . Те, что находятся за пределами нашей галактики (например, туманности, когда-то ошибочно принятые за звезды), также участвуют в собственном движении, частично из-за расширения Вселенной , а частично из-за пекулярных скоростей . Например, Галактика Андромеды движется к столкновению с Млечным Путем со скоростью 117 км/с. Концепция инерциальных систем отсчета больше не привязана ни к неподвижным звездам, ни к абсолютному пространству. Скорее, идентификация инерциальной системы отсчета основана на простоте законов физики в этой системе отсчета. Законы природы принимают более простую форму в инерциальных системах отсчета, поскольку в этих системах не нужно было вводить силы инерции при записи закона движения Ньютона.

На практике использование системы отсчета, основанной на неподвижных звездах, как если бы это была инерциальная система отсчета, не приводит к небольшому расхождению. Например, центробежное ускорение Земли из-за ее вращения вокруг Солнца примерно в тридцать миллионов раз больше, чем ускорение Солнца вокруг центра Галактики.

Для иллюстрации рассмотрим вопрос: «Вращается ли Вселенная?» Ответ мог бы объяснить форму галактики Млечный Путь , используя законы физики. хотя другие наблюдения могли бы быть более определенными; то есть обеспечить большие расхождения или меньшую неопределенность измерений , как, например, анизотропия микроволнового фонового излучения или нуклеосинтез Большого взрыва . Плоскостность Млечного Пути зависит от скорости его вращения в инерциальной системе отсчета. Если его видимая скорость вращения полностью объясняется вращением в инерциальной системе отсчета, то предсказывается иная «плоскостность», чем если бы предположить, что часть этого вращения на самом деле обусловлена ​​вращением Вселенной и не должна включаться в вращение Вселенной. сама галактика. На основе законов физики создается модель, в которой одним параметром является скорость вращения Вселенной. Если законы физики более точно согласуются с наблюдениями в модели с вращением, чем без него, мы склонны выбирать наиболее подходящее значение вращения с учетом всех других соответствующих экспериментальных наблюдений. Если ни одно значение параметра вращения не является успешным и теория выходит за пределы ошибки наблюдения, рассматривается модификация физического закона, например, темная материя используется для объяснения кривой вращения галактики . На данный момент наблюдения показывают, что любое вращение Вселенной происходит очень медленно, не быстрее, чем один раз в 6 × 10 ¹³ лет (10 ⁻¹³ рад/год), и продолжаются споры о том, есть ли какая-либо ротация. Однако если бы вращение было обнаружено, интерпретацию наблюдений в системе, привязанной к Вселенной, пришлось бы корректировать за фиктивные силы, присущие такому вращению в классической физике и специальной теории относительности, или интерпретировать как искривление пространства-времени и движение материи по нему. геодезические в общей теории относительности.

Когда квантовые эффекты важны, возникают дополнительные концептуальные сложности в квантовых системах отсчета .

Грунтованные рамы

Ускоренная система отсчета часто обозначается как «штрихованная» система координат, и все переменные, которые зависят от этой системы координат, обозначаются штрихами, например, x' , y' , a' .

Вектор от начала инерциальной системы отсчета до начала ускоренной системы отсчета обычно обозначается как R . Учитывая точку интереса, которая существует в обоих кадрах, вектор от инерциального начала координат до точки называется r , а вектор от ускоренного начала координат до точки называется r ′ .

Из геометрии ситуации

$\mathbf {r} =\mathbf {R} +\mathbf {r} '.$

Взяв первую и вторую производные от этого по времени

$\mathbf {v} =\mathbf {V} +\mathbf {v} ',$

$\mathbf {a} =\mathbf {A} +\mathbf {a} '.$

где V и A — скорость и ускорение ускоренной системы относительно инерциальной системы, а v и a — скорость и ускорение интересующей точки относительно инерциальной системы отсчета.

Эти уравнения допускают преобразования между двумя системами координат; например, второй закон Ньютона можно записать как

$\mathbf {F} =m\mathbf {a} =m\mathbf {A} +m\mathbf {a} '.$

Когда происходит ускоренное движение из-за приложенной силы, проявляется инерция. Если электромобиль, предназначенный для подзарядки своей аккумуляторной системы, при замедлении переключается на торможение, аккумуляторы перезаряжаются, иллюстрируя физическую силу проявления инерции. Однако проявление инерции не предотвращает ускорение (или замедление), поскольку проявление инерции происходит в ответ на изменение скорости под действием силы. Если смотреть с точки зрения вращающейся системы отсчета, проявление инерции, по-видимому, оказывает силу (либо в центробежном направлении, либо в направлении, ортогональном движению объекта, эффект Кориолиса ).

Распространенным видом ускоренной системы отсчета является кадр, который одновременно вращается и перемещается (примером является система отсчета, прикрепленная к компакт-диску, который воспроизводится, пока плеер находится в руках).

Такое расположение приводит к уравнению (вывод см. Фиктивная сила в разделе « »):

$\mathbf {a} =\mathbf {a} '+{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '+2{\boldsymbol {\omega }}\times \mathbf {v} '+{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')+\mathbf {A} _{0},$

или, чтобы найти ускорение в ускоренной системе отсчета,

$\mathbf {a} '=\mathbf {a} -{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '-2{\boldsymbol {\omega }}\times \mathbf {v} '-{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')-\mathbf {A} _{0}.$

Умножение на массу m дает

$\mathbf {F} '=\mathbf {F} _{\mathrm {physical} }+\mathbf {F} '_{\mathrm {Euler} }+\mathbf {F} '_{\mathrm {Coriolis} }+\mathbf {F} '_{\mathrm {centripetal} }-m\mathbf {A} _{0},$

где

$\mathbf {F} '_{\mathrm {Euler} }=-m{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '$ ( сила Эйлера ),

$\mathbf {F} '_{\mathrm {Coriolis} }=-2m{\boldsymbol {\omega }}\times \mathbf {v} '$ ( сила Кориолиса ),

$\mathbf {F} '_{\mathrm {centrifugal} }=-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')=m(\omega ^{2}\mathbf {r} '-({\boldsymbol {\omega }}\cdot \mathbf {r} '){\boldsymbol {\omega }})$ ( центробежная сила ).

Отделение неинерциальной от инерциальной системы отсчета

Теория

Основная статья: Фиктивная сила

См. также: Неинерциальная система отсчета , Вращающиеся сферы и Аргумент ковша.

Рисунок 2 : Две сферы, связанные веревкой и вращающиеся с угловой скоростью ω. Из-за вращения нить, связывающая сферы вместе, находится под натяжением.

Рисунок 3 : Покомпонентный вид вращающихся сфер в инерциальной системе отсчета, показывающий центростремительные силы на сферах, создаваемые натяжением связывающей веревки.

Инерциальные и неинерциальные системы отсчета можно отличить по отсутствию или наличию фиктивных сил .

Результатом этого пребывания в неинерциальной системе отсчета является требование от наблюдателя ввести в свои расчеты фиктивную силу…

- Сидни Боровиц и Лоуренс А. Борнштейн в «Современном взгляде на элементарную физику» , с. 138

Наличие фиктивных сил указывает на то, что физические законы не являются самыми простыми доступными законами, с точки зрения специального принципа относительности система, в которой присутствуют фиктивные силы, не является инерциальной системой отсчета:

Уравнения движения в неинерциальной системе отличаются от уравнений инерциальной системы дополнительными членами, называемыми силами инерции. Это позволяет экспериментально обнаружить неинерциальную природу системы.

- В. И. Арнольд : Математические методы классической механики , второе издание, с. 129

На тела в неинерциальных системах отсчета действуют так называемые фиктивные силы (псевдосилы); то есть силы , возникающие в результате ускорения самой системы отсчета , а не какой-либо физической силы, действующей на тело. Примерами фиктивных сил являются центробежная сила и сила Кориолиса во вращающихся системах отсчета .

Чтобы применить ньютоновское определение инерциальной системы отсчета, необходимо прояснить понимание разделения между «фиктивными» и «реальными» силами.

Например, рассмотрим неподвижный объект в инерциальной системе отсчета. В состоянии покоя чистая сила не применяется. Но в системе координат, вращающейся вокруг фиксированной оси, кажется, что объект движется по кругу и подвергается действию центростремительной силы. Как можно решить, что вращающаяся система отсчета является неинерциальной? Есть два подхода к этому решению: один подход заключается в поиске происхождения фиктивных сил (силы Кориолиса и центробежной силы). Выяснится, что у этих сил нет ни источников, ни связанных с ними носителей силы , ни порождающих тел. Второй подход заключается в рассмотрении различных систем отсчета. Для любой инерциальной системы отсчета сила Кориолиса и центробежная сила исчезают, поэтому применение принципа специальной теории относительности идентифицирует эти системы, в которых силы исчезают, как подчиняющиеся одним и тем же самым простым физическим законам, и, следовательно, постановит, что вращающаяся система отсчета не является инерционная рамка.

Ньютон сам исследовал эту проблему, используя вращающиеся сферы, как показано на рисунках 2 и 3. Он отметил, что, если сферы не вращаются, натяжение связывающей веревки измеряется как ноль в каждой системе отсчета. Если кажется, что сферы только вращаются (то есть мы наблюдаем за неподвижными сферами из вращающейся системы отсчета), нулевое натяжение струны объясняется наблюдением, что центростремительная сила создается сочетанием центробежной силы и сил Кориолиса, поэтому нет напряжение необходимо. Если сферы действительно вращаются, наблюдаемое напряжение в точности соответствует центростремительной силе, необходимой для кругового движения. Таким образом, измерение натяжения струны определяет инерционную систему отсчета: это та, в которой натяжение струны обеспечивает именно ту центростремительную силу, которая требуется для движения, как она наблюдается в этой системе отсчета, а не другое значение. То есть инерциальная система отсчета — это та, в которой фиктивные силы исчезают.

Что касается линейного ускорения , Ньютон выразил общую идею необнаружимости прямолинейных ускорений:

Если тела, как бы они ни двигались между собой, подталкиваются в направлении параллельных линий равными ускоряющими силами, они будут продолжать двигаться между собой таким же образом, как если бы их не подталкивала никакая такая сила.

- Исаак Ньютон: Следствие принципов VI, с. 89, в переводе Эндрю Мотта

Этот принцип обобщает понятие инерциальной системы отсчета. Например, наблюдатель, находящийся в свободно падающем лифте, будет утверждать, что он сам является действительной инерциальной системой отсчета, даже если он ускоряется под действием силы тяжести, пока у него нет знаний ни о чем за пределами лифта. Итак, строго говоря, инерциальная система отсчета – понятие относительное. Имея это в виду, инерциальные системы отсчета можно в совокупности определить как набор систем, которые являются стационарными или движущимися с постоянной скоростью относительно друг друга, так что одна инерциальная система отсчета определяется как элемент этого набора.

Чтобы эти идеи были применимы, все, что наблюдается в кадре, должно подчиняться базовому общему ускорению, разделяемому самим кадром. Эта ситуация применима, например, к примеру с лифтом, где все объекты подвергаются одинаковому гравитационному ускорению, а сам лифт ускоряется с одинаковой скоростью.

Приложения

Инерциальные навигационные системы использовали группу гироскопов и акселерометров для определения ускорений относительно инерциального пространства. После того, как гироскоп раскрутился в определенной ориентации в инерциальном пространстве, закон сохранения углового момента требует, чтобы он сохранял эту ориентацию до тех пор, пока к нему не прикладываются внешние силы. Три ортогональных гироскопа устанавливают инерциальную систему отсчета, а ускорители измеряют ускорение относительно этой системы. Затем ускорения вместе с часами можно использовать для расчета изменения положения. Таким образом, инерциальная навигация представляет собой форму точного счисления , которая не требует внешнего воздействия и, следовательно, не может быть подавлена ​​каким-либо внешним или внутренним источником сигнала.

Гирокомпас . , используемый для навигации морских судов, находит геометрический север Он делает это не за счет измерения магнитного поля Земли, а за счет использования инерциального пространства в качестве ориентира. Внешний корпус гирокомпасного устройства удерживается таким образом, чтобы оставаться на одной линии с местным отвесом. Когда колесо гироскопа внутри устройства гирокомпаса раскручивается, способ подвешивания колеса гироскопа заставляет колесо гироскопа постепенно выравнивать свою ось вращения с осью Земли. Выравнивание по оси Земли - единственное направление, в котором ось вращения гироскопа может быть стационарной по отношению к Земле и не требовать изменения направления по отношению к инерциальному пространству. После раскрутки гирокомпас может достичь направления, совмещенного с земной осью, всего за четверть часа.

См. также

• Абсолютное вращение
• Диффеоморфизм
• Галилеева инвариантность
• Общая ковариация
• Локальная система отсчета
• Лоренц-ковариация
• первый закон Ньютона
• Квантовая система отсчета

Дальнейшее чтение

• Эдвин Ф. Тейлор и Джон Арчибальд Уилер , Физика пространства-времени , 2-е изд. (Фриман, Нью-Йорк, 1992 г.)
• Альберт Эйнштейн , Относительность, специальная и общая теории , 15-е изд. (1954)
• Пуанкаре, Анри (1900). «Теория Лоренца и принцип реакции». Голландские архивы . В : 253–78.
• Альберт Эйнштейн , «Об электродинамике движущихся тел» , включенный в «Принцип относительности» , стр. 38. Дувр, 1923 г.

Вращение Вселенной

• Джулиан Б. Барбур; Герберт Пфистер (1998). Принцип Маха: от ведра Ньютона к квантовой гравитации . Биркхойзер. п. 445. ИСБН  0-8176-3823-7 .
• П. Дж. Нахин (1999). Машины времени . Спрингер. п. 369; Сноска 12.ISBN  0-387-98571-9 .
• Б. Чобану, И. Радинчи. Архивировано 19 июля 2013 г. в Wayback Machine. Моделирование электрических и магнитных полей во вращающейся вселенной Рим. Путешествие. Физ., Том. 53, № 1–2, стр. 405–415, Бухарест, 2008 г.
• Юрий Н. Обухов, Торальф Хробок, Майк Шерфнер. Архивировано 9 июля 2017 года в Wayback Machine. Вращающаяся инфляция без сдвига, Phys. Ред. Д 66, 043518 (2002) [5 страниц]
• Юрий Н. Обухов О физических основах и наблюдательных эффектах космического вращения (2000)
• Ли-Синь Ли. Архивировано 9 июля 2017 года в Wayback Machine. Влияние глобального вращения Вселенной на формирование галактик. Общая теория относительности и гравитации, 30 (1998). два : 10.1023/A:1018867011142
• П. Берч. Архивировано 5 марта 2016 г. в Wayback Machine. Вращается ли Вселенная? Природа 298, 451–454 (29 июля 1982 г.)
• Курт Гёдель Пример нового типа космологических решений уравнений поля гравитации Эйнштейна Rev. Mod. Физ., Том. 21, с. 447, 1949.

Внешние ссылки

• Запись в Стэнфордской энциклопедии философии. Архивировано 4 декабря 2010 года в Wayback Machine.
• Анимационный клип на YouTube, показывающий сцены, рассматриваемые как с инерциальной, так и с вращающейся системы отсчета, визуализируя Кориолис и центробежные силы.
• «Является ли гравитация иллюзией?» . PBS «Пространство-время» . 3 июня 2015 г. Архивировано из оригинала 13 ноября 2021 г. – на YouTube .