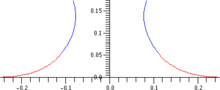
Уравнение Юнга – Лапласа

В физике уравнение Юнга-Лапласа ( / l ə ˈ p l ɑː s / ) представляет собой алгебраическое уравнение, которое описывает разницу капиллярного давления, поддерживаемую на границе раздела двух статических жидкостей , таких как вода и воздух , из-за явления поверхностного натяжение или натяжение стены , хотя использование последнего применимо только в том случае, если предположить, что стена очень тонкая. Уравнение Юнга-Лапласа связывает разницу давлений с формой поверхности или стенки и имеет фундаментальное значение при исследовании статических капиллярных поверхностей . Это формулировка нормального баланса напряжений для статических жидкостей, встречающихся на границе раздела, где граница раздела рассматривается как поверхность ( нулевая толщина): ${\begin{aligned}\Delta p&=-\gamma \nabla \cdot {\hat {n}}\\&=-2\gamma H_{f}\\&=-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)\end{aligned}}$ где $\Delta p$ — давление Лапласа , разность давлений на границе раздела жидкости (внешнее давление минус внутреннее давление), $\gamma$ поверхностное натяжение (или пристеночное натяжение ), ${\hat {n}}$ - единичная нормаль, направленная наружу от поверхности, $H_{f}$ – средняя кривизна , а $R_{1}$ и $R_{2}$ являются главными радиусами кривизны . Обратите внимание, что рассматривается только нормальное напряжение, поскольку статический интерфейс возможен только при отсутствии касательного напряжения. ^{[ 1 ]}

Уравнение названо в честь Томаса Янга , разработавшего качественную теорию поверхностного натяжения в 1805 году, и Пьера-Симона Лапласа, завершившего математическое описание в следующем году. Иногда его также называют уравнением Юнга-Лапласа-Гаусса, поскольку Карл Фридрих Гаусс объединил работы Юнга и Лапласа в 1830 году, выведя как дифференциальное уравнение, так и граничные условия, используя Иоганна Бернулли . виртуальной работы принципы ^{[ 2 ]}

Мыльные пленки

Если разница давлений равна нулю, как в мыльной пленке без гравитации, граница раздела примет форму минимальной поверхности .

Эмульсии

Уравнение также объясняет энергию, необходимую для создания эмульсии . Чтобы сформировать маленькие, сильно изогнутые капли эмульсии, требуется дополнительная энергия для преодоления большого давления, возникающего в результате их небольшого радиуса.

Давление Лапласа, которое выше для капель меньшего размера, вызывает диффузию молекул из самых маленьких капель в эмульсии и приводит к огрублению эмульсии за счет созревания Оствальда . ^{[ нужна ссылка ]}

Капиллярное давление в трубке

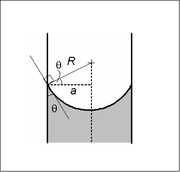
В достаточно узкой (т. е. с низким числом Бонда ) трубке круглого сечения (радиус а ) граница раздела двух жидкостей образует мениск , представляющий собой участок поверхности сферы R. радиуса Скачок давления на этой поверхности связан с радиусом и поверхностным натяжением γ соотношением $\Delta p={\frac {2\gamma }{R}}.$

Это можно показать, записав уравнение Юнга – Лапласа в сферической форме с граничным условием угла контакта , а также заданным граничным условием по высоте, скажем, на дне мениска. Решение представляет собой часть сферы, и решение будет существовать только для разности давлений, показанной выше. Это важно, поскольку не существует другого уравнения или закона, определяющего разницу давления; существование решения для одного конкретного значения перепада давлений предписывает это.

Радиус сферы будет функцией только угла контакта θ, который, в свою очередь, зависит от точных свойств жидкостей и материала контейнера, с которым рассматриваемые жидкости контактируют/взаимодействуют: $R={\frac {a}{\cos \theta }}$

так что разницу давлений можно записать как: $\Delta p={\frac {2\gamma \cos \theta }{a}}.$

Иллюстрация капиллярного подъема. Красный = угол контакта менее 90°; синий = угол контакта более 90°

Для поддержания гидростатического равновесия индуцированное капиллярное давление уравновешивается изменением высоты h , которое может быть положительным или отрицательным, в зависимости от того, меньше или больше 90° угол смачивания. Для жидкости плотностью ρ: $\rho gh={\frac {2\gamma \cos \theta }{a}}.$ где g — ускорение свободного падения . Иногда это называют законом Юрина или высотой Юрина. ^{[ 3 ]} в честь Джеймса Джурина, изучавшего этот эффект в 1718 году. ^{[ 4 ]}

Для стеклянной трубки, наполненной водой, в воздухе на уровне моря :

γ = 0,0728 Дж/м ² и 20° С
θ = 20° (0,35 рад )
ρ = 1000 кг/м ³
г = 9,8 м/с ²

и поэтому высота столба воды определяется выражением: $h\approx {{1.4\times 10^{-5}}\mathrm {m} ^{2} \over a}.$ Таким образом, для трубки шириной 2 мм (радиусом 1 мм) вода поднимется на 14 мм. Однако для капилляра радиусом 0,1 мм вода поднимется на 14 см (около 6 дюймов ).

Капиллярное действие в целом

В общем случае для свободной поверхности и при приложении «избыточного давления» Δ p на границе раздела в равновесии существует баланс между приложенным давлением, гидростатическим давлением и эффектами поверхностного натяжения. Уравнение Юнга – Лапласа принимает вид: $\Delta p=\rho gh-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)$

Уравнение можно обезразмерить с точки зрения его характерного масштаба длины, длины капилляра : $L_{c}={\sqrt {\frac {\gamma }{\rho g}}},$ и характеристическое давление $p_{c}={\frac {\gamma }{L_{c}}}={\sqrt {\gamma \rho g}}.$

Для чистой воды при стандартной температуре и давлении длина капилляра составляет ~2 мм .

Тогда безразмерное уравнение принимает вид: $h^{*}-\Delta p^{*}=\left({\frac {1}{{R_{1}}^{*}}}+{\frac {1}{{R_{2}}^{*}}}\right).$

Таким образом, форма поверхности определяется только одним параметром — избыточным давлением жидкости Δ p ^* а масштаб поверхности определяется длиной капилляра . Решение уравнения требует начального условия положения и градиента поверхности в начальной точке.

Висячая капля образуется при избыточном давлении Δp. ^*=3 и начальное условие r ₀ =10 ⁻⁴, z ₀ =0, dz / dr =0

Жидкостный мостик создается при избыточном давлении Δp. ^*=3,5 и начальное условие r ₀ =0,25 ⁻⁴, z ₀ =0, dz / dr =0

Осесимметричные уравнения

(Безразмерную) форму r ( z ) осесимметричной поверхности можно найти, подставив общие выражения для главных кривизн в гидростатические уравнения Юнга – Лапласа : ^{[ 5 ]} ${\frac {r''}{(1+r'^{2})^{{3}/{2}}}}-{\frac {1}{r(z){\sqrt {1+r'^{2}}}}}=z-\Delta p^{*}$ ${\frac {z''}{(1+z'^{2})^{3/2}}}+{\frac {z'}{r(1+z'^{2})^{{1}/{2}}}}=\Delta p^{*}-z(r).$

Применение в медицине

В медицине его часто называют законом Лапласа , используемым в контексте сердечно-сосудистой физиологии . ^{[ 6 ]} а также физиология дыхания , хотя последнее использование часто ошибочно. ^{[ 7 ]}

История

Фрэнсис Хоксби выполнил некоторые из самых ранних наблюдений и экспериментов в 1709 году. ^{[ 8 ]} и это было повторено в 1718 году Джеймсом Джурином , который заметил, что высота жидкости в капиллярной колонне зависит только от площади поперечного сечения на поверхности, а не от каких-либо других размеров колонны. ^{[ 4 ]}^{[ 9 ]}

Томас Янг заложил основы уравнения в своей статье 1804 года « Очерк сцепления жидкостей». ^{[ 10 ]} где он в описательных терминах изложил принципы, регулирующие контакт между жидкостями (наряду со многими другими аспектами поведения жидкостей). Пьер Симон Лаплас продолжил это в «Небесной механике». ^{[ 11 ]} с приведенным выше формальным математическим описанием, которое в символических терминах воспроизводило отношения, описанные ранее Янгом.

Лаплас принял идею, выдвинутую Хоксби в его книге «Физико-механические эксперименты» (1709 г.), о том, что это явление возникает из-за силы притяжения, неощутимой на ощутимых расстояниях. ^{[ 12 ]}^{[ 13 ]} Часть, которая касается действия твердого тела на жидкость и взаимного действия двух жидкостей, не была тщательно разработана, но в конечном итоге была завершена Карлом Фридрихом Гауссом . ^{[ 14 ]} Франц Эрнст Нойман (1798–1895) позже внес некоторые подробности. ^{[ 15 ]}^{[ 9 ]}^{[ 16 ]}

Ссылки

^ Модуль поверхностного натяжения. Архивировано 27 октября 2007 г. в Wayback Machine , Джоном У.М. Бушем, в MIT OCW .
^ Роберт Финн (1999). «Капиллярные поверхностные интерфейсы» (PDF) . АМС .
^ «Правило Юрина» . Словарь научно-технических терминов МакГроу-Хилла . МакГроу-Хилл на Answers.com. 2003 . Проверено 5 сентября 2007 г.
^ Jump up to: ^а ^б
Видеть:
- Джеймс Джурин (1718 г.) «Отчет о некоторых экспериментах, показанных перед Королевским обществом; с исследованием причин некоторого подъема и взвешивания воды в капиллярных трубках», Philosophical Transactions of the Royal Society of London , 30 : 739– 747.
- Джеймс Джурин (1719) «Отчет о некоторых новых экспериментах, касающихся воздействия стеклянных трубок на воду и ртуть», Philosophical Transactions of the Royal Society of London , 30 : 1083–1096.
^ Лэмб, Х. Статика, включая гидростатику и элементы теории упругости, 3-е изд. Кембридж, Англия: Издательство Кембриджского университета, 1928.
^ Басфорд, Джеффри Р. (2002). «Закон Лапласа и его значение для современной медицины и реабилитации». Архив физической медицины и реабилитации . 83 (8): 1165–1170. дои : 10.1053/апмр.2002.33985 . ПМИД 12161841 .
^ Прейндж, Генри Д. (2003). «Закон Лапласа и альвеолы: неправильное представление об анатомии и неправильное применение физики». Достижения в области физиологического образования . 27 (1): 34–40. дои : 10.1152/advan.00024.2002 . ПМИД 12594072 . S2CID 7791096 .
^
См.:
- Фрэнсис Хоксби, Физико-механические эксперименты на различных предметах ... (Лондон, Англия: (самоиздание автора; напечатано Р. Бругисом), 1709), стр. 139–1.
- Фрэнсис Хоксби (1711 г.) «Отчет об эксперименте, касающемся направления капли апельсинового масла между двумя стеклянными плоскостями, к любой из их сторон, которая ближе всего прижата друг к другу», «Философские труды Лондонского королевского общества» , 27 : 374–375.
- Фрэнсис Хоксби (1712 г.) «Отчет об эксперименте по подъему воды между двумя стеклянными плоскостями в гиперболической фигуре», Philosophical Transactions of the Royal Society of London , 27 : 539–540.
^ Jump up to: ^а ^б Максвелл, Джеймс Клерк ; Стратт, Джон Уильям (1911). «Капиллярное действие» . Британская энциклопедия . Том. 5 (11-е изд.). стр. 256–275.
^ Томас Янг (1805) «Очерк о сцеплении жидкостей», Philosophical Transactions of the Royal Society of London , 95 : 65–87.
^ Пьер Симон, маркиз де Лаплас, Traité de Mécanique Céleste , том 4, (Париж, Франция: Courcier, 1805), Дополнение к десятой книге Traité de Mécanique Céleste , страницы 1–79 .
^ Пьер Симон, маркиз де Лаплас, Traité de Mécanique Céleste , том 4, (Париж, Франция: Courcier, 1805), Дополнение к десятой книге Traité de Mécanique Céleste . На странице 2 Приложения Лаплас утверждает, что капиллярное действие обусловлено «… законами, согласно которым притяжение чувствительно [значительно] только на неощутимых [бесконечно малых] расстояниях…).
^ В 1751 году Иоганн Андреас Зегнер пришел к тому же выводу, к которому пришел Хоксби в 1709 году: Дж. А. фон Зегнер (1751) « О формах жидких поверхностей», Commentarii Societatis Regiae Scientiarum Gottingensis (Мемуары Королевского научного общества Геттингена). ), 1 : 301–372. На странице 303 Сегнер предполагает, что жидкости удерживаются вместе силой притяжения ( vim attractricem ), действующей на таких коротких расстояниях, «что никто еще не мог воспринять ее своими органами чувств» (... ut nullo adhuc sensu percipi poterit. ) .
^ Карл Фридрих Гаусс, Общие принципы теории жидких форм в состоянии равновесия (Геттинген, (Германия): Дитерихс, 1830). Доступно онлайн по адресу: Hathi Trust.
^ Франц Нейман с А. Вангерином, изд., Лекции по теории капиллярности (Лейпциг, Германия: Б. Г. Тойбнер, 1894).
^ Rouse Ball, WW [1908] (2003) « Пьер Симон Лаплас (1749–1827) », в «Кратком обзоре истории математики» , 4-е изд., Дувр, ISBN 0-486-20630-0

Дальнейшее чтение

Максвелл, Джеймс Клерк ; Стратт, Джон Уильям (1911). «Капиллярное действие» . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 5 (11-е изд.). Издательство Кембриджского университета. стр. 256–275.
Бэтчелор, Г.К. (1967) Введение в гидродинамику , издательство Кембриджского университета
Юрин, Дж. (1716). «Отчет о некоторых экспериментах, показанных Королевскому обществу; с исследованием причины подъема и взвешивания воды в капиллярных трубках» . Философские труды Королевского общества . 30 (351–363): 739–747. дои : 10.1098/rstl.1717.0026 . S2CID 186211806 .
Тадрос Т.Ф. (1995) Поверхностно-активные вещества в агрохимикатах , серия Surfactant Science, том 54, Dekker

[1] Модуль поверхностного натяжения. Архивировано 27 октября 2007 г. в Wayback Machine , Джоном У.М. Бушем, в MIT OCW .

[2] Роберт Финн (1999). «Капиллярные поверхностные интерфейсы» (PDF) . АМС .

[3] «Правило Юрина» . Словарь научно-технических терминов МакГроу-Хилла . МакГроу-Хилл на Answers.com. 2003 . Проверено 5 сентября 2007 г.

[jurin-4] Jump up to: ^а ^б Видеть:
Джеймс Джурин (1718 г.) «Отчет о некоторых экспериментах, показанных перед Королевским обществом; с исследованием причин некоторого подъема и взвешивания воды в капиллярных трубках», Philosophical Transactions of the Royal Society of London , 30 : 739– 747.

Джеймс Джурин (1719) «Отчет о некоторых новых экспериментах, касающихся воздействия стеклянных трубок на воду и ртуть», Philosophical Transactions of the Royal Society of London , 30 : 1083–1096.

[5] Джеймс Джурин (1718 г.) «Отчет о некоторых экспериментах, показанных перед Королевским обществом; с исследованием причин некоторого подъема и взвешивания воды в капиллярных трубках», Philosophical Transactions of the Royal Society of London , 30 : 739– 747.

[6] Джеймс Джурин (1719) «Отчет о некоторых новых экспериментах, касающихся воздействия стеклянных трубок на воду и ртуть», Philosophical Transactions of the Royal Society of London , 30 : 1083–1096.

[5] Лэмб, Х. Статика, включая гидростатику и элементы теории упругости, 3-е изд. Кембридж, Англия: Издательство Кембриджского университета, 1928.

[6] Басфорд, Джеффри Р. (2002). «Закон Лапласа и его значение для современной медицины и реабилитации». Архив физической медицины и реабилитации . 83 (8): 1165–1170. дои : 10.1053/апмр.2002.33985 . ПМИД 12161841 .

[7] Прейндж, Генри Д. (2003). «Закон Лапласа и альвеолы: неправильное представление об анатомии и неправильное применение физики». Достижения в области физиологического образования . 27 (1): 34–40. дои : 10.1152/advan.00024.2002 . ПМИД 12594072 . S2CID 7791096 .

[8] См.:
Фрэнсис Хоксби, Физико-механические эксперименты на различных предметах ... (Лондон, Англия: (самоиздание автора; напечатано Р. Бругисом), 1709), стр. 139–1.

Фрэнсис Хоксби (1711 г.) «Отчет об эксперименте, касающемся направления капли апельсинового масла между двумя стеклянными плоскостями, к любой из их сторон, которая ближе всего прижата друг к другу», «Философские труды Лондонского королевского общества» , 27 : 374–375.

Фрэнсис Хоксби (1712 г.) «Отчет об эксперименте по подъему воды между двумя стеклянными плоскостями в гиперболической фигуре», Philosophical Transactions of the Royal Society of London , 27 : 539–540.

[11] Фрэнсис Хоксби, Физико-механические эксперименты на различных предметах ... (Лондон, Англия: (самоиздание автора; напечатано Р. Бругисом), 1709), стр. 139–1.

[12] Фрэнсис Хоксби (1711 г.) «Отчет об эксперименте, касающемся направления капли апельсинового масла между двумя стеклянными плоскостями, к любой из их сторон, которая ближе всего прижата друг к другу», «Философские труды Лондонского королевского общества» , 27 : 374–375.

[13] Фрэнсис Хоксби (1712 г.) «Отчет об эксперименте по подъему воды между двумя стеклянными плоскостями в гиперболической фигуре», Philosophical Transactions of the Royal Society of London , 27 : 539–540.

[ebca-9] Jump up to: ^а ^б Максвелл, Джеймс Клерк ; Стратт, Джон Уильям (1911). «Капиллярное действие» . Британская энциклопедия . Том. 5 (11-е изд.). стр. 256–275.

[10] Томас Янг (1805) «Очерк о сцеплении жидкостей», Philosophical Transactions of the Royal Society of London , 95 : 65–87.

[11] Пьер Симон, маркиз де Лаплас, Traité de Mécanique Céleste , том 4, (Париж, Франция: Courcier, 1805), Дополнение к десятой книге Traité de Mécanique Céleste , страницы 1–79 .

[12] Пьер Симон, маркиз де Лаплас, Traité de Mécanique Céleste , том 4, (Париж, Франция: Courcier, 1805), Дополнение к десятой книге Traité de Mécanique Céleste . На странице 2 Приложения Лаплас утверждает, что капиллярное действие обусловлено «… законами, согласно которым притяжение чувствительно [значительно] только на неощутимых [бесконечно малых] расстояниях…).

[13] В 1751 году Иоганн Андреас Зегнер пришел к тому же выводу, к которому пришел Хоксби в 1709 году: Дж. А. фон Зегнер (1751) « О формах жидких поверхностей», Commentarii Societatis Regiae Scientiarum Gottingensis (Мемуары Королевского научного общества Геттингена). ), 1 : 301–372. На странице 303 Сегнер предполагает, что жидкости удерживаются вместе силой притяжения ( vim attractricem ), действующей на таких коротких расстояниях, «что никто еще не мог воспринять ее своими органами чувств» (... ut nullo adhuc sensu percipi poterit. ) .

[14] Карл Фридрих Гаусс, Общие принципы теории жидких форм в состоянии равновесия (Геттинген, (Германия): Дитерихс, 1830). Доступно онлайн по адресу: Hathi Trust.

[15] Франц Нейман с А. Вангерином, изд., Лекции по теории капиллярности (Лейпциг, Германия: Б. Г. Тойбнер, 1894).

[16] Rouse Ball, WW [1908] (2003) « Пьер Симон Лаплас (1749–1827) », в «Кратком обзоре истории математики» , 4-е изд., Дувр, ISBN 0-486-20630-0

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]