Материал Максвелла

Материал Максвелла — простейшая модель вязкоупругого материала, проявляющая свойства типичной жидкости. Он демонстрирует вязкое течение в длительном масштабе времени, но дополнительное упругое сопротивление быстрым деформациям. Он назван в честь Джеймса Клерка Максвелла , который предложил эту модель в 1867 году. Она также известна как жидкость Максвелла. Обобщение скалярной связи на тензорное уравнение лишено мотивации со стороны более микроскопических моделей и не соответствует концепции материальной объективности. Однако этому критерию соответствует модель Максвелла с верхней конвекцией .

Определение

Схема материала Максвелла

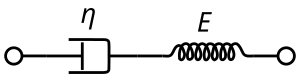
Модель Максвелла представлена ​​чисто вязкостным демпфером и чисто упругой пружиной, соединенными последовательно. как показано на схеме. Если вместо этого мы соединим эти два элемента параллельно, мы получаем обобщенную модель твердого материала Кельвина–Фойгта .

В конфигурации Максвелла при приложенном осевом напряжении полное напряжение $\sigma _{\mathrm {Total} }$ и общая деформация, $\varepsilon _{\mathrm {Total} }$ можно определить следующим образом:

$\sigma _{\mathrm {Total} }=\sigma _{\rm {D}}=\sigma _{\rm {S}}$

$\varepsilon _{\mathrm {Total} }=\varepsilon _{\rm {D}}+\varepsilon _{\rm {S}}$

где индекс D обозначает напряжение-деформацию в демпфере, а индекс S указывает напряжение-деформацию в пружине. Взяв производную деформации по времени, получим:

${\frac {d\varepsilon _{\mathrm {Total} }}{dt}}={\frac {d\varepsilon _{\rm {D}}}{dt}}+{\frac {d\varepsilon _{\rm {S}}}{dt}}={\frac {\sigma }{\eta }}+{\frac {1}{E}}{\frac {d\sigma }{dt}}$

где E — модуль упругости, а η — коэффициент вязкости материала. Эта модель описывает демпфер как ньютоновскую жидкость и моделирует пружину по закону Гука .

В материале Максвелла напряжение σ , деформация ε и скорость их изменения во времени t определяются уравнениями вида:

${\frac {1}{E}}{\frac {d\sigma }{dt}}+{\frac {\sigma }{\eta }}={\frac {d\varepsilon }{dt}}$

или, в точечной записи:

${\frac {\dot {\sigma }}{E}}+{\frac {\sigma }{\eta }}={\dot {\varepsilon }}$

Уравнение можно применить либо к напряжению сдвига , либо к равномерному растяжению материала. В первом случае вязкость соответствует вязкости ньютоновской жидкости . В последнем случае оно имеет несколько иное значение, касающееся напряжения и скорости деформации.

Модель обычно применяется к случаю малых деформаций. Для больших деформаций следует учитывать некоторую геометрическую нелинейность. Самый простой способ обобщения модели Максвелла можно найти в модели Максвелла с верхней конвекцией .

Эффект внезапной деформации

Зависимость безразмерного напряжения от безразмерного времени при постоянной деформации

Если материал Максвелла внезапно деформируется и удерживается напряжением под $\varepsilon _{0}$, то напряжение затухает в характерном временном масштабе ${\frac {\eta }{E}}$, известное как время релаксации . Это явление известно как релаксация стресса .

На рисунке представлена ​​зависимость безразмерного напряжения ${\frac {\sigma (t)}{E\varepsilon _{0}}}$ в безразмерное время ${\frac {E}{\eta }}t$:

Если мы освободим материал вовремя $t_{1}$, то упругий элемент отпружинит на величину

$\varepsilon _{\mathrm {back} }=-{\frac {\sigma (t_{1})}{E}}=\varepsilon _{0}\exp \left(-{\frac {E}{\eta }}t_{1}\right).$

Поскольку вязкий элемент не вернется к своей первоначальной длине, необратимую составляющую деформации можно упростить до следующего выражения:

$\varepsilon _{\mathrm {irreversible} }=\varepsilon _{0}\left[1-\exp \left(-{\frac {E}{\eta }}t_{1}\right)\right].$

Последствия внезапного стресса

Если материал Максвелла внезапно подвергается напряжению $\sigma _{0}$, то упругий элемент внезапно деформируется, а вязкий элемент будет деформироваться с постоянной скоростью:

$\varepsilon (t)={\frac {\sigma _{0}}{E}}+t{\frac {\sigma _{0}}{\eta }}$

Если в какое-то время $t_{1}$ мы выпустили материал, то деформация упругого элемента будет пружинящей, а деформация вязкого элемента не изменится:

$\varepsilon _{\mathrm {reversible} }={\frac {\sigma _{0}}{E}},$

$\varepsilon _{\mathrm {irreversible} }=t_{1}{\frac {\sigma _{0}}{\eta }}.$

Модель Максвелла не демонстрирует ползучести , поскольку она моделирует деформацию как линейную функцию времени.

Если небольшое напряжение прикладывается в течение достаточно длительного времени, необратимые деформации становятся большими. Таким образом, материал Максвелла представляет собой разновидность жидкости.

Влияние постоянной скорости деформации

Если материал Максвелла подвергается постоянной скорости деформации ${\dot {\epsilon }}$затем напряжение возрастает, достигая постоянного значения

$\sigma =\eta {\dot {\varepsilon }}$

В общем

$\sigma (t)=\eta {\dot {\varepsilon }}(1-e^{-Et/\eta })$

Динамический модуль

Релаксационный спектр материала Максвелла

Комплексный динамический модуль материала Максвелла будет:

$E^{*}(\omega )={\frac {1}{1/E-i/(\omega \eta )}}={\frac {E\eta ^{2}\omega ^{2}+i\omega E^{2}\eta }{\eta ^{2}\omega ^{2}+E^{2}}}$

Таким образом, компонентами динамического модуля являются:

$E_{1}(\omega )={\frac {E\eta ^{2}\omega ^{2}}{\eta ^{2}\omega ^{2}+E^{2}}}={\frac {(\eta /E)^{2}\omega ^{2}}{(\eta /E)^{2}\omega ^{2}+1}}E={\frac {\tau ^{2}\omega ^{2}}{\tau ^{2}\omega ^{2}+1}}E$

и

$E_{2}(\omega )={\frac {\omega E^{2}\eta }{\eta ^{2}\omega ^{2}+E^{2}}}={\frac {(\eta /E)\omega }{(\eta /E)^{2}\omega ^{2}+1}}E={\frac {\tau \omega }{\tau ^{2}\omega ^{2}+1}}E$

На рисунке показан релаксационный спектр материала Максвелла. Постоянная времени релаксации равна $\tau \equiv \eta /E$.

Синяя кривая	безразмерный модуль упругости ${\frac {E_{1}}{E}}$
Розовая кривая	безразмерный модуль потерь ${\frac {E_{2}}{E}}$
Желтая кривая	безразмерная кажущаяся вязкость ${\frac {E_{2}}{\omega \eta }}$
ось X	безразмерная частота $\omega \tau$.

См. также

• Материал для гамбургеров
• Обобщенная модель Максвелла
• Материал Кельвина – Фойгта
• Модель Олдройд-Б
• Стандартная линейная твердотельная модель
• Модель Максвелла с верхней конвекцией