Резонансная ультразвуковая спектроскопия

Резонансная ультразвуковая спектроскопия ( РУС ) — лабораторный метод, используемый в геологии и материаловедении для измерения фундаментальных свойств материалов, в том числе упругости . Этот метод основан на том факте, что твердые объекты имеют собственные частоты , на которых они вибрируют при механическом возбуждении. Собственная частота зависит от упругости, размера и формы объекта — RUS использует это свойство твердых тел для определения тензора упругости материала. Большим преимуществом этого метода является то, что весь тензор упругости получается из одного кристаллического образца за одно быстрое измерение. На более низких или более общих частотах этот метод известен как спектроскопия акустического резонанса .

История

Интерес к упругим свойствам возник у философов 17-го века, но настоящая теория упругости, указывающая на то, что упругие константы материала могут быть получены путем измерения скорости звука в этом материале, была обобщена только двести лет спустя. В 1964 году Д.Б. Фрейзер и Р.С. ЛеКроу использовали решение, рассчитанное в 1880 году Г. Ламе и Х. Лэмбом, для решения прямой задачи, а затем графически инвертировали его, что, возможно, стало первым измерением RUS. Тем не менее, нам пришлось дождаться участия геофизического сообщества, заинтересованного в определении внутреннего строения Земли , для решения обратной задачи : в 1970 году три геофизика усовершенствовали предыдущий метод и ввели термин метод резонансных сфер (РСТ). Воодушевленный обнадеживающими результатами, достигнутыми с лунными образцами , один из них поручил одному из своих учеников расширить метод для использования с образцами кубической формы. Этот метод, ныне известный как метод резонанса прямоугольного параллелепипеда (RPR), был дополнительно расширен И. Оно в 1976 г. Наконец, в конце 1980-х гг. А. Мильори и Дж. Мейнард расширили пределы метода с точки зрения нагрузки и низкоуровневых электронных измерений, а вместе с В. Вишером компьютерные алгоритмы к их современному состоянию, вводя окончательный термин резонансная ультразвуковая спектроскопия (РУС).

Теория

Во-первых, необходимо решить задачу расчета собственных частот через размеры образца, массу и набор гипотетических упругих постоянных (прямая задача). Затем необходимо применить алгоритм нелинейной инверсии, чтобы найти упругие константы по измеренным собственным частотам ( обратная задача ).

Лагранжева минимизация

Все измерения RUS выполняются на образцах, являющихся свободными вибраторами. Поскольку полного аналитического решения свободных колебаний твердых тел не существует, приходится полагаться на приближения. Методы конечных элементов основаны на уравновешивании сил, приложенных к элементу дифференциального объема , с последующим расчетом его реакции. С другой стороны, методы минимизации энергии определяют минимальную энергию и, следовательно, равновесную конфигурацию объекта. Среди методов минимизации энергии лагранжева минимизация наиболее часто используется в анализе RUS из-за ее преимущества в скорости (на порядок меньше, чем методы конечных элементов).

Процедура начинается с объекта объемом V, ограниченного его свободной поверхностью S. Лагранжиан имеет вид

$L=\int _{V}(KE-PE)dV(1)$

где KE – кинетической энергии плотность

$KE={\frac {1}{2}}\sum _{i}\rho \omega ^{2}u_{i}^{2}(2)$

PE - потенциальной энергии плотность

$PE={\frac {1}{2}}\sum _{i,j,k,l}c_{i,j,k,l}{\frac {du_{i}}{dx_{j}}}{\frac {du_{k}}{dx_{l}}}(3)$

Рис. 1 : Компьютерные иллюстрации некоторых нормальных форм колебаний образца прямоугольного параллелепипеда.

Здесь, $u_{i}$ – i-я компонента вектора смещения , ω – угловая частота из гармонической временной зависимости, $c_{i,j,k,l}$ – компонента тензора упругой жесткости, ρ – плотность . Индексы i, j и т. д. относятся к декартовым направлениям координат.

Чтобы найти минимум лагранжиана, вычислите дифференциал L как функцию u, произвольного изменения u в V и на S. Это дает:

$\delta L=\int _{V}{\Bigl \{}\sum _{i}{\Bigl [}\rho \omega ^{2}u_{i}-\sum _{j,k,l}c_{i,j,k,l}{\frac {\delta ^{2}u_{k}}{\delta x_{j}\delta x_{l}}}{\Bigr ]}\delta u_{i}{\Bigr \}}dV-\int _{S}{\Bigl \{}\sum _{i}{\Bigl [}\sum _{j,k,l}{\vec {n}}c_{i,j,k,l}{\frac {\delta u_{k}}{\delta x_{l}}}{\Bigr ]}du_{i}{\Bigr \}}dS(4)$

Потому что $u_{i}$ произвольно в V и на S, оба члена в квадратных скобках должны быть равны нулю. Если первое слагаемое приравнять нулю, получим уравнение упругих волн . Второй член в квадратных скобках представляет собой выражение граничных условий свободной поверхности ; ${\vec {n}}$ — единичный вектор, нормаль к S. Для свободного тела (как мы его предполагаем) сумма последнего члена равна нулю, и его можно игнорировать.

Таким образом, набор $u_{i}$ удовлетворяющими ранее упомянутым условиям, являются те смещения, которые соответствуют ω, являющемуся частотой нормальной моды системы. Это говорит о том, что нормальные колебания объекта (рис. 1) можно рассчитать, применив вариационный метод (в нашем случае вариационный метод Рэлея-Ритца , поясняемый в следующем параграфе) для определения как частот нормальных мод, так и описания колебаний. физические колебания. По словам Вишера, получение обоих уравнений из основного лагранжиана — это «математическая случайность, которая могла произойти во время потери бдительности Мерфи ».

Вариационный метод Рэлея-Ритца

Реализация этого подхода требует расширения $u_{i}$ в наборе базисных функций, соответствующих геометрии тела, подставив это выражение в уравнение. (1) и сведение задачи к диагонализации матрицы размера N×N ( проблема собственных значений ). Стационарные точки лагранжиана находятся путем решения проблемы собственных значений, вытекающей из уравнения. (4), то есть

$\omega ^{2}Ea=\Gamma a(5)$

где an — приближения к движению, развернутые в полном базисном наборе, E происходит от члена кинетической энергии , а Γ — от члена упругой энергии . Порядок матриц составляет ~ 10 ^ 3 для хороших приближений.

Уравнение (5) определяет резонансные частоты по упругим модулям .

Обратная задача

Обратная задача вывода упругих констант из измеренного спектра механических резонансов не имеет аналитического решения , поэтому ее необходимо решать вычислительными методами. Для косвенного метода стартовый спектр резонансных частот $f_{n}^{cal}$ (n=1,2,...) рассчитывается с использованием расчетных значений упругих констант и известных размеров и плотности образца. Разница между расчетным и измеренным спектром резонансных частот, $f_{n}^{mea}$ (n=1,2,...) определяется количественно с помощью функции качества ,

$F=\sum _{n}w_{n}(f_{n}^{cal}-f_{n}^{mea})^{2}(6)$

где $w_{n}$ (n=1,2,...) — весовые коэффициенты, отражающие достоверность индивидуальных резонансных измерений. Затем ищут минимизацию функции F путем регрессии значений всех упругих констант с использованием компьютерного программного обеспечения, разработанного для этого процесса.

Измерения

Рис. 2 : Схема установки резонансной ультразвуковой спектроскопии с двумя преобразователями.

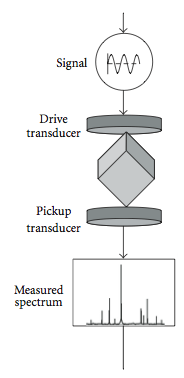
Наиболее распространенный метод обнаружения механического резонансного спектра показан на рис. 2, где небольшой образец в форме параллелепипеда слегка удерживается между двумя пьезоэлектрическими преобразователями . Один преобразователь используется для генерации упругой волны постоянной амплитуды и переменной частоты , тогда как другой используется для обнаружения резонанса образца. последовательность резонансных По мере качания частотного диапазона регистрируется пиков. Положение этих пиков происходит на собственных частотах $f_{n}$ (из которого определяются упругие константы) и добротность Q (мера того, насколько узок резонанс) дают информацию о диссипации упругой энергии .

В отличие от обычного ультразвукового измерения, в методе, который резонирует с образцом, не требуется сильная связь между преобразователем и образцом, поскольку образец ведет себя как естественный усилитель . Скорее, сохраняя как минимум пару между ними, вы получаете хорошее приближение к граничным условиям свободной поверхности и также стремитесь сохранить Q.При измерениях при переменной температуре образец удерживается между концами двух буферных стержней, которые соединяют образец с датчиками (рис. 3), поскольку датчики должны храниться при комнатной температуре . По давлению , наоборот, существует ограничение всего в несколько бар, поскольку применение более высоких давлений приводит к затуханию резонансов образца.

Образцы

RUS может применяться к широкому диапазону размеров образцов, от минимального порядка до нескольких сотен микрометров , но для измерения минеральной эластичности он используется для образцов размером обычно от 1 мм до 1 см.

Образцу, представляющему собой либо полностью плотный поликристаллический агрегат, либо монокристалл , придается правильная форма. Теоретически можно использовать образец любой формы, но вы получаете существенную экономию времени вычислений, используя резонаторы в форме прямоугольного параллелепипеда (RPR), сферические или цилиндрические (меньшая экономия времени при использовании цилиндров).

Рис. 3 : Образец сборки для измерения переменной температуры RUS.

Поскольку точность измерения строго зависит от точности подготовки образца, принимаются некоторые меры предосторожности: края RPR готовятся так, чтобы края были параллельны кристаллографическим направлениям; для цилиндров только ось может быть согласована с симметрией образца . RUS редко используется для образцов с более низкой симметрией, а для изотропных образцов выравнивание не имеет значения. Для более высоких симметрий удобно иметь края разной длины, чтобы предотвратить избыточный резонанс.

Измерения на монокристаллах требуют ориентации кристаллографических осей образца по краям ОПР, чтобы пренебречь вычислением ориентации и иметь дело только с упругими модулями .

Поликристаллические образцы в идеале должны быть полностью плотными, без трещин и без преимущественной ориентации зерен. Монокристаллические образцы не должны иметь внутренних дефектов, таких как двойные стенки . Поверхности всех образцов должны быть плоско отполированы, а противоположные грани должны быть параллельны. После подготовки плотность необходимо точно измерить, поскольку она масштабирует весь набор модулей упругости.

Датчики

РУС Ультразвуковые преобразователи предназначены для обеспечения сухого точечного контакта с образцом. Это связано с необходимостью наличия граничных условий на свободной поверхности для расчета упругих модулей по частотам. Для RPR это требует очень легкого прикосновения между углами образца и преобразователями. Углы используются потому, что они обеспечивают упруго слабую связь, снижая нагрузку, и потому, что они никогда не являются узловыми точками вибрации. Достаточно слабый контакт гарантирует, что коррекция трансдуции не потребуется.

Приложения

Являясь универсальным инструментом для характеристики упругих свойств твердых материалов, РУС нашел применение в самых разных областях.В науках о Земле одно из наиболее важных приложений связано с определением сейсмических скоростей в недрах Земли . В недавней работе например, упругие константы водного форстерита были измерены до 14,1 ГПа при температуре окружающей среды. Данное исследование показало, что агрегатные модули объема и сдвига водного форстерита увеличиваются с давлением с большей скоростью, чем соответствующие безводные фазы. Это означает, что в условиях окружающей среды VP и VS водного форстерита медленнее, чем безводного; и наоборот, с увеличением давления, а следовательно, и глубины, V _P и V _S водного форстерита превышают таковые у безводного. Кроме того, гидратация снижает соотношение V _P /V _S форстерита, максимальную волны сжатия азимутальную анизотропию и максимальное расщепление поперечной волны . Эти данные помогают нам определить состав мантии Земли и отличить области обогащения водородом от областей высокой температуры или частичного плавления.