Эквивалентная потенциальная температура

Эквивалентная потенциальная температура , обычно называемая тета-е $\left(\theta _{e}\right)$, — это величина, которая сохраняется при изменении давления воздушного потока (то есть при вертикальных движениях в атмосфере ), даже если водяной пар конденсируется во время этого изменения давления. Поэтому она более консервативна, чем обычная потенциальная температура , которая остается постоянной только при ненасыщенных вертикальных движениях (изменениях давления).

$\theta _{e}$ — это температура, которой достиг бы пакет с воздухом, если бы весь водяной пар в пакете конденсировался , высвобождая скрытое тепло , и пакет был адиабатически доведен до стандартного эталонного давления, обычно 1000 гПа (1000 мбар ), что примерно равно атмосферное давление на уровне моря .

Его использование для оценки стабильности атмосферы.

Стабильность несжимаемой жидкости

Подобно шару, балансирующему на вершине холма, более плотная жидкость, лежащая над менее плотной жидкостью, будет динамически нестабильной: опрокидывающие движения ( конвекция ) могут понизить центр тяжести и, таким образом, возникнут самопроизвольно, быстро создавая устойчивое расслоение, которое, таким образом, и является наблюдаемым. состояние практически всегда. Условием устойчивости несжимаемой жидкости является монотонное уменьшение плотности с высотой .

Стабильность сжимаемого воздуха: потенциальная температура

Если жидкость сжимаема , как воздух, критерием динамической устойчивости вместо этого является потенциальная плотность — плотность жидкости при фиксированном эталонном давлении. Для идеального газа (см. газовые законы ) критерием устойчивости столба воздуха является монотонное увеличение потенциальной температуры с высотой .

Чтобы понять это, рассмотрим сухую конвекцию в атмосфере, где вертикальные колебания давления значительны и важно адиабатическое изменение температуры: когда порция воздуха движется вверх, давление окружающей среды падает, заставляя эту порцию расширяться. Часть внутренней энергии посылки расходуется на выполнение работы, необходимой для расширения под действием атмосферного давления, поэтому температура посылки падает, хотя она и не потеряла тепла. И наоборот, тонущий пакет сжимается и становится теплее, хотя тепла не добавляется.

Воздух на вершине горы обычно холоднее, чем воздух в долине внизу, но такое расположение не нестабильно: если бы порция воздуха из долины каким-то образом была поднята на вершину горы, когда она достигла бы даже холоднее, чем уже находящийся там воздух, из-за адиабатического охлаждения; он будет тяжелее окружающего воздуха и опустится обратно в исходное положение. Точно так же, если бы порция холодного воздуха с вершины горы спустилась в долину, она оказалась бы теплее и легче, чем воздух долины, и поплыла бы обратно вверх по горе.

Таким образом, холодный воздух, лежащий поверх теплого, может быть стабильным, пока снижение температуры с высотой меньше адиабатического градиента ; динамически важной величиной является не температура, а потенциальная температура — температура, которую имел бы воздух, если бы его адиабатически довели до эталонного давления. Воздух вокруг горы стабилен, потому что воздух наверху из-за более низкого давления имеет более высокую потенциальную температуру, чем более теплый воздух внизу.

Эффекты конденсации воды: эквивалентная потенциальная температура

Поднимающаяся порция воздуха, содержащая водяной пар, если она поднимается достаточно высоко, достигает поднятого уровня конденсации : она насыщается водяным паром (см. соотношение Клаузиуса–Клапейрона ). Если пакет воздуха продолжает подниматься, водяной пар конденсируется и отдает свое скрытое тепло окружающему воздуху, частично компенсируя адиабатическое охлаждение. Поэтому насыщенный воздух при подъеме охлаждается меньше, чем сухой (его температура меняется с высотой при влажно-адиабатическом градиенте , который меньше сухоадиабатического градиента ). Такая насыщенная порция воздуха может достичь плавучести и, таким образом, ускориться дальше вверх, что приводит к состоянию неуправляемости (нестабильности), даже если потенциальная температура увеличивается с высотой. Достаточным условием абсолютной устойчивости столба воздуха даже по отношению к насыщенным конвективным движениям является то, что эквивалентная потенциальная температура должна монотонно возрастать с высотой.

Формула

Определение эквивалентной потенциальной температуры:

$\theta _{e}=T\left({\frac {p_{0}}{p}}\right)^{R_{d}/(c_{pd}+r_{t}c)}H^{-r_{v}R_{v}/(c_{pd}+r_{t}c)}\exp \left[{\frac {L_{v}r_{v}}{(c_{pd}+r_{t}c)T}}\right]$

Где:

• $T$ температура [К] воздуха под давлением $p$,
• $p_{0}$ — эталонное давление, принимаемое за 1000 гПа,
• $p$ давление в точке,
• $R_{d}$ и $R_{v}$ – удельные газовые постоянные сухого воздуха и водяного пара соответственно,
• $c_{pd}$ и $c$ – удельные теплоемкости сухого воздуха и жидкой воды соответственно,
• $r_{t}$ и $r_{v}$ – общие соотношения смешивания воды и водяного пара соответственно,
• $H$ это относительная влажность ,
• $L_{v}$ – скрытая теплота испарения воды.

Для расчета эквивалентной потенциальной температуры используется ряд приближенных формул, поскольку вычислить интегрирование по движению посылки непросто. Болтон (1980) дает обзор таких процедур с оценками ошибок. Его формула наилучшего приближения используется, когда необходима точность:

$\theta _{e}=\theta _{L}\exp \left[\left({\frac {3036}{T_{L}}}-1.78\right)r\left(1+0.448r\right)\right]$

$\theta _{L}=T\left({\frac {p_{0}}{p-e}}\right)^{\kappa _{d}}\left({\frac {T}{T_{L}}}\right)^{0.28r}$

$T_{L}={\frac {1}{{\frac {1}{T_{d}-56}}+{\frac {\log _{e}(T/T_{d})}{800}}}}+56$

Где:

• $\theta _{L}$ (сухая) потенциальная температура [K] на уровне поднятой конденсации (LCL),
• $T_{L}$ (приблизительная) температура [К] при LCL,
• $T_{d}$ температура точки росы под давлением $p$,
• $e$ – давление водяного пара (чтобы получить $\theta _{L}$ для сухого воздуха),
• $\kappa _{d}=R_{d}/c_{pd}$ - отношение удельной газовой постоянной к удельной теплоемкости сухого воздуха при постоянном давлении (0,2854),
• $r$ соотношение массы водяного пара к массе [кг/кг] при смешивании (иногда значение указывается в [г/кг] и это нужно разделить на 1000).

В такой литературе, как Холтон (1972), обычно используется немного более теоретическая формула. когда теоретическое объяснение важно:

$\theta _{e}\approx \theta _{L}\exp \left[{\frac {r_{s}(T_{L})L_{v}(T_{L})}{c_{pd}T_{L}}}\right]$

Где:

• $r_{s}(T_{L})$ - соотношение насыщенной смеси воды при температуре $T_{L}$, температура на уровне насыщения воздуха,
• $L_{v}(T_{L})$ скрытая теплота испарения при температуре $T_{L}$ (от 2406 кДж/кг {при 40 °C} до 2501 кДж/кг {при 0 °C}) и
• $c_{pd}$ – удельная теплоемкость сухого воздуха при постоянном давлении (1005,7 Дж/(кг·К)).

Далее используется более упрощенная формула (например, Stall 1988). §13.1 с. 546) для простоты, если желательно избежать вычислений $T_{L}$:

$\theta _{e}=T_{e}\left({\frac {p_{0}}{p}}\right)^{\kappa _{d}}\approx \left(T+{\frac {L_{v}}{c_{pd}}}r\right)\left({\frac {p_{0}}{p}}\right)^{\frac {R_{d}}{c_{pd}}}$

Где:

• $T_{e}$ = эквивалентная температура
• $R_{d}$ = удельная газовая постоянная для воздуха (287,04 Дж/(кг·К))

Использование

Обратные траектории воздушных масс в период с 31 декабря 1997 г. по январь 1998 г., вызвавшие Североамериканскую ледяную бурю 1998 г.

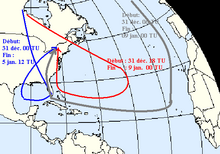
Это применимо в синоптическом масштабе для характеристики воздушных масс. Например, в исследовании ледяной бури в Северной Америке в 1998 году профессора Гьякум ( Университет Макгилла , Монреаль ) и Роббер ( Университет Висконсина-Милуоки ) продемонстрировали, что вовлеченные воздушные массы возникли в высоких широтах Арктики на высоте от 300 до 400 м над уровнем моря. гПа на предыдущей неделе спустились к поверхности по мере продвижения к тропикам, а затем снова двинулись вверх вдоль долины Миссисипи к долине Святого Лаврентия . Обратные траектории оценивались с использованием постоянных эквивалентных потенциальных температур.

В мезомасштабе эквивалентная потенциальная температура также является полезной мерой статической стабильности ненасыщенной атмосферы. В нормальных, устойчиво стратифицированных условиях потенциальная температура увеличивается с высотой.

${\frac {\partial \theta _{e}}{\partial z}}>0$

и вертикальные движения подавляются. Если эквивалентная потенциальная температура уменьшается с высотой,

${\frac {\partial \theta _{e}}{\partial z}}<0$

атмосфера неустойчива к вертикальным движениям, конвекция возможна . Ситуации, когда эквивалентная потенциальная температура уменьшается с высотой, что указывает на нестабильность насыщенного воздуха, довольно распространены.

См. также

• Метеорология
• Влажная статическая энергия
• Потенциальная температура
• Прогноз погоды

Библиография

• М.К. Яу и Р.Р. Роджерс, Краткий курс по физике облаков, третье издание , опубликовано Butterworth-Heinemann, 1 января 1989 г., 304 страницы. ISBN   9780750632157 ISBN   0-7506-3215-1