Квадруполь

Квадруполь — это или квадраполь одна из последовательности конфигураций таких вещей, как электрический заряд, ток или гравитационная масса, которые могут существовать в идеальной форме, но обычно это всего лишь часть мультипольного расширения более сложной структуры, отражающей различные порядки сложности.

Математическое определение

Тензор квадрупольного момента Q второго ранга — представляет собой тензор матрица 3×3. Существует несколько определений, но обычно они даются в бесследовой форме (т.е. $Q_{xx}+Q_{yy}+Q_{zz}=0$ ). Таким образом, тензор квадрупольного момента имеет девять компонентов, но из-за транспозиционной симметрии и свойства нулевого следа в этой форме только пять из них являются независимыми.

Для дискретной системы $\ell$ точечные заряды или массы в случае гравитационного квадруполя , каждый из которых имеет заряд $q_{\ell }$ , или масса $m_{\ell }$ и позиция $\mathbf {r} _{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ относительно начала системы координат компоненты матрицы Q определяются следующим образом:

Q_{ij}=\sum _{\ell }q_{\ell }\left(3r_{i\ell }r_{j\ell }-\left\|\mathbf {r} _{\ell }\right\|^{2}\delta _{ij}\right).

Индексы $i,j$ пробежаться по декартовым координатам $x,y,z$ и $\delta _{ij}$ это дельта Кронекера . Это означает, что $x,y,z$ должно быть с точностью до знака равно расстоянию от точки до $n$ взаимно перпендикулярные гиперплоскости для дельты Кронекера, равной 1.

В бесследовой форме квадрупольный момент иногда выражается как:

Q_{ij}=\sum _{\ell }q_{\ell }r_{i\ell }r_{j\ell }

эта форма находит некоторое применение в литературе относительно метода быстрых мультиполей . Преобразование между этими двумя формами можно легко осуществить с помощью оператора удаления трассировки. ^[1]

Для непрерывной системы с плотностью заряда или плотностью массы $\rho (x,y,z)$ компоненты Q определяются интегралом по декартову пространству r : ^[2]

Q_{ij}=\int \,\rho (\mathbf {r} )\left(3r_{i}r_{j}-\left\|\mathbf {r} \right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Как и в случае с любым мультипольным моментом, если момент низшего порядка, в данном случае монополь или диполь , отличен от нуля, то значение квадрупольного момента зависит от выбора начала координат . Например, диполь двух точечных зарядов одинаковой силы разного знака, который не имеет монопольного момента, может иметь ненулевой квадрупольный момент, если начало координат смещено от центра конфигурации точно между двумя зарядами; или квадрупольный момент можно свести к нулю с началом координат в центре. Напротив, если монопольный и дипольный моменты исчезают, а квадрупольный момент нет, например, четыре заряда одинаковой силы, расположенные в квадрате с чередующимися знаками, то квадрупольный момент не зависит от координат.

Если каждый заряд является источником " $1/r$ Потенциальное поле, как и электрическое или гравитационное поле поля , вклад в потенциал от квадрупольного момента составляет:

V_{\text{q}}(\mathbf {R} )={\frac {k}{|\mathbf {R} |^{3}}}\sum _{i,j}{\frac {1}{2}}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,

где R — вектор с началом в системе зарядов, а — единичный вектор в направлении R. R̂ То есть, ${\hat {R}}_{i}$ для $i=x,y,z$ являются декартовыми компонентами единичного вектора, указывающими от начала координат до точки поля. Здесь, $k$ — константа, которая зависит от типа поля и используемых единиц измерения.

Электрический квадруполь

Контурный график эквипотенциальных поверхностей электрического квадрупольного поля

Простой пример электрического квадруполя состоит из чередующихся положительных и отрицательных зарядов, расположенных по углам квадрата. Монопольный момент (только полный заряд) этого устройства равен нулю. Аналогично, дипольный момент равен нулю, независимо от выбранного начала координат. Но квадрупольный момент устройства на диаграмме нельзя свести к нулю, независимо от того, где мы поместим начало координат. Электрический потенциал квадруполя электрического заряда определяется выражением ^[3]

V_{\text{q}}(\mathbf {R} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {1}{|\mathbf {R} |^{3}}}\sum _{i,j}{\frac {1}{2}}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,

где $\varepsilon _{0}$ - электрическая проницаемость , а $Q_{ij}$ соответствует приведенному выше определению.

Альтернативно, другие источники ^[4] включить половинный коэффициент в $Q_{ij}$ сам тензор, такой что:

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|\mathbf {r} \right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

, и

V_{\text{q}}(\mathbf {R} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {1}{|\mathbf {R} |^{3}}}\sum _{i,j}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,

что делает более явной связь с полиномами Лежандра , возникающими в результате разложения мультиполей, а именно здесь ${\textstyle P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.}$

Обобщение: высшие мультиполи.

Крайним обобщением («точечный осьминог ») может быть: Восемь переменных точечных зарядов в восьми углах параллелепипеда , например куба с длиной ребра a . «Момент октополя» этого устройства будет соответствовать «пределу октополя». ${\textstyle \lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}}$ к ненулевому диагональному тензору третьего порядка. Еще более высокие мультиполи, например, порядка $2^{\ell }$ , будет получено диполярным (квадрупольным, октополярным, ...) расположением точечных диполей (квадруполей, октополей, ...), а не точечных монополей более низкого порядка, например, $2^{\ell -1}$ .

Магнитный квадруполь

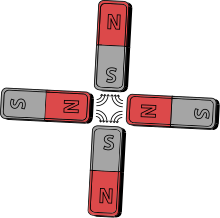
Все известные магнитные источники дают дипольные поля. Однако можно создать магнитный квадруполь, разместив четыре одинаковых стержневых магнита перпендикулярно друг другу так, чтобы северный полюс одного находился рядом с южным полюсом другого. Такая конфигурация нейтрализует дипольный момент и дает квадрупольный момент, причем его поле будет убывать на больших расстояниях быстрее, чем у диполя.

Пример магнитного квадруполя с постоянными магнитами изображен справа. Электромагниты аналогичной концептуальной конструкции (называемые квадрупольными магнитами ) обычно используются для фокусировки пучков заряженных частиц в ускорителях частиц и линиях транспортировки пучков — метод, известный как сильная фокусировка . Имеется четыре стальных наконечника полюса, два противоположных северных магнитных полюса и два противоположных магнитных южных полюса. Сталь намагничивается сильным электрическим током , который течет по катушкам трубок, обернутым вокруг полюсов.

Изменение магнитного квадрупольного момента производит электромагнитное излучение .

Гравитационный квадруполь

Квадруполь массы аналогичен квадруполю электрического заряда, где плотность заряда просто заменяется плотностью массы и добавляется отрицательный знак, поскольку массы всегда положительны, а сила притяжения. Тогда гравитационный потенциал выражается как:

V_{\text{q}}(\mathbf {R} )=-{\frac {G}{2|\mathbf {R} |^{3}}}\sum _{i,j}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ .

Например, поскольку Земля вращается, она сплющена (сплющена на полюсах). Это дает ему ненулевой квадрупольный момент. Хотя вклад этого квадруполя в гравитационное поле Земли чрезвычайно важен для искусственных спутников, близких к Земле, он менее важен для Луны, поскольку ${1}/{|\mathbf {R} |^{3}}$ срок быстро падает.

Массовый квадрупольный момент также важен в общей теории относительности , поскольку, если он изменяется во времени, он может производить гравитационное излучение , подобное электромагнитному излучению, создаваемому колеблющимися электрическими или магнитными диполями и высшими мультиполями. Однако гравитационно излучать могут только квадрупольные и более высокие моменты. Монополь массы представляет собой полную массу-энергию в системе, которая сохраняется — поэтому не излучает излучения. Точно так же диполь массы соответствует центру масс системы, а его первая производная представляет импульс, который также является сохраняющейся величиной, поэтому диполь массы также не излучает излучения. Однако масса квадруполя может меняться во времени и представляет собой вклад самого низкого порядка в гравитационное излучение. ^[5]

Самый простой и наиболее важный пример излучающей системы — это пара точек с равными массами, вращающихся вокруг друг друга по круговой орбите, что является приближением, например, к частному случаю двойных черных дыр . Поскольку дипольный момент постоянен, мы можем для удобства разместить начало координат прямо между двумя точками. Тогда дипольный момент будет равен нулю, а если еще и масштабировать координаты так, чтобы точки находились на единице расстояния от центра, в противоположном направлении, то квадрупольный момент системы тогда будет просто равен

Q_{ij}=M\left(3x_{i}x_{j}-|\mathbf {x} |^{2}\delta _{ij}\right)

где M - масса каждой точки, а $x_{i}$ являются компонентами (единичного) вектора положения одной из точек. По мере вращения этот x -вектор будет вращаться, а это означает, что он будет иметь ненулевую первую, а также ненулевую вторую производную по времени (это, конечно, верно независимо от выбора системы координат). Следовательно, система будет излучать гравитационные волны. Энергия, теряемая таким образом, впервые наблюдалась в период изменения двойной системы Халса-Тейлора , пульсара, находящегося на орбите с другой нейтронной звездой аналогичной массы.

Подобно тому, как мультиполи электрического заряда и тока вносят вклад в электромагнитное поле, мультиполи массы и массового тока вносят вклад в гравитационное поле в общей теории относительности, вызывая так называемые гравитомагнитные эффекты. Изменение мультиполей массового тока также может вызывать гравитационное излучение. Однако вклад токовых мультиполей обычно будет намного меньше, чем вклад массового квадруполя.

См. также

Ссылки

^ Эпплквист, Дж. (1989). «Бесследовые декартовы тензорные формы для сферических гармонических функций: новые теоремы и приложения к электростатике диэлектрических сред». Журнал физики A: Математический и общий . 22 (20): 4303–4330. Бибкод : 1989JPhA...22.4303A . дои : 10.1088/0305-4470/22/20/011 .
^ Вайсштейн, Эрик. «Электрический квадрупольный момент» . Мир физики Эрика Вайсштейна . Вольфрамовые исследования . Проверено 8 мая 2012 г.
^ Джексон, Джон Дэвид (1975). Классическая электродинамика . Джон Уайли и сыновья . ISBN 0-471-43132-Х .
^ Гриффитс, Дэвид Дж. (2013). Введение в электродинамику, 4-е изд . Пирсон. п. 153 165.
^ Торн, Кип С. (апрель 1980 г.). «Многополюсное расширение гравитационного излучения» (PDF) . Обзоры современной физики . 52 (2): 299–339. Бибкод : 1980РвМП...52..299Т . дои : 10.1103/RevModPhys.52.299 .

Внешние ссылки

Многополюсное расширение

[1] Эпплквист, Дж. (1989). «Бесследовые декартовы тензорные формы для сферических гармонических функций: новые теоремы и приложения к электростатике диэлектрических сред». Журнал физики A: Математический и общий . 22 (20): 4303–4330. Бибкод : 1989JPhA...22.4303A . дои : 10.1088/0305-4470/22/20/011 .

[wolf_eqm-2] Вайсштейн, Эрик. «Электрический квадрупольный момент» . Мир физики Эрика Вайсштейна . Вольфрамовые исследования . Проверено 8 мая 2012 г.

[3] Джексон, Джон Дэвид (1975). Классическая электродинамика . Джон Уайли и сыновья . ISBN 0-471-43132-Х .

[4] Гриффитс, Дэвид Дж. (2013). Введение в электродинамику, 4-е изд . Пирсон. п. 153 165.

[5] Торн, Кип С. (апрель 1980 г.). «Многополюсное расширение гравитационного излучения» (PDF) . Обзоры современной физики . 52 (2): 299–339. Бибкод : 1980РвМП...52..299Т . дои : 10.1103/RevModPhys.52.299 .

[1]

[2]

[3]

[4]

[5]