Многополярное обменное взаимодействие

Магнитные материалы с сильным спин-орбитальным взаимодействием , такие как: LaFeAsO, ПрФе ₄ П ₁₂ , YbRu ₂ Ge ₂ , УО ₂ , НпО ₂ , Ce _1−x La _x B ₆ , УРу ₂ Си ₂ и многие другие соединения имеют магнитное упорядочение, состоящее из мультиполей высокого ранга, например четверного, октопного и т. д. Из-за сильной спин-орбитальной связи в системах автоматически вводятся мультиполи, когда полное квантовое число углового момента J превышает 1/2. Если эти мультиполи связаны некоторыми механизмами обмена, эти мультиполи могут иметь некоторый порядок, как в обычной задаче Гейзенберга со спином 1/2. За исключением многополярного упорядочения, многие явления скрытого порядка, как полагают, тесно связаны с многополярными взаимодействиями.

Расширение тензорного оператора

Основные понятия

Рассмотрим квантовомеханическую систему с гильбертовым пространством, натянутым на $|j,m_{j}\rangle$, где $j$ - полный угловой момент и $m_{j}$ – его проекция на ось квантования. Тогда любые квантовые операторы можно представить с помощью базисного набора $\lbrace |j,m_{j}\rangle \rbrace$ как матрица с размерностью $(2j+1)$. Следовательно, можно определить $(2j+1)^{2}$ матрицы для полного расширения любого квантового оператора в этом гильбертовом пространстве. Взяв в качестве примера J=1/2, квантовый оператор A можно разложить как

$A={\begin{bmatrix}1&2\\3&4\end{bmatrix}}=1{\begin{bmatrix}1&0\\0&0\end{bmatrix}}+2{\begin{bmatrix}0&1\\0&0\end{bmatrix}}+3{\begin{bmatrix}0&0\\1&0\end{bmatrix}}+4{\begin{bmatrix}0&0\\0&1\end{bmatrix}}=1L_{1,1}+2L_{1,2}+3L_{2,1}+4L_{2,2}$

Очевидно, что матрицы: $L_{ij}=|i\rangle \langle j|$ образуют базисный набор в пространстве операторов. Любой квантовый оператор, определенный в этом Гильберте, может быть израсходован $\lbrace L_{ij}\rbrace$ операторы. В дальнейшем давайте называть эти матрицы супербазисом, чтобы различать собственный базис квантовых состояний. Точнее, приведенная выше супербаза $\lbrace L_{ij}\rbrace$ можно назвать супербазисом перехода, поскольку он описывает переход между состояниями $|i\rangle$ и $|j\rangle$. На самом деле, это не единственная супероснова, которая делает свое дело. Мы также можем использовать матрицы Паули и единичную матрицу для формирования супербазиса.

$A={\begin{bmatrix}1&2\\3&4\end{bmatrix}}={\frac {5}{2}}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}+{\frac {i}{2}}{\begin{bmatrix}0&i\\-i&0\end{bmatrix}}+{\frac {3}{2}}{\begin{bmatrix}-1&0\\0&1\end{bmatrix}}+{\frac {5}{2}}{\begin{bmatrix}0&1\\1&0\end{bmatrix}}={\frac {5}{2}}I+{\frac {i}{2}}\sigma _{y}+{\frac {3}{2}}\sigma _{z}+{\frac {5}{2}}\sigma _{x}$

Поскольку свойства вращения $\sigma _{x},\sigma _{y},\sigma _{z}$ подчиняются тем же правилам, что и тензор кубических гармоник первого ранга. $T_{x},T_{y},T_{z}$ и единичная матрица $I$ следует тем же правилам, что и тензор ранга 0 $T_{s}$, базисный набор $\lbrace I,\sigma _{x},\sigma _{y},\sigma _{z}\rbrace$ можно назвать кубическим супербазисом. Другим часто используемым супербазисом является сферический гармонический супербазис, который строится путем замены $\sigma _{x},\ \sigma _{y}$ операторам подъема и опускания $\lbrace I,\sigma _{-1},\sigma _{0},\sigma _{+1}\rbrace$

$A={\begin{bmatrix}1&2\\3&4\end{bmatrix}}={\frac {5}{2}}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}+2{\begin{bmatrix}0&1\\0&0\end{bmatrix}}+{\frac {3}{2}}{\begin{bmatrix}-1&0\\0&1\end{bmatrix}}-3{\begin{bmatrix}0&0\\-1&0\end{bmatrix}}={\frac {5}{2}}I+2\sigma _{+1}+{\frac {3}{2}}\sigma _{0}-3\sigma _{-1}$

Снова, $\sigma _{-1},\sigma _{0},\sigma _{+1}$ имеют те же вращательные свойства, что и тензоры сферических гармоник 1-го ранга. $Y_{-1}^{1},Y_{0}^{1},Y_{-1}^{1}$, поэтому его называют сферическим супербазисом.

Потому что атомные орбитали $s,p,d,f$ также описываются сферическими или кубическими гармоническими функциями, эти операторы можно представить или визуализировать, используя волновые функции атомных орбиталей, хотя по сути они являются матрицами, а не пространственными функциями.

Если мы расширим проблему до $J=1$, нам понадобится 9 матриц, чтобы сформировать супербазис. Для переходного супербазиса мы имеем $\lbrace L_{ij};i,j=1\sim 3\rbrace$. Для кубического супербазиса имеем $\lbrace T_{s},T_{x},T_{y},T_{z},T_{xy},T_{yz},T_{zx},T_{x^{2}-y^{2}},T_{3z^{2}-r^{2}}\rbrace$. Для сферического супербазиса имеем $\lbrace Y_{0}^{0},Y_{-1}^{1},Y_{0}^{1},Y_{-1}^{1},Y_{-2}^{2},Y_{-1}^{2},Y_{0}^{2},Y_{1}^{2},Y_{2}^{2}\rbrace$. В теории групп, $T_{s}/Y_{0}^{0}$ называются скаляром или тензором ранга 0, $T_{x,yz,}/Y_{-1,0,+1}^{1}$ называются дипольными или тензорами ранга 1, $T_{xy,yz,zx,x^{2}-y^{2},3z^{2}-r^{2}}/Y_{-2,-1,0,+1,+2}^{2}$ называются квадрупольными тензорами или тензорами ранга 2.

Пример показывает нам, что для $J$- задача мультиплета, нужны все ранги $0\sim 2J$ тензорные операторы для формирования полного супербазиса. Следовательно, для $J=1$ системы ее матрица плотности должна иметь квадрупольные компоненты. Это причина, по которой $J>1/2$ проблема автоматически введет в систему мультиполи высокого ранга

Формальные определения

матричные элементы и действительная часть соответствующих гармонических функций кубического операторного базиса в случае J=1.

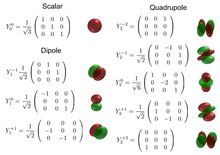
Общее определение сферического гармонического супербазиса $J$-мультиплетная задача может быть выражена как

$Y_{K}^{Q}(J)=\sum _{MM^{\prime }}(-1)^{J-M}(2K+1)^{1/2}\times \left({\begin{matrix}J&J&K\\M^{^{\prime }}&-M&Q\end{matrix}}\right)|JM\rangle \langle JM^{^{\prime }}|,$

где круглые скобки обозначают 3-j символ ; K - ранг, который колеблется $0\sim 2J$; Q - это индекс проекции ранга K, который находится в диапазоне от −K до +K. Супербазис кубической гармоники, в котором все тензорные операторы являются эрмитовыми, можно определить как

$T_{K}^{Q}={\frac {1}{\sqrt {2}}}[(-1)^{Q}Y_{K}^{Q}(J)+Y_{K}^{-Q}(J)]$

$T_{K}^{-Q}={\frac {i}{\sqrt {2}}}[Y_{K}^{Q}(J)-(-1)^{Q}Y_{K}^{-Q}(J)]$

Тогда любой квантовый оператор $A$ определены в $J$-мультиплетное гильбертово пространство можно расширить как

$A=\sum _{K,Q}\alpha _{K}^{Q}Y_{K}^{Q}=\sum _{K,Q}\beta _{K}^{Q}T_{K}^{Q}=\sum _{i,j}\gamma _{i,j}L_{i,j}$

где коэффициенты разложения можно получить, взяв след внутреннего продукта, например $\alpha _{K}^{Q}=Tr[AY_{K}^{Q\dagger }]$. По-видимому, можно составить линейную комбинацию этих операторов, чтобы сформировать новый супербазис, имеющий другую симметрию.

Описание мультибиржи

Используя теорему сложения тензорных операторов, произведение тензора ранга n и тензора ранга m может породить новый тензор с рангом n+m ~ |nm|. Следовательно, тензор высокого ранга можно выразить как произведение тензоров низкого ранга. Это соглашение полезно для интерпретации членов многополярного обмена высокого ранга как процесса «многообмена» диполей (или псевдоспинов). Например, для операторов тензора сферических гармоник $J=1$ случай, у нас есть

$Y_{2}^{-2}=2Y_{1}^{-1}Y_{1}^{-1}$

$Y_{2}^{-1}={\sqrt {2}}(Y_{1}^{-1}Y_{1}^{0}+Y_{1}^{0}Y_{1}^{-1})$

$Y_{2}^{0}={\sqrt {24}}/6(Y_{1}^{-1}Y_{1}^{+1}+2Y_{1}^{0}Y_{1}^{0}+Y_{1}^{+1}Y_{1}^{-1})$

$Y_{2}^{+1}={\sqrt {2}}(Y_{1}^{0}Y_{1}^{+1}+Y_{1}^{+1}Y_{1}^{0})$

$Y_{2}^{+2}=2Y_{1}^{+1}Y_{1}^{+1}$

Если это так, то квадруполь-квадрупольное взаимодействие (см. следующий раздел) можно рассматривать как двухступенчатое диполь-дипольное взаимодействие. Например, $Y_{2_{i}}^{+2_{i}}Y_{2_{j}}^{-2_{j}}=4Y_{1_{i}}^{+1_{i}}Y_{1_{i}}^{+1_{i}}Y_{1_{j}}^{-1_{j}}Y_{1_{j}}^{-1_{j}}$, поэтому одношаговый квадрупольный переход $Y_{2_{i}}^{+2_{i}}$ на месте $i$ теперь становится двухступенчатым дипольным переходом $Y_{1_{i}}^{+1_{i}}Y_{1_{i}}^{+1_{i}}$. Следовательно, возникают условия не только межсайтового обмена, но и внутрисайтового обмена (так называемый мультиобмен). Если $J$ еще больше, можно ожидать появления более сложных условий внутрисайтового обмена. Однако следует отметить, что это не разложение по возмущениям, а всего лишь математический прием. Термины высокого ранга не обязательно меньше терминов низкого ранга. Во многих системах термины высокого ранга более важны, чем термины низкого ранга.

Многополярные обменные взаимодействия

Примеры диполь-дипольного и квадруполь-квадрупольного обменного взаимодействия в случае J=1. Синяя стрелка означает, что переход сопровождается $\pi$фазовый сдвиг.

Существует четыре основных механизма, вызывающих обменное взаимодействие между двумя магнитными моментами в системе: 1). Прямой обмен 2). РККИ 3). Супербиржа 4). Спиновая решетка. Независимо от того, какой из них преобладает, общий вид обменного взаимодействия можно записать как

$H=\sum _{ij}\sum _{KQ}C_{K_{i}K_{j}}^{Q{i}Q_{j}}T_{K_{i}}^{Q_{i}}T_{K_{j}}^{Q_{j}}$

где $i,j$ индексы сайта и $C_{K_{i}K_{j}}^{Q{i}Q_{j}}$ - константа связи, связывающая два мультипольных момента $T_{K_{i}}^{Q_{i}}$ и $T_{K_{j}}^{Q_{j}}$. Можно сразу найти, если $K$ ограничено только единицей, гамильтониан сводится к обычной модели Гейзенберга.

Важной особенностью многополярного обменного гамильтониана является его анизотропия. Значение константы связи $C_{K_{i}K_{j}}^{Q{i}Q_{j}}$ обычно очень чувствителен к относительному углу между двумя мультиполями. В отличие от обычного гамильтониана только спинового обмена, где константы связи изотропны в однородной системе, сильно анизотропные атомные орбитали (напомним форму $s,p,d,f$ волновые функции) связь с магнитными моментами системы неизбежно приведет к огромной анизотропии даже в однородной системе. Это одна из основных причин того, что большинство многополярных порядков имеют тенденцию быть неколлинеарными.

Антиферромагнетизм многополярных моментов.

Переключение фаз мультиполей

АФМ упорядочивает цепочки различных мультиполей.

В отличие от магнитного спинового упорядочения, где антиферромагнетизм можно определить путем переворота оси намагничивания двух соседних узлов из ферромагнитной конфигурации, переворот оси намагничивания мультиполя обычно бессмысленен. Принимая $T_{yz}$ момент в качестве примера, если перевернуть ось Z, сделав $\pi$ вращение к оси Y, это просто ничего не меняет. Поэтому предлагаемое определение антиферромагнитного мультиполярного упорядочения заключается в перевороте их фаз путем $\pi$, то есть $T_{yz}\rightarrow e^{i\pi }T_{yz}=-T_{yz}$. В этом отношении антиферромагнитное спиновое упорядочение является лишь частным случаем этого определения, т.е. переворот фазы дипольного момента эквивалентен перевороту его оси намагничивания. Что касается мультиполей высокого ранга, например $T_{yz}$, это фактически становится $\pi /2$ вращения и для $T_{3z^{2}-r^{2}}$ это даже не какое-то вращение.

Вычисление констант связи

Расчет многополярных обменных взаимодействий остается сложной задачей во многих аспектах. Хотя было много работ, основанных на сопоставлении модельных гамильтонианов с экспериментами, предсказания констант связи, основанные на схемах из первых принципов, по-прежнему отсутствуют. В настоящее время существуют два исследования, реализующие первопринципный подход к изучению многополярных обменных взаимодействий. Раннее исследование было разработано в 80-х годах. Он основан на подходе среднего поля, который может значительно уменьшить сложность констант связи, индуцированных механизмом РККИ, поэтому многополярный обменный гамильтониан можно описать всего несколькими неизвестными параметрами и получить путем подбора экспериментальных данных. Позже подход из первых принципов для оценки неизвестных параметров получил дальнейшее развитие и получил хорошее согласие с несколькими выбранными соединениями, например, момпниктидами церия. Недавно был предложен и другой подход, основанный на принципах первопринципов. Он сопоставляет все константы связи, индуцированные всеми механизмами статического обмена, с серией расчетов полной энергии DFT + U и согласовывает их с диоксидом урана.