Электромагнит

Для более широкого освещения этой темы см. Электромагнетизм .

Простой электромагнит, состоящий из катушки проволоки, намотанной на железный сердечник. Сердечник из ферромагнитного материала, такого как железо, служит для увеличения создаваемого магнитного поля. Сила создаваемого магнитного поля пропорциональна силе тока через обмотку.

Магнитное поле, создаваемое соленоидом ( катушкой с проводом). На этом рисунке показано поперечное сечение центра катушки. Крестики — это провода, по которым ток поступает на страницу; точки — это провода, по которым ток выходит за пределы страницы.

Электромагнит , — это тип магнита в котором магнитное поле создается электрическим током . Электромагниты обычно состоят из проволоки, намотанной в катушку . Ток по проводу создает магнитное поле, которое концентрируется в отверстии в центре катушки . Магнитное поле исчезает при выключении тока. Витки провода часто наматываются на магнитный сердечник , изготовленный из ферромагнитного или ферримагнитного материала, например железа ; магнитный сердечник концентрирует магнитный поток и делает магнит более мощным.

Основное преимущество электромагнита перед постоянным магнитом состоит в том, что магнитное поле можно быстро изменять, контролируя величину электрического тока в обмотке. Однако, в отличие от постоянного магнита, которому не требуется питание, электромагниту требуется непрерывная подача тока для поддержания магнитного поля.

Электромагниты широко используются в качестве компонентов других электрических устройств, таких как двигатели , генераторы , электромеханические соленоиды , реле , громкоговорители , жесткие диски , аппараты МРТ , научные инструменты и оборудование для магнитной сепарации . Электромагниты также используются в промышленности для подъема и перемещения тяжелых железных предметов, таких как железный лом и сталь.

История

Электромагнит Осетра, 1824 г.

Один из электромагнитов Генри, способный поднимать сотни фунтов, 1830-е годы.

Крупный план большого электромагнита Генри

Датский ученый Ганс Кристиан Эрстед в 1820 году обнаружил, что электрические токи создают магнитные поля. В том же году французский учёный Андре-Мари Ампер показал, что железо можно намагничивать, поместив его в соленоид с электрическим питанием. Британский ученый Уильям Стерджен изобрел электромагнит в 1824 году. Его первый электромагнит представлял собой кусок железа в форме подковы, обмотанный примерно 18 витками голой медной проволоки ( изолированного провода тогда не существовало). Железо покрыли лаком, чтобы изолировать его от обмоток. Когда через катушку пропускали ток, железо намагничивалось и притягивало к себе другие куски железа; когда ток прекращался, он терял намагниченность. Осетр продемонстрировал свою силу, показав, что, хотя он весил всего семь унций (примерно 200 граммов), он мог поднять девять фунтов (примерно 4 килограмма) при подаче тока от одноэлементного источника питания. Однако магниты Стерджена были слабыми, потому что неизолированный провод, который он использовал, можно было обернуть только одним слоем вокруг сердечника, что ограничивало количество витков.

Начиная с 1830 года американский учёный Джозеф Генри систематически улучшал и популяризировал электромагнит. Используя провод, изолированный шелковой нитью, вдохновленный использованием Швайгером нескольких витков провода для изготовления гальванометра , он смог намотать несколько слоев проволоки на сердечники, создав мощные магниты с тысячами витков проволоки, в том числе тот, который выдерживал 2063 фунта (936 кг). Первое крупное применение электромагнитов было в телеграфных эхолотах .

Теория магнитных доменов того, как работают ферромагнитные сердечники, была впервые предложена в 1906 году французским физиком Пьером-Эрнестом Вайсом , а подробная современная квантово-механическая теория ферромагнетизма была разработана в 1920-х годах Вернером Гейзенбергом , Львом Ландау , Феликсом Блохом и другими.

Применение электромагнитов

Промышленный электромагнит, поднимающий металлолом, 1914 год.

Портативный электромагнит предназначен для удержания материала на месте; примером является подъемный магнит. применяет Тяговый электромагнит силу и что-то перемещает.

Электромагниты очень широко используются в электрических и электромеханических устройствах, в том числе:

• Двигатели и генераторы
• Трансформеры
• Реле
• Электрические звонки и зуммеры
• Громкоговорители и наушники
• Приводы, такие как клапаны
• магнитной записи Аппаратура и хранения данных: магнитофоны , видеомагнитофоны , жесткие диски.
• МРТ Аппараты
• Научное оборудование, такое как масс-спектрометры.
• Ускорители частиц
• Магнитные замки
• Оборудование для магнитной сепарации используется для отделения магнитных материалов от немагнитных, например, для отделения черного металла от других материалов в металлоломе.
• Промышленные подъемные магниты
• магнитная левитация , используемая в поезде или поездах на магнитной подвеске
• Индукционный нагрев для приготовления пищи, производства и гипертермической терапии.

Лабораторный электромагнит. Создает поле 2 Тл с током 20 А.

Магнит в масс-спектрометре

на статоре электродвигателя Электромагнит переменного тока

Магниты в электрическом звонке

Шестипольный фокусирующий магнит в синхротроне.

Простой соленоид

Основная статья: Соленоид

Обычный тяговый электромагнит представляет собой соленоид и плунжер с равномерной обмоткой. Соленоид представляет собой катушку с проволокой, а плунжер изготовлен из такого материала, как мягкое железо. Подача тока на соленоид прикладывает силу к плунжеру и может заставить его двигаться. Плунжер перестает двигаться, когда действующие на него силы уравновешиваются. Например, силы уравновешиваются, когда плунжер центрирован в соленоиде.

Максимальное равномерное натяжение происходит, когда один конец плунжера находится в середине соленоида. Приближение силы F :

$F={\frac {CANI}{\ell }}$

где C — константа пропорциональности, A — площадь поперечного сечения плунжера, N — количество витков соленоида, I — ток через провод соленоида, а ℓ — длина соленоида. Для устройств, использующих силу в дюймах, фунтах и ​​амперах с длинными тонкими соленоидами, значение C составляет от 0,009 до 0,010 фунтов на квадратный дюйм (максимальное усилие в фунтах на квадратный дюйм площади поперечного сечения плунжера). Например, катушка длиной 12 дюймов ( ℓ = 12 дюймов ) с длинным плунжером поперечного сечения 1 квадратный дюйм ( A = 1 дюйм). ² ) и 11 200 ампер-витков ( NI = 11 200 Aturn ) имели максимальное усилие 8,75 фунта (что соответствует C = 0,0094 фунта на квадратный дюйм ).

Максимальное усилие увеличивается, когда в соленоид вставлен магнитный стопор. Ограничитель становится магнитом, притягивающим поршень; он мало увеличивает тяговое усилие соленоида, когда плунжер находится далеко, но значительно увеличивает тяговое усилие, когда они близко. Приближение для тяги P :

$P=ANI\left[{\frac {NI}{(\ell _{\mathrm {a} })^{2}(C_{1})^{2}}}+{\frac {C}{\ell }}\right]={\frac {AN^{2}I^{2}}{(\ell _{\mathrm {a} })^{2}(C_{1})^{2}}}+{\frac {CANI}{\ell }}$

Здесь ℓa _— расстояние между концом упора и концом плунжера. Дополнительная константа C ₁ для единиц дюймов, фунтов и ампер с тонкими соленоидами составляет около 2660. Второй член в скобках представляет ту же силу, что и безостановочный соленоид выше; первый член представляет собой притяжение между упором и плунжером.

В базовую конструкцию можно внести некоторые улучшения. Концы упора и плунжера часто имеют коническую форму. Например, плунжер может иметь заостренный конец, который входит в соответствующую выемку в упоре. Форма делает натяжение соленоида более равномерным в зависимости от разделения. Еще одним улучшением является добавление обратного магнитного пути вокруг соленоида («соленоид с железной оболочкой»). Путь магнитного возврата, как и стопор, оказывает незначительное влияние, пока воздушный зазор не станет небольшим.

Физика

Текущий ( $I$) через провод создает магнитное поле ( $B$). Поле ориентировано по правилу правой руки .

Линии магнитного поля проволочной петли с током проходят через центр петли, концентрируя там поле.

Магнитное поле, создаваемое прохождением тока через катушку

Электрический ток, текущий по проводу, создает вокруг провода магнитное поле согласно закону Ампера (см. рисунок провода с магнитным полем) . Для концентрации магнитного поля в электромагните проволоку наматывают в катушку, в которой множество витков проволоки лежит рядом. Магнитное поле всех витков провода проходит через центр катушки, создавая там сильное магнитное поле. Катушка, имеющая форму прямой трубки ( спирали ), называется соленоидом .

Направление магнитного поля через катушку с проводом можно найти по правилу правой руки . Если пальцы правой руки обхватить катушку по направлению тока ( условного тока , потока положительного заряда ) через обмотки, то большой палец укажет в направлении поля внутри катушки. Сторона магнита, из которой выходят силовые линии, определяется как северный полюс .

Магнитный сердечник

Определения переменных ниже см. в рамке в конце статьи.

Гораздо более сильные магнитные поля можно создать, если « магнитный сердечник » из мягкого ферромагнитного (или ферримагнитного ) материала, такого как железо . внутри катушки поместить Сердечник может увеличить магнитное поле в тысячи раз по сравнению с силой поля одной катушки из-за высокой магнитной проницаемости материала μ. Не во всех электромагнитах используются сердечники, поэтому их называют электромагнитами с ферромагнитным или железным сердечником.

Это связано с тем, что материал магнитного сердечника (часто изготовленный из железа или стали) состоит из небольших областей, называемых магнитными доменами , которые действуют как крошечные магниты (см. Ферромагнетизм ). До включения тока в электромагните домены в сердечнике из мягкого железа направлены в случайных направлениях, поэтому их крошечные магнитные поля нейтрализуют друг друга, и железо не имеет крупномасштабного магнитного поля. Когда ток проходит через провод, обернутый вокруг железа, его магнитное поле проникает в железо и заставляет домены поворачиваться, выравниваясь параллельно магнитному полю, поэтому их крошечные магнитные поля добавляются к полю провода, создавая большое магнитное поле. которая простирается в пространство вокруг магнита. Эффект сердечника заключается в концентрации поля, и магнитное поле проходит через сердечник с меньшим сопротивлением , чем когда оно проходило бы через воздух.

Чем больший ток проходит через проволочную катушку, тем больше выравниваются домены и тем сильнее магнитное поле. Наконец, все домены выстраиваются в линию, и дальнейшее увеличение тока вызывает лишь незначительное увеличение магнитного поля: это явление называется насыщением . Вот почему самые сильные электромагниты, такие как сверхпроводящие и очень сильноточные электромагниты, не могут использовать сердечники.

Основная нелинейная особенность ферромагнетиков состоит в том, что поле B насыщается при определенной величине: что составляет от 1,6 до 2 Тл (Тл) для большинства сталей с высокой магнитной проницаемостью. Поле B быстро увеличивается с увеличением тока до этого значения, но выше этого значения поле выравнивается и становится почти постоянным, независимо от того, какой ток проходит через обмотки. Максимальная сила магнитного поля, возможная от электромагнита с железным сердечником, ограничена примерно от 1,6 до 2 Тл.

Когда ток в катушке отключается, в магнитомягких материалах, которые почти всегда используются в качестве сердечников, большинство доменов теряют выравнивание и возвращаются в случайное состояние, и поле исчезает. Однако некоторая часть выравнивания сохраняется, поскольку домены с трудом меняют направление намагничивания, в результате чего ядро ​​становится намагниченным как слабый постоянный магнит. Это явление называется гистерезисом , а остаточное магнитное поле называется остаточным магнетизмом . Остаточную намагниченность сердечника можно удалить путем размагничивания . В электромагнитах переменного тока, например, используемых в двигателях, намагниченность сердечника постоянно меняется на противоположную, и остаточная намагниченность способствует потерям в двигателе.

Закон Ампера

Магнитное поле электромагнитов в общем случае определяется законом Ампера :

$\int \mathbf {J} \cdot d\mathbf {A} =\oint \mathbf {H} \cdot d{\boldsymbol {\ell }}$

который говорит, что интеграл намагничивающего поля $\mathbf {H}$ вокруг любого замкнутого контура равна сумме тока, протекающего через контур. Другое используемое уравнение, которое определяет магнитное поле, создаваемое каждым небольшим сегментом тока, — это закон Био-Савара .

Сила, действующая магнитным полем

Аналогично соленоиду сила, действующая со стороны электромагнита на проводник, расположенный на участке материала сердечника, равна:

$F={\frac {B^{2}A}{2\mu _{0}}}$ ( 1 )

Уравнение силы можно вывести из энергии, запасенной в магнитном поле . Энергия — это сила, умноженная на расстояние. Перестановка членов дает приведенное выше уравнение.

Предел 1,6 Тл на поле упомянутое выше устанавливает предел максимальной силы на единицу площади сердечника или магнитного давления , которое может оказывать электромагнит со железным сердечником; грубо:

${\frac {F}{A}}={\frac {(B_{\text{sat}})^{2}}{2\mu _{0}}}\approx 1000\ \mathrm {kPa} =10^{6}\mathrm {N/m^{2}} =145\ \mathrm {lbf/in^{2}}$

для предела насыщения активной зоны B _sat .В более интуитивно понятных единицах полезно помнить, что при 1 Тл магнитное давление составляет примерно 4 атмосферы или кг/см. ² .

Учитывая геометрию ядра, поле B, необходимое для данной силы, можно рассчитать по формуле (1); если оно окажется намного больше 1,6 Тл, необходимо использовать сердечник большего размера.

Однако вычисление магнитного поля и силы, действующей на ферромагнитные материалы, в целом затруднено по двум причинам. Во-первых, потому что напряженность поля меняется от точки к точке сложным образом, особенно за пределами активной зоны и в воздушных зазорах, где краевые поля и поток рассеяния необходимо учитывать . Во-вторых, потому что магнитное поле B и сила являются нелинейными функциями тока и зависят от нелинейного соотношения между B и H для конкретного используемого материала сердечника. компьютерные программы, позволяющие построить модель магнитного поля методом конечных элементов Для точных расчетов используются .

Магнитная цепь

Магнитное поле ( зеленое ) типичного электромагнита с железным сердечником C, образующим замкнутый контур с двумя воздушными зазорами G в нем.
Б – магнитное поле в сердечнике
Б _Ф – «окаймляющие поля». В зазорах G силовые линии магнитного поля «выпирают», поэтому напряженность поля меньше, чем в сердечнике: B _F < B
B _L – поток рассеяния ; линии магнитного поля, которые не следуют полной магнитной цепи
L – средняя длина магнитной цепи, используемой в уравнении. 1 ниже. Это сумма длины L _{сердечника} в железных сердечниках и длины L _зазора в воздушных G. зазорах
И поток рассеяния, и краевые поля увеличиваются по мере увеличения зазоров, уменьшая силу, действующую со стороны магнита.

Во многих практических применениях электромагнитов, таких как двигатели, генераторы, трансформаторы, подъемные магниты и громкоговорители, железный сердечник имеет форму петли или магнитной цепи , возможно, разорванной несколькими узкими воздушными зазорами. Железо оказывает гораздо меньшее «сопротивление» ( сопротивление ) магнитному полю, чем воздух, поэтому можно получить более сильное поле, если большая часть пути магнитного поля проходит внутри сердечника. Вот почему сердечник и силовые линии магнитного поля имеют форму замкнутых петель.

Поскольку большая часть магнитного поля ограничена контурами сердечника, это позволяет упростить математический анализ. См. рисунок справа. Общее упрощающее предположение, которому удовлетворяют многие электромагниты и которое будет использоваться в этом разделе, заключается в том, что напряженность магнитного поля B постоянна вокруг магнитной цепи (внутри сердечника и воздушных зазоров) и равна нулю вне ее. Большая часть магнитного поля будет сосредоточена в материале сердечника ( C ). Внутри сердечника магнитное поле ( B ) будет примерно однородным по всему поперечному сечению, поэтому, если, кроме того, сердечник имеет примерно постоянную площадь по всей своей длине, поле в сердечнике будет постоянным. Это просто оставляет воздушные зазоры ( G ), если таковые имеются, между секциями сердцевины. В зазорах линии магнитного поля больше не ограничиваются сердечником, поэтому они «выступают» за контуры сердечника, а затем изгибаются назад, чтобы войти в следующий кусок материала сердечника, уменьшая напряженность поля в зазоре. Выпуклости ( B _F ) называются окаймляющими полями . Однако пока длина зазора меньше размеров поперечного сечения сердечника, поле в зазоре будет примерно таким же, как и в сердечнике. Кроме того, некоторые из силовых линий магнитного поля ( BL _{) будут «короткими путями» и не пройдут через всю цепь сердечника и, таким образом ,} не будут способствовать силе, действующей со стороны магнита. Сюда также входят линии поля, которые окружают обмотки проводов, но не входят в сердечник. Это называется потоком утечки . Следовательно, уравнения в этом разделе справедливы для электромагнитов, для которых:

1. магнитная цепь представляет собой единую петлю из материала сердечника, возможно, разорванную несколькими воздушными зазорами.
2. ядро имеет примерно одинаковую площадь поперечного сечения по всей длине.
3. любые воздушные зазоры между секциями материала сердцевины не велики по сравнению с размерами поперечного сечения сердцевины.
4. поток утечки пренебрежимо мал.

Магнитное поле в магнитной цепи

Магнитное поле, создаваемое электромагнитом, пропорционально N и I , поэтому этому продукту NI присвоено название магнитодвижущей силы . Для электромагнита с одной магнитной цепью закон Ампера сводится к:

$NI=H_{\mathrm {core} }L_{\mathrm {core} }+H_{\mathrm {gap} }L_{\mathrm {gap} }$

$NI=B\left({\frac {L_{\mathrm {core} }}{\mu }}+{\frac {L_{\mathrm {gap} }}{\mu _{0}}}\right)$ ( 2 )

Это нелинейное уравнение поскольку µ меняется в зависимости от B. , Для точного решения значение μ при используемом значении B материала сердцевины должно быть получено из кривой гистерезиса . Если B неизвестен, уравнение необходимо решать численными методами .

Более того, если магнитодвижущая сила значительно превышает насыщение, то есть материал сердечника находится в состоянии насыщения, магнитное поле будет примерно равно значению насыщения B _sat для материала и не будет сильно меняться при изменении NI . Для замкнутой магнитной цепи (без воздушного зазора) большинство материалов сердечника насыщаются при магнитодвижущей силе примерно 800 ампер-витков на метр пути магнитного потока.

Для большинства основных материалов $\mu _{r}\approx 2000{\text{–}}6000\,$. Таким образом, в приведенном выше уравнении (2) доминирует второй член. Поэтому в магнитопроводах с воздушным зазором B сильно зависит от длины воздушного зазора, а длина пути потока в сердечнике не имеет большого значения. Учитывая воздушный зазор в 1 мм, для создания магнитного поля силой 1 Тл требуется магнитодвижущая сила около 796 Ампер-витков.

Замкнутая магнитная цепь

Поперечное сечение подъемного электромагнита, как на фотографии выше, демонстрирует цилиндрическую конструкцию. Обмотки ( С ) представляют собой плоские медные полосы, выдерживающие силу Лоренца магнитного поля. Сердечник образован толстым железным корпусом ( D ), охватывающим обмотки.

Для замкнутой магнитной цепи (без воздушного зазора), например, в электромагните, поднимающем кусок железа, перекинутый через его полюса, уравнение ( 2 ) принимает вид:

$B={\frac {NI\mu }{L}}$ ( 3 )

Подставляя в ( 1 ), сила равна:

$F={\frac {\mu ^{2}N^{2}I^{2}A}{2\mu _{0}L^{2}}}$ ( 4 )

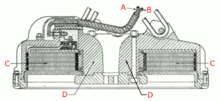
Видно, что для максимизации силы сердечник с коротким путем потока L и широкой площадью поперечного сечения A предпочтителен (это также относится к магнитам с воздушным зазором). Для этого в таких устройствах, как подъемные магниты (см. фото выше) и громкоговорители, часто используется плоская цилиндрическая конструкция. Обмотка намотана вокруг короткого широкого цилиндрического сердечника, образующего один полюс, а толстый металлический корпус, охватывающий внешнюю часть обмоток, образует другую часть магнитной цепи, перенося магнитное поле вперед, образуя другой полюс.

Сила между электромагнитами

Вышеуказанные методы применимы к электромагнитам с магнитной цепью и не применимы, когда большая часть пути магнитного поля находится вне сердечника. Неконтурным примером может служить магнит с прямым цилиндрическим сердечником, подобный тому, который показан в верхней части этой статьи. Сосредотачиваясь только на силе между двумя электромагнитами (или постоянными магнитами) с четко определенными «полюсами», где силовые линии выходят из ядра, используется специальная аналогия, называемая моделью магнитного заряда, которая предполагает, что магнитное поле создается фиктивными «магнитными зарядами». ' на поверхности полюсов. Эта модель предполагает точечные полюса вместо реально существующих поверхностей, и поэтому она дает хорошее приближение только тогда, когда расстояние между магнитами намного больше, чем их диаметр, поэтому она полезна только для силы между ними.

Силу магнитного полюса электромагнитов можно найти по формуле:

$$m={\frac {NIA}{L}}$$

Сила между двумя полюсами равна:

$$F={\frac {\mu _{0}m_{1}m_{2}}{4\pi r^{2}}}$$

Каждый электромагнит имеет два полюса, поэтому общая сила, действующая на данный магнит со стороны другого магнита, равна векторной сумме сил полюсов другого магнита, действующих на каждый полюс данного магнита.

Побочные эффекты

Электромагниты имеют ряд побочных эффектов, которые необходимо предусмотреть в их конструкции. Обычно они становятся более значимыми в более крупных электромагнитах.

Омический нагрев

Большие алюминиевые шины, передающие ток к электромагнитам в лаборатории сильного поля LNCMI (Национальная лаборатория интенсивных магнитных полей).

Единственная мощность, потребляемая электромагнитом постоянного тока в установившемся режиме, обусловлена ​​сопротивлением обмоток и рассеивается в виде тепла. Некоторые большие электромагниты требуют систем водяного охлаждения в обмотках для отвода отходящего тепла .

Поскольку магнитное поле пропорционально произведению NI , количество витков в обмотках N и ток I можно выбрать так, чтобы минимизировать тепловые потери, при условии, что их произведение будет постоянным. Поскольку рассеиваемая мощность P = I ² R , увеличивается пропорционально квадрату тока, но увеличивается только примерно линейно с количеством обмоток, мощность, теряемую в обмотках, можно минимизировать, уменьшив I и пропорционально увеличив количество витков N , или используя более толстый провод для уменьшения сопротивления. Например, уменьшение вдвое I и удвоение N вдвое уменьшает потери мощности, как и удвоение площади провода. В любом случае увеличение количества проводов снижает омические потери. По этой причине электромагниты часто имеют значительную толщину обмоток.

Однако ограничением увеличения N или снижения сопротивления является то, что обмотки занимают больше места между частями сердечника магнита. Если площадь, доступная для обмоток, заполнена, большее количество витков требует перехода на провод меньшего диаметра, имеющий более высокое сопротивление, что сводит на нет преимущество использования большего количества витков. Так вот в больших магнитах есть минимальные потери тепла, которые невозможно уменьшить. Оно увеличивается с увеличением квадрата магнитного потока B ² .

напряжения

Электромагнит обладает значительной индуктивностью и сопротивляется изменениям тока, проходящего через его обмотки. Любые резкие изменения тока обмотки вызывают большие скачки напряжения на обмотках. Это связано с тем, что когда ток через магнит увеличивается, например, когда он включен, энергия цепи должна сохраняться в магнитном поле. Когда он выключен, энергия поля возвращается в цепь.

Если для контроля тока обмотки использовать обычный переключатель , это может привести к образованию искр на выводах переключателя. Этого не происходит при включении магнита, поскольку ограниченное напряжение питания приводит к медленному увеличению тока через магнит и энергии поля, но при его выключении энергия магнитного поля внезапно возвращается в цепь, вызывая большой скачок напряжения и дугу на контактах переключателя, что может привести к их повреждению. В небольших электромагнитах между контактами иногда используется конденсатор , который уменьшает искрение за счет временного сохранения тока. Чаще всего диод используется для предотвращения скачков напряжения, обеспечивая путь рециркуляции тока через обмотку до тех пор, пока энергия не рассеется в виде тепла. Диод подключен параллельно обмотке, ориентирован так, что в установившемся режиме он смещен в обратном направлении и не проводит ток. Когда напряжение питания снимается, скачок напряжения смещает диод вперед, и реактивный ток продолжает течь через обмотку, через диод и обратно в обмотку. Диод, используемый таким образом, называется Обратный диод или обратный диод .

Большие электромагниты обычно питаются от электронных источников переменного тока , управляемых микропроцессором , которые предотвращают скачки напряжения, выполняя изменения тока медленно, плавно. Для включения или выключения большого магнита может потребоваться несколько минут.

Силы Лоренца

В мощных электромагнитах магнитное поле оказывает воздействие на каждый виток обмоток за счет силы Лоренца . $q\mathbf {v} \times \mathbf {B}$ действует на движущиеся заряды внутри провода. Сила Лоренца перпендикулярна как оси провода, так и магнитному полю. Это можно представить как давление между силовыми линиями магнитного поля , раздвигающее их. Он оказывает два воздействия на обмотки электромагнита:

• Силовые линии внутри оси катушки оказывают радиальное воздействие на каждый виток обмоток, стремясь вытолкнуть их наружу во всех направлениях. Это вызывает растягивающее напряжение в проволоке.
• Линии поля рассеяния между каждым витком катушки оказывают силу притяжения между соседними витками, стремясь стянуть их вместе.

Силы Лоренца возрастают с ростом B ² . при движении при включении и выключении питания В больших электромагнитах обмотки должны быть прочно закреплены на месте, чтобы предотвратить возникновение усталости металла в обмотках . В конструкции Биттера (см. ниже), используемой в исследовательских магнитах с очень сильным полем, обмотки выполнены в виде плоских дисков, чтобы противостоять радиальным силам, и зажаты в осевом направлении, чтобы противостоять осевым силам.

потери

В электромагнитах переменного тока (AC), используемых в трансформаторах , индукторах , двигателях и генераторах переменного тока , магнитное поле постоянно меняется. Это вызывает потери энергии в их магнитных сердечниках , которые рассеиваются в виде тепла в сердечнике. Потери возникают в результате двух процессов:

• Вихревые токи . Согласно закону индукции Фарадея , изменяющееся магнитное поле индуцирует циркулирующие электрические токи внутри близлежащих проводников, называемые вихревыми токами . Энергия этих токов рассеивается в виде тепла на электрическом сопротивлении проводника, поэтому они являются причиной потерь энергии. Поскольку железный сердечник магнита является проводящим и большая часть магнитного поля сосредоточена там, основной проблемой являются вихревые токи в сердечнике. Вихревые токи представляют собой замкнутые контуры тока, которые текут в плоскостях, перпендикулярных магнитному полю. Рассеиваемая энергия пропорциональна площади, заключенной в контуре. Чтобы их предотвратить, сердечники электромагнитов переменного тока изготавливают из стопок тонких стальных листов или пластин , ориентированных параллельно магнитному полю, с изолирующим покрытием на поверхности. Слои изоляции предотвращают протекание вихревых токов между листами. Любые оставшиеся вихревые токи должны течь в поперечном сечении каждой отдельной пластины, что значительно снижает потери. Другой альтернативой является использование ферритовый сердечник , который является непроводником.
• Гистерезисные потери : изменение направления намагничивания магнитных доменов в материале сердечника в каждом цикле приводит к потере энергии из-за коэрцитивной силы материала. Эти потери называются гистерезисом . Потеря энергии за цикл пропорциональна площади петли гистерезиса на графике BH . Чтобы минимизировать эти потери, магнитные сердечники, используемые в трансформаторах и других электромагнитах переменного тока, изготавливаются из «мягких» материалов с низкой коэрцитивной силой, таких как кремниевая сталь или мягкий феррит . Потери энергии за цикл переменного тока постоянны для каждого из этих процессов, поэтому потери мощности линейно возрастают с частотой .

Электромагниты сильного поля

Сверхпроводящие электромагниты

Самый мощный электромагнит в мире, гибридный сверхпроводящий магнит Биттера на 45 Тл в Национальной лаборатории сильных магнитных полей США, Таллахасси, Флорида, США.

Основная статья: Сверхпроводящий магнит

Когда необходимо магнитное поле выше ферромагнитного предела в 1,6 Тл, сверхпроводящие электромагниты можно использовать . Вместо использования ферромагнитных материалов в них используются сверхпроводящие обмотки, охлаждаемые жидким гелием , которые проводят ток без электрического сопротивления . Они позволяют течь огромным токам, которые генерируют интенсивные магнитные поля. Сверхпроводящие магниты ограничены силой поля, при которой материал обмотки перестает быть сверхпроводящим. Текущие конструкции ограничены 10–20 Тл, при этом текущий (2017 г.) рекорд составляет 32 Тл. Необходимое холодильное оборудование и криостат делают их значительно дороже обычных электромагнитов. Однако в приложениях с высокой мощностью это можно компенсировать более низкими эксплуатационными расходами, поскольку после запуска для обмоток не требуется питание, поскольку энергия не теряется на омический нагрев. Они используются в ускорителях частиц и аппаратах МРТ .

Горькие электромагниты

Основная статья: Горький электромагнит

И электромагниты с железным сердечником, и сверхпроводящие электромагниты имеют пределы поля, которое они могут создавать. Таким образом, самые мощные искусственные магнитные поля были созданы несверхпроводящими электромагнитами с воздушным сердечником , конструкция которых была изобретена Фрэнсисом Биттером в 1933 году и названа электромагнитами Биттера . Вместо проволочных обмоток магнит Биттера состоит из соленоида, состоящего из стопки проводящих дисков, расположенных так, что ток движется через них по спирали, с отверстием в центре, где создается максимальное поле. Эта конструкция обладает механической прочностью, позволяющей противостоять экстремальным силам Лоренца поля, которые возрастают с увеличением B. ² . Диски пронизаны отверстиями, через которые проходит охлаждающая вода, отводящая тепло, вызванное сильным током. Самое сильное непрерывное поле, достигнутое исключительно с помощью резистивного магнита, по состоянию на 22 августа 2017 г. составляло 41,5 Тесла. , произведенный электромагнитом Биттера в Национальной лаборатории сильных магнитных полей в Таллахасси , Флорида . Предыдущий рекорд составлял 37,5 т. Самое сильное непрерывное магнитное поле в целом, 45 Тл, был достигнут в июне 2000 года с помощью гибридного устройства, состоящего из магнита Биттера внутри сверхпроводящего магнита.

Фактором, ограничивающим силу электромагнитов, является неспособность рассеивать огромное количество отходящего тепла, поэтому более мощные поля, до 100 Тл, были получены из резистивных магнитов путем пропускания через них коротких импульсов сильного тока; период неактивности после каждого импульса позволяет удалить тепло, выделяемое во время импульса, перед следующим импульсом.

Сжатие потока со взрывной накачкой

Основная статья: Генератор сжатия потока со взрывной накачкой

Генератор сжатия потока со взрывной накачкой представляет собой полую трубку. Полая медная трубка действует как одновитковая вторичная обмотка трансформатора; когда импульс тока от конденсатора в обмотках создает импульс магнитного поля, это создает сильный окружной ток в трубке, захватывая линии магнитного поля внутри. Затем взрывчатка разрушает трубку, уменьшая ее диаметр, а силовые линии сближаются, увеличивая поле.

Самые мощные искусственные магнитные поля были созданы с помощью взрывчатки для сжатия магнитного поля внутри электромагнита при его пульсации; их называют генераторами сжатия потока со взрывной накачкой . Имплозия . сжимает магнитное поле до значений около 1000 Тл на несколько микросекунд. Хотя этот метод может показаться очень разрушительным, формирование заряда перенаправляет взрыв наружу, чтобы свести к минимуму вред для эксперимента. Эти устройства известны как разрушающие импульсные электромагниты. Они используются в исследованиях в области физики и материаловедения для изучения свойств материалов в сильных магнитных полях.

Определение терминов

Срок	Значение	Единица
$A\,$	площадь поперечного сечения сердечника	квадратный метр
$B\,$	Магнитное поле (Плотность магнитного потока)	Тесла
$F\,$	Сила, действующая магнитным полем	Ньютон
$H\,$	Намагничивающее поле	ампер на метр
$I\,$	Ток в обмоточном проводе	ампер
$L\,$	Общая длина пути магнитного поля $L_{\mathrm {core} }+L_{\mathrm {gap} }\,$	метр
$L_{\mathrm {core} }\,$	Длина пути магнитного поля в материале сердечника	метр
$L_{\mathrm {gap} }\,$	Длина пути магнитного поля в воздушных зазорах	метр
$m_{1},m_{2}\,$	Сила полюса электромагнита	амперметр
$\mu \,$	Проницаемость материала сердечника электромагнита	Ньютон на квадратный ампер
$\mu _{0}\,$	Проницаемость свободного пространства (или воздуха) = $4\pi (10^{-7})\ \mathrm {N} \cdot \mathrm {A} ^{-2}$	Ньютон на квадратный ампер
$\mu _{r}\,$	Относительная проницаемость материала сердечника электромагнита	безразмерный
$N\,$	Число витков провода на электромагните	безразмерный
$r\,$	Расстояние между полюсами двух электромагнитов	метр

См. также

• Дипольный магнит – самая простая форма магнита.
• Электромагнетизм
• Электропостоянный магнит - устройство магнитотвердых электромагнитов.
• Катушка возбуждения
• Магнитный подшипник
• Магнит импульсного поля
• Квадрупольный магнит - комбинация магнитов и электромагнитов, используемая в основном для воздействия на движение заряженных частиц.

Внешние ссылки

• Электромагниты - Фейнмановские лекции по физике